2018年高中数学北师大版必修2课件:第二章解析几何初步2-1-1直线的倾斜角和斜率课件(22张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第二章解析几何初步2-1-1直线的倾斜角和斜率课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 812.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-15 00:00:00 | ||
图片预览






文档简介
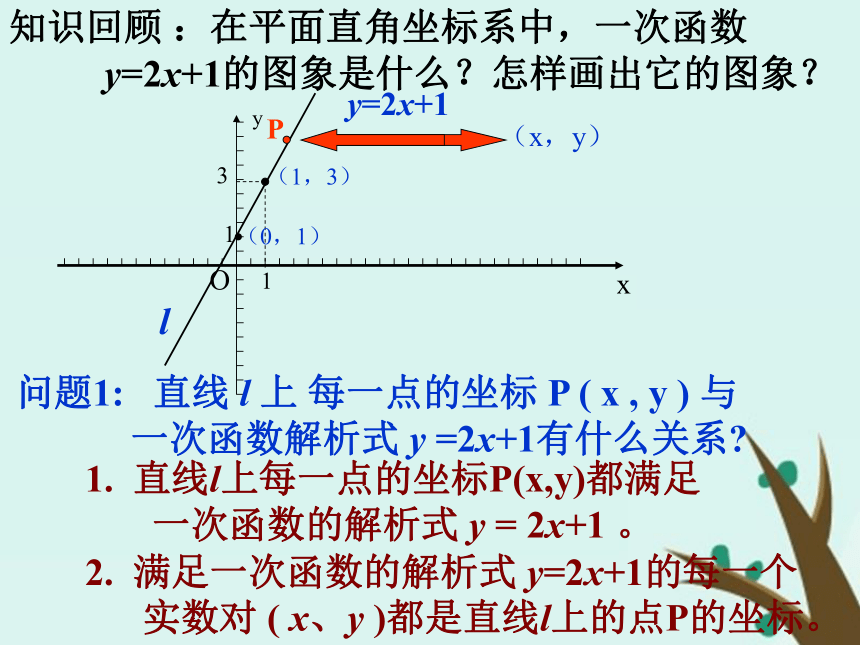
课件22张PPT。直 线 的 倾 斜 角 和 斜 率y=2x+1 2. 满足一次函数的解析式 y=2x+1的每一个
实数对 ( x、y )都是直线l上的点P的坐标。 1. 直线l上每一点的坐标P(x,y)都满足
一次函数的解析式 y = 2x+1 。知识回顾 :在平面直角坐标系中,一次函数 y=2x+1的图象是什么?怎样画出它的图象?(x,y)问题1: 直线 l 上 每一点的坐标 P ( x , y ) 与
一次函数解析式 y =2x+1有什么关系? l问题2: 平面直角坐标系中的所有直线l 都是
一次函数的图象吗?思考1:上图中的直线l是一次函数的图象吗? 思考2:怎样用更 一般的方法表示平面直角坐标系 中的直线 l ? 2. 二元一次方程 2x- y +1 =0的解
所对应的点P(x,y)都在直线l上 。 1. 直线l上每一点的坐标P(x,y)都是
二元一次方程 2x- y +1 =0的解。 问题3:将一次函数解析式 y =2x+1改写成
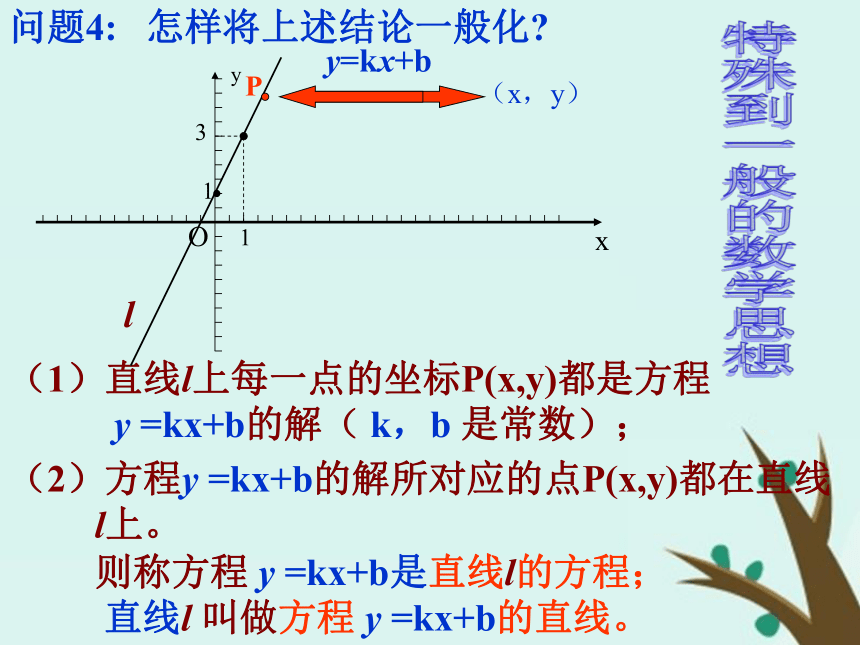
2x- y+1=0,问题1的两个结论应该怎样说? l(2)方程y =kx+b的解所对应的点P(x,y)都在直线
l上。(1)直线l上每一点的坐标P(x,y)都是方程
y =kx+b的解( k,b 是常数);问题4: 怎样将上述结论一般化? 则称方程 y =kx+b是直线l的方程;
直线l 叫做方程 y =kx+b的直线。 特殊到一般的数学思想 以一个方程的解为坐标的点都是某条直线上的
点,反过来,这条直线上的点的坐标都满足这个
方程的解,这时,这个方程就叫做这条直线的方程,
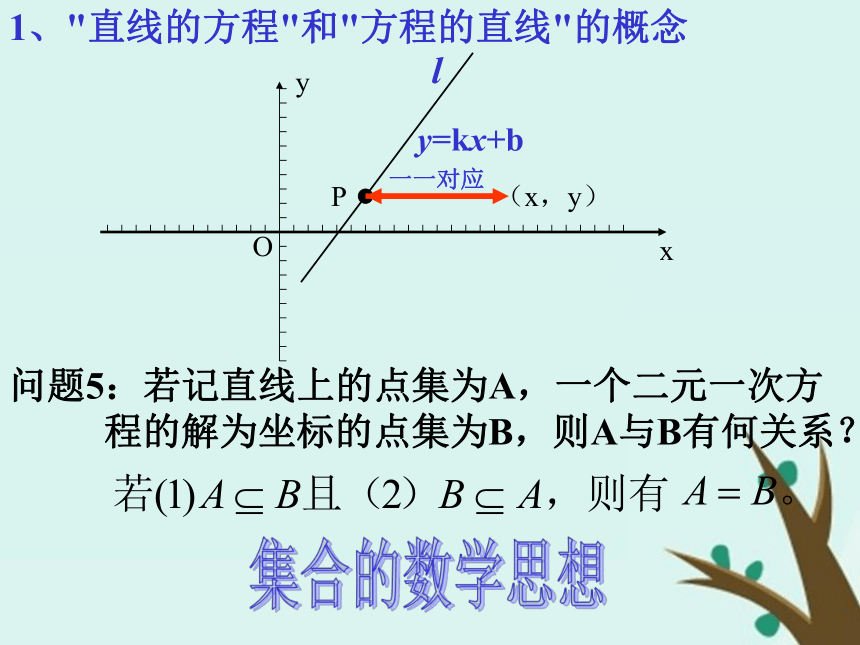
这条直线叫做这个方程的直线. y=kx+b(x,y)1、"直线的方程"和"方程的直线"的概念 一一对应y=kx+b(x,y)1、"直线的方程"和"方程的直线"的概念 一一对应问题5:若记直线上的点集为A,一个二元一次方
程的解为坐标的点集为B,则A与B有何关系?集合的数学思想l问题6:在平面直角坐标系中研究直线时,
就是利用直线与方程的这种关系,
建立直线方程的概念和定义,
并通过方程来研究直线的有关问题.
为此,我们先研究直线的方程 y =kx+b.用代数的方法来研究几何问题问题7:如何研究直线的方程 y =kx+b.
( k,b 是常数)数学实验:(1)当b=0时,y=kx,则 k=y/x=tanθ分类讨论的数学思想问题8:直线的倾斜角与斜率如何定义?直线倾斜角的范围是:3。直线的斜率k=tanθ (当倾斜角不是 900)X.pYOX.pYOX.pYOX.pYO(1)(2)(4)(3)oo例1。标出下列图中直线的倾斜角,并说出各自斜率符号?
k>0k<0k不存在K=04.直线的倾斜角与斜率之间的关系: k=0 无k>0递增不存在
无k<0递增例2。判断正误: ③因为所有直线都有倾斜角,所以所有直线都有
斜率。 ( ) ④因为平行于y轴的直线的斜率不存在,所以平
行于y轴的直线的倾斜角不存在 ( )XXXX已知两点p1(x1,y1),p2(x2,y2),(x1≠x2)则由p1,p2确定的直线的斜率为k=?问题9:经过两点的直线确定吗?(1)向量 的方向是向上的. XYO(1)XYO(2)而且直线OP的倾斜角也是α. (2)向量 的方向是向上的. XYO(1)XYO(2)请同学们自己验证。思考:是否还有其它方法来证明斜率公式?例3。求经过点A(-2,0),B(-5,3)两点的直线的斜
率和倾斜角。即 即直线的斜率为-1,倾斜角为解:例4。 已知直线 和 的斜率分别是 和 ,求
它们的倾斜角及确定两条直线的位置关系。由图可知
解:例4。 已知直线 和 的斜率分别是 和 ,求
它们的倾斜角及确定两条直线的位置关系。练习1。 已知a,b,c是两两不等的实数,求经过下列每两个点的直线的倾斜角与斜率。(1)A(a,c),B(b,c)
(2)C(a,b),D(a,c)
(3)P(b,b+c),Q(a,c+a)4。课堂练习小结:1。正确理解直线方程与方程的直线概念 2。小结:1。正确理解直线方程与方程的直线概念 2。
实数对 ( x、y )都是直线l上的点P的坐标。 1. 直线l上每一点的坐标P(x,y)都满足
一次函数的解析式 y = 2x+1 。知识回顾 :在平面直角坐标系中,一次函数 y=2x+1的图象是什么?怎样画出它的图象?(x,y)问题1: 直线 l 上 每一点的坐标 P ( x , y ) 与
一次函数解析式 y =2x+1有什么关系? l问题2: 平面直角坐标系中的所有直线l 都是
一次函数的图象吗?思考1:上图中的直线l是一次函数的图象吗? 思考2:怎样用更 一般的方法表示平面直角坐标系 中的直线 l ? 2. 二元一次方程 2x- y +1 =0的解
所对应的点P(x,y)都在直线l上 。 1. 直线l上每一点的坐标P(x,y)都是
二元一次方程 2x- y +1 =0的解。 问题3:将一次函数解析式 y =2x+1改写成
2x- y+1=0,问题1的两个结论应该怎样说? l(2)方程y =kx+b的解所对应的点P(x,y)都在直线
l上。(1)直线l上每一点的坐标P(x,y)都是方程
y =kx+b的解( k,b 是常数);问题4: 怎样将上述结论一般化? 则称方程 y =kx+b是直线l的方程;
直线l 叫做方程 y =kx+b的直线。 特殊到一般的数学思想 以一个方程的解为坐标的点都是某条直线上的
点,反过来,这条直线上的点的坐标都满足这个
方程的解,这时,这个方程就叫做这条直线的方程,
这条直线叫做这个方程的直线. y=kx+b(x,y)1、"直线的方程"和"方程的直线"的概念 一一对应y=kx+b(x,y)1、"直线的方程"和"方程的直线"的概念 一一对应问题5:若记直线上的点集为A,一个二元一次方
程的解为坐标的点集为B,则A与B有何关系?集合的数学思想l问题6:在平面直角坐标系中研究直线时,
就是利用直线与方程的这种关系,
建立直线方程的概念和定义,
并通过方程来研究直线的有关问题.
为此,我们先研究直线的方程 y =kx+b.用代数的方法来研究几何问题问题7:如何研究直线的方程 y =kx+b.
( k,b 是常数)数学实验:(1)当b=0时,y=kx,则 k=y/x=tanθ分类讨论的数学思想问题8:直线的倾斜角与斜率如何定义?直线倾斜角的范围是:3。直线的斜率k=tanθ (当倾斜角不是 900)X.pYOX.pYOX.pYOX.pYO(1)(2)(4)(3)oo例1。标出下列图中直线的倾斜角,并说出各自斜率符号?
k>0k<0k不存在K=04.直线的倾斜角与斜率之间的关系: k=0 无k>0递增不存在
无k<0递增例2。判断正误: ③因为所有直线都有倾斜角,所以所有直线都有
斜率。 ( ) ④因为平行于y轴的直线的斜率不存在,所以平
行于y轴的直线的倾斜角不存在 ( )XXXX已知两点p1(x1,y1),p2(x2,y2),(x1≠x2)则由p1,p2确定的直线的斜率为k=?问题9:经过两点的直线确定吗?(1)向量 的方向是向上的. XYO(1)XYO(2)而且直线OP的倾斜角也是α. (2)向量 的方向是向上的. XYO(1)XYO(2)请同学们自己验证。思考:是否还有其它方法来证明斜率公式?例3。求经过点A(-2,0),B(-5,3)两点的直线的斜
率和倾斜角。即 即直线的斜率为-1,倾斜角为解:例4。 已知直线 和 的斜率分别是 和 ,求
它们的倾斜角及确定两条直线的位置关系。由图可知
解:例4。 已知直线 和 的斜率分别是 和 ,求
它们的倾斜角及确定两条直线的位置关系。练习1。 已知a,b,c是两两不等的实数,求经过下列每两个点的直线的倾斜角与斜率。(1)A(a,c),B(b,c)
(2)C(a,b),D(a,c)
(3)P(b,b+c),Q(a,c+a)4。课堂练习小结:1。正确理解直线方程与方程的直线概念 2。小结:1。正确理解直线方程与方程的直线概念 2。
