2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-1平行关系的判定课件(44张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-1平行关系的判定课件(44张) |

|
|
| 格式 | zip | ||
| 文件大小 | 554.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-15 20:37:38 | ||
图片预览









文档简介
课件44张PPT。平行关系的判定在空间中直线与平面有几种位置关系?1、直线在平面内2、直线与平面相交3、直线与平面平行一、知识回顾:文字语言图形语言符号语言 怎样判定直线与平面平行呢?问题二、引入新课 根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.但是,直线无限延长,平面无限延展,如何保证直线与平面没有公共点呢? 在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.(1)分析实例—猜想定理三、线面平行判定定理的探究将课本的一边AB紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行?ABCDCD是桌面外一条直线, AB是桌面内一条直线, CD ∥ AB ,则CD ∥桌面猜想:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。(2)做一做(3)猜一猜直线和平面平行的判定定理 如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。b??a∥ ba ??a ∥ ?四、规律总结:1、定理三个条件缺一不可。注明:五、讨论定理中的条件缺失的情况:
判断下列命题是否正确,若不正确,请用图形语言或模型加以表达
(1)
(2)
(3)五、讨论定理中的条件缺失的情况:
判断下列命题是否正确,若不正确,请用图形语言或模型加以表达
(1)
(2)
(3)(1)、定理三个条件缺一不可注:(2)该定理作用:“线线平行?线面平行”——空间问题“平面化”
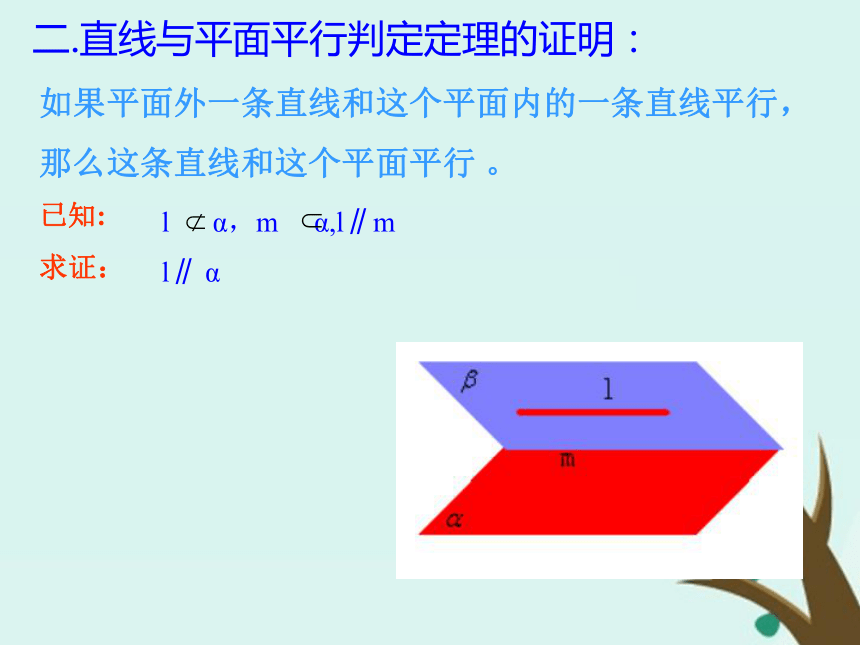
(3)定理告诉我们:要证线面平行,只要在面?内找一条线,与已知直线a平行。二.直线与平面平行判定定理的证明:如果平面外一条直线和这个平面内的一条直线平行,
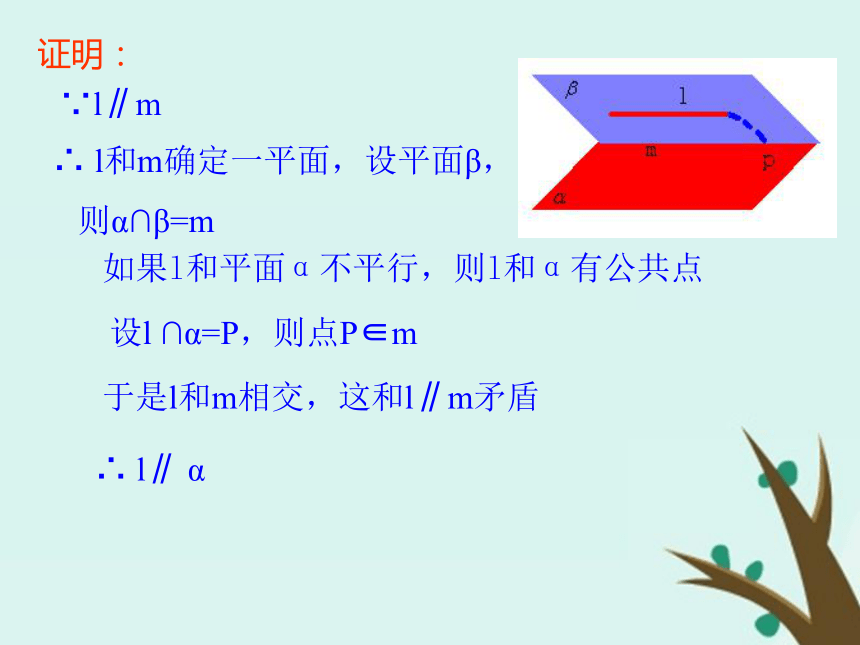
那么这条直线和这个平面平行 。l α,m α,l∥ml∥ α已知:求证:证明:∵l∥m∴ l和m确定一平面,设平面β,
则α∩β=m如果l和平面α不平行,则l和α有公共点设l ∩α=P,则点P∈m于是l和m相交,这和l∥m矛盾∴ l∥ α六、理论提升
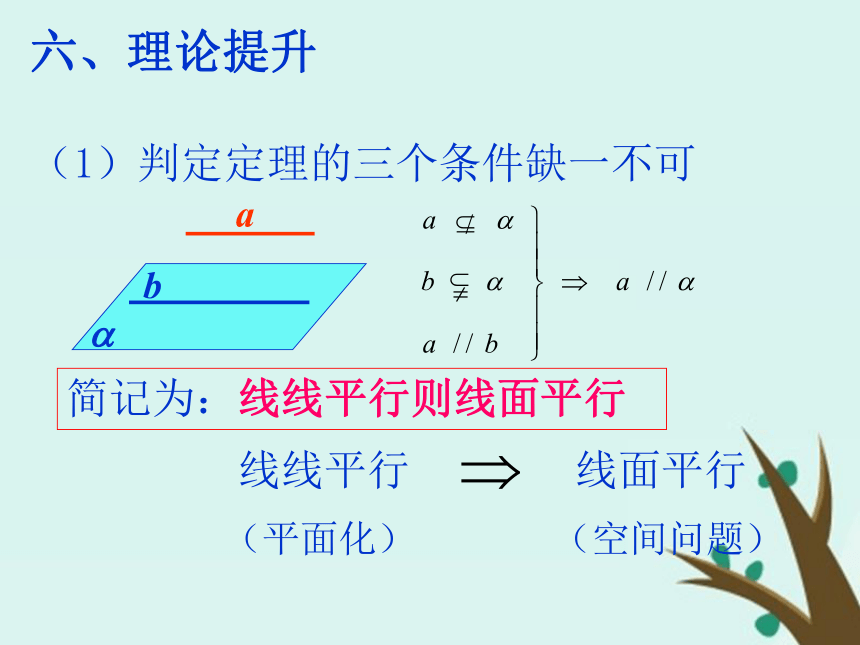
(1)判定定理的三个条件缺一不可简记为:线线平行则线面平行(平面化) (空间问题)(2)实践:(口答)
如图:长方体ABCD—A′B′C′D′六个表面中,
① 与AB平行的平面是 ____________
② 与AA′平行的平面是 _____________
③ 与AD平行的平面是 ______________平面A′B′C′D′和平面DCC′D′平面BCC′ B′和平面DCC′D′平面A′B′C′D′和平面BCC′B′判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.
( 1 )如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;( )(2)如果直线a和平面α 满足a∥ α ,那么a 与α内的任何直线平行;( )(3)如果直线a、b和平面α 满足a ∥ α,b ∥ α,那么a ∥ b ;( )( 4 )过平面外一点和这个平面平行的直线只有一条.( )试一试(5)若直线a平行于平面 内的无数条直线,则
(?)
七、典例精析:例1 已知:空间四边形ABCD中,E、F分别 是AB、AD的中点。
求证:EF ∥ 平面BCD
分析:EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢?连结BD立刻就清楚了。例1 已知:空间四边形ABCD中,E,F分别是
AB,AD的中点.
求证:EF//平面BCD.证明:连接BD.因为AE=EB,AF=FD,
所以EF//BD(三角形中位线定理)小结:在平面内找(作)一条直线与平面外的直线平行时可以通过
三角形的中位线、梯形的中位线、平行线的性质等来完成。八、变式强化:如图,在空间四面体中,E、F、M、N分别为棱AB、AD、DC、BC的中点
【变式一】
(1)四边形EFMN , 是什么四边形?平行四边行【变式二】
(2)直线AC与平面EFMN的位置关系是什么?为什么?AC与平面EFMN平行【变式三】
(3)在这图中,你能找出哪些线面平行关系? ①直线BD与平面EFMN②直线AC与平面EFMN③直线EF与平面BCD④直线FM与平面ABC⑤直线MN与平面ABD⑥直线EN与平面ACD九、演练反馈判断下列命题是否正确:(1)一条直线平行于一个平面, 这条直线就与这个平面内的任意直线平行。
(2)直线在平面外是指直线和平面最多有一个公共点.
(3)过平面外一点有且只有一条直线与已知平面平行。
(4)若直线 平行于平面 内的无数条直线,则
(5)如果a、b是两条直线,且 ,那么a平行于经过b的任何平面.
?
(?)(?)(?)(?)(?)证明:连接BD交AC于点O,连接OE,随堂练习 两个全等的正方形ABCD、ABEF不在同
一平面内,M、N是对角线AC、BF的中点
求证:MN ∥面BCE练一练PQ引申: M、N 是AC,BF上的点且AM=FN,求证:MN ∥面BCE
关键:在平面内找(作)一条直线与平面外的直线平行,在寻找平行直线时可以通过三角形的中位线、梯形的中位线、平行线的性质等来完成。
十、总结提炼1.证明直线与平面平行的方法:(1)利用定义;(2)利用判定定理.直线与平面没有公共点2.数学思想方法:转化的思想假设直线a不平行于平面α,则a ∩ α = P。定理:如果不在平面内的一条直线 和平面内的
一条直线平行,那么这条直线 和这个平面平行.证明:(用反证法)课外阅读已知:P是平行四边形ABCD所在平面外一点,M为PB的中点.求证:PD//平面MAC.O试一试2。已知E、F分别为正方体ABCD-A1B1C1D1棱BC、C1D1的中点,求证:EF ∥平面BB1D1 D.D 取BD中点O,则OE为△ BDC 的中位线.∴D1OEF为平行四边形∴EF ∥D1O∴ EF ∥平面BB1DD1 EFO证明:平面与平面平行的判定(1)平行(2)相交1.?平面与平面有几种位置关系?没有公共点有一条公共直线复习引入①问1:两个平面平行,那么其中一个平面的直线与另一个平面的位置关系如何?平行②问2:如果一个平面内的所有直线,都与另一个平面平行,那么这两个平面的位置关系如何?平行结论:两个平面平行的问题可以转化为一个平面内的直线与另一个平面平行的问题.③当然我们不需要证明所有直线都与另一平面平行,那么需要几条直线才能说明问题呢?复习引入2.问题:还可以怎样判定平面与平面平行呢?(两平面平行)(两平面相交)探究(两平面平行)(两平面相交)EF直线的条数不是关键!探究直线相交才是关键!探究线不在多,重在相交!2.平面与平面平行的判定定理若一个平面内两条相交直线分别平行于另一个平面, 则这两个平面平行.(1)该定理中,“两条”,“相交”都是必要条件,缺一不可: (2)该定理作用:“线面平行?面面平行”(3)应用该定理,关键是在一平面内找到两条相交直线分别与另一平面内两条直线平行即可.线线平行?线面平行?面面平行练习×××××证明:因为ABCD-A1B1C1D1为正方体,
所以D1C1∥A1B1,D1C1=A1B1
又AB∥A1B1,AB=A1B1,
∴D1C1∥AB,D1C1=AB,
∴D1C1BA是平行四边形,
∴D1A∥C1B,由直线与平面平行的判定,可知同理??D1B1∥平面C1BD.
又 D1A∩D1B1=D1,所以,平面AB1D1∥平面C1BD.D1A∥平面C1BD,平行四边形对边平行是常用的找平行线的方法.拓展:如果一个平面内有两条相交直线与另一个平面内的两条相交直线分别平行,那么这两个平面平行练2: 正方体ABCD-A1B1C1D1中,若M、N、P、Q分别是棱A1D1,A1B1,BC,CD的中点,求证:平面AMN//平面C1QP.练1: 正方体ABCD-A1B1C1D1中,若M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN//平面EFDB.K变式练习C1ACB1BMNA1F证明:取A1C1中点F,连结NF,FC.∵N为A1B1中点,M是BC的中点,∴NFCM为平行四边形,故MN∥CF∴ MN∥平面AA1C1C.例 如图,三棱柱ABC-A1B1C1中,M、 N分别是BC和A1B1的中点,求证:MN∥平面AA1C1C练习练1:三棱柱ABC-A1B1C1中,E是AC1上的点,F是CB1上的中点,求证:A1B//平面ADC1 .G同理可证GF//平面ABC.又GE∩GF=G,所以面GEF//面ABC.例 如图,四棱锥P-ABCD中,底面ABCD是正方形,M,N分别是AB,PC的中点,求证:MN//平面PAD.HG法二:取DC的中点G,连接GN,GM ,往证面GMN//面PAD即可.练:如图,四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,E,F分别是PC,BD的中点,求证:EF//平面PAD.GH练习例 如图,点B为△ACD所在平面外一点,M,N分别为△ABC,△ABD的重心. (1)求证:MN//平面ACD. (2)若底面边长为1为正三角形,求线段的MN的长度.EF线段成比例也是常用的找平行线的方法.小结1.两个平面平行:(1)定义:(2)判定定理:2.数学思想方法:转化的思想空间问题平面问题平面和平面没有公共点线线平行面面平行线面平行转化转化转化
判断下列命题是否正确,若不正确,请用图形语言或模型加以表达
(1)
(2)
(3)五、讨论定理中的条件缺失的情况:
判断下列命题是否正确,若不正确,请用图形语言或模型加以表达
(1)
(2)
(3)(1)、定理三个条件缺一不可注:(2)该定理作用:“线线平行?线面平行”——空间问题“平面化”
(3)定理告诉我们:要证线面平行,只要在面?内找一条线,与已知直线a平行。二.直线与平面平行判定定理的证明:如果平面外一条直线和这个平面内的一条直线平行,
那么这条直线和这个平面平行 。l α,m α,l∥ml∥ α已知:求证:证明:∵l∥m∴ l和m确定一平面,设平面β,
则α∩β=m如果l和平面α不平行,则l和α有公共点设l ∩α=P,则点P∈m于是l和m相交,这和l∥m矛盾∴ l∥ α六、理论提升
(1)判定定理的三个条件缺一不可简记为:线线平行则线面平行(平面化) (空间问题)(2)实践:(口答)
如图:长方体ABCD—A′B′C′D′六个表面中,
① 与AB平行的平面是 ____________
② 与AA′平行的平面是 _____________
③ 与AD平行的平面是 ______________平面A′B′C′D′和平面DCC′D′平面BCC′ B′和平面DCC′D′平面A′B′C′D′和平面BCC′B′判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例.
( 1 )如果a、b是两条直线,且a∥b,那么a 平行于经过b的任何平面;( )(2)如果直线a和平面α 满足a∥ α ,那么a 与α内的任何直线平行;( )(3)如果直线a、b和平面α 满足a ∥ α,b ∥ α,那么a ∥ b ;( )( 4 )过平面外一点和这个平面平行的直线只有一条.( )试一试(5)若直线a平行于平面 内的无数条直线,则
(?)
七、典例精析:例1 已知:空间四边形ABCD中,E、F分别 是AB、AD的中点。
求证:EF ∥ 平面BCD
分析:EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢?连结BD立刻就清楚了。例1 已知:空间四边形ABCD中,E,F分别是
AB,AD的中点.
求证:EF//平面BCD.证明:连接BD.因为AE=EB,AF=FD,
所以EF//BD(三角形中位线定理)小结:在平面内找(作)一条直线与平面外的直线平行时可以通过
三角形的中位线、梯形的中位线、平行线的性质等来完成。八、变式强化:如图,在空间四面体中,E、F、M、N分别为棱AB、AD、DC、BC的中点
【变式一】
(1)四边形EFMN , 是什么四边形?平行四边行【变式二】
(2)直线AC与平面EFMN的位置关系是什么?为什么?AC与平面EFMN平行【变式三】
(3)在这图中,你能找出哪些线面平行关系? ①直线BD与平面EFMN②直线AC与平面EFMN③直线EF与平面BCD④直线FM与平面ABC⑤直线MN与平面ABD⑥直线EN与平面ACD九、演练反馈判断下列命题是否正确:(1)一条直线平行于一个平面, 这条直线就与这个平面内的任意直线平行。
(2)直线在平面外是指直线和平面最多有一个公共点.
(3)过平面外一点有且只有一条直线与已知平面平行。
(4)若直线 平行于平面 内的无数条直线,则
(5)如果a、b是两条直线,且 ,那么a平行于经过b的任何平面.
?
(?)(?)(?)(?)(?)证明:连接BD交AC于点O,连接OE,随堂练习 两个全等的正方形ABCD、ABEF不在同
一平面内,M、N是对角线AC、BF的中点
求证:MN ∥面BCE练一练PQ引申: M、N 是AC,BF上的点且AM=FN,求证:MN ∥面BCE
关键:在平面内找(作)一条直线与平面外的直线平行,在寻找平行直线时可以通过三角形的中位线、梯形的中位线、平行线的性质等来完成。
十、总结提炼1.证明直线与平面平行的方法:(1)利用定义;(2)利用判定定理.直线与平面没有公共点2.数学思想方法:转化的思想假设直线a不平行于平面α,则a ∩ α = P。定理:如果不在平面内的一条直线 和平面内的
一条直线平行,那么这条直线 和这个平面平行.证明:(用反证法)课外阅读已知:P是平行四边形ABCD所在平面外一点,M为PB的中点.求证:PD//平面MAC.O试一试2。已知E、F分别为正方体ABCD-A1B1C1D1棱BC、C1D1的中点,求证:EF ∥平面BB1D1 D.D 取BD中点O,则OE为△ BDC 的中位线.∴D1OEF为平行四边形∴EF ∥D1O∴ EF ∥平面BB1DD1 EFO证明:平面与平面平行的判定(1)平行(2)相交1.?平面与平面有几种位置关系?没有公共点有一条公共直线复习引入①问1:两个平面平行,那么其中一个平面的直线与另一个平面的位置关系如何?平行②问2:如果一个平面内的所有直线,都与另一个平面平行,那么这两个平面的位置关系如何?平行结论:两个平面平行的问题可以转化为一个平面内的直线与另一个平面平行的问题.③当然我们不需要证明所有直线都与另一平面平行,那么需要几条直线才能说明问题呢?复习引入2.问题:还可以怎样判定平面与平面平行呢?(两平面平行)(两平面相交)探究(两平面平行)(两平面相交)EF直线的条数不是关键!探究直线相交才是关键!探究线不在多,重在相交!2.平面与平面平行的判定定理若一个平面内两条相交直线分别平行于另一个平面, 则这两个平面平行.(1)该定理中,“两条”,“相交”都是必要条件,缺一不可: (2)该定理作用:“线面平行?面面平行”(3)应用该定理,关键是在一平面内找到两条相交直线分别与另一平面内两条直线平行即可.线线平行?线面平行?面面平行练习×××××证明:因为ABCD-A1B1C1D1为正方体,
所以D1C1∥A1B1,D1C1=A1B1
又AB∥A1B1,AB=A1B1,
∴D1C1∥AB,D1C1=AB,
∴D1C1BA是平行四边形,
∴D1A∥C1B,由直线与平面平行的判定,可知同理??D1B1∥平面C1BD.
又 D1A∩D1B1=D1,所以,平面AB1D1∥平面C1BD.D1A∥平面C1BD,平行四边形对边平行是常用的找平行线的方法.拓展:如果一个平面内有两条相交直线与另一个平面内的两条相交直线分别平行,那么这两个平面平行练2: 正方体ABCD-A1B1C1D1中,若M、N、P、Q分别是棱A1D1,A1B1,BC,CD的中点,求证:平面AMN//平面C1QP.练1: 正方体ABCD-A1B1C1D1中,若M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN//平面EFDB.K变式练习C1ACB1BMNA1F证明:取A1C1中点F,连结NF,FC.∵N为A1B1中点,M是BC的中点,∴NFCM为平行四边形,故MN∥CF∴ MN∥平面AA1C1C.例 如图,三棱柱ABC-A1B1C1中,M、 N分别是BC和A1B1的中点,求证:MN∥平面AA1C1C练习练1:三棱柱ABC-A1B1C1中,E是AC1上的点,F是CB1上的中点,求证:A1B//平面ADC1 .G同理可证GF//平面ABC.又GE∩GF=G,所以面GEF//面ABC.例 如图,四棱锥P-ABCD中,底面ABCD是正方形,M,N分别是AB,PC的中点,求证:MN//平面PAD.HG法二:取DC的中点G,连接GN,GM ,往证面GMN//面PAD即可.练:如图,四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,E,F分别是PC,BD的中点,求证:EF//平面PAD.GH练习例 如图,点B为△ACD所在平面外一点,M,N分别为△ABC,△ABD的重心. (1)求证:MN//平面ACD. (2)若底面边长为1为正三角形,求线段的MN的长度.EF线段成比例也是常用的找平行线的方法.小结1.两个平面平行:(1)定义:(2)判定定理:2.数学思想方法:转化的思想空间问题平面问题平面和平面没有公共点线线平行面面平行线面平行转化转化转化
