2018年高中数学北师大版必修2课件:第一章立体几何初步1-6-2垂直关系的性质课件(22张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-6-2垂直关系的性质课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 484.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-15 20:39:53 | ||
图片预览




文档简介
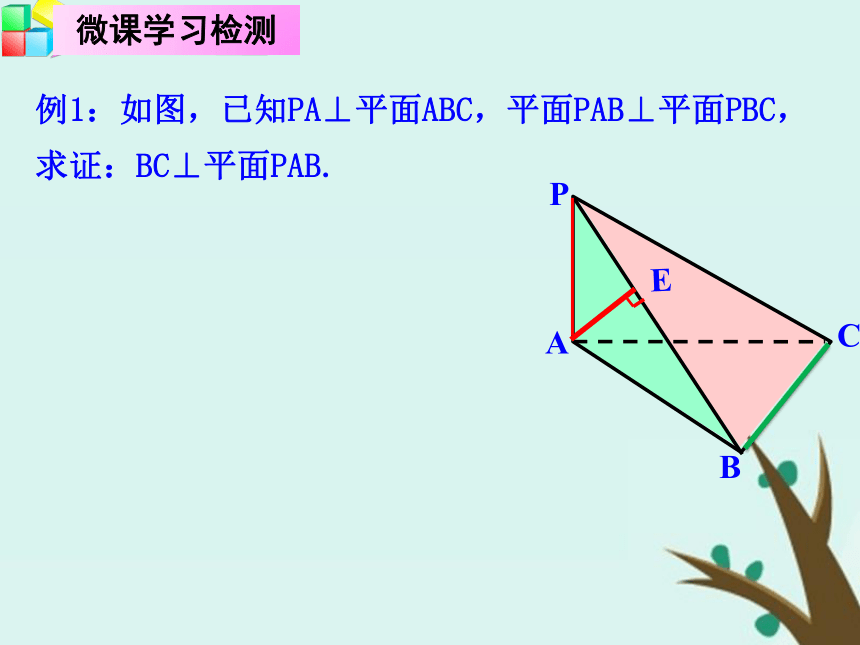
课件22张PPT。1.6.4 平面与平面垂直的性质例1:如图,已知PA⊥平面ABC,平面PAB⊥平面PBC,
求证:BC⊥平面PAB.EE例1:如图,已知PA⊥平面ABC,平面PAB⊥平面PBC,
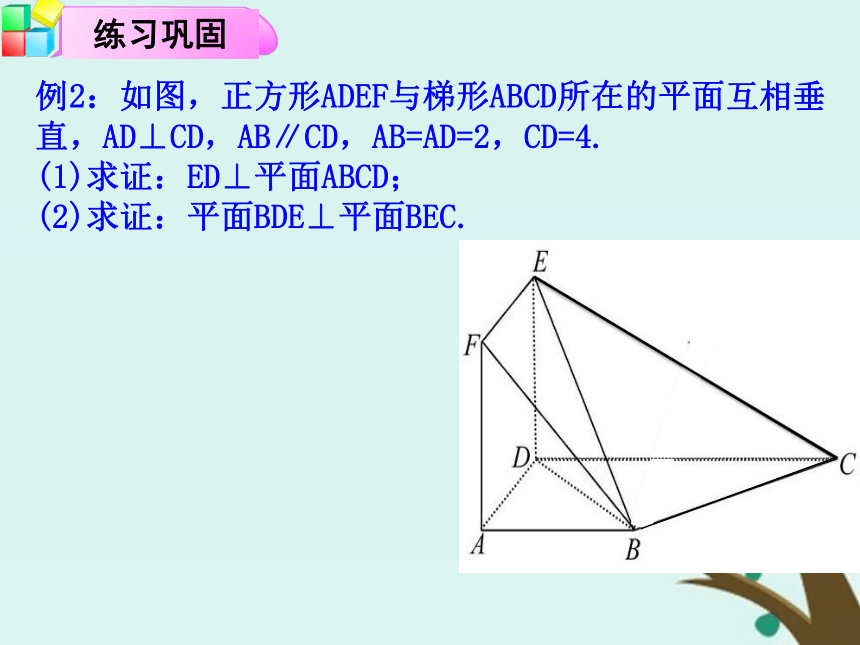
求证:BC⊥平面PAB.EE2.平面PAB⊥平面PBC,交线为PB,所以可在平面PAB内作 AE⊥PB.从而AE⊥平面PBC,所以AE⊥BC.见到面垂直面 分析:1.PA⊥平面ABC,所以PA⊥BC;想性质找交线找或作交线的垂线总结:例2:如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4.
(1)求证:ED⊥平面ABCD;
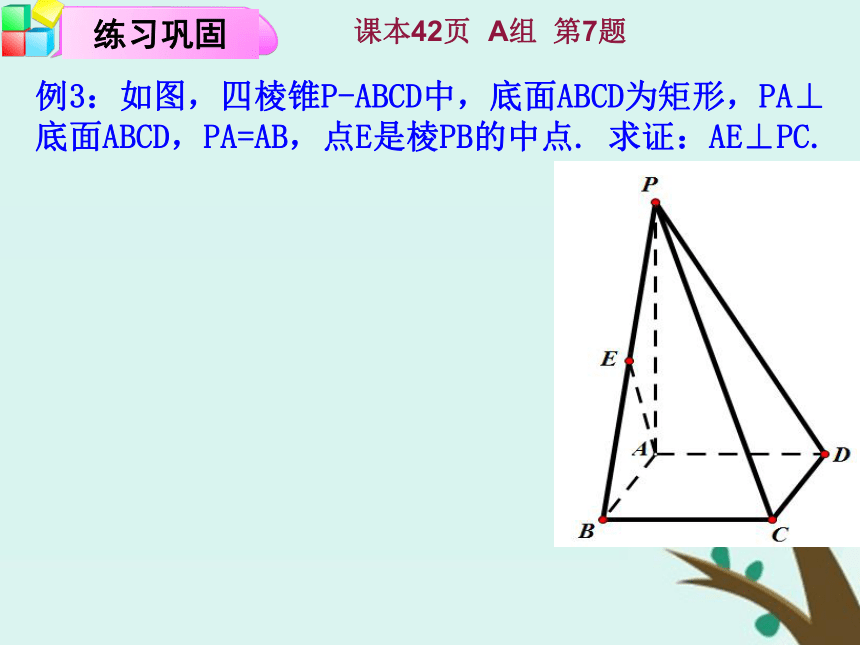
(2)求证:平面BDE⊥平面BEC.3233223例3:如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是棱PB的中点. 求证:AE⊥PC.课本42页 A组 第7题 线面垂直
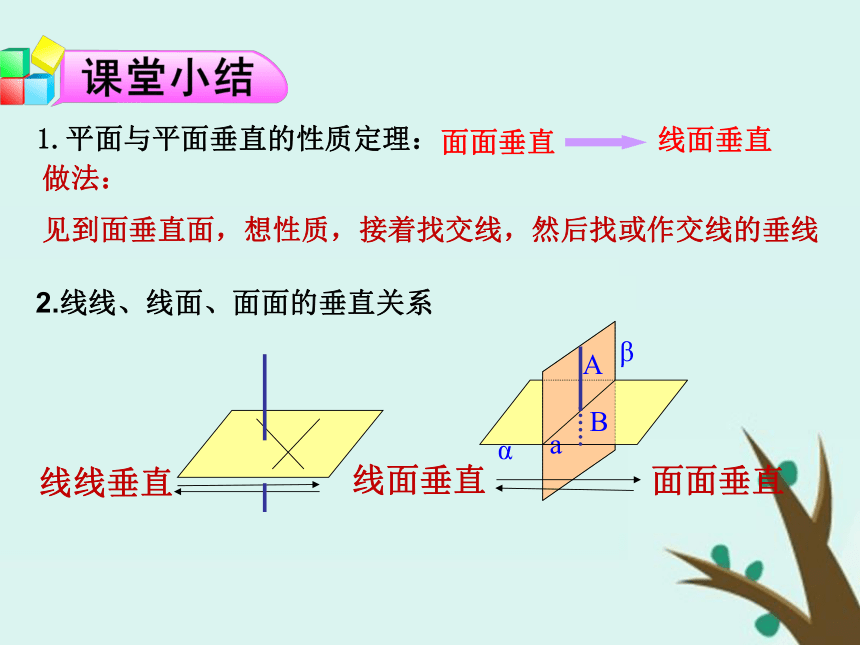
法一:面面垂直线面垂直线线垂直 法二:线面垂直线线垂直线面垂直线线垂直 线面垂直线线垂直例3:如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是棱PB的中点. 求证:AE⊥PC.课本42页 A组 第7题线线垂直线面垂直面面垂直2.线线、线面、面面的垂直关系1.平面与平面垂直的性质定理:做法:
见到面垂直面,想性质,接着找交线,然后找或作交线的垂线作业
1.测评38页 例1
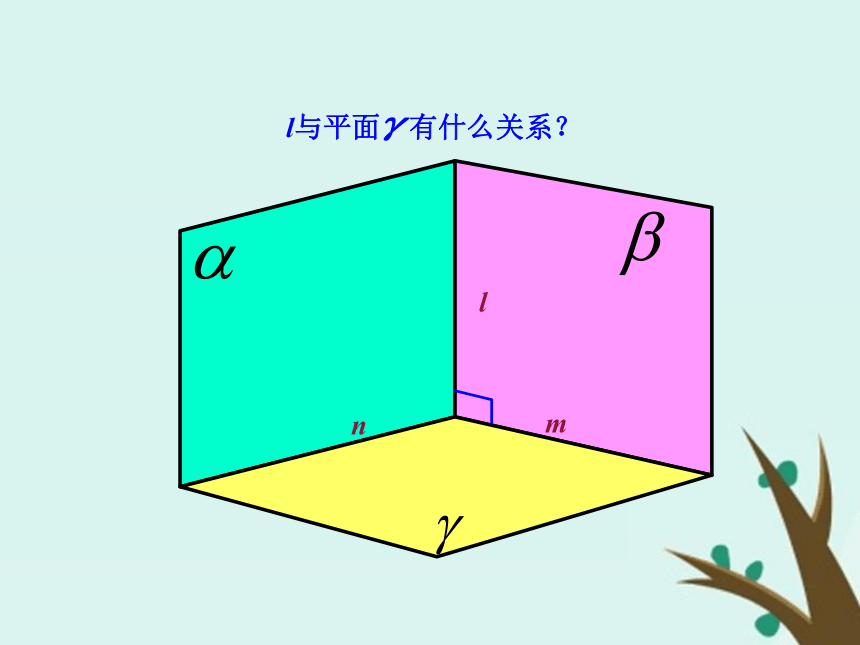
2.活页练156页 第9题lmn分析:作出图形.(法一)(法二)在γ内过A点作直线 a ⊥n,证法1:设在γ内过A点作直线 b⊥m,同理在γ内任取一点A(不在m,n上),在α内作直线a ⊥n证法2:设在β内作直线b⊥m如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.结论判断线面垂直的两种方法:
①线线垂直→线面垂直;
②面面垂直→线面垂直.如图:αβAbal分析:寻找平面α内与a平行的直线.解:在α内作垂直于 交线的直线b,
∵ ∴
∵ ∴a∥b.
又∵ ∴a∥α.
即直线a与平面α平行.结论:垂直于同一平面的直线和平面平行( ).αβAbalαβAbalB垂直思考 设平面 ⊥平面 ,点P在平面 内,过点P作平
面 的垂线a,直线a与平面 具有什么位置关系?aa直线a在平面 内两个平面垂直,则过某个平面内一点垂直于另一个平面的直线在该平面内.1.(2012·合肥模拟)设m、n是两条不同直线,α、β、γ是三个不同平面,给出下列四个命题,其中正确命题的序号是
①若m⊥α,n∥α,则m⊥n
②若α∥β,β∥γ,m⊥α,则m⊥γ
③若m∥α,m∥β,则α∥β
④若α⊥γ,β⊥γ,则α∥β
_①②
_____.解:①∵n∥α,∴过n的一个平面α′与α的交线n′平行于n,又∵m⊥α,∴m⊥n′,而n′∥n,∴m⊥n.
②∵α∥β,β∥γ,∴α∥γ,又∵m⊥α,∴m⊥γ.
③m∥α,m∥β,则α与β可能平行,也可能相交.
④α⊥γ,β⊥γ时,α与β可能平行,也可能相交.
答案:①②1.面面垂直的性质推论:a∥α2.已知两个平面垂直,下列命题中正确的有( ).①一个平面内已知直线必垂直于另一个平面内的任意直线;
②一个平面内的已知直线必垂直于另一个平面内的无数条
直线;
③一个平面内的任意一条直线必垂直于另一个平面;
④过一个平面内的任意一点做交线的垂线,则此垂线必垂直于另一个平面.
A.3个 B. 2个 C.1个 D.0个B3.下列命题中,正确的是( )A.过平面外一点,可作无数条直线和这个平面垂直
B.过一点有且仅有一个平面和一条定直线垂直
C.若a,b异面,过a一定可作一个平面与b垂直
D.a,b异面,过不在a,b上的点M,一定可以作一个平面
和a,b都垂直.?B
求证:BC⊥平面PAB.EE例1:如图,已知PA⊥平面ABC,平面PAB⊥平面PBC,
求证:BC⊥平面PAB.EE2.平面PAB⊥平面PBC,交线为PB,所以可在平面PAB内作 AE⊥PB.从而AE⊥平面PBC,所以AE⊥BC.见到面垂直面 分析:1.PA⊥平面ABC,所以PA⊥BC;想性质找交线找或作交线的垂线总结:例2:如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4.
(1)求证:ED⊥平面ABCD;
(2)求证:平面BDE⊥平面BEC.3233223例3:如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是棱PB的中点. 求证:AE⊥PC.课本42页 A组 第7题 线面垂直
法一:面面垂直线面垂直线线垂直 法二:线面垂直线线垂直线面垂直线线垂直 线面垂直线线垂直例3:如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB,点E是棱PB的中点. 求证:AE⊥PC.课本42页 A组 第7题线线垂直线面垂直面面垂直2.线线、线面、面面的垂直关系1.平面与平面垂直的性质定理:做法:
见到面垂直面,想性质,接着找交线,然后找或作交线的垂线作业
1.测评38页 例1
2.活页练156页 第9题lmn分析:作出图形.(法一)(法二)在γ内过A点作直线 a ⊥n,证法1:设在γ内过A点作直线 b⊥m,同理在γ内任取一点A(不在m,n上),在α内作直线a ⊥n证法2:设在β内作直线b⊥m如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面.结论判断线面垂直的两种方法:
①线线垂直→线面垂直;
②面面垂直→线面垂直.如图:αβAbal分析:寻找平面α内与a平行的直线.解:在α内作垂直于 交线的直线b,
∵ ∴
∵ ∴a∥b.
又∵ ∴a∥α.
即直线a与平面α平行.结论:垂直于同一平面的直线和平面平行( ).αβAbalαβAbalB垂直思考 设平面 ⊥平面 ,点P在平面 内,过点P作平
面 的垂线a,直线a与平面 具有什么位置关系?aa直线a在平面 内两个平面垂直,则过某个平面内一点垂直于另一个平面的直线在该平面内.1.(2012·合肥模拟)设m、n是两条不同直线,α、β、γ是三个不同平面,给出下列四个命题,其中正确命题的序号是
①若m⊥α,n∥α,则m⊥n
②若α∥β,β∥γ,m⊥α,则m⊥γ
③若m∥α,m∥β,则α∥β
④若α⊥γ,β⊥γ,则α∥β
_①②
_____.解:①∵n∥α,∴过n的一个平面α′与α的交线n′平行于n,又∵m⊥α,∴m⊥n′,而n′∥n,∴m⊥n.
②∵α∥β,β∥γ,∴α∥γ,又∵m⊥α,∴m⊥γ.
③m∥α,m∥β,则α与β可能平行,也可能相交.
④α⊥γ,β⊥γ时,α与β可能平行,也可能相交.
答案:①②1.面面垂直的性质推论:a∥α2.已知两个平面垂直,下列命题中正确的有( ).①一个平面内已知直线必垂直于另一个平面内的任意直线;
②一个平面内的已知直线必垂直于另一个平面内的无数条
直线;
③一个平面内的任意一条直线必垂直于另一个平面;
④过一个平面内的任意一点做交线的垂线,则此垂线必垂直于另一个平面.
A.3个 B. 2个 C.1个 D.0个B3.下列命题中,正确的是( )A.过平面外一点,可作无数条直线和这个平面垂直
B.过一点有且仅有一个平面和一条定直线垂直
C.若a,b异面,过a一定可作一个平面与b垂直
D.a,b异面,过不在a,b上的点M,一定可以作一个平面
和a,b都垂直.?B
