2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-1平行关系的判定课件(15张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-1平行关系的判定课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-16 20:47:50 | ||
图片预览




文档简介
课件15张PPT。直线与平面平行的判定
学习目标1、理解直线与平面平行的判定定理;
2、会用文字语言,图形语言、符号语言准确描述直线与平面平行的判定定理,并知道其地位和作用;
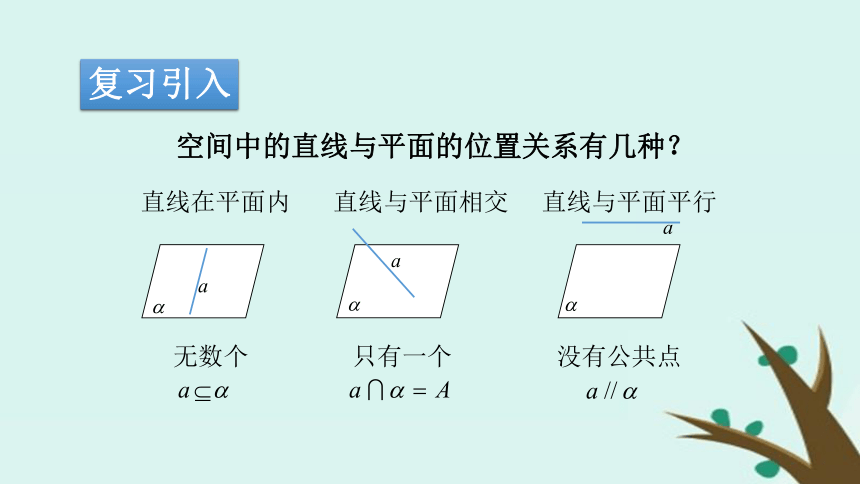
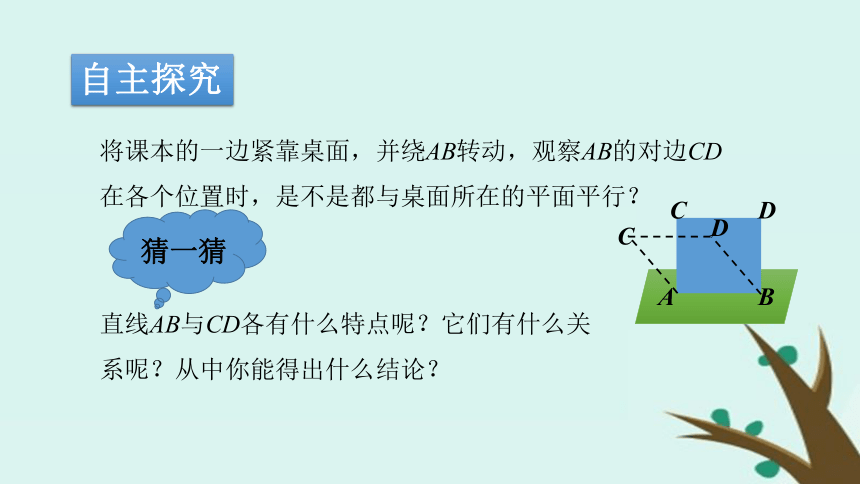
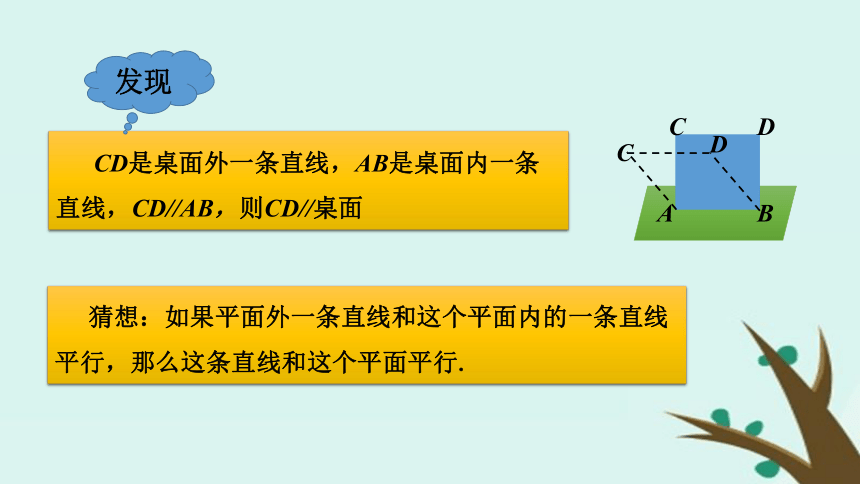
3、能运用判定定理证明一些空间直线与平面关系的简单问题.复习引入空间中的直线与平面的位置关系有几种?直线与平面相交直线与平面平行直线在平面内 无数个只有一个没有公共点实例感受在生活中有哪些直线与平面平行的例子,试举例说明. 在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇的一边与门框所在的平面给人以平行的印象.如何判定一条直线和一个平面平行呢? 可以利用定义“若直线与平面没有公共点,则直线与平面平行”进行判定.自主探究将课本的一边紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行? CD是桌面外一条直线,AB是桌面内一条直线,CD//AB,则CD//桌面 猜想:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.理性探究如图,如果平面 外直线 和平面 内的直线 平行,
(1)这两条直线共面吗?
(2)直线 与平面 会相交吗?共面不会相交抽象概括符号语言:注意:
1、定理三个条件缺一不可;
2、转化思想:线线平行→线面平行;
3、定理告诉我们:要证线面平行,只要在面内找一条直线,使线线平行.判定定理:若平面外一条直线与此平面内的一条直线平行,则
该直线与此平面平行.跟踪检测1判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例 (1)如果 是两条直线,且 ,那么 平行于经过 的任何平面; ( )
(2)如果直线 和平面 满足 ,那么 与 内的任何直线平行;
( )
(3)若两条直线都平行于同一个平面,那么这两条直线平行 ( )
(4)过平面外一点和这个平面平行的直线只有一条. ( )××××跟踪检测2例1、已知:空间四边形ABCD中,E,F分别是AB , AD的中点.
求证:EF//平面BCD例2、已知:空间四边形ABCD中,E,F分别是AB , AD的点.且 .
求证:EF//平面BCD例3、已知:如图所示,在正方体ABCD-A1B1C1D1中.
求证:BC1//平面AA1D1D方法归纳(1)直线与平面平行的判定定理的应用步骤:
①线与线平行 ②一条线在已知平面内
③一条线在已知平面外
(2)常见的证线线平行的三种途径:
①中位线→线线平行
②比例线段→线线平行
③平行四边形→线线平行(2017 全国卷Ⅱ)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD, E是PD的中点.证明:直线CE//平面PAB真题演练小结一、直线与平面平行的判定二、常见直线与直线平行的方法
①中位线定理
②比例线段
③平行四边形三、数学思想方法:转化的思想
学习目标1、理解直线与平面平行的判定定理;
2、会用文字语言,图形语言、符号语言准确描述直线与平面平行的判定定理,并知道其地位和作用;
3、能运用判定定理证明一些空间直线与平面关系的简单问题.复习引入空间中的直线与平面的位置关系有几种?直线与平面相交直线与平面平行直线在平面内 无数个只有一个没有公共点实例感受在生活中有哪些直线与平面平行的例子,试举例说明. 在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇的一边与门框所在的平面给人以平行的印象.如何判定一条直线和一个平面平行呢? 可以利用定义“若直线与平面没有公共点,则直线与平面平行”进行判定.自主探究将课本的一边紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行? CD是桌面外一条直线,AB是桌面内一条直线,CD//AB,则CD//桌面 猜想:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.理性探究如图,如果平面 外直线 和平面 内的直线 平行,
(1)这两条直线共面吗?
(2)直线 与平面 会相交吗?共面不会相交抽象概括符号语言:注意:
1、定理三个条件缺一不可;
2、转化思想:线线平行→线面平行;
3、定理告诉我们:要证线面平行,只要在面内找一条直线,使线线平行.判定定理:若平面外一条直线与此平面内的一条直线平行,则
该直线与此平面平行.跟踪检测1判断下列命题是否正确,若正确,请简述理由,若不正确,请给出反例 (1)如果 是两条直线,且 ,那么 平行于经过 的任何平面; ( )
(2)如果直线 和平面 满足 ,那么 与 内的任何直线平行;
( )
(3)若两条直线都平行于同一个平面,那么这两条直线平行 ( )
(4)过平面外一点和这个平面平行的直线只有一条. ( )××××跟踪检测2例1、已知:空间四边形ABCD中,E,F分别是AB , AD的中点.
求证:EF//平面BCD例2、已知:空间四边形ABCD中,E,F分别是AB , AD的点.且 .
求证:EF//平面BCD例3、已知:如图所示,在正方体ABCD-A1B1C1D1中.
求证:BC1//平面AA1D1D方法归纳(1)直线与平面平行的判定定理的应用步骤:
①线与线平行 ②一条线在已知平面内
③一条线在已知平面外
(2)常见的证线线平行的三种途径:
①中位线→线线平行
②比例线段→线线平行
③平行四边形→线线平行(2017 全国卷Ⅱ)如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD, E是PD的中点.证明:直线CE//平面PAB真题演练小结一、直线与平面平行的判定二、常见直线与直线平行的方法
①中位线定理
②比例线段
③平行四边形三、数学思想方法:转化的思想
