2018年高中数学北师大版必修2课件:第一章立体几何初步1-6-2垂直关系的性质课件(24张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-6-2垂直关系的性质课件(24张) |  | |
| 格式 | zip | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-16 20:46:07 | ||
图片预览





文档简介
课件24张PPT。平面与平面垂直的判定1.在立体几何中,"异面直线所成的角"是怎样定义的? 直线a、b是异面直线,经过空间任意一点O,分别引直线a' //a, b'// b,我们把相交直线a' 和 b'所成的锐角 (或直角)叫做异面直线所成的角。 2.在立体几何中,"直线和平面所成的角"是怎样定义的? 复习回顾平面的一条斜线和它在平面上的射影所成的锐角,
叫做这条直线和这个平面所成的角。问题:异面直线所成的角、直线和平面所成的角有什么共同的特征?结论:它们的共同特征都是将三维空间的角转化为二维空间的角,即平面角。 两异面直线所成角的取值范围:( 0o, 90o ].
直线和平面所成角的取值范围:[ 0o, 90o ].1.半平面的定义讲授新课1.半平面的定义 平面内的一条直线把平面分为两部
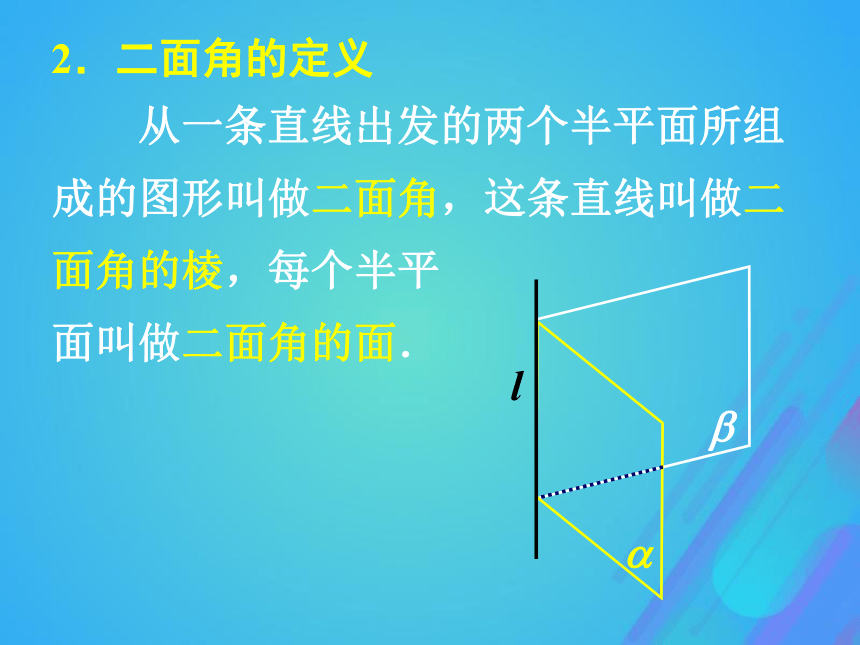
分,其中的每一部分都叫做半平面.讲授新课2.二面角的定义 从一条直线出发的两个半平面所组
成的图形叫做二面角,这条直线叫做二
面角的棱,每个半平
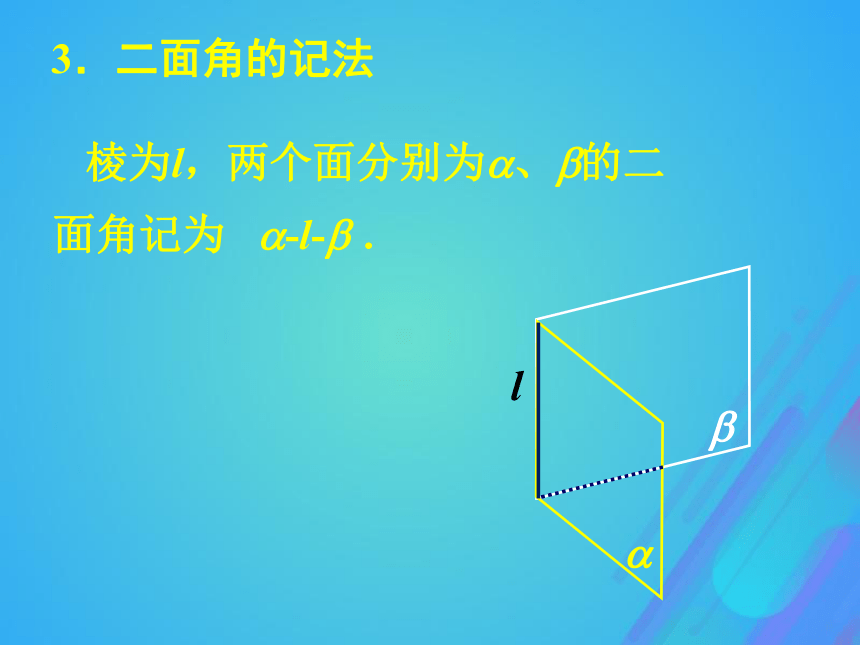
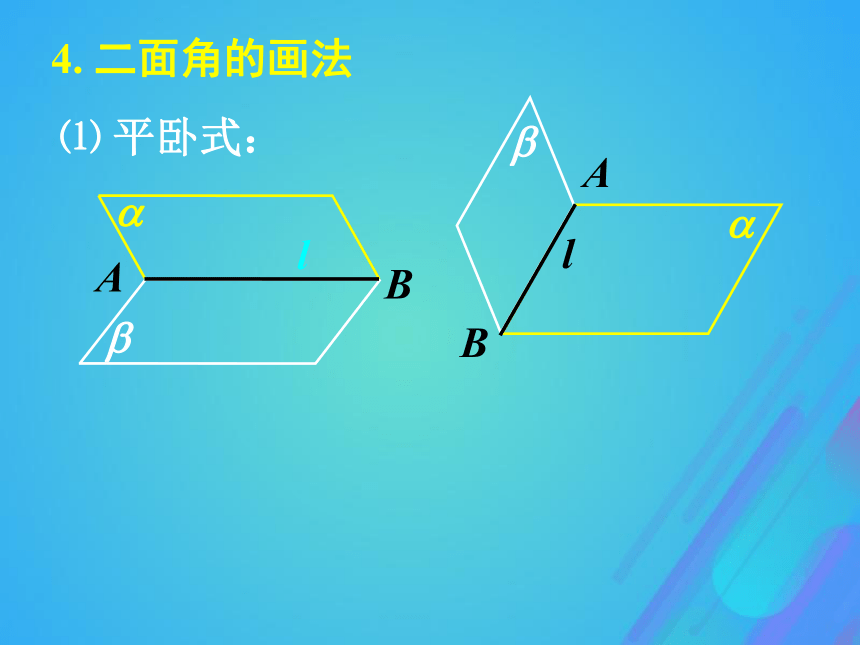
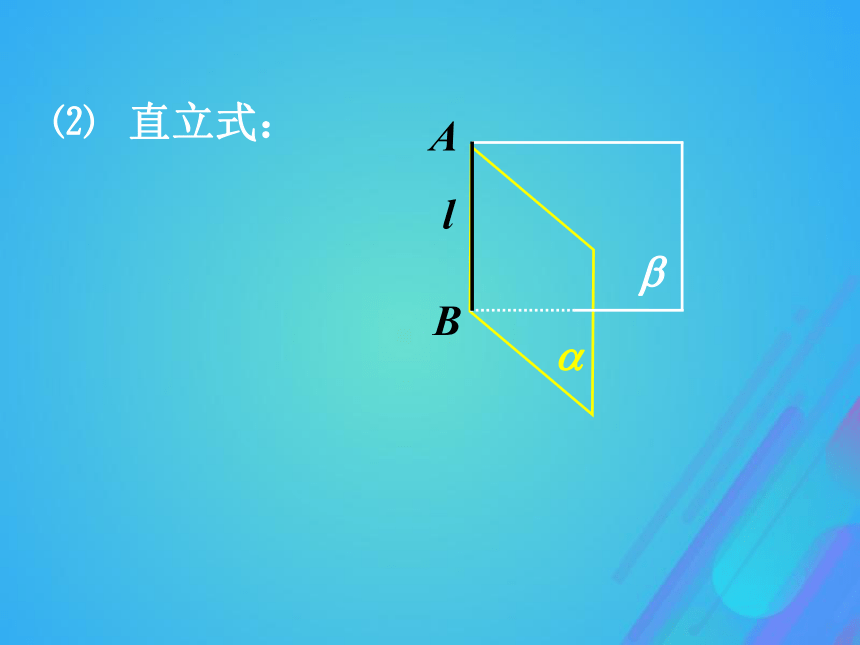
面叫做二面角的面.l?? 棱为l,两个面分别为?、?的二面角记为 ?-l-? .3.二面角的记法⑴ 平卧式:l4. 二面角的画法⑵ 直立式: 在二面角?-l-?的
棱l上任取一点O,如
图,在半平面 ? 和 ?
内,从点 O 分别作垂
直于棱 l 的射线OA、
OB,射线OA、OB组成∠AOB. 怎样度量二面角的大小?能否转化为两相交直线所成的角?4.二面角的大小 一个平面垂直于二
面角 ?-l-? 的棱 l,且与
两个半平面的交线分别
是射线 OA、OB,O 为
垂足,则 ∠AOB 叫做
二面角 ?-l-? 的平面角.4.二面角的大小备注:∠AOB的大小一定. 二面角的大小可以用它的平面角来
度量.即二面角的平面角是多少度,就
说这个二面角是多少度.二面角的范围:[ 0o, 180o ].① 二面角的两个面重合: 0o;② 二面角的两个面合成一个平面:180o;4.二面角的大小③ 平面角是直角的二面角叫直二面角.(1)定义法
根据定义作出来(2)垂面法
作与棱垂直的平面与
两半平面的交线得到??l?ABO??lOABAO??lD(3)三垂线法5. 二面角的平面角的作法例1.在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角 D’-AB-D;
(2)二面角 C’-BD-C.例题讲解(1)二面角 D’-AB-D的平面角: ∠C’BC(2)二面角 C’-BD-C的平面角: ∠C’OC
6. 平面与平面垂直 两个平面相交,如果它们所成的二
面角是直二面角,就说这两个平面互相
垂直. 平面?与?垂直,记作?⊥?. 6. 平面与平面垂直 两个平面相交,如果它们所成的二
面角是直二面角,就说这两个平面互相
垂直. 平面?与?垂直,记作?⊥?. ????两个平面垂直的判定定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直. 例1 如图,AB是⊙O的直径, PA垂直于
⊙O所在的平面,C是圆周上不同于A, B
的任意一点,求证:平面PAC⊥平面PBC. 例1 如图,AB是⊙O的直径, PA垂直于
⊙O所在的平面,C是圆周上不同于A, B
的任意一点,求证:平面PAC⊥平面PBC. 线线垂直
→线面垂直→面面垂直 例2:如图,已知三棱锥D-ABC的三
个侧面与底面全等,且AB=AC= ,
BC=2,求以BC为棱,以面BCD与面
BCA为面的二面角的大小?DAECB练习: ABCD是正方形,O是正方形的
中心,PO⊥平面ABCD , E是PC的中点,
求证:平面PAC⊥平面BDE.POABCDE课堂小结1. 二面角的定义、二面角的平面角;
2. 二面角平面角的求法;
3. 平面与平面垂直的判定.
叫做这条直线和这个平面所成的角。问题:异面直线所成的角、直线和平面所成的角有什么共同的特征?结论:它们的共同特征都是将三维空间的角转化为二维空间的角,即平面角。 两异面直线所成角的取值范围:( 0o, 90o ].
直线和平面所成角的取值范围:[ 0o, 90o ].1.半平面的定义讲授新课1.半平面的定义 平面内的一条直线把平面分为两部
分,其中的每一部分都叫做半平面.讲授新课2.二面角的定义 从一条直线出发的两个半平面所组
成的图形叫做二面角,这条直线叫做二
面角的棱,每个半平
面叫做二面角的面.l?? 棱为l,两个面分别为?、?的二面角记为 ?-l-? .3.二面角的记法⑴ 平卧式:l4. 二面角的画法⑵ 直立式: 在二面角?-l-?的
棱l上任取一点O,如
图,在半平面 ? 和 ?
内,从点 O 分别作垂
直于棱 l 的射线OA、
OB,射线OA、OB组成∠AOB. 怎样度量二面角的大小?能否转化为两相交直线所成的角?4.二面角的大小 一个平面垂直于二
面角 ?-l-? 的棱 l,且与
两个半平面的交线分别
是射线 OA、OB,O 为
垂足,则 ∠AOB 叫做
二面角 ?-l-? 的平面角.4.二面角的大小备注:∠AOB的大小一定. 二面角的大小可以用它的平面角来
度量.即二面角的平面角是多少度,就
说这个二面角是多少度.二面角的范围:[ 0o, 180o ].① 二面角的两个面重合: 0o;② 二面角的两个面合成一个平面:180o;4.二面角的大小③ 平面角是直角的二面角叫直二面角.(1)定义法
根据定义作出来(2)垂面法
作与棱垂直的平面与
两半平面的交线得到??l?ABO??lOABAO??lD(3)三垂线法5. 二面角的平面角的作法例1.在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角 D’-AB-D;
(2)二面角 C’-BD-C.例题讲解(1)二面角 D’-AB-D的平面角: ∠C’BC(2)二面角 C’-BD-C的平面角: ∠C’OC
6. 平面与平面垂直 两个平面相交,如果它们所成的二
面角是直二面角,就说这两个平面互相
垂直. 平面?与?垂直,记作?⊥?. 6. 平面与平面垂直 两个平面相交,如果它们所成的二
面角是直二面角,就说这两个平面互相
垂直. 平面?与?垂直,记作?⊥?. ????两个平面垂直的判定定理 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直. 例1 如图,AB是⊙O的直径, PA垂直于
⊙O所在的平面,C是圆周上不同于A, B
的任意一点,求证:平面PAC⊥平面PBC. 例1 如图,AB是⊙O的直径, PA垂直于
⊙O所在的平面,C是圆周上不同于A, B
的任意一点,求证:平面PAC⊥平面PBC. 线线垂直
→线面垂直→面面垂直 例2:如图,已知三棱锥D-ABC的三
个侧面与底面全等,且AB=AC= ,
BC=2,求以BC为棱,以面BCD与面
BCA为面的二面角的大小?DAECB练习: ABCD是正方形,O是正方形的
中心,PO⊥平面ABCD , E是PC的中点,
求证:平面PAC⊥平面BDE.POABCDE课堂小结1. 二面角的定义、二面角的平面角;
2. 二面角平面角的求法;
3. 平面与平面垂直的判定.
