整理与复习 数与代数(二)·简易方程课件 (共31张PPT)
文档属性
| 名称 | 整理与复习 数与代数(二)·简易方程课件 (共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 322.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-17 14:59:44 | ||
图片预览










文档简介
课件31张PPT。数与代数(二)RJ 五年级上册 简易方程a×9= 3a+5a=
7y+4y-10y= 2.58÷2=
0.7×0.32= 6.3÷7=
1.6×3= 0.072÷0.6=9a8ay1.290.2240.94.80.12知识梳理深化知识拓展延伸(1)字母表达式:意义、写法、代值入式、计算。
(2)方程的:意义、性质、解方程。
(3)用方程解决问题。简易方程运算定律计算公式数量关系方程的意义解方程稍复杂的方程用字母表示数解简易方程列方程解决问题基本的方程方程方程的解解方程加法交换律:
加法结合律:
乘法交换律:
乘法结合律:
乘法分配律:a+b = b+a
(a+b ) +c = a+(b+c)
a×b = b×a
(a×b ) ×c = a×(b×c)
(a+b ) ×c = a×c+b×c)用字母表示定律方程和等式(1)等式的意义:表示等号两边是相等关系的式子叫等式。(2)方程的意义:含有未知数的等式叫方程。(3)方程与等式的关系:等式的范围比方程的范围大。
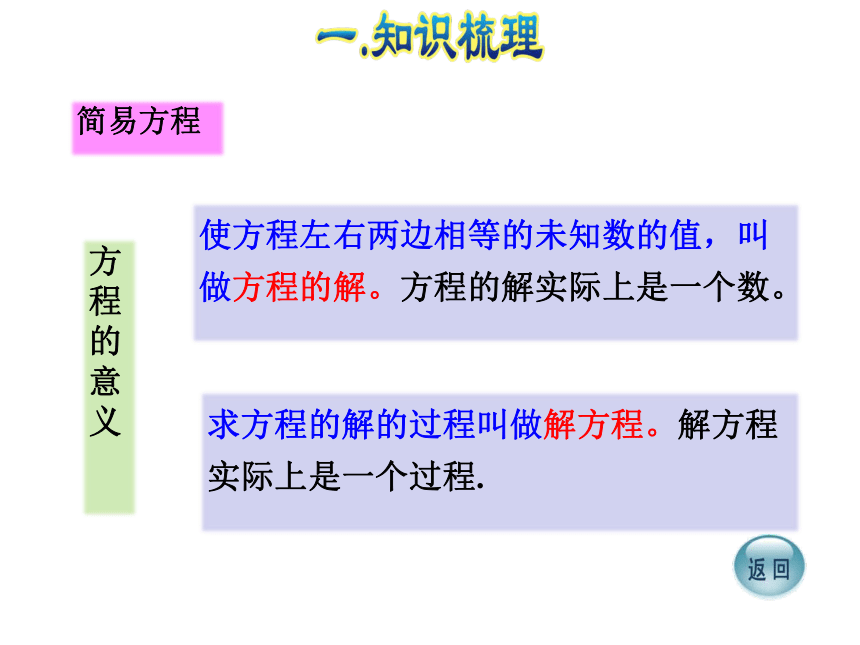
方程都是等式,但等式不一定是方程。简易方程方程的意义使方程左右两边相等的未知数的值,叫做方程的解。方程的解实际上是一个数。 求方程的解的过程叫做解方程。解方程实际上是一个过程.简易方程1.省略乘号写出下面各式a×x= x×x= b×8= 3×d= b×1= 注意:
①当字母与数字相乘时,去掉乘号,把数字写在字母的前面,也可以用点表示乘号。
②当字母与字母相乘时,省略乘号,用点表示或直接去掉乘号。axx28b3db1、用字母表示数及数量关系1.省略乘号写出下面各式a×x= x×x= b×8= 3×d= b×1= 注意:
③字母与1相乘省略1不写,只写字母本身。
④两个一样的字母相乘就写一个字母,再在字母的右上角写上2。axx28b3db1、用字母表示数及数量关系2.一个平行四边形的底是a厘米,高3厘米,它的面积是( )平方厘米。S =ah
=3a 3a1、用字母表示数及数量关系2.一个长方形的长是48分米,宽是b分米,它的周长是( )分米。C =(a+b )×2
=(48+b)×2
=96+2b96+2b3.小英重n千克,比小华轻3千克,小华体重是( )千克。小华比小英重3千克3+n4.汽车平均每小时行m千米,6小时能行( )千米,行450千米要( )小时。S=vt
=6m6m t=S÷v
=450÷m450÷m5.学校美术组有x人,体育组的人数是美术组人数的4倍,体育组有( )人。当x=15时,体育组有( )人。4x=4×15=60 4x 606.一头奶牛一天可以产奶y千克,6头奶牛一周可以产奶( )千克。工作总量=工作效率 ×工作时间(C=at ) 一头奶牛一周的产奶总量=y×76头奶牛一周的产奶总量=y×7×6=42y 42y2x+13=272x+13-13=27-132x=142x÷2=14÷2x=7解:解:(2x+x)×2=4.83x×2=4.83x×2=4.86x=4.8x=0.86x÷6=4.8÷63、解方程解方程注意事项:
①等式的两边同时加上或减去相同的数,等式不变。(同加同减)。
②等式的两边同时乘或除以相同的数(0除外),等式不变。(同乘同除)
③在解方程是一定要写上解字。思考:列方程解决问题的步骤是什么?1.小明的妈妈今年的年龄是小明的3倍,妈妈比小明大24岁,小明和他的妈妈今年分别是多少岁?4、列方程解应用题答:妈妈36岁,小明12岁。妈妈:12×3=36(岁) 3x-x=242x=24x=12妈妈的年龄-小明的年龄=242x÷2=24÷2解:设小明的年龄x岁。1.小明的妈妈今年的年龄是小明的3倍,妈妈比小明大24岁,小明和他的妈妈今年分别是多少岁?2.食堂买来茄子和土豆共380 kg,茄子的质量比土豆的3倍还多8 kg,茄子和土豆各有多少千克?解:设土豆有x千克
x+3x+8=380
4x=372
x=93 93×3+8=287(千克)
答:茄子有287千克,土豆有93千克.3.一条隧道长960 m,甲、乙两施工队,从两边同时开挖,甲队每天可挖3 m,乙队每天可挖5 m,多少天能完成这条隧道?解:设x天能够完成工程,
3x+5x=960
(3+5)x=960
8x=960
8x÷8=960÷8
x=120
答:120天能够完成工程。3.一条隧道长960 m,甲、乙两施工队,从两边同时开挖,甲队每天可挖3 m,乙队每天可挖5 m,多少天能完成这条隧道?解析:列出方程,解ax+bx=c类型方程.
解析
根据总工程量=甲队每天工作量×天数+乙队每天工作量×天数,列出方程.4.甲、乙两车从相距486千米的两地同时出发,相向而行,经过3.6小时相遇。已知甲车每小时比乙车慢15千米。乙车每小时行多少千米?3.6x+3.6×(x-15)=486
3.6x+3.6x-54=486
7.2x=540
x=75
答:乙车每小时行75千米.解:假设乙车每小时行x千米,则甲车每小时行(x-15)千米,可得:列方程解决问题的步骤(1)设未知数(2)根据等量关系列方程(3)解方程(4)检验、写答1.填空.(1)明明有3个银币,每个硬币n元,明明有( )元.
(2)车上原来有x人,中途有8人下车,现在车上有( )人。3n8b(3)有8袋金鱼,每袋有b条,一共有( )条。
(4)有m个饺子,每盘12个,可以装( )盘。
(5)小明每天跑步m公里,小强每天跑步n公里,两个人每天共跑( )公里。15天共跑( )公里。x-8m÷12m+n15(m+n)2.连一连。比 a 多 2的数比a 少 2 的数2个a相加的和2个a相乘的积 a 的 2 倍 a2 2a a+2 a-2 3.解方程。(任选两题检验)
2x-7.5=8.5 8(x-6.2)=41.6 解: x=8解: x=11.4解: x=1.4解: x=407(5x+6)=91 12÷x=0.34.判断。
(1)a×b×8可以简写成ab8。 ( )
(2)x+5=4×5是方程。 ( )
(3)方程一定是等式。 ( )
(4)a的平方等于2个a相加。 ( )
(5)a÷b中,a、b可以是任何数。 ( )5.米仓今天要运走55吨大米,每次能运五吨,上午运了四次,下午要运几次才能运完。解:设下午要运x次才能运完。(4+x)×5=55x=7答:下午要运7次才能运完。6.学校买10套课桌用1200元,已知桌子的单价是凳子的4倍,每张桌子多少元?(桌子的单价+凳子的单价)×10=总价答:每张桌子单价是96元。5x×10=120024×4=96(元)(4x+x)×10=120050x=120050x÷50=1200÷50x=24解:设凳子的单价为x元。
7y+4y-10y= 2.58÷2=
0.7×0.32= 6.3÷7=
1.6×3= 0.072÷0.6=9a8ay1.290.2240.94.80.12知识梳理深化知识拓展延伸(1)字母表达式:意义、写法、代值入式、计算。
(2)方程的:意义、性质、解方程。
(3)用方程解决问题。简易方程运算定律计算公式数量关系方程的意义解方程稍复杂的方程用字母表示数解简易方程列方程解决问题基本的方程方程方程的解解方程加法交换律:
加法结合律:
乘法交换律:
乘法结合律:
乘法分配律:a+b = b+a
(a+b ) +c = a+(b+c)
a×b = b×a
(a×b ) ×c = a×(b×c)
(a+b ) ×c = a×c+b×c)用字母表示定律方程和等式(1)等式的意义:表示等号两边是相等关系的式子叫等式。(2)方程的意义:含有未知数的等式叫方程。(3)方程与等式的关系:等式的范围比方程的范围大。
方程都是等式,但等式不一定是方程。简易方程方程的意义使方程左右两边相等的未知数的值,叫做方程的解。方程的解实际上是一个数。 求方程的解的过程叫做解方程。解方程实际上是一个过程.简易方程1.省略乘号写出下面各式a×x= x×x= b×8= 3×d= b×1= 注意:
①当字母与数字相乘时,去掉乘号,把数字写在字母的前面,也可以用点表示乘号。
②当字母与字母相乘时,省略乘号,用点表示或直接去掉乘号。axx28b3db1、用字母表示数及数量关系1.省略乘号写出下面各式a×x= x×x= b×8= 3×d= b×1= 注意:
③字母与1相乘省略1不写,只写字母本身。
④两个一样的字母相乘就写一个字母,再在字母的右上角写上2。axx28b3db1、用字母表示数及数量关系2.一个平行四边形的底是a厘米,高3厘米,它的面积是( )平方厘米。S =ah
=3a 3a1、用字母表示数及数量关系2.一个长方形的长是48分米,宽是b分米,它的周长是( )分米。C =(a+b )×2
=(48+b)×2
=96+2b96+2b3.小英重n千克,比小华轻3千克,小华体重是( )千克。小华比小英重3千克3+n4.汽车平均每小时行m千米,6小时能行( )千米,行450千米要( )小时。S=vt
=6m6m t=S÷v
=450÷m450÷m5.学校美术组有x人,体育组的人数是美术组人数的4倍,体育组有( )人。当x=15时,体育组有( )人。4x=4×15=60 4x 606.一头奶牛一天可以产奶y千克,6头奶牛一周可以产奶( )千克。工作总量=工作效率 ×工作时间(C=at ) 一头奶牛一周的产奶总量=y×76头奶牛一周的产奶总量=y×7×6=42y 42y2x+13=272x+13-13=27-132x=142x÷2=14÷2x=7解:解:(2x+x)×2=4.83x×2=4.83x×2=4.86x=4.8x=0.86x÷6=4.8÷63、解方程解方程注意事项:
①等式的两边同时加上或减去相同的数,等式不变。(同加同减)。
②等式的两边同时乘或除以相同的数(0除外),等式不变。(同乘同除)
③在解方程是一定要写上解字。思考:列方程解决问题的步骤是什么?1.小明的妈妈今年的年龄是小明的3倍,妈妈比小明大24岁,小明和他的妈妈今年分别是多少岁?4、列方程解应用题答:妈妈36岁,小明12岁。妈妈:12×3=36(岁) 3x-x=242x=24x=12妈妈的年龄-小明的年龄=242x÷2=24÷2解:设小明的年龄x岁。1.小明的妈妈今年的年龄是小明的3倍,妈妈比小明大24岁,小明和他的妈妈今年分别是多少岁?2.食堂买来茄子和土豆共380 kg,茄子的质量比土豆的3倍还多8 kg,茄子和土豆各有多少千克?解:设土豆有x千克
x+3x+8=380
4x=372
x=93 93×3+8=287(千克)
答:茄子有287千克,土豆有93千克.3.一条隧道长960 m,甲、乙两施工队,从两边同时开挖,甲队每天可挖3 m,乙队每天可挖5 m,多少天能完成这条隧道?解:设x天能够完成工程,
3x+5x=960
(3+5)x=960
8x=960
8x÷8=960÷8
x=120
答:120天能够完成工程。3.一条隧道长960 m,甲、乙两施工队,从两边同时开挖,甲队每天可挖3 m,乙队每天可挖5 m,多少天能完成这条隧道?解析:列出方程,解ax+bx=c类型方程.
解析
根据总工程量=甲队每天工作量×天数+乙队每天工作量×天数,列出方程.4.甲、乙两车从相距486千米的两地同时出发,相向而行,经过3.6小时相遇。已知甲车每小时比乙车慢15千米。乙车每小时行多少千米?3.6x+3.6×(x-15)=486
3.6x+3.6x-54=486
7.2x=540
x=75
答:乙车每小时行75千米.解:假设乙车每小时行x千米,则甲车每小时行(x-15)千米,可得:列方程解决问题的步骤(1)设未知数(2)根据等量关系列方程(3)解方程(4)检验、写答1.填空.(1)明明有3个银币,每个硬币n元,明明有( )元.
(2)车上原来有x人,中途有8人下车,现在车上有( )人。3n8b(3)有8袋金鱼,每袋有b条,一共有( )条。
(4)有m个饺子,每盘12个,可以装( )盘。
(5)小明每天跑步m公里,小强每天跑步n公里,两个人每天共跑( )公里。15天共跑( )公里。x-8m÷12m+n15(m+n)2.连一连。比 a 多 2的数比a 少 2 的数2个a相加的和2个a相乘的积 a 的 2 倍 a2 2a a+2 a-2 3.解方程。(任选两题检验)
2x-7.5=8.5 8(x-6.2)=41.6 解: x=8解: x=11.4解: x=1.4解: x=407(5x+6)=91 12÷x=0.34.判断。
(1)a×b×8可以简写成ab8。 ( )
(2)x+5=4×5是方程。 ( )
(3)方程一定是等式。 ( )
(4)a的平方等于2个a相加。 ( )
(5)a÷b中,a、b可以是任何数。 ( )5.米仓今天要运走55吨大米,每次能运五吨,上午运了四次,下午要运几次才能运完。解:设下午要运x次才能运完。(4+x)×5=55x=7答:下午要运7次才能运完。6.学校买10套课桌用1200元,已知桌子的单价是凳子的4倍,每张桌子多少元?(桌子的单价+凳子的单价)×10=总价答:每张桌子单价是96元。5x×10=120024×4=96(元)(4x+x)×10=120050x=120050x÷50=1200÷50x=24解:设凳子的单价为x元。
