必修2 1.3 空间几何体表面积与体积第一课时课件(38张PPT)
文档属性
| 名称 | 必修2 1.3 空间几何体表面积与体积第一课时课件(38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-16 22:09:22 | ||
图片预览





文档简介
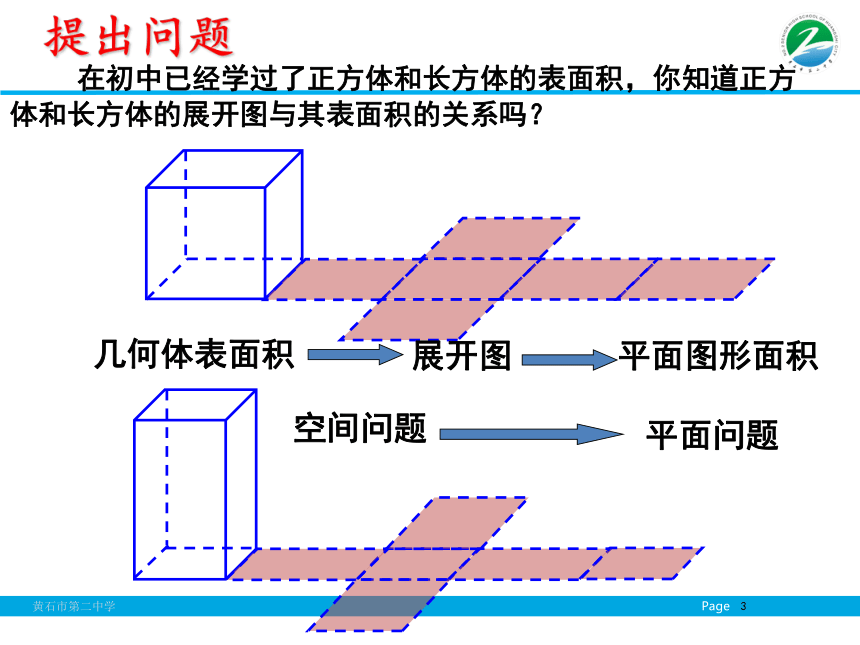
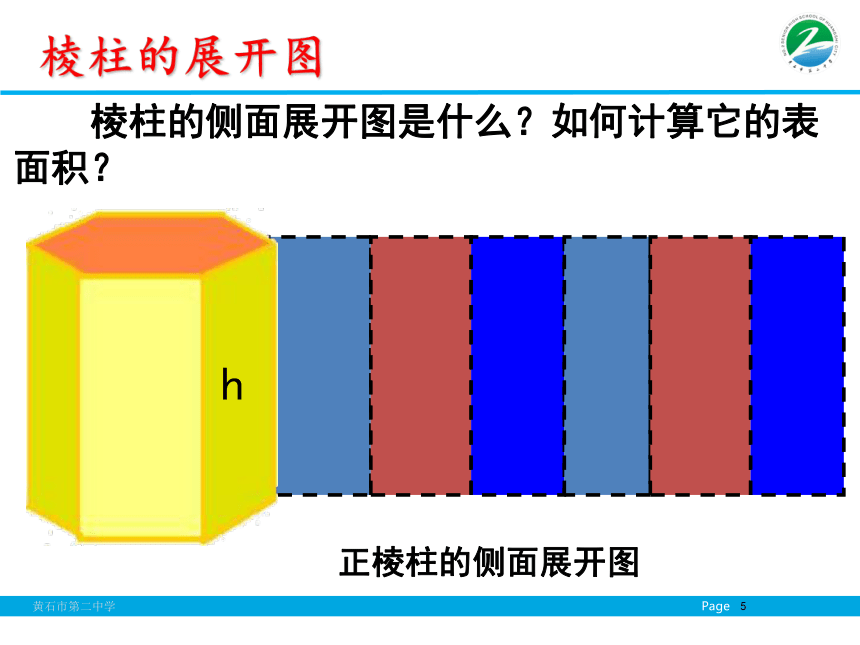
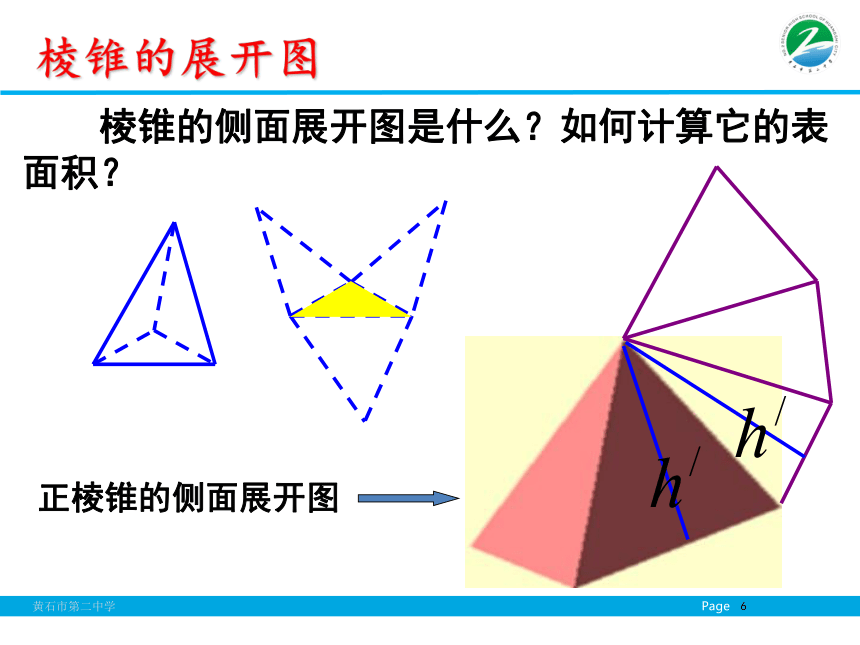
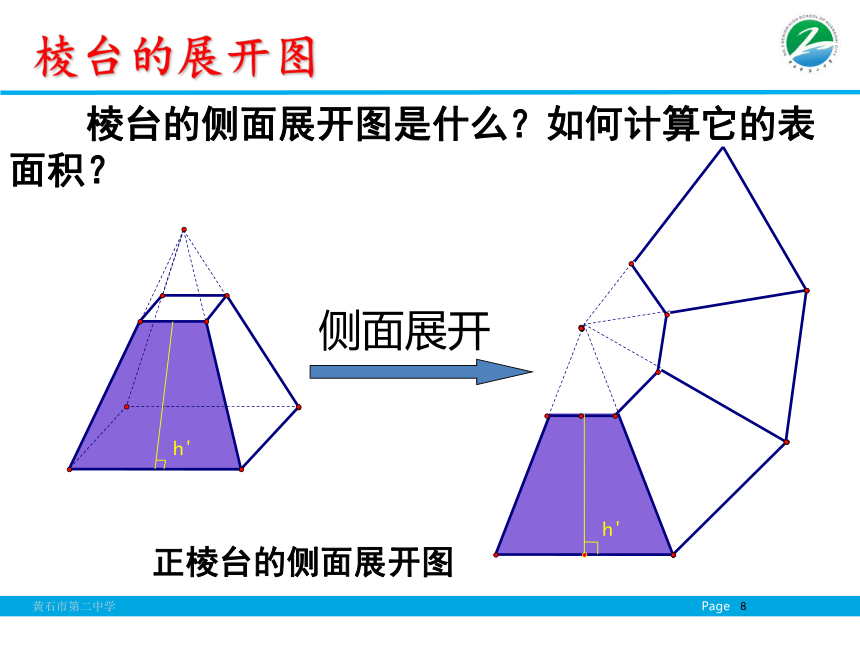
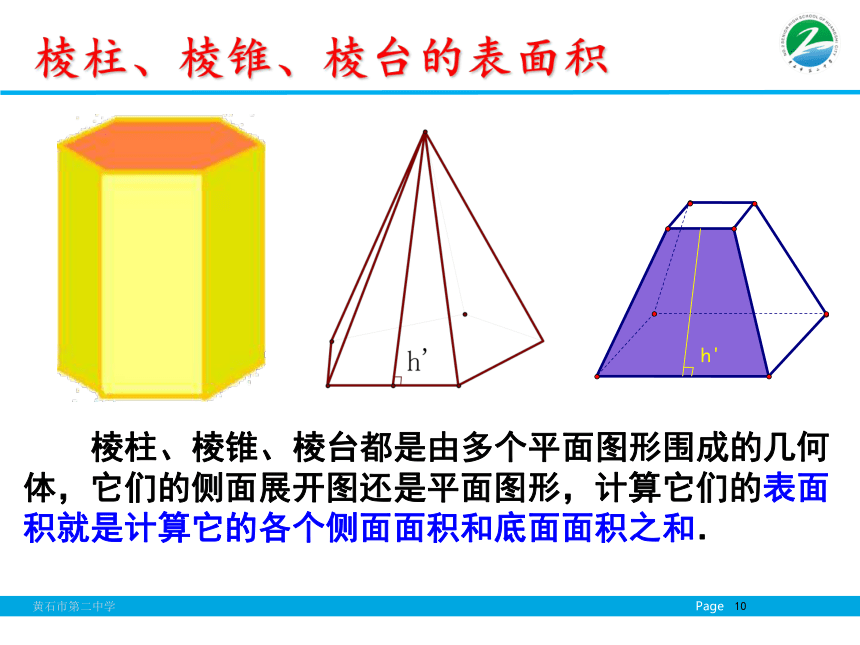
课件38张PPT。1.3.1柱体、锥体、台体的表面积和体积必修二第一章空间几何体第三节第一课时北京奥运会场馆图 在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?几何体表面积提出问题 正方体、长方体是由多个平面围成的几何体,它们的表面积就是各个面的面积的和. 因此,我们可以把多面体展成平面图形,利用平面图形求面积的方法,求多面体的表面积.引入新课 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积呢? 圆柱、圆锥、圆台它们的展开图是什么?如何计算它们的表面积呢?探究 棱柱的侧面展开图是什么?如何计算它的表面积?棱柱的展开图正棱柱的侧面展开图 棱锥的侧面展开图是什么?如何计算它的表面积?棱锥的展开图 例1:已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积 . 分析:四面体的展开图是由四个全等的正三角形组成.因此,四面体S-ABC 的表面积 .,交BC于点D.典型例题 棱台的侧面展开图是什么?如何计算它的表面积?棱台的展开图侧面展开正棱台的侧面展开图 棱柱的侧面展开图是由平行四边形组成的平面图形,
棱锥的侧面展开图是由三角形组成的平面图形,
棱台的侧面展开图是由梯形组成的平面图形.
这样,求它们的表面积的问题就可转化为求平行四边形、
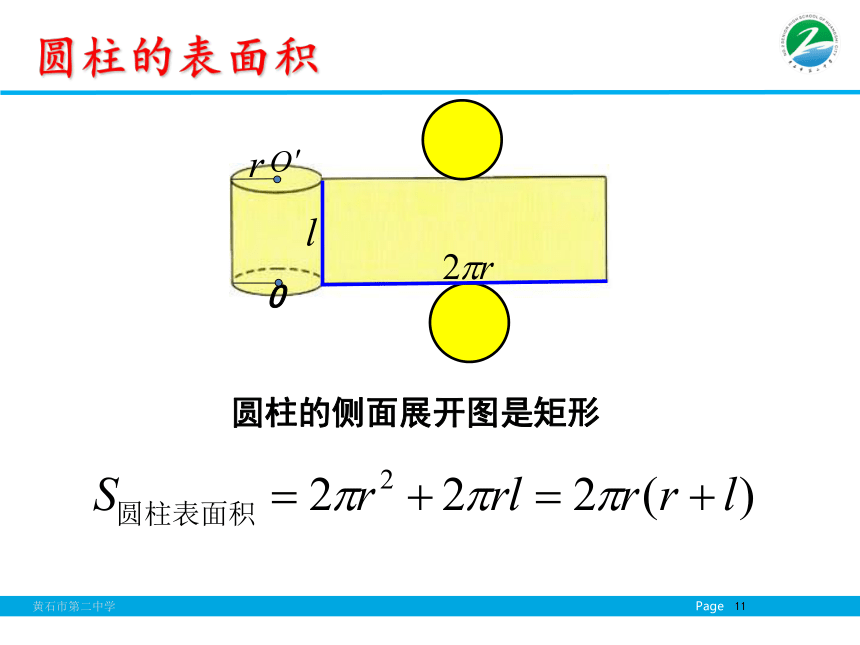
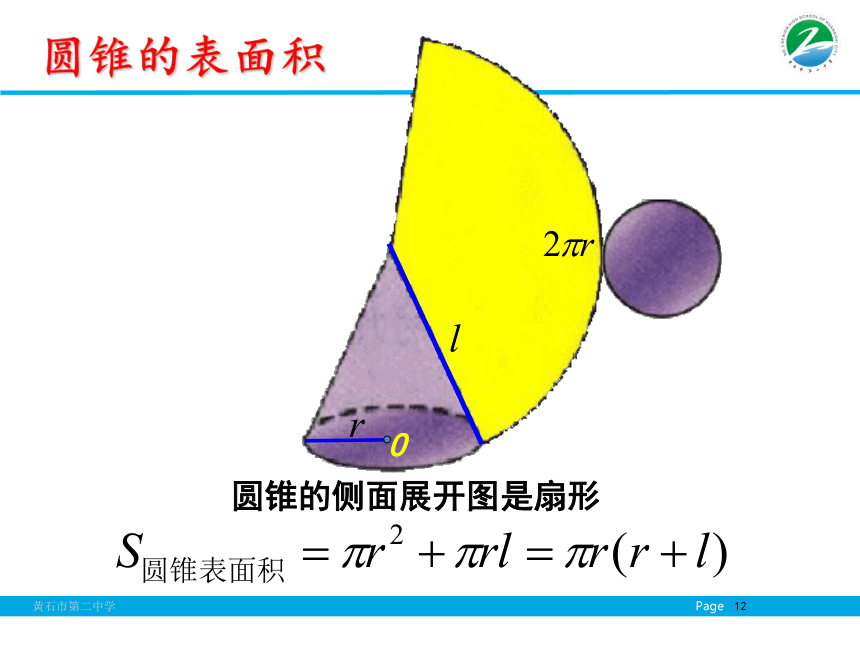
三角形、梯形的面积问题.棱柱、棱锥、棱台的表面积 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.圆柱的表面积圆柱的侧面展开图是矩形圆锥的表面积圆锥的侧面展开图是扇形圆台的表面积 参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 ?圆台的侧面展开图是扇环三者之间关系 圆柱、圆锥、圆台三者的表面积公式之间有什么关系?12/17/2018例2.一个圆台形花盆盆口直径为20cm,盆底直径为15cm,底部渗水孔直径为1.5cm,盆壁长15cm.为美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆,需要多少油漆.(精确到1毫升,可用计算器) 典型例题花盆外壁的面积=花盆的侧面积+底面积-底面圆孔面积等底等高的三角形面积相等等面积法:温故新知等底面积、等高的两个柱体是否体积相等?类比 取一些书堆放在桌面上(如图所示) ,并改变它们的放置方法,观察改变前后的体积是否发生变化?从以上事实中你得到什么启发?思考??体积相等等高、等截面面积(不受截面形状影响)探究S1祖暅原理 夹在两个平行平面间的两个几何体,被平行于这两个平面的任何平面所截,如果截得的两个截面的面积都相等,那么这两个几何体的体积相等。 S2 我国古代著名数学家祖冲之在计算圆周率等问题方面有光辉的成就。祖冲之的儿子祖暅也在数学上有突出贡献。祖暅在实践的基础上,于5世纪末提出了这个体积计算原理。
祖暅提出这个原理,要比其他国家的数学家早一千多年。在欧洲知道17世纪,才有意大利数学家卡瓦列里(Cavalieri .B,1598年~1647年)提出上述结论 长方体体积:正方体体积:圆柱的体积:圆锥的体积:复习回顾探究:如何解决柱体的体积问题?柱体的体积长方体的体积探究柱体的体积sSS等底等高的柱体体积相等s 以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:柱体体积S’S’ssh锥体的体积等底面积等高的两个锥体的体积相等V柱=shV锥=?探究C′ABCA′B′思考:123探究柱锥关系锥体的体积探究台体的体积棱台(圆台)的体积公式台体体积柱体、锥体、台体的体积公式之间有什么关系?S为底面面积,h为锥体高S分别为上、下底面面积,h 为台体高S为底面面积,h为柱体高三者之间关系解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,即:答:这堆螺帽大约有252个.典型例题各面面积之和总结:空间问题“平面”化棱柱、棱锥、棱台圆柱、圆锥、圆台所用的数学思想:柱体、锥体、台体的表面积柱体、锥体、台体的体积总结数学思想:类比、猜想,特殊到一般,割补,化归与转化作业习题1.3 A组
棱锥的侧面展开图是由三角形组成的平面图形,
棱台的侧面展开图是由梯形组成的平面图形.
这样,求它们的表面积的问题就可转化为求平行四边形、
三角形、梯形的面积问题.棱柱、棱锥、棱台的表面积 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.圆柱的表面积圆柱的侧面展开图是矩形圆锥的表面积圆锥的侧面展开图是扇形圆台的表面积 参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 ?圆台的侧面展开图是扇环三者之间关系 圆柱、圆锥、圆台三者的表面积公式之间有什么关系?12/17/2018例2.一个圆台形花盆盆口直径为20cm,盆底直径为15cm,底部渗水孔直径为1.5cm,盆壁长15cm.为美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆,需要多少油漆.(精确到1毫升,可用计算器) 典型例题花盆外壁的面积=花盆的侧面积+底面积-底面圆孔面积等底等高的三角形面积相等等面积法:温故新知等底面积、等高的两个柱体是否体积相等?类比 取一些书堆放在桌面上(如图所示) ,并改变它们的放置方法,观察改变前后的体积是否发生变化?从以上事实中你得到什么启发?思考??体积相等等高、等截面面积(不受截面形状影响)探究S1祖暅原理 夹在两个平行平面间的两个几何体,被平行于这两个平面的任何平面所截,如果截得的两个截面的面积都相等,那么这两个几何体的体积相等。 S2 我国古代著名数学家祖冲之在计算圆周率等问题方面有光辉的成就。祖冲之的儿子祖暅也在数学上有突出贡献。祖暅在实践的基础上,于5世纪末提出了这个体积计算原理。
祖暅提出这个原理,要比其他国家的数学家早一千多年。在欧洲知道17世纪,才有意大利数学家卡瓦列里(Cavalieri .B,1598年~1647年)提出上述结论 长方体体积:正方体体积:圆柱的体积:圆锥的体积:复习回顾探究:如何解决柱体的体积问题?柱体的体积长方体的体积探究柱体的体积sSS等底等高的柱体体积相等s 以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:柱体体积S’S’ssh锥体的体积等底面积等高的两个锥体的体积相等V柱=shV锥=?探究C′ABCA′B′思考:123探究柱锥关系锥体的体积探究台体的体积棱台(圆台)的体积公式台体体积柱体、锥体、台体的体积公式之间有什么关系?S为底面面积,h为锥体高S分别为上、下底面面积,h 为台体高S为底面面积,h为柱体高三者之间关系解:六角螺帽的体积是六棱柱的体积与圆柱体积之差,即:答:这堆螺帽大约有252个.典型例题各面面积之和总结:空间问题“平面”化棱柱、棱锥、棱台圆柱、圆锥、圆台所用的数学思想:柱体、锥体、台体的表面积柱体、锥体、台体的体积总结数学思想:类比、猜想,特殊到一般,割补,化归与转化作业习题1.3 A组
