4.1 从问题到方程课件（20张PPT）

首先把宇宙万物的所有问题都转化为数学问题；其次，把所有的数学问题转化为代数问题；最后，把所有的代数问题转化为解方程。
一个伟大的设想
解析几何之父:笛卡尔
4.1 从问题到方程
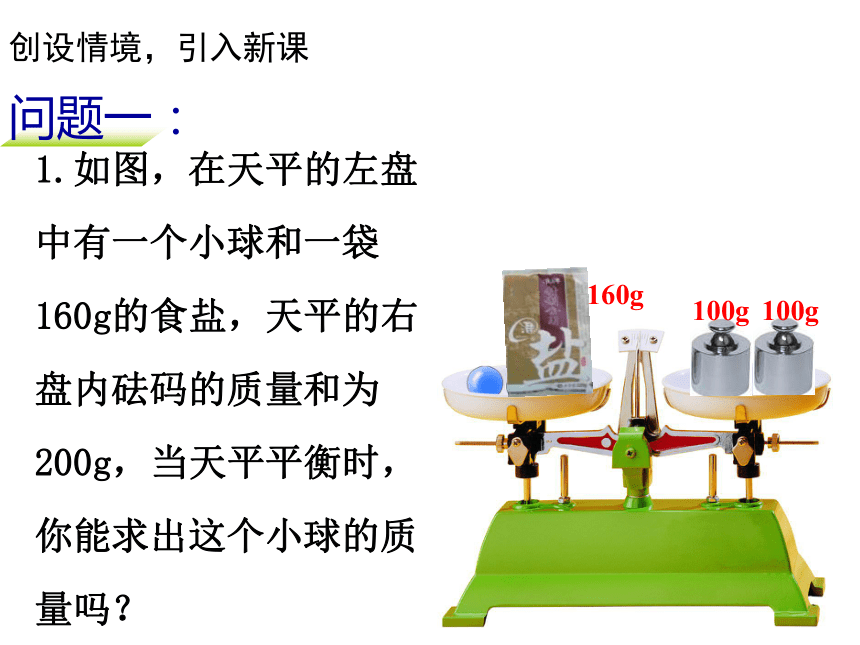
1.如图，在天平的左盘中有一个小球和一袋160g的食盐，天平的右盘内砝码的质量和为200g，当天平平衡时，你能求出这个小球的质量吗？
100g
160g
100g

问题一：
创设情境，引入新课
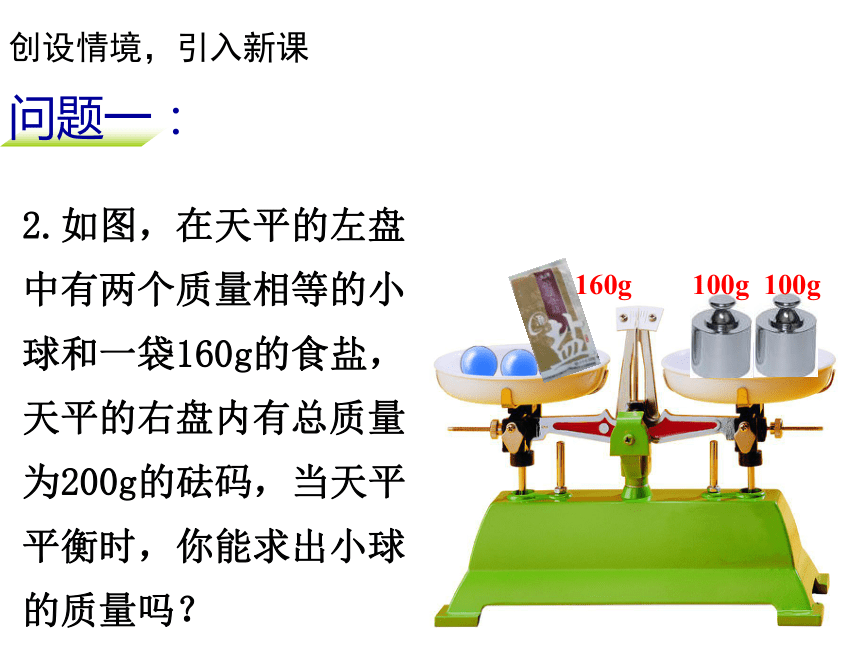
2.如图，在天平的左盘中有两个质量相等的小球和一袋160g的食盐，天平的右盘内有总质量为200g的砝码，当天平平衡时，你能求出小球的质量吗？
100g
160g
100g

问题一：
创设情境，引入新课
100g
160g
100g
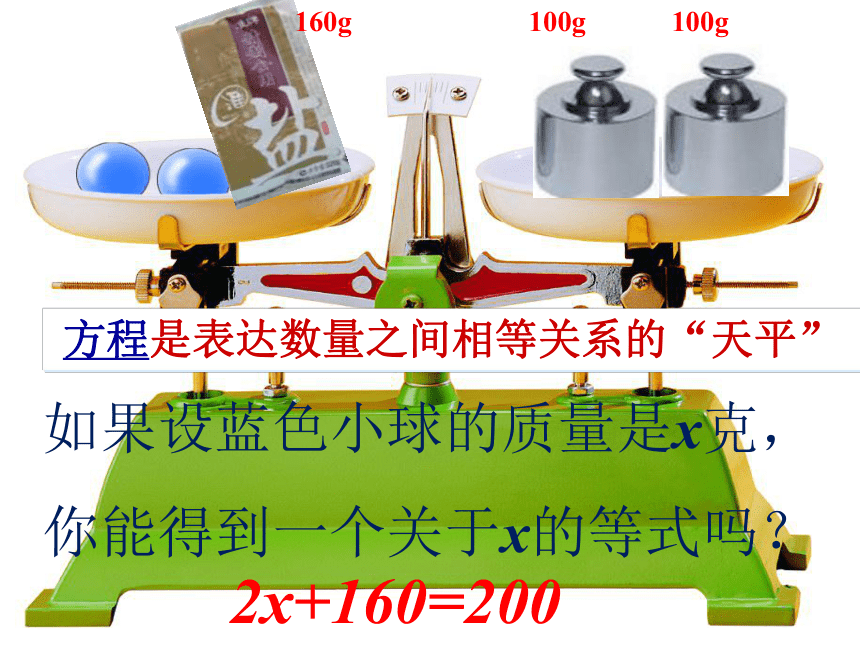
如果设蓝色小球的质量是x克，
你能得到一个关于x的等式吗？
2x+160=200
方程是表达数量之间相等关系的“天平”
问题
篮球联赛规则规定：胜一场得2分，负一场得1分．某篮球队赛了12场，共得20分．怎样描述其中数量之间的相等关系？

某校七年级共有216名师生参加某次活动，要用一辆面包车和几辆客车接送。已知一辆面包车可坐16人，还需要x辆40座的客车.
列出方程_______________
40x+16=216

根据下列问题中的条件列出方程
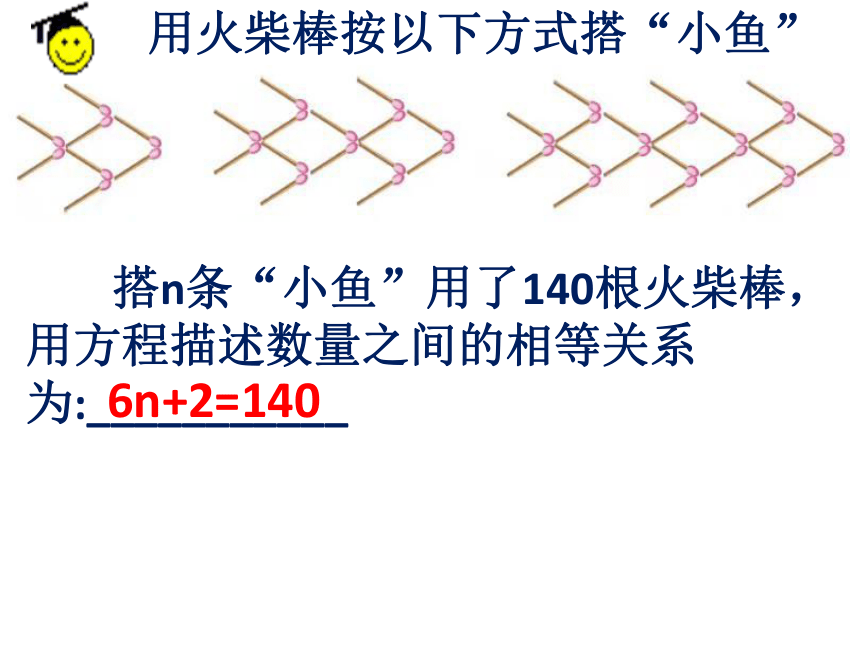
用火柴棒按以下方式搭“小鱼”

搭n条“小鱼”用了140根火柴棒，用方程描述数量之间的相等关系为:___________
6n+2=140
填一填

小红今年5岁，爸爸今年32岁，如果设x年后小红的年龄是爸爸的 ，那么如何用方程来描述数量之间的相等关系?
x年后小红的年龄是_________;
x年后爸爸的年龄是_________.

可得方程:___________________


5+x
32+x
5+x= (32+x)
南京到北京两城市间的铁路经过技术改造后，新开通了D32次动车，列 车在两城市间运行速 度从280千米/时提高到320千米/时，运行时间缩短了1小时. 问两城市间的路程是多少？

根据下列问题中的条件列出方程
设两城市间的路程为x千米，

则原来用的时间为_______小时

现在用的时间为_______小时

可列出方程
。

　　我国古代问题：以绳三折测之，绳多四尺；若将绳四折测之，绳多一尺．绳长、井深各几何？
　　意思是：用绳子量井深，把绳三折来量，井外余绳四尺；把绳四折来量，井外余绳一尺．绳长、井深各几尺？　　

　设绳长为x尺，
那么井深是__________尺或__________尺.
　列出方程为______________________
（1）审题:弄清题目中已知什么，求什么，并找出题目中的等量关系
（2）设未知数为ｘ
（3）用ｘ表示出相关的量，
列出方程.

你觉得“从问题到方程”一般要经历哪些步骤?
体会
议一议:下列方程它们有什么共同特征?
1.方程两边都是整式；
2.方程中只含有 未知数，
并且未知数的指数是 ；
一个
1
只含有一个未知数（元），并且未知数的次数都是1（次）的方程叫做一元一次方程。
1．下列各式中， 一元一次方程是_____
①x＝1 ②3x＋2＝8x－7
③ －2x－3＝0 ④
⑤　　　　　　
练一练



①②③
2．若关于x的方程（k－1）x2＋x－1＝0
是一元一次方程，则k＝ ．

1

讲一讲
通过本节课的学习，你有哪些收获?
古希腊数学家丢番图
被认为是代数学的鼻祖，
但历史上没有一本正式的
著作里留下他完整的生平介绍，甚至连他的国籍都没有明确的记载.
然而有趣的是，他竟然有一个墓志铭。
丢番图的墓志铭
墓中，长眠着一个伟大的人物——丢番图。
他生命的六分之一是幸福的童年.再活十二分之一，颊上长出了细细须.又过了生命的七分之一才结婚.再过5年他感到很幸福，得到了一个儿子.可是这孩子光辉灿烂的生命只有他父亲的一半.儿子死后，老人在悲痛中活了4年，结束了尘世的生涯.
你知道丢番图活了多少岁吗？
走近方程——
你会发觉生活中处处都有她的身影；
你会发现许多令人惊喜的东西；
你会感到自己变得越来越聪明、越来越有本领。许多以前不会解决的问题、不会做的事情，现在都能干得很好！

教师寄语