2018-2019学年度第一学期苏科版九年级数学上册第一章一元二次方程单元检测试卷
文档属性
| 名称 | 2018-2019学年度第一学期苏科版九年级数学上册第一章一元二次方程单元检测试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 30.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-19 00:00:00 | ||
图片预览

文档简介
2018-2019学年度第一学期苏科版九年级数学上册
第一章 一元二次方程 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.关于的一元二次方程的一个根是,则的值为( )
A. B. C.或 D.
?
2.方程的两根之和为( )
A. B. C. D.
?3.下列方程中,一元二次方程的个数有( )
①;②;③;④.
A.个 B.个 C.个 D.个
?4.已知一元二次方程,则下列判断正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.有两个负数根
?5.若是关于的一元二次方程的一根,则值为( )
A. B. C.或 D.
?6.如果关于的方程有实数根、,则的取值范围是( )
A. B.
C. D.
?7.已知一元二次方程的两个解恰好分别是等腰的底边长和腰长,则的周长为( )
A. B.或 C. D.
?8.等腰三角形边长分别为,,,且,是关于的一元二次方程的两根,则的值为
( )
A. B. C.或 D.或
?9.用配方法解方程,配方正确的是( )
A. B.
C. D.
?10.小明家为响应节能减排号召,计划利用两年时间,将家庭每年人均碳排放量由目前的减至.设小明家每年人均碳排放量的平均减少率为,则下面列出的方程中正确的是( )
A. B.
C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )?
11.用公式法解方程,则________;方程的解为________.
?12.两个连续正奇数的积是,则这两个连续正奇数为________.?
13.已知关于的方程的两实根的平方和等于,则的值为________.?
14.已知是方程的一个根,则方程的另一个根是________.
?15.若,则________.
?16.对于正整数、规定关于“*”的新运算:“”,则方程的解为:________.?
17.一元二次方程有两个不相等的实数根,则的取值范围是________.?
18.关于的一元二次方程有两个实数根,则的取值范围是________.?
19.已知关于的一元二次方程的两实数根为,.设,则最小值为________.?
20.已知关于的方程有两个相等的实根,则的值是________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )?
21.用简便的方法解方程:21.
用配方法解方程:.
?
22.已知关于的方程.
若这个方程有实数根,求的取值范围;
若以方程的两个根为横坐标、纵坐标的点恰在反比例函数的图象上,求满足条件的的最小值.
?
23.某商城以元/个的价格从厂家购进一批新款学生文具盒.如果售价为元/个,那么可以卖出这种文具盒个.物价部门限定每个文具盒的售价不得超过进价的.如果该商城卖完这批文具盒赚得元,那么,该商城每个文具盒的售价是多少?这批文具盒共有多少个?
?
24.某公司今年销售一种产品,月份获得利润万元,由于产品畅销,利润逐月增加,月份的利润比月份的利润增加万元,假设该产品利润每月的增长率相同,求这个增长率.
?
25.某商场销售一批名牌服装,平均每天可售出件,每件盈利元,为了增加盈利,商场决定采取适当的降价措施,经调查发现.如果每件服装每降低元,商场平均每天可多售出件.若商场平均每天要盈利元,问每件服装应降价多少元?
?
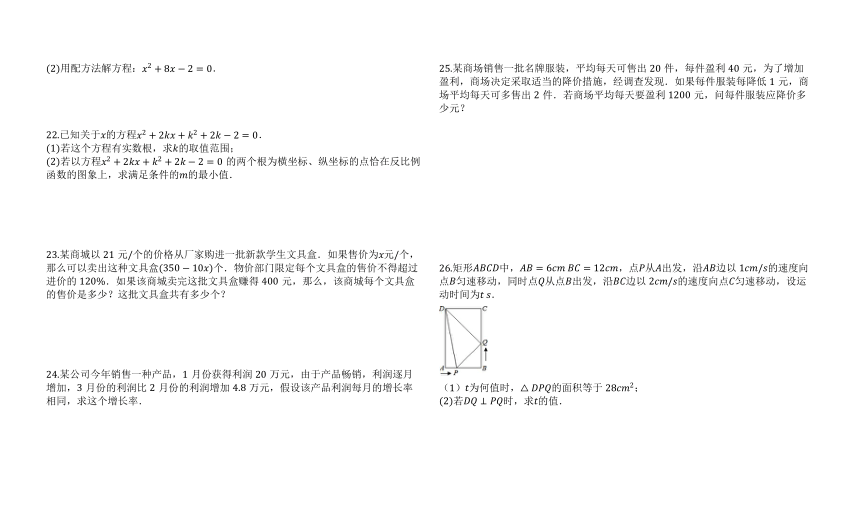
26.矩形中,?,点从出发,沿边以的速度向点匀速移动,同时点从点出发,沿边以的速度向点匀速移动,设运动时间为?.
(1)为何值时,的面积等于;
若时,求的值.
答案
1.B
2.A
3.C
4.A
5.D
6.A
7.A
8.B
9.C
10.C
11.
12.、
13.
14.
15.
16.
17.
18.
19.
20.
21.解:∵,
∴,
∴或,
∴,;∵,
∴,
∴,
∴,
∴,.
22.解:由题意得,
化简得,
解得.设方程的两个根为,,
根据题意得,
又由一元二次方程根与系数的关系得,
那么,
所以,当时,取得最小值.
23.商城每个文具盒的售价是元/个,这批文具盒共有个.
24.这个增长率是.
25.每件服装应降价元.
26.运动秒或秒时,的面积等于;①当与不重合时,
∵,
∴,
∴
∵,
∴,
又∵,
∴,
∴,
∴,
∴解之得:,(舍去)
②当与重合时,此时与重合,可知,
解得;
综上所述,若时,的值为或.
第一章 一元二次方程 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.关于的一元二次方程的一个根是,则的值为( )
A. B. C.或 D.
?
2.方程的两根之和为( )
A. B. C. D.
?3.下列方程中,一元二次方程的个数有( )
①;②;③;④.
A.个 B.个 C.个 D.个
?4.已知一元二次方程,则下列判断正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.有两个负数根
?5.若是关于的一元二次方程的一根,则值为( )
A. B. C.或 D.
?6.如果关于的方程有实数根、,则的取值范围是( )
A. B.
C. D.
?7.已知一元二次方程的两个解恰好分别是等腰的底边长和腰长,则的周长为( )
A. B.或 C. D.
?8.等腰三角形边长分别为,,,且,是关于的一元二次方程的两根,则的值为
( )
A. B. C.或 D.或
?9.用配方法解方程,配方正确的是( )
A. B.
C. D.
?10.小明家为响应节能减排号召,计划利用两年时间,将家庭每年人均碳排放量由目前的减至.设小明家每年人均碳排放量的平均减少率为,则下面列出的方程中正确的是( )
A. B.
C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )?
11.用公式法解方程,则________;方程的解为________.
?12.两个连续正奇数的积是,则这两个连续正奇数为________.?
13.已知关于的方程的两实根的平方和等于,则的值为________.?
14.已知是方程的一个根,则方程的另一个根是________.
?15.若,则________.
?16.对于正整数、规定关于“*”的新运算:“”,则方程的解为:________.?
17.一元二次方程有两个不相等的实数根,则的取值范围是________.?
18.关于的一元二次方程有两个实数根,则的取值范围是________.?
19.已知关于的一元二次方程的两实数根为,.设,则最小值为________.?
20.已知关于的方程有两个相等的实根,则的值是________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )?
21.用简便的方法解方程:21.
用配方法解方程:.
?
22.已知关于的方程.
若这个方程有实数根,求的取值范围;
若以方程的两个根为横坐标、纵坐标的点恰在反比例函数的图象上,求满足条件的的最小值.
?
23.某商城以元/个的价格从厂家购进一批新款学生文具盒.如果售价为元/个,那么可以卖出这种文具盒个.物价部门限定每个文具盒的售价不得超过进价的.如果该商城卖完这批文具盒赚得元,那么,该商城每个文具盒的售价是多少?这批文具盒共有多少个?
?
24.某公司今年销售一种产品,月份获得利润万元,由于产品畅销,利润逐月增加,月份的利润比月份的利润增加万元,假设该产品利润每月的增长率相同,求这个增长率.
?
25.某商场销售一批名牌服装,平均每天可售出件,每件盈利元,为了增加盈利,商场决定采取适当的降价措施,经调查发现.如果每件服装每降低元,商场平均每天可多售出件.若商场平均每天要盈利元,问每件服装应降价多少元?
?
26.矩形中,?,点从出发,沿边以的速度向点匀速移动,同时点从点出发,沿边以的速度向点匀速移动,设运动时间为?.
(1)为何值时,的面积等于;
若时,求的值.
答案
1.B
2.A
3.C
4.A
5.D
6.A
7.A
8.B
9.C
10.C
11.
12.、
13.
14.
15.
16.
17.
18.
19.
20.
21.解:∵,
∴,
∴或,
∴,;∵,
∴,
∴,
∴,
∴,.
22.解:由题意得,
化简得,
解得.设方程的两个根为,,
根据题意得,
又由一元二次方程根与系数的关系得,
那么,
所以,当时,取得最小值.
23.商城每个文具盒的售价是元/个,这批文具盒共有个.
24.这个增长率是.
25.每件服装应降价元.
26.运动秒或秒时,的面积等于;①当与不重合时,
∵,
∴,
∴
∵,
∴,
又∵,
∴,
∴,
∴,
∴解之得:,(舍去)
②当与重合时,此时与重合,可知,
解得;
综上所述,若时,的值为或.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
