江苏省海安县2019届高三上学期期中质量监测数学试题(小题解析)
文档属性
| 名称 | 江苏省海安县2019届高三上学期期中质量监测数学试题(小题解析) |  | |
| 格式 | zip | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-19 12:47:26 | ||
图片预览



文档简介
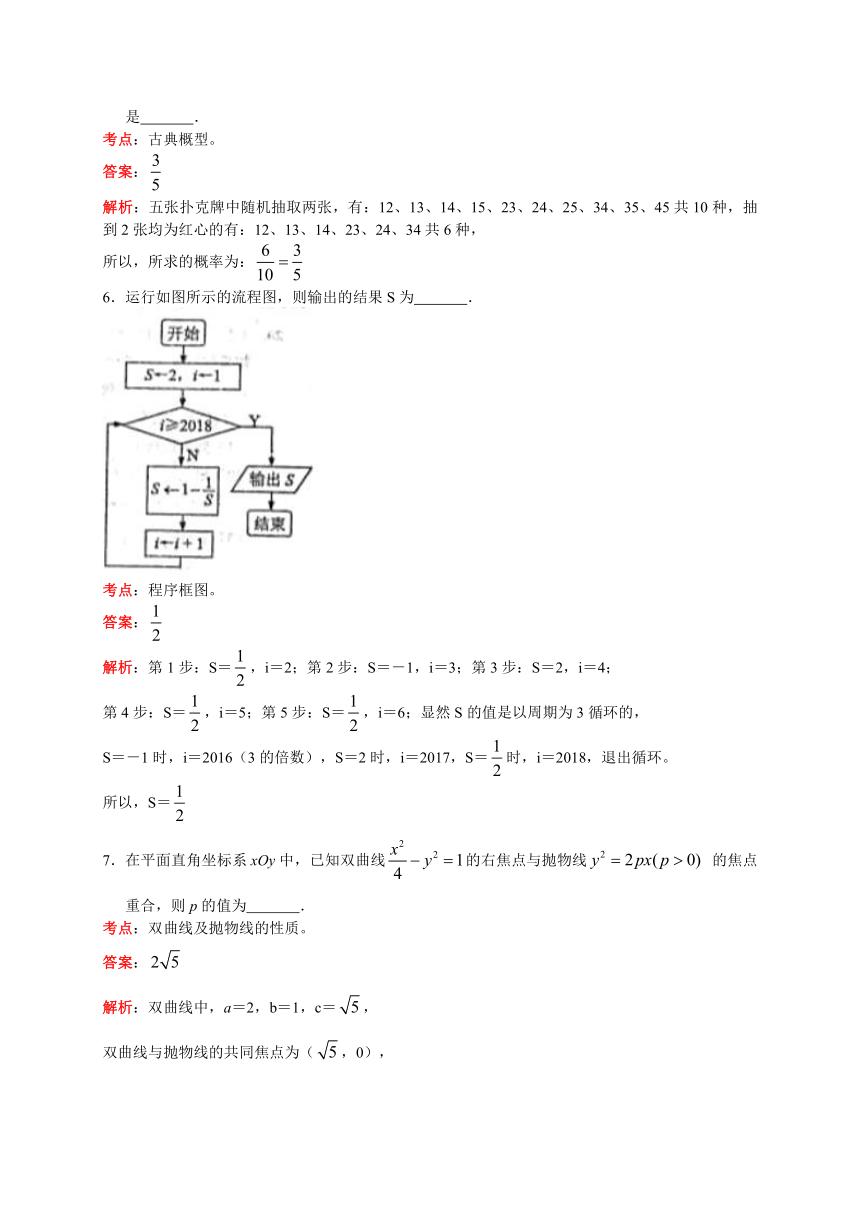
2019届高三期中学业质量监测试题
数 学2018.11
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.)
1.已知全集U={0,2,4,6,8},集合A={0,4,6},则?UA= .
考点:集合的运算。
答案:{2,8}
解析:在全集U中找出集合A中没有的元素就是答案,所以,?UA={2,8}
2.已知复数z满足(i为虚数单位),则复数z的模为 .
考点:复数的相关概念及其运算。
答案:
解析:Z=,
所以,复数z的模为:
3.已知某民营车企生产A,B,C三种型号的新能源汽车,库存台数依次为120,210,150,某安检单位欲从中用分层抽样的方法随机抽取16台车进行安全测试,则应抽取B型号的新能源汽车的台数为 .
考点:分层抽样方法。
答案:7
解析:抽取的比例为:,所以,抽取B型号台数为:=7
4.设实数x,y满足,则x+y的最小值为
考点:线性规划。
答案:2
解析:不等式组所表示的平面区域如图所示,当目标函数z=x+y经过点B(1,1)时,
x+y有最小值为:1+1=2,
5.有红心1,2,3,4和黑桃5这五张扑克牌,现从中随机抽取两张,则抽到的牌均为红心的概率是 .
考点:古典概型。
答案:
解析:五张扑克牌中随机抽取两张,有:12、13、14、15、23、24、25、34、35、45共10种,抽到2张均为红心的有:12、13、14、23、24、34共6种,
所以,所求的概率为:
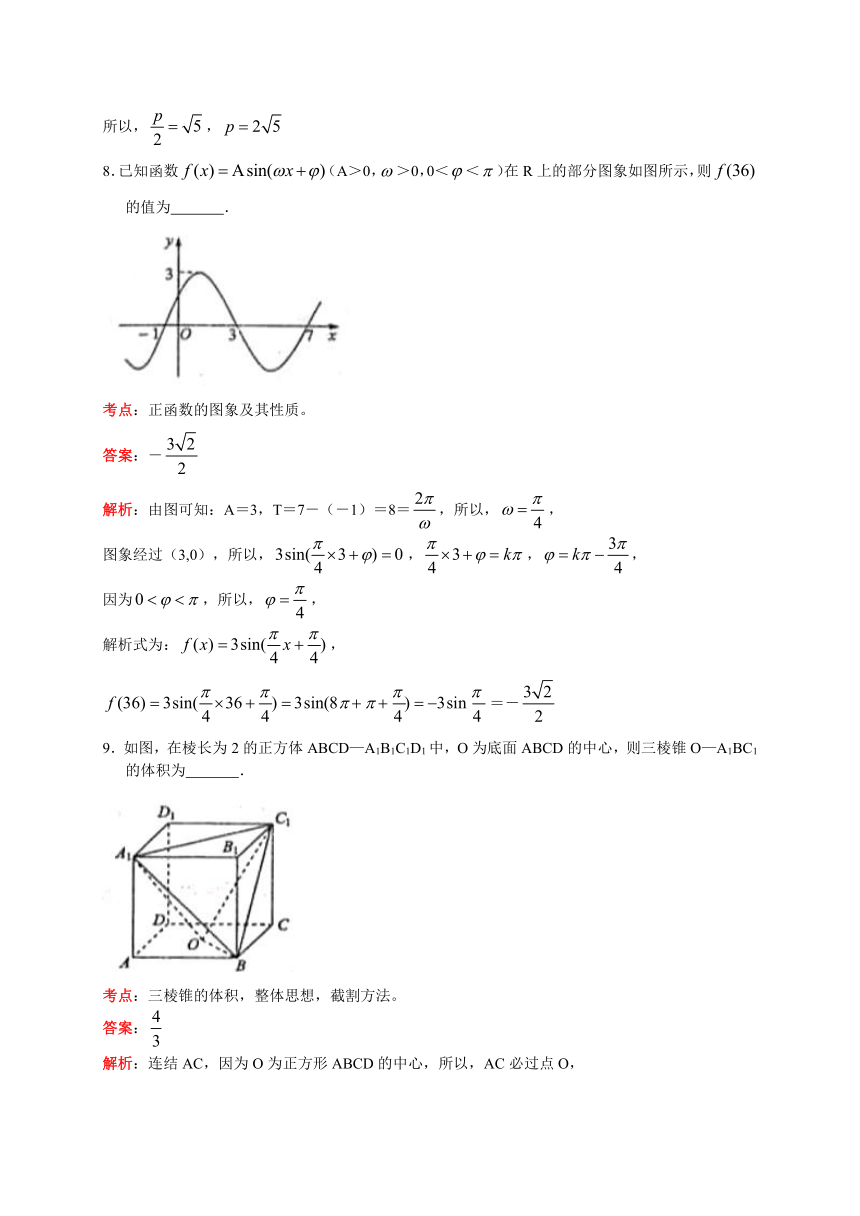
6.运行如图所示的流程图,则输出的结果S为 .
考点:程序框图。
答案:
解析:第1步:S=,i=2;第2步:S=-1,i=3;第3步:S=2,i=4;
第4步:S=,i=5;第5步:S=,i=6;显然S的值是以周期为3循环的,
S=-1时,i=2016(3的倍数),S=2时,i=2017,S=时,i=2018,退出循环。
所以,S=
7.在平面直角坐标系xOy中,已知双曲线的右焦点与抛物线 的焦点重合,则p的值为 .
考点:双曲线及抛物线的性质。
答案:
解析:双曲线中,a=2,b=1,c=,
双曲线与抛物线的共同焦点为(,0),
所以,,
8.已知函数(A>0,>0,0<<)在R上的部分图象如图所示,则的值为 .
考点:正函数的图象及其性质。
答案:-
解析:由图可知:A=3,T=7-(-1)=8=,所以,,
图象经过(3,0),所以,,,,
因为,所以,,
解析式为:,
=-
9.如图,在棱长为2的正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,则三棱锥O—A1BC1的体积为 .
考点:三棱锥的体积,整体思想,截割方法。
答案:
解析:连结AC,因为O为正方形ABCD的中心,所以,AC必过点O,
VO—A1BC1=V正方形AC1-VA1-ABO-VC1-CBO-VA1-BB1C1
=×8-××××2×2-××2×2×2
=4--=
10.设等比数列的公比为q(0<q<1),前n项和为.若存在,使得,且,则m的值为 .
考点:等秕数列的通项公式,前n项和公式。
答案:9
解析:由,得:,即,
因为0
所以,m=9
11.已知AB为圆的直径,点C,D为圆上两点(在AB两侧),且AC=1,AD=2,
AB=3,则的值为 .
考点:平面向量的三角形法则,数量积,余弦定理。
答案:-
解析:连结BD,因为AB为直径,所以,∠C=∠D=90?,
所以,BD=,BC=,
cos∠DAB=,cos∠CAB=,
cos∠CAD=cos(∠CAB+∠DAB)==,
==2×1×-2×3×
=-
12.已知函数为奇函数,则不等式的解集为 .
考点:奇函数的性质,对数函数的性质,分式不等式化为一元二次不等式的方法。
答案:(-∞,-1)∪(3,+∞)
解析:依题意,有:,即
=,
所以,即:,所以,k=±1,
当k=1时,没有意义,舍去,所以,k=-1
,不等式即为:<1=
所以,0<<2,
由>0,得:x<-1或x>1,
由<2,即<0,即>0,得:x<1或x>3,
综上可得:x<-1或x>3,所以,解集为:(-∞,-1)∪(3,+∞)
13.已知正数x,y,z满足,且z≤3x,则P=的取值范围是 .
考点:换元法,一元二次不等式,函数的导数及其应用。
答案:
解析:化为:,又z≤3x,
所以,,去分母,合并同类项,得:,
即,即,
所以,,即,令t=,则,
P===,令,
=0,得:,
t () (,1)
- 0 +
↘ ↗
所以,当时,P有最小值为:=,
,,即P有最大值,
所以,P的取值范围是
14.设命题p:“存在[1,2],使得,其中a,b,cR.”若无论a,b取何值时,命题p都是真命题,则c的最大值为 .
考点:绝对值不等式,常用逻辑用语,分析问题解决问题的能力。
答案:
解析:
二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.)
15.(本小题满分14分)
已知a,b,c分别是△ABC的三个内角A,B,C的对边,若平面向量,,,,且∥.
(1)求cosA的值;
(2)若tanB=,求角C的大小.
16.(本小题满分14分)
如图,在四棱锥P—ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC,PB=PD=AC,E是PD的中点,求证:
(1)PB∥平面ACE;
(2)平面PAC⊥平面ABCD.
17.(本小题满分14分)
如图,已知AB为椭圆E:(a>b>0)的长轴,过坐标原点O且倾斜角为135°的直线交椭圆E于C,D两点,且D在x轴上的射影D'恰为椭圆E的长半轴OB的中点.
(1)求椭圆E的离心率;
(2)若AB=8,不过第四象限的直线l与椭圆E和以CD为直径的圆均相切,求直线l的方程.
18.(本小题满分16分)
某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族S中的成员仅以自驾或骑单车方式通勤.分析显示:当S中x%(0<x<100)的成员自驾时,自驾群体的人均通勤时间为(单位:分钟),而骑单车群体的人均通勤时间为(单位:分钟).试根据上述分析结果回答下列问题:
(1)试确定x的取值范围,使得自驾群体的人均通勤时间少于骑单车群体的人均通勤时间;
(2)求该地上班族S的人均通勤时间的表达式,讨论的单调性,并说明其实际意义.
19.(本小题满分16分)
已知函数,,.
(1)求函数的极值点;
(2)已知T(,)为函数,的公共点,且函数,在点T处的切线相同,求a的值;
(3)若函数在(0,)上的零点个数为2,求a的取值范围.
20.(本小题满分16分)
如果数列,,…,(m≥3,)满足:①<<…<;②存在实数,,,…,和d,使得≤<≤<≤<…≤<,且对任意0≤i≤m﹣1(i),均有,那么称数列,,…,是“Q数列”.
(1)判断数列1,3,6,10是不是“Q数列”,并说明理由;
(2)已知k,t均为常数,且k>0,求证:对任意给定的不小于3的正整数m,数列(n=1,2,…,m)都是“Q数列”;
(3)若数列(n=1,2,…,m)是“Q数列”,求m的所有可能值.
参考答案
15.
16.
17.
18.
19.
20.
同课章节目录
