2018年高中数学北师大版必修2课件:第一章立体几何初步1-3-2由三视图还原成实物图课件(41张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-3-2由三视图还原成实物图课件(41张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-19 00:00:00 | ||
图片预览









文档简介
课件41张PPT。由三视图还原成实物图欣赏三视图你认识它吗?问题一:如果要做一个水管的三叉接头,工人事先看到的不是图1,而是图2,你能替这位工人师傅根据这三个图形制造出水管接头吗?
若已知一个几何体的三视图,我们如何去想象这个几何体的原形结构,并画出其示意图呢?
图1复习回顾:
一、三视图:
1、从正面看到的图形叫做主视图;从左面看到的图形叫左视图;从上面看到的图形叫俯视图。这三张图,称为三视图.
2、形体可见轮廓线画粗实线,不可见轮廓线画虚线
二、三视图的对应规律:俯视图和左视图主视图和俯视图主视图和左视图----长对正----高平齐----宽相等可注意哦三、 基本几何体的三视图(1)正方体的三视图都是———(2)圆柱的三视图中有两个是———
另一个是—— (3)圆锥的三视图中有两个是———,另
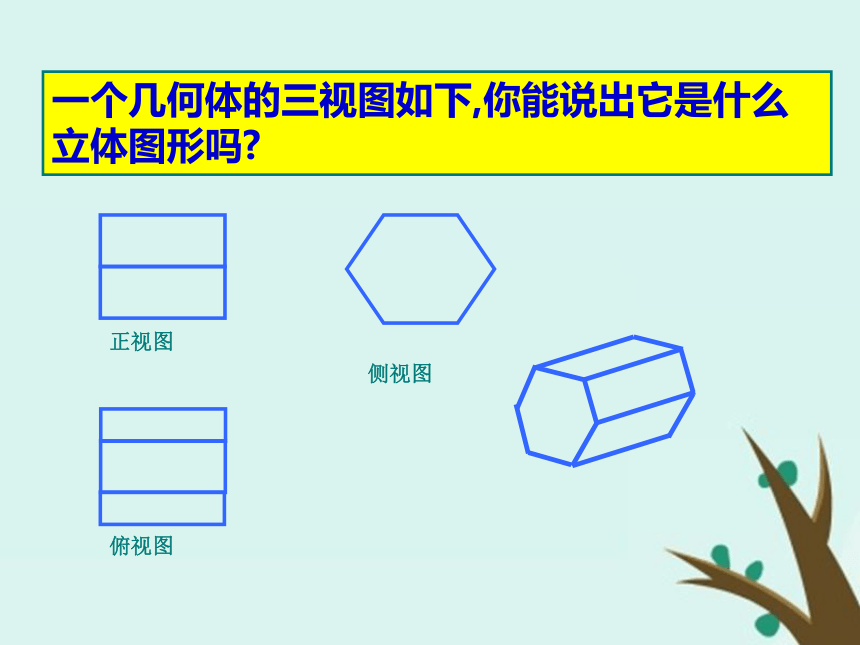
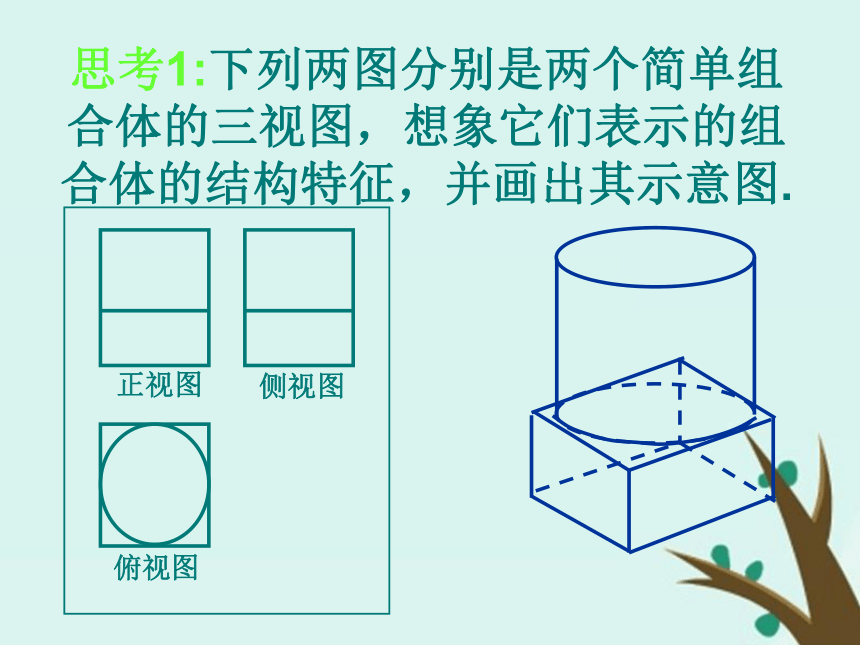
一个是—————。(4)球的三视图都是——正方形长方形圆三角形圆和一个点圆请找出下列三视图对应的几何体AbcaBC第 一 组eEFGfg第 二 组长方体一个几何体的三视图如下,你能说出它是什么立体图形吗? 与上一张三视图有何区别与联系?思考1:下列两图分别是两个简单组合体的三视图,想象它们表示的组合体的结构特征,并画出其示意图. 思考2:下列两图分别是两个简单组合体的三视图,想象它们表示的组合体的结构特征,并作适当描述.
六棱锥与六棱柱的组合体举重杠铃1、下图中的三视图表示哪个几何体?变式训练一:2、如图是一个物体的三视图,试说出物体
的形状。正视图
侧视图俯视图3、一空间几何体的三视图如图所示,则该几何体是___2 正视图 2例2说出下面的三视图表示的几何体的结构特征,并画出其示意图.将一个长方体挖去两个
小长方体后剩余的部分例 3 一个几何体的三视图如图所示,其中正视图和左视图是腰长为6的两个全等的等腰直角三角形.用多少个这样的几何体可以拼成一个棱长为6的正方体. 该几何体为四棱锥D1—ABCD 正视图:等腰直角三角形;
左视图:等腰直角三角形;
俯视图:正方形(要加对角线BD哟)
要三个这样的几何体才能拼成正方体,分别
四棱锥 、四棱锥 、
四棱锥
1.一个零件的主视图和俯视图如图,请描述这个零件的形状,并补画出它的左视图.
主视图俯视图球的一部分与圆柱的组合体,左视图同主视图.
变式训练二:2、说出下面的三视图表示的几何体的结构特征 问题二:已知物体三视图的外轮廓,如何构思该物体?与同学交流你的看法和具体做法.构思过程:课堂活动螺丝杆高考题欣赏(共10道)1、(全国新课标文)(8)在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为
D2、(浙江文)(7)几何体的三视图如图所示,则这个几何体的直观图可以是
【答案】B3、北京文)(5)某四棱锥的三视图如图所示,该四棱锥的表面积是
(A)32 (B)16+(C)48 (D)【解析】:由三视图可知几何体为底面边长为4,高为2的正四棱锥,则四棱锥的斜高为,表面积故选B。4、(广东文9)
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为A.B.C. D.该几何体是一个底面为菱形的四棱锥,, 则该几何体的体积 √5、(陕西文)5.某几何体的三视图如图所示,则它的体积是( )
B.
C.8-2π【解】选A 由几何体的三视图可知几何体为一个组合体,即一个正方体中间去掉一个圆锥体,所以它的体积是
.
A.D.6、一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是 A.3 B. C.2 D.
解析:由三视图得空间几何体为倒放着的直三棱柱,底面为直角三角形,答案:D7、一个棱锥的三视图如图,则该棱锥的全面积为8、已知四棱锥P-ABCD的三视图如图所示.
[答案] C 9、(文)如下图中的三个直角三角形是一个体积20cm3的几何体的三视图,则h=________ cm.
[答案] 410、如何把组合体的三视图还原成几何体的实形
1、把每个视图分解为基本图形(三角形,圆等)
2、结合对应部分的三视图想象对应的基本几何体
3、结合虚实线概括组合体课堂小结.
课外思考题
用小方块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗?它至少需要多少个小立方块?最多需要多少个小立方块?分别画出它们的几何体的左视图.主视图 俯视图主视图 俯视图左视图主视图 俯视图左视图主视图 俯视图
若已知一个几何体的三视图,我们如何去想象这个几何体的原形结构,并画出其示意图呢?
图1复习回顾:
一、三视图:
1、从正面看到的图形叫做主视图;从左面看到的图形叫左视图;从上面看到的图形叫俯视图。这三张图,称为三视图.
2、形体可见轮廓线画粗实线,不可见轮廓线画虚线
二、三视图的对应规律:俯视图和左视图主视图和俯视图主视图和左视图----长对正----高平齐----宽相等可注意哦三、 基本几何体的三视图(1)正方体的三视图都是———(2)圆柱的三视图中有两个是———
另一个是—— (3)圆锥的三视图中有两个是———,另
一个是—————。(4)球的三视图都是——正方形长方形圆三角形圆和一个点圆请找出下列三视图对应的几何体AbcaBC第 一 组eEFGfg第 二 组长方体一个几何体的三视图如下,你能说出它是什么立体图形吗? 与上一张三视图有何区别与联系?思考1:下列两图分别是两个简单组合体的三视图,想象它们表示的组合体的结构特征,并画出其示意图. 思考2:下列两图分别是两个简单组合体的三视图,想象它们表示的组合体的结构特征,并作适当描述.
六棱锥与六棱柱的组合体举重杠铃1、下图中的三视图表示哪个几何体?变式训练一:2、如图是一个物体的三视图,试说出物体
的形状。正视图
侧视图俯视图3、一空间几何体的三视图如图所示,则该几何体是___2 正视图 2例2说出下面的三视图表示的几何体的结构特征,并画出其示意图.将一个长方体挖去两个
小长方体后剩余的部分例 3 一个几何体的三视图如图所示,其中正视图和左视图是腰长为6的两个全等的等腰直角三角形.用多少个这样的几何体可以拼成一个棱长为6的正方体. 该几何体为四棱锥D1—ABCD 正视图:等腰直角三角形;
左视图:等腰直角三角形;
俯视图:正方形(要加对角线BD哟)
要三个这样的几何体才能拼成正方体,分别
四棱锥 、四棱锥 、
四棱锥
1.一个零件的主视图和俯视图如图,请描述这个零件的形状,并补画出它的左视图.
主视图俯视图球的一部分与圆柱的组合体,左视图同主视图.
变式训练二:2、说出下面的三视图表示的几何体的结构特征 问题二:已知物体三视图的外轮廓,如何构思该物体?与同学交流你的看法和具体做法.构思过程:课堂活动螺丝杆高考题欣赏(共10道)1、(全国新课标文)(8)在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为
D2、(浙江文)(7)几何体的三视图如图所示,则这个几何体的直观图可以是
【答案】B3、北京文)(5)某四棱锥的三视图如图所示,该四棱锥的表面积是
(A)32 (B)16+(C)48 (D)【解析】:由三视图可知几何体为底面边长为4,高为2的正四棱锥,则四棱锥的斜高为,表面积故选B。4、(广东文9)
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为A.B.C. D.该几何体是一个底面为菱形的四棱锥,, 则该几何体的体积 √5、(陕西文)5.某几何体的三视图如图所示,则它的体积是( )
B.
C.8-2π【解】选A 由几何体的三视图可知几何体为一个组合体,即一个正方体中间去掉一个圆锥体,所以它的体积是
.
A.D.6、一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积是 A.3 B. C.2 D.
解析:由三视图得空间几何体为倒放着的直三棱柱,底面为直角三角形,答案:D7、一个棱锥的三视图如图,则该棱锥的全面积为8、已知四棱锥P-ABCD的三视图如图所示.
[答案] C 9、(文)如下图中的三个直角三角形是一个体积20cm3的几何体的三视图,则h=________ cm.
[答案] 410、如何把组合体的三视图还原成几何体的实形
1、把每个视图分解为基本图形(三角形,圆等)
2、结合对应部分的三视图想象对应的基本几何体
3、结合虚实线概括组合体课堂小结.
课外思考题
用小方块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗?它至少需要多少个小立方块?最多需要多少个小立方块?分别画出它们的几何体的左视图.主视图 俯视图主视图 俯视图左视图主视图 俯视图左视图主视图 俯视图
