2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-2平行关系的性质课件(16张)
文档属性
| 名称 | 2018年高中数学北师大版必修2课件:第一章立体几何初步1-5-2平行关系的性质课件(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 963.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-19 12:52:49 | ||
图片预览



文档简介
课件16张PPT。平 行 关 系 的 性 质1.直线与平面
平行的判定:定义法:判定定理法:2.两个平面平
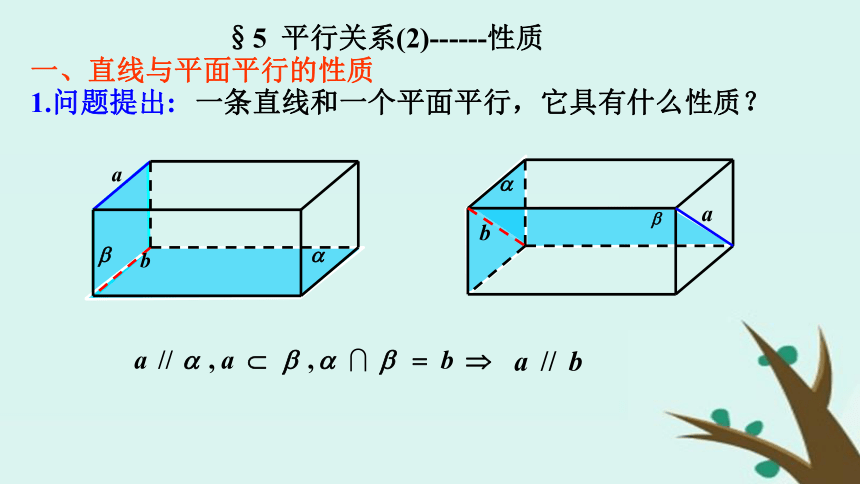
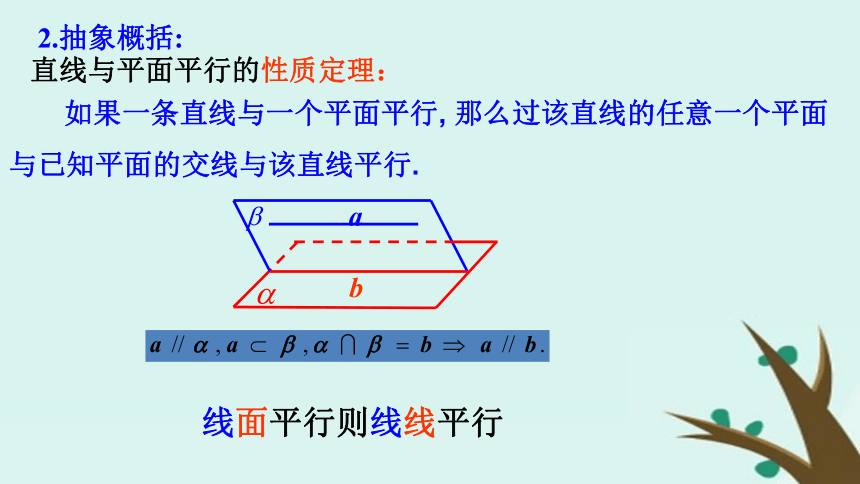
行的判定:(线面平行证面面平行)定义法判定定理法(线线平行证线面平行)复习回顾§5 平行关系(2)------性质一、直线与平面平行的性质1.问题提出:一条直线和一个平面平行,它具有什么性质?证明:2.抽象概括:直线与平面平行的性质定理: 如果一条直线与一个平面平行, 那么过该直线的任意一个平面
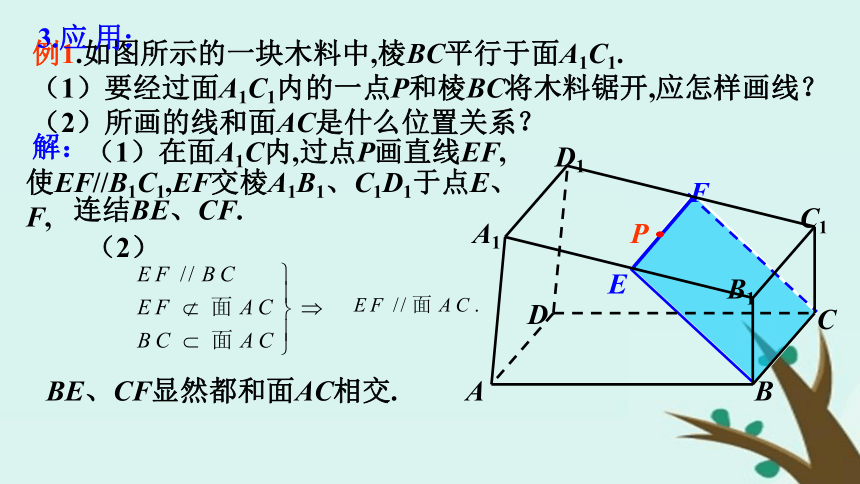
与已知平面的交线与该直线平行.线面平行则线线平行例1.如图所示的一块木料中,棱BC平行于面A1C1.
(1)要经过面A1C1内的一点P和棱BC将木料锯开,应怎样画线?
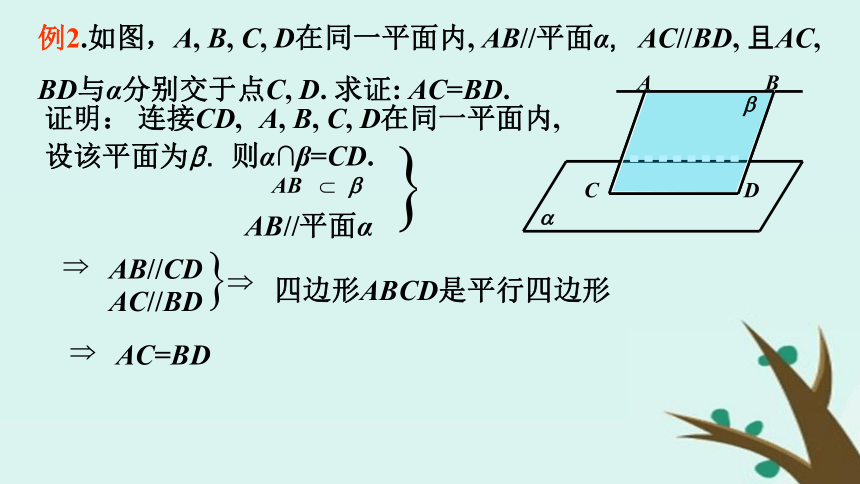
(2)所画的线和面AC是什么位置关系?解:(1)在面A1C内,过点P画直线EF,使EF//B1C1,EF交棱A1B1、C1D1于点E、F,连结BE、CF.(2)BE、CF显然都和面AC相交.3.应 用:例2.如图,A, B, C, D在同一平面内, AB//平面α,AC//BD, 且AC,
BD与α分别交于点C, D. 求证: AC=BD.证明:连接CD,A, B, C, D在同一平面内,设该平面为β.则α∩β=CD.AB//平面αAB//CDAC//BD四边形ABCD是平行四边形AC=BD二、两个平面平行的性质1.问题提出:两个平面平行,它具有什么性质?证明:另证:2.抽象概括:平面与平面平行的性质定理: 如果两个平行平面同时和第三个平面相交, 那么它们
的交线平行.(面面平行证线线平行)3.应 用:例3.如图, 直线a和b分别交 、 、 于点A、B、C和点D、E、F.
求证: 例3.如图, 直线a和b分别交 、 、 于点A、B、C和点D、E、F.
求证: 证明:连接AF,交平面 于点G.平面ADF∩α=AD平面ADF∩β=GE平面ACF∩β=BG平面ACF∩γ=CF思考:若DE=6, EF=2, BC=3. 则AB=________.9三、反馈练习1.如果直线a//α, 直线b , 那么a与b一定平行吗?为什么?2.如果直线a//直线 b , 且a//α , 那么b与α的位置关系是( )
A. 相交 B. b//a C. D. b//a 或D3.已知两条直线m, n及平面α, 判断下面四个命题是否正确:
(1)若m//α, n//α, 则m//n;
(2)若m//α, m//n, 则n//α;
(3)若m//α, 则m平行α内所有直线;
(4)若m平行于α内无数条直线, 则m//α .4.如果一条直线与两个平行平面中的一个平行,那么这条直线
与另一个平面的位置关系是( )
A. 平行 B. 相交
C. 在平面内 D. 平行或在平面内D5.如果三个平面把空间分成4个部分,那么这个平面有怎样的位
置关系?如果3个平面把空间分成6个部分,那么这3个平面有
怎样的位置关系?四、课堂小结1.直线与平面
平行的性质:定义法:性质定理法:2.两个平面平
行的性质:(面面平行证线线平行)定义法性质定理法(线面平行证线线平行)
平行的判定:定义法:判定定理法:2.两个平面平
行的判定:(线面平行证面面平行)定义法判定定理法(线线平行证线面平行)复习回顾§5 平行关系(2)------性质一、直线与平面平行的性质1.问题提出:一条直线和一个平面平行,它具有什么性质?证明:2.抽象概括:直线与平面平行的性质定理: 如果一条直线与一个平面平行, 那么过该直线的任意一个平面
与已知平面的交线与该直线平行.线面平行则线线平行例1.如图所示的一块木料中,棱BC平行于面A1C1.
(1)要经过面A1C1内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线和面AC是什么位置关系?解:(1)在面A1C内,过点P画直线EF,使EF//B1C1,EF交棱A1B1、C1D1于点E、F,连结BE、CF.(2)BE、CF显然都和面AC相交.3.应 用:例2.如图,A, B, C, D在同一平面内, AB//平面α,AC//BD, 且AC,
BD与α分别交于点C, D. 求证: AC=BD.证明:连接CD,A, B, C, D在同一平面内,设该平面为β.则α∩β=CD.AB//平面αAB//CDAC//BD四边形ABCD是平行四边形AC=BD二、两个平面平行的性质1.问题提出:两个平面平行,它具有什么性质?证明:另证:2.抽象概括:平面与平面平行的性质定理: 如果两个平行平面同时和第三个平面相交, 那么它们
的交线平行.(面面平行证线线平行)3.应 用:例3.如图, 直线a和b分别交 、 、 于点A、B、C和点D、E、F.
求证: 例3.如图, 直线a和b分别交 、 、 于点A、B、C和点D、E、F.
求证: 证明:连接AF,交平面 于点G.平面ADF∩α=AD平面ADF∩β=GE平面ACF∩β=BG平面ACF∩γ=CF思考:若DE=6, EF=2, BC=3. 则AB=________.9三、反馈练习1.如果直线a//α, 直线b , 那么a与b一定平行吗?为什么?2.如果直线a//直线 b , 且a//α , 那么b与α的位置关系是( )
A. 相交 B. b//a C. D. b//a 或D3.已知两条直线m, n及平面α, 判断下面四个命题是否正确:
(1)若m//α, n//α, 则m//n;
(2)若m//α, m//n, 则n//α;
(3)若m//α, 则m平行α内所有直线;
(4)若m平行于α内无数条直线, 则m//α .4.如果一条直线与两个平行平面中的一个平行,那么这条直线
与另一个平面的位置关系是( )
A. 平行 B. 相交
C. 在平面内 D. 平行或在平面内D5.如果三个平面把空间分成4个部分,那么这个平面有怎样的位
置关系?如果3个平面把空间分成6个部分,那么这3个平面有
怎样的位置关系?四、课堂小结1.直线与平面
平行的性质:定义法:性质定理法:2.两个平面平
行的性质:(面面平行证线线平行)定义法性质定理法(线面平行证线线平行)
