【专题突破训练】北师大九年级下第三章圆单元测试卷(有答案)
文档属性
| 名称 | 【专题突破训练】北师大九年级下第三章圆单元测试卷(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-19 00:00:00 | ||
图片预览




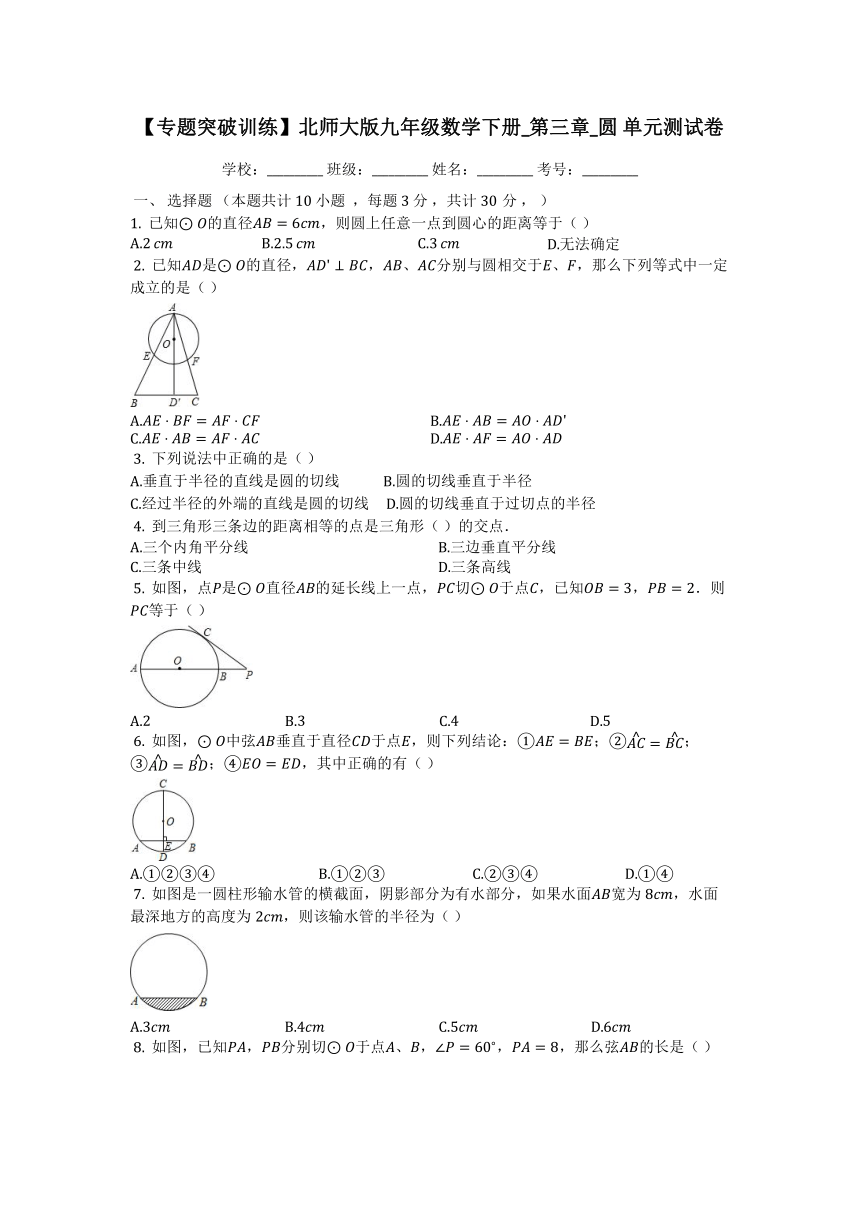
文档简介
【专题突破训练】北师大版九年级数学下册_第三章_圆 单元测试卷
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 已知⊙??的直径????=6????,则圆上任意一点到圆心的距离等于( )
A.2?????
B.2.5?????
C.3?????
D.无法确定
?2. 已知????是⊙??的直径,????′⊥????,????、????分别与圆相交于??、??,那么下列等式中一定成立的是( )
/
A.?????????=?????????
B.?????????=?????????′
C.?????????=?????????
D.?????????=?????????
?3. 下列说法中正确的是( )
A.垂直于半径的直线是圆的切线 B.圆的切线垂直于半径
C.经过半径的外端的直线是圆的切线 D.圆的切线垂直于过切点的半径
?4. 到三角形三条边的距离相等的点是三角形( )的交点.
A.三个内角平分线
B.三边垂直平分线
C.三条中线
D.三条高线
?5. 如图,点??是⊙??直径????的延长线上一点,????切⊙??于点??,已知????=3,????=2.则????等于( )
/
A.2
B.3
C.4
D.5
?6. 如图,⊙??中弦????垂直于直径????于点??,则下列结论:①????=????;②
????
=
????
;③
????
=
????
;④????=????,其中正确的有( )
/
A.①②③④
B.①②③
C.②③④
D.①④
?7. 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面????宽为8????,水面最深地方的高度为2????,则该输水管的半径为( )
/
A.3????
B.4????
C.5????
D.6????
?8. 如图,已知????,????分别切⊙??于点??、??,∠??=
60
°
,????=8,那么弦????的长是( )
/
A.4
B.8
C.4
3
D.8
3
?9. 有一边长为2
3
的正三角形,则它的外接圆的面积为( )
A.2
3
??
B.4
3
??
C.4??
D.12??
?10. 如图,已知????是⊙??的直径,??是⊙??上的点,sin??=
1
4
,????=1,则⊙??的半径等于( )
/
A.4
B.3
C.2
D.
15
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 一个扇形的弧长是38??????,面积是190????
??
2
,这个扇形的半径是________????.
?12. 如图,已知四边形????????内接于⊙??,∠??????=
60
°
,则∠??????的度数是________.
////
第12题 第13题 第14题 第15题
?13. 如图,在⊙??中,弦????与????相交于点??,已知????=3????,????=4????,????=2????,那么????=________????.
?14. 如图????是⊙??的直径,∠??????=
42
°
,点??是弦????的中点,则∠??????的度数是________度.
?15. 如图,????是⊙??的直径,????是垂直于????的弦,垂足为??,已知????=10,????=9,则????=________.
?16. 平面上的一点和⊙??的最近点距离为4????,最远距离为10????,则这圆的半径是________????.
?17. 如图,在⊙O中,OB为半径,AB是⊙O的切线,OA与⊙O相交于点C,∠A=30°,OA=8,则阴影部分的面积是________. / / / /
第17题图 第18题 第19题 第20题
?18. 如图,⊙??是△??????的外接圆,????是⊙??的直径,若⊙??的半径为
3
2
,????=2,sin??的值是________.
19. 如图,摩天轮⊙??的最高处??到地面??的距离是82米,最低处??到地面??的距离是2米.若游客从??处乘摩天轮绕一周需12分钟,则游客从??处乘摩天轮到地面??的距离是62米时最少需________分钟.
?20. 如图,点??、??、??在⊙??上,若∠??????=
24
°
,则∠??????=________
°
.
三、 解答题 (本题共计 9 小题 ,共计60分 , )
21.(6分) 如图,已知梯形????????中,?????//?????,∠??=
90
°
,????+????=????,以????为直径作⊙??.
/
(1)求证:????为⊙??的切线;
(2)试探索以????为直径的圆与????有怎样的位置关系?证明你的结论.
?
22.(6分) 一个边长为4????的等边三角形??????与⊙??等高,如图放置,⊙??与????相切于点??,⊙??与????相交于点??.
/
(1)求????的长;
(2)将⊙??在射线????上向左滚动,当⊙??与????相切时,则圆心??经过的距离是多少(直接写出结论).
?
23.(6分) 如图已知????是半径,弦????垂直????于??,点??是????上的一点,????和⊙??相交于另一点??,过点??的切线和????的延长线交于点??:
/
(1)求证:????=????;??
(2)当????:????=1:8,????=
2
时,求?????????的值.
?
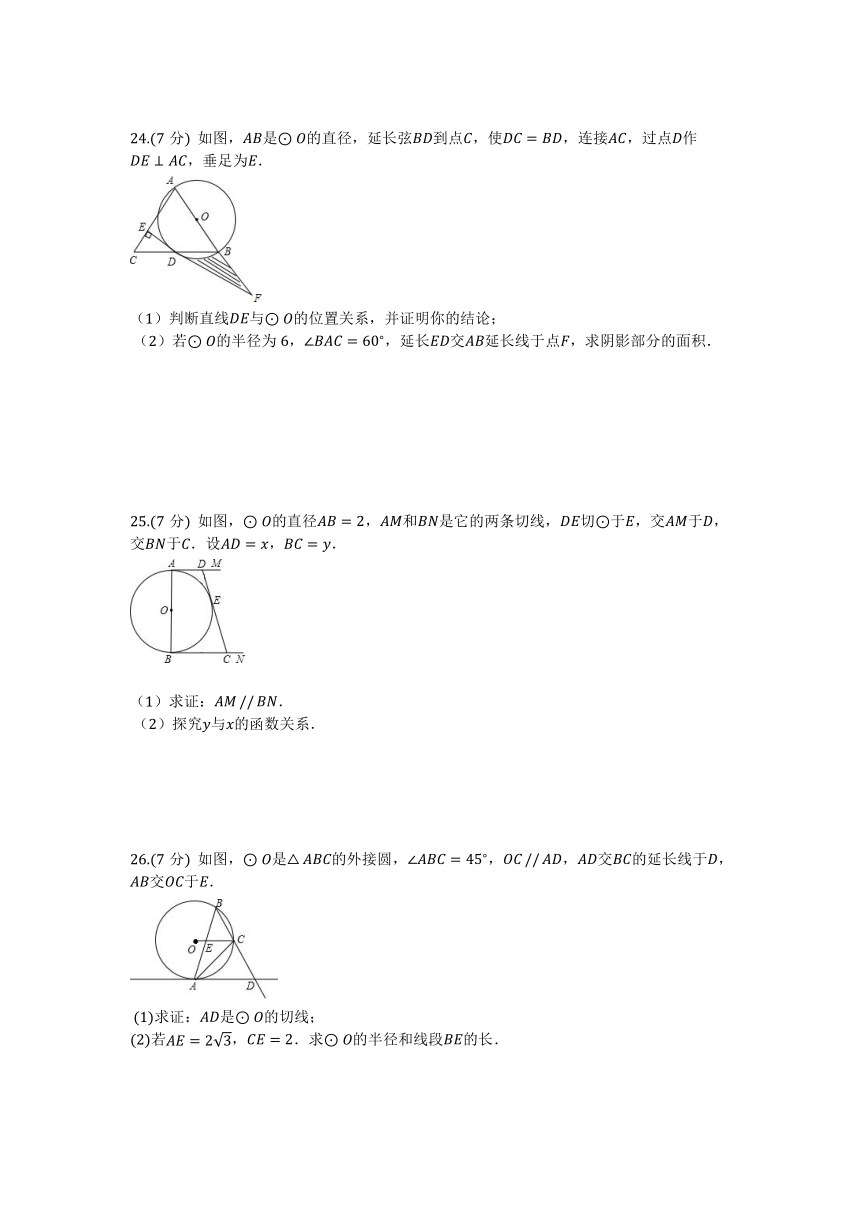
24.(7分) 如图,????是⊙??的直径,延长弦????到点??,使????=????,连接????,过点??作????⊥????,垂足为??.
/
(1)判断直线????与⊙??的位置关系,并证明你的结论;
(2)若⊙??的半径为6,∠??????=
60
°
,延长????交????延长线于点??,求阴影部分的面积.
?
25.(7分) 如图,⊙??的直径????=2,????和????是它的两条切线,????切⊙于??,交????于??,交????于??.设????=??,????=??.
/
(1)求证:?????//?????.
(2)探究??与??的函数关系.
?
26.(7分) 如图,⊙??是△??????的外接圆,∠??????=
45
°
,?????//?????,????交????的延长线于??,????交????于??.
/
(1)求证:????是⊙??的切线;
(2)若????=2
3
,????=2.求⊙??的半径和线段????的长.
?
27(7分) 如图,????是⊙??的直径,????切⊙??于??,????⊥????于??,????⊥????于??,交⊙??于??,连接????、????.
/
(1)求证:????是∠??????的平分线;
(2)若∠??????=
60
°
,则????与????是否平行?请说明理由.
?
28.(7分) 已知,如图,在????△??????中,∠??=
90
°
,以????为直径作⊙??,交????于??,过??作?????//?????交????于??.
/
(1)求证:????是⊙??的切线.
(2)如果⊙??的半径为
3
2
,????=2,求????的长.
答案
1. C
2. C
3. D
4. A
5. C
6. B
7. C
8. B
9. C
10. C
11. 10
12.
60
°
13. 6
14. 48
15. 6
16. 3或7
17. 5
18.
2
3
19. 4
20. 66
21. (1)证明:过点??作????⊥????于点??, ∵在梯形????????中,?????//?????,∠??=
90
°
, ∴????⊥????,????⊥????, ∴?????//??????//?????, ∵????=????, ∴????是梯形????????的中位线, ∴????=
1
2
(????+????), ∵????+????=????, ∴????=
1
2
????, ∵以????为直径作⊙??. ∴直线????是⊙??的切线.
/
(2)设圆心为??′.过点??′作??′??⊥????于点??,过点??′作??′???//?????, ∴??′??是梯形????????的中位线, ∴??′??=
1
2
(????+????)=
1
2
????=????, ∴∠??′????=∠????′??,
/
∵?????//???′??, ∴∠??????′=∠????′??=∠??′????, 在△????′??和△????′??中,
∠??????′=∠??????′
∠??=∠??′????=
90
°
??′??=??′??
, ∴△????′???△????′??(??????), ∴??′??=??′??=
1
2
????, 即????与⊙??′相切.
22. 解:(1)如图1,连接????,并过点??作????⊥????于??, ∵△??????为等边三角形,边长为4????, ∴△??????的高为2
3
????, ∴????=
3
????, 又∵∠??????=
60
°
, ∴∠??????=
30
°
, 在????△??????中,可得????=
3
2
????, 即????=2????=3????;
/
(2)
/
如图2,设⊙??与????相切于??,与????相切于??, ∴????的长度即为圆心??经过的距离, ∵∠??????=
90
°
,∠??=
30
°
, ∴????=
1
2
????, 在△??????与△??????中,
∠??=∠??=
60
°
∠??????=∠??????=
90
°
????=????
, ∴△???????△??????, ∴????=????=
1
2
????=2, ∴????=1????, ∴圆心??经过的距离是1????.
23. 解:(1)连接????,则有∠1=∠2, 又????是切线,∴????⊥????, 而∠4与∠1互余,∠3与∠2互余, ∴∠3=∠4, ∴????=????
/
(2)∵????=
2
, ∴????=8
2
, 又∵??
??
2
=?????????=
2
?9
2
=18, ∴????=3
2
=???? ∴????=3
2
?
2
=2
2
,????=6
2
∴?????????=?????????=24.
24. (1)
/
直线????与⊙??的位置关系是相切, 证明:连接????, ∵????=????,????=????, ∴?????//?????, ∵????⊥????, ∴????⊥????, ∵????为半径, 直线????是⊙??的切线, 即直线????与⊙??的位置关系是相切;(2)解:∵?????//?????,∠??????=
60
°
, ∴∠??????=∠??=
60
°
, ∵????是⊙??切线, ∴∠??????=
90
°
, ∴∠??=
30
°
, ∴????=2????=12, 由勾股定理得:????=6
3
, ∴阴影部分的面积??=
??
△??????
?
??
扇形??????
=
1
2
×6×6
3
?
60??×
6
2
360
=18
3
?6??.
25. (1)证明:∵????和????是⊙??的两条切线, ∴????⊥????,????⊥????, ∴?????//?????.
/
(2)解:作????⊥????交????于??, ∵????⊥????,????⊥????. 又∵????⊥????, ∴∠??????=∠??????=∠??????=
90
°
, ∴四边形????????是矩形, ∴????=????=??,????=????=2, ∵????=??, ∴????=?????????=?????; ∵????和????是⊙??的两条切线,????切⊙??于??, ∴????=????=??????=????=??, 则????=????+????=??+??, 在????△??????中, 由勾股定理得:(??+??
)
2
=(?????
)
2
+
2
2
, 整理为:??=
1
??
, ∴??与??的函数关系为:??=
1
??
.
26. (1)证明:连结????,如图, ∵∠??????=
45
,(同弧所对圆心角是圆周角的两倍) ∴∠??????=
90
; ∵????∥????, ∴∠??????=
90
,即????⊥????; ∴????是⊙O的切线.
/
(2)解:设⊙??的半径为??,则????=??,????=???2,????=2
3
, 在????△??????中,∵??
??
2
+??
??
2
=??
??
2
, ∴
??
2
+(???2
)
2
=(2
3
)
2
,解得??=1+
5
,(负值舍去), 如图:延长????交⊙??于??,连接????, 则△??????∽△??????, ∴
????
????
=
????
????
, ∵????=2???2=2
5
, ∴????=
2
15
3
.
/
27 (1)证明:连接????; ∵????是⊙??的直径, ∴∠??????=
90
°
. ∵????切圆于??, ∴∠??????=∠??????,又????⊥????. ∴∠??????=∠??????. 即????是∠??????的平分线.
/
(2)解:?????//?????.理由如下: ∵????⊥????于??,????⊥????于??, ∴?????//?????. ∴∠??????=
180
°
?∠??=
120
°
. ∵????是∠??????的平分线, ∴∠??????=
60
°
. ∴∠??????=∠??????=
60
°
(圆内接四边形的任意一个外角等于它的内对角), ∴∠??????=∠??????. ∴?????//?????.
28. (1)证明:连接????,如图所示:
/
∵?????//?????, ∴∠∠1=∠??,∠2=∠3, ∵????=????, ∴∠??=∠3, ∴∠1=∠2, 在△??????和△??????中,
????=????
??????;
∠1=∠2
??????;
????=????
??????;
, ∴△???????△??????(??????), ∴∠??????=∠??=
90
°
, ∴????⊥????, ∴????是⊙??的切线.(2)解:∵△???????△??????, ∴????=????=2, ∴????=
??
??
2
+??
??
2
=
(
3
2
)
2
+
2
2
=2.5, ∵????=????,?????//?????, ∴????是△??????的中位线, ∴????=2????=5.
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
1. 已知⊙??的直径????=6????,则圆上任意一点到圆心的距离等于( )
A.2?????
B.2.5?????
C.3?????
D.无法确定
?2. 已知????是⊙??的直径,????′⊥????,????、????分别与圆相交于??、??,那么下列等式中一定成立的是( )
/
A.?????????=?????????
B.?????????=?????????′
C.?????????=?????????
D.?????????=?????????
?3. 下列说法中正确的是( )
A.垂直于半径的直线是圆的切线 B.圆的切线垂直于半径
C.经过半径的外端的直线是圆的切线 D.圆的切线垂直于过切点的半径
?4. 到三角形三条边的距离相等的点是三角形( )的交点.
A.三个内角平分线
B.三边垂直平分线
C.三条中线
D.三条高线
?5. 如图,点??是⊙??直径????的延长线上一点,????切⊙??于点??,已知????=3,????=2.则????等于( )
/
A.2
B.3
C.4
D.5
?6. 如图,⊙??中弦????垂直于直径????于点??,则下列结论:①????=????;②
????
=
????
;③
????
=
????
;④????=????,其中正确的有( )
/
A.①②③④
B.①②③
C.②③④
D.①④
?7. 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面????宽为8????,水面最深地方的高度为2????,则该输水管的半径为( )
/
A.3????
B.4????
C.5????
D.6????
?8. 如图,已知????,????分别切⊙??于点??、??,∠??=
60
°
,????=8,那么弦????的长是( )
/
A.4
B.8
C.4
3
D.8
3
?9. 有一边长为2
3
的正三角形,则它的外接圆的面积为( )
A.2
3
??
B.4
3
??
C.4??
D.12??
?10. 如图,已知????是⊙??的直径,??是⊙??上的点,sin??=
1
4
,????=1,则⊙??的半径等于( )
/
A.4
B.3
C.2
D.
15
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 一个扇形的弧长是38??????,面积是190????
??
2
,这个扇形的半径是________????.
?12. 如图,已知四边形????????内接于⊙??,∠??????=
60
°
,则∠??????的度数是________.
////
第12题 第13题 第14题 第15题
?13. 如图,在⊙??中,弦????与????相交于点??,已知????=3????,????=4????,????=2????,那么????=________????.
?14. 如图????是⊙??的直径,∠??????=
42
°
,点??是弦????的中点,则∠??????的度数是________度.
?15. 如图,????是⊙??的直径,????是垂直于????的弦,垂足为??,已知????=10,????=9,则????=________.
?16. 平面上的一点和⊙??的最近点距离为4????,最远距离为10????,则这圆的半径是________????.
?17. 如图,在⊙O中,OB为半径,AB是⊙O的切线,OA与⊙O相交于点C,∠A=30°,OA=8,则阴影部分的面积是________. / / / /
第17题图 第18题 第19题 第20题
?18. 如图,⊙??是△??????的外接圆,????是⊙??的直径,若⊙??的半径为
3
2
,????=2,sin??的值是________.
19. 如图,摩天轮⊙??的最高处??到地面??的距离是82米,最低处??到地面??的距离是2米.若游客从??处乘摩天轮绕一周需12分钟,则游客从??处乘摩天轮到地面??的距离是62米时最少需________分钟.
?20. 如图,点??、??、??在⊙??上,若∠??????=
24
°
,则∠??????=________
°
.
三、 解答题 (本题共计 9 小题 ,共计60分 , )
21.(6分) 如图,已知梯形????????中,?????//?????,∠??=
90
°
,????+????=????,以????为直径作⊙??.
/
(1)求证:????为⊙??的切线;
(2)试探索以????为直径的圆与????有怎样的位置关系?证明你的结论.
?
22.(6分) 一个边长为4????的等边三角形??????与⊙??等高,如图放置,⊙??与????相切于点??,⊙??与????相交于点??.
/
(1)求????的长;
(2)将⊙??在射线????上向左滚动,当⊙??与????相切时,则圆心??经过的距离是多少(直接写出结论).
?
23.(6分) 如图已知????是半径,弦????垂直????于??,点??是????上的一点,????和⊙??相交于另一点??,过点??的切线和????的延长线交于点??:
/
(1)求证:????=????;??
(2)当????:????=1:8,????=
2
时,求?????????的值.
?
24.(7分) 如图,????是⊙??的直径,延长弦????到点??,使????=????,连接????,过点??作????⊥????,垂足为??.
/
(1)判断直线????与⊙??的位置关系,并证明你的结论;
(2)若⊙??的半径为6,∠??????=
60
°
,延长????交????延长线于点??,求阴影部分的面积.
?
25.(7分) 如图,⊙??的直径????=2,????和????是它的两条切线,????切⊙于??,交????于??,交????于??.设????=??,????=??.
/
(1)求证:?????//?????.
(2)探究??与??的函数关系.
?
26.(7分) 如图,⊙??是△??????的外接圆,∠??????=
45
°
,?????//?????,????交????的延长线于??,????交????于??.
/
(1)求证:????是⊙??的切线;
(2)若????=2
3
,????=2.求⊙??的半径和线段????的长.
?
27(7分) 如图,????是⊙??的直径,????切⊙??于??,????⊥????于??,????⊥????于??,交⊙??于??,连接????、????.
/
(1)求证:????是∠??????的平分线;
(2)若∠??????=
60
°
,则????与????是否平行?请说明理由.
?
28.(7分) 已知,如图,在????△??????中,∠??=
90
°
,以????为直径作⊙??,交????于??,过??作?????//?????交????于??.
/
(1)求证:????是⊙??的切线.
(2)如果⊙??的半径为
3
2
,????=2,求????的长.
答案
1. C
2. C
3. D
4. A
5. C
6. B
7. C
8. B
9. C
10. C
11. 10
12.
60
°
13. 6
14. 48
15. 6
16. 3或7
17. 5
18.
2
3
19. 4
20. 66
21. (1)证明:过点??作????⊥????于点??, ∵在梯形????????中,?????//?????,∠??=
90
°
, ∴????⊥????,????⊥????, ∴?????//??????//?????, ∵????=????, ∴????是梯形????????的中位线, ∴????=
1
2
(????+????), ∵????+????=????, ∴????=
1
2
????, ∵以????为直径作⊙??. ∴直线????是⊙??的切线.
/
(2)设圆心为??′.过点??′作??′??⊥????于点??,过点??′作??′???//?????, ∴??′??是梯形????????的中位线, ∴??′??=
1
2
(????+????)=
1
2
????=????, ∴∠??′????=∠????′??,
/
∵?????//???′??, ∴∠??????′=∠????′??=∠??′????, 在△????′??和△????′??中,
∠??????′=∠??????′
∠??=∠??′????=
90
°
??′??=??′??
, ∴△????′???△????′??(??????), ∴??′??=??′??=
1
2
????, 即????与⊙??′相切.
22. 解:(1)如图1,连接????,并过点??作????⊥????于??, ∵△??????为等边三角形,边长为4????, ∴△??????的高为2
3
????, ∴????=
3
????, 又∵∠??????=
60
°
, ∴∠??????=
30
°
, 在????△??????中,可得????=
3
2
????, 即????=2????=3????;
/
(2)
/
如图2,设⊙??与????相切于??,与????相切于??, ∴????的长度即为圆心??经过的距离, ∵∠??????=
90
°
,∠??=
30
°
, ∴????=
1
2
????, 在△??????与△??????中,
∠??=∠??=
60
°
∠??????=∠??????=
90
°
????=????
, ∴△???????△??????, ∴????=????=
1
2
????=2, ∴????=1????, ∴圆心??经过的距离是1????.
23. 解:(1)连接????,则有∠1=∠2, 又????是切线,∴????⊥????, 而∠4与∠1互余,∠3与∠2互余, ∴∠3=∠4, ∴????=????
/
(2)∵????=
2
, ∴????=8
2
, 又∵??
??
2
=?????????=
2
?9
2
=18, ∴????=3
2
=???? ∴????=3
2
?
2
=2
2
,????=6
2
∴?????????=?????????=24.
24. (1)
/
直线????与⊙??的位置关系是相切, 证明:连接????, ∵????=????,????=????, ∴?????//?????, ∵????⊥????, ∴????⊥????, ∵????为半径, 直线????是⊙??的切线, 即直线????与⊙??的位置关系是相切;(2)解:∵?????//?????,∠??????=
60
°
, ∴∠??????=∠??=
60
°
, ∵????是⊙??切线, ∴∠??????=
90
°
, ∴∠??=
30
°
, ∴????=2????=12, 由勾股定理得:????=6
3
, ∴阴影部分的面积??=
??
△??????
?
??
扇形??????
=
1
2
×6×6
3
?
60??×
6
2
360
=18
3
?6??.
25. (1)证明:∵????和????是⊙??的两条切线, ∴????⊥????,????⊥????, ∴?????//?????.
/
(2)解:作????⊥????交????于??, ∵????⊥????,????⊥????. 又∵????⊥????, ∴∠??????=∠??????=∠??????=
90
°
, ∴四边形????????是矩形, ∴????=????=??,????=????=2, ∵????=??, ∴????=?????????=?????; ∵????和????是⊙??的两条切线,????切⊙??于??, ∴????=????=??????=????=??, 则????=????+????=??+??, 在????△??????中, 由勾股定理得:(??+??
)
2
=(?????
)
2
+
2
2
, 整理为:??=
1
??
, ∴??与??的函数关系为:??=
1
??
.
26. (1)证明:连结????,如图, ∵∠??????=
45
,(同弧所对圆心角是圆周角的两倍) ∴∠??????=
90
; ∵????∥????, ∴∠??????=
90
,即????⊥????; ∴????是⊙O的切线.
/
(2)解:设⊙??的半径为??,则????=??,????=???2,????=2
3
, 在????△??????中,∵??
??
2
+??
??
2
=??
??
2
, ∴
??
2
+(???2
)
2
=(2
3
)
2
,解得??=1+
5
,(负值舍去), 如图:延长????交⊙??于??,连接????, 则△??????∽△??????, ∴
????
????
=
????
????
, ∵????=2???2=2
5
, ∴????=
2
15
3
.
/
27 (1)证明:连接????; ∵????是⊙??的直径, ∴∠??????=
90
°
. ∵????切圆于??, ∴∠??????=∠??????,又????⊥????. ∴∠??????=∠??????. 即????是∠??????的平分线.
/
(2)解:?????//?????.理由如下: ∵????⊥????于??,????⊥????于??, ∴?????//?????. ∴∠??????=
180
°
?∠??=
120
°
. ∵????是∠??????的平分线, ∴∠??????=
60
°
. ∴∠??????=∠??????=
60
°
(圆内接四边形的任意一个外角等于它的内对角), ∴∠??????=∠??????. ∴?????//?????.
28. (1)证明:连接????,如图所示:
/
∵?????//?????, ∴∠∠1=∠??,∠2=∠3, ∵????=????, ∴∠??=∠3, ∴∠1=∠2, 在△??????和△??????中,
????=????
??????;
∠1=∠2
??????;
????=????
??????;
, ∴△???????△??????(??????), ∴∠??????=∠??=
90
°
, ∴????⊥????, ∴????是⊙??的切线.(2)解:∵△???????△??????, ∴????=????=2, ∴????=
??
??
2
+??
??
2
=
(
3
2
)
2
+
2
2
=2.5, ∵????=????,?????//?????, ∴????是△??????的中位线, ∴????=2????=5.
