2018年高中数学人教A版必修3 第一章 算法初步 单元测试题(解析版)
文档属性
| 名称 | 2018年高中数学人教A版必修3 第一章 算法初步 单元测试题(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-20 09:28:22 | ||
图片预览




文档简介
2018年高中数学人教A版必修3 第一章 算法初步 单元测试题
一.选择题(共12小题)
1.函数f(x)=x+lnx﹣3的零点位于区间( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
2.在下列区间中,函数f(x)=ex+4x﹣3的零点所在的区间为( )
A. B. C. D.
3.设f(x)=lgx+x﹣3,用二分法求方程lgx+x﹣3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间( )
A.(2,2.25) B.(2.25,2.5) C.(2.5,2.75) D.(2.75,3)
4.定义在R上的奇函数f(x)=a?2x﹣2﹣x﹣4sinx的一个零点所在区间为( )
A.(﹣a,0) B.(0,a) C.(a,3) D.(3,a+3)
5.用二分法求函数f(x)=x3+5的零点可以取的初始区间是( )
A.[﹣2,1] B.[﹣1,0] C.[0,1] D.[1,2]
6.函数f(x)=lnx+3x﹣7的零点所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
7.算法框图中表示判断的是( )
A. B. C. D.
8.用秦九韶算法求多项式f(x)=1+2x+x2﹣3x3+2x4在x=﹣1时的值,v2的结果是( )
A.﹣4 B.﹣1 C.5 D.6
9.以下是解决数学问题的思维过程的流程图:
在此流程图中,①②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
A.①﹣综合法,②﹣分析法 B.①﹣分析法,②﹣综合法
C.①﹣综合法,②﹣反证法 D.①﹣分析法,②﹣反证法
10.如图执行的程序的功能是( )
A.求两个正整数的最大公约数
B.求两个正整数的最大值
C.求两个正整数的最小值
D.求圆周率的不足近似值
11.如程序框图所示,其作用是输入x的值,输出相应的y的值.若要使输入的x的值与输出的y的值相等,则这样的x的值有( )
A.1个 B.2个 C.3个 D.4个
12.运行如图的程序框图,设输出数据构成的集合为A,从集合A中任取一个元素a,则函数y=xa,x∈[0,+∞)是增函数的概率为( )
A. B. C. D.
二.填空题(共4小题)
13.用二分法求方程x3﹣2x﹣5=0在区间(2,4)上的实数根时,取中点x1=3,则下一个有根区间是 .
14.函数的一个零点在区间(1,2)内,则实数a的取值范围是 .
15.顾客请一位工艺师把A,B两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件原料先由徒弟完成粗加工,再由师傅进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:
工序时间原料 粗加工 精加工
原料A 9 15
原料B 6 21
则最短交货期为 个工作日.
16.把二进制数1011(2)化成十进制数为 .
三.解答题(共6小题)
17.用秦九韶算法求多项式f(x)=8x7+5x6+3x4+2x+1,当x=2时的值.
18.已知一个5次多项式为f(x)=4x5﹣3x3+2x2+5x+1,用秦九韶算法求这个多项式当x=2时的值.
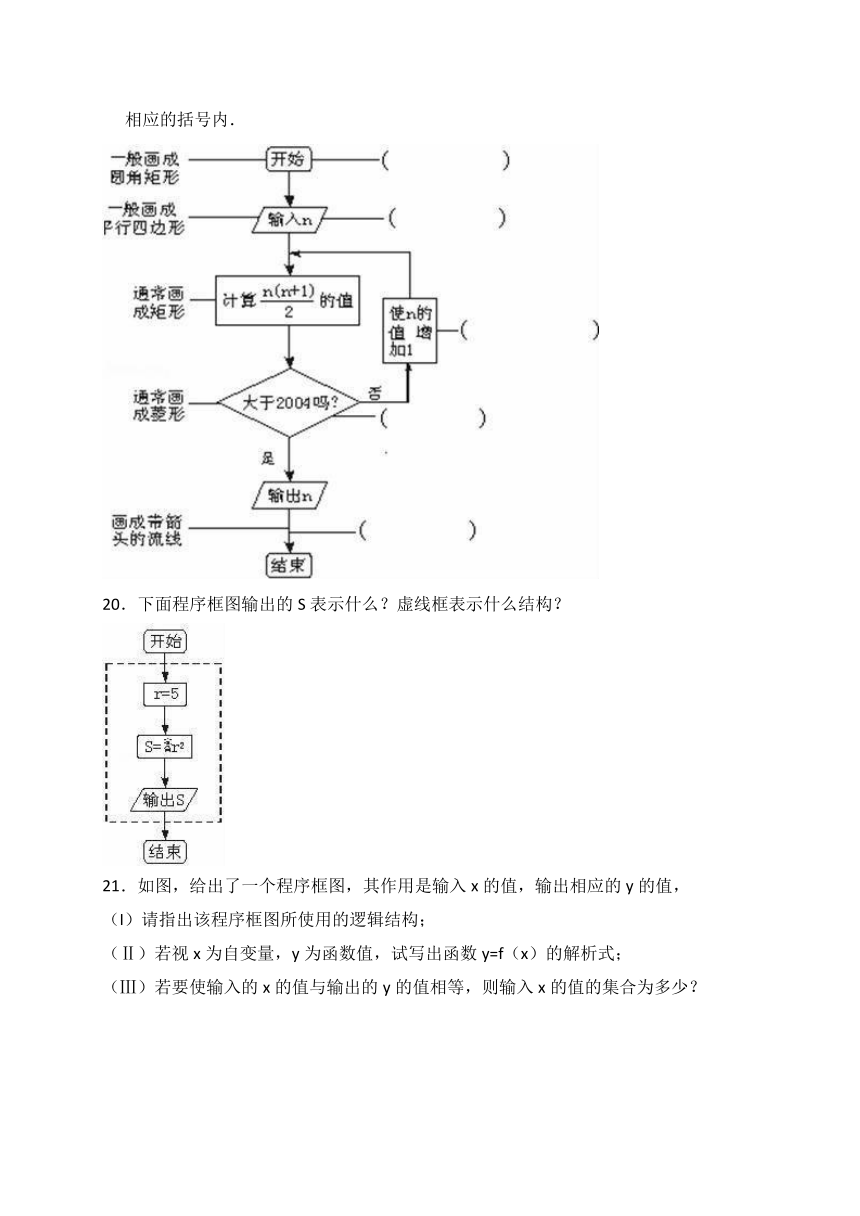
19.请从下面具体的例子中说明几个基本的程序框和它们各自表示的功能,并把它填在相应的括号内.
20.下面程序框图输出的S表示什么?虚线框表示什么结构?
21.如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视x为自变量,y为函数值,试写出函数y=f(x)的解析式;
(Ⅲ)若要使输入的x的值与输出的y的值相等,则输入x的值的集合为多少?
22.如图是计算1+2++3++…+2010+的值的程序框图,
(1)图中空白的判断框应填 ?处理框应填 ;
(2)写出与程序框图相对应的程序.
2018年高中数学人教A版必修3 第一章 算法初步 单元测试题
参考答案与试题解析
一.选择题(共12小题)
1.函数f(x)=x+lnx﹣3的零点位于区间( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
【分析】对f(x)进行求导,得到其单调性,再利用零点定理进行判断;
【解答】解:函数f(x)=x+lnx﹣3,(x>0)
∴f′(x)=1+,可得f′(x)>0,f(x)为增函数,
f(1)=1+0﹣3=﹣2<0,
f(2)=2+ln2﹣3=ln2﹣1<0,
f(3)=3+ln3﹣3=ln3>0,
∵f(2)f(3)<0,
所以f(x)的零点所在区间为(2,3),
故选:C.
【点评】此题主要考查函数零点的判定定理,此题主要函数的定义域x>0,此题是一道基础题;
2.在下列区间中,函数f(x)=ex+4x﹣3的零点所在的区间为( )
A. B. C. D.
【分析】根据导函数判断函数f(x)=ex+4x﹣3单调递增,运用零点判定定理,判定区间.
【解答】解:∵函数f(x)=ex+4x﹣3,
∴f′(x)=ex+4>0,
∴函数f(x)=ex+4x﹣3在(﹣∞,+∞)上为增函数,
∵f()=+1﹣3<0,
f()=+2﹣3=﹣1>0,
∴f()?f()<0,
∴函数f(x)=ex+4x﹣3的零点所在的区间为(,)
故选:C.
【点评】本题考察了函数零点的判断方法,借助导数,函数值,属于中档题.
3.设f(x)=lgx+x﹣3,用二分法求方程lgx+x﹣3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间( )
A.(2,2.25) B.(2.25,2.5) C.(2.5,2.75) D.(2.75,3)
【分析】由已知“方程lgx+x﹣3=0在x∈(2,3)内近似解”,且具体的函数值的符号也已确定,由f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,即可求得结果.
【解答】解析:∵f(2.5)?f(2.75)<0,
由零点存在定理,得,
∴方程的根落在区间(2.5,2.75).
故选:C.
【点评】二分法是求方程根的一种算法,其理论依据是零点存在定理:
一般地,若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,
且f(a)f(b)<0,则函数y=f(x)在区间(a,b)上有零点.
4.定义在R上的奇函数f(x)=a?2x﹣2﹣x﹣4sinx的一个零点所在区间为( )
A.(﹣a,0) B.(0,a) C.(a,3) D.(3,a+3)
【分析】根据奇函数的性质求出a的值,再很据f(1)?f(3)<0,即可求出答案.
【解答】解:∵定义在R上的奇函数f(x)=a?2x﹣2﹣x﹣4sinx,
∴f(0)=a﹣1=0,
解得a=1,
∴f(x)=2x﹣2﹣x﹣4sinx,
∴f(1)=1﹣2﹣4sin1<0,f(3)=8﹣﹣4sin3>0,
∴f(1)?f(3)<0,
∴函数一个零点所在的区间为(a,3),、
故选:C.
【点评】本题考查了奇函数的性质和函数的零点存在定理,属于基础题.
5.用二分法求函数f(x)=x3+5的零点可以取的初始区间是( )
A.[﹣2,1] B.[﹣1,0] C.[0,1] D.[1,2]
【分析】由于函数只有满足在零点两侧的函数值异号时,才可用二分法求函数f(x)的零点,经检验,A满足条件.
【解答】解:二分法求变号零点时所取初始区间[a,b],应满足使f(a)?f(b)<0.
由于本题中函数f(x)=x3+5,由于f(﹣2)=﹣3,f(1)=6,显然满足f(﹣2)?f(1)<0,
故函数f(x)=x3+5的零点可以取的初始区间是[﹣2,1],
故选:A.
【点评】本题主要考查函数的零点的定义,注意函数只有满足在零点两侧的函数值异号时,才可用二分法求函数f(x)的零点,属于基础题.
6.函数f(x)=lnx+3x﹣7的零点所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
【分析】由函数的解析式求得f(2)f(3)<0,再根据根据函数零点的判定定理可得函数f(x)的零点所在的区间.
【解答】解:∵函数f(x)=lnx+3x﹣7在其定义域上单调递增,
∴f(2)=ln2+2×3﹣7=ln2﹣1<0,f(3)=ln3+9﹣7=ln3+2>0,
∴f(2)f(3)<0.
根据函数零点的判定定理可得函数f(x)的零点所在的区间是(2,3),
故选:C.
【点评】本题主要考查求函数的值,函数零点的判定定理,属于基础题.
7.算法框图中表示判断的是( )
A. B. C. D.
【分析】根据算法框图中表示判断的是菱形框,故选择菱形框,得到结果.
【解答】解:∵在算法框图中,表示判断的是菱形,
故选:B.
【点评】本题考查算法的特点,本题解题的关键是知道几种不同的几何图形所表示的意义,才能正确选择.
8.用秦九韶算法求多项式f(x)=1+2x+x2﹣3x3+2x4在x=﹣1时的值,v2的结果是( )
A.﹣4 B.﹣1 C.5 D.6
【分析】本题考查秦九韶算法,考查在用秦九韶算法解题时进行的加法和乘法运算,是一个基础题,先计算v1=anx+an﹣1;再计算v2=v1x+an﹣2,即得.
【解答】解:v1=2×(﹣1)﹣3=﹣5;
∴v2=(﹣5)×(﹣1)+1=6,
故选:D.
【点评】秦九韶算法的设计思想:一般地对于一个n次多项式f(x)=anxn+an﹣1xn﹣1+an﹣2xn﹣2+…+a1x+a0,首先改写成如下形式:f(x)=(…(anx+an﹣1)x+an﹣2)x+…+a1)x+a0,再计算最内层括号内一次多项式的值,即v1=anx+an﹣1;然后由内向外逐层计算一多项式的值,即v2=v1x+an﹣2,v3=v2x+an﹣3,…,vn=vn﹣1x+a0.
9.以下是解决数学问题的思维过程的流程图:
在此流程图中,①②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
A.①﹣综合法,②﹣分析法 B.①﹣分析法,②﹣综合法
C.①﹣综合法,②﹣反证法 D.①﹣分析法,②﹣反证法
【分析】根据综合法和分析法的定义,可知由已知到可知进而得到结论的应为综合法,由未知到需知,进而找到与已知的关系为分析法,进而得到答案.
【解答】解:根据已知可得该结构图为证明方法的结构图:
∵由已知到可知,进而得到结论的应为综合法,
由未知到需知,进而找到与已知的关系为分析法,
故①②两条流程线与“推理与证明”中的思维方法为:
①﹣综合法,②﹣分析法,
故选:A.
【点评】本题以结构图为载体,考查了证明方法的定义,正确理解综合法和分析法的定义,是解答的关键.
10.如图执行的程序的功能是( )
A.求两个正整数的最大公约数
B.求两个正整数的最大值
C.求两个正整数的最小值
D.求圆周率的不足近似值
【分析】由算法程序可知,用辗转相除法求m,n两数的最大公约数,由此可得答案.
【解答】解:由算法程序可知,用辗转相除法求m,n两数的最大公约数,
输出的数为m、n的最大公约数.
故选:A.
【点评】本题考查了直到型循环结构的程序框图,考查了算法案例辗转相除法求m,n两数的最大公约数,读懂程序语言是关键.
11.如程序框图所示,其作用是输入x的值,输出相应的y的值.若要使输入的x的值与输出的y的值相等,则这样的x的值有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是求分段函数的函数值.
【解答】解:这是一个用条件分支结构设计的算法,
该程序框图所表示的算法的作用是求分段函数y=的函数值,
当x≤2时,令x2=x,得x=0或1;
当2<x≤5时,令2x﹣3=x,得x=3;
当x>5时,令=x,得x=±1(舍去),
故只有3个值符合题意.
故选:C.
【点评】根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)?②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.
12.运行如图的程序框图,设输出数据构成的集合为A,从集合A中任取一个元素a,则函数y=xa,x∈[0,+∞)是增函数的概率为( )
A. B. C. D.
【分析】先根据流程图进行逐一进行运行,求出集合A,再求出基本事件的总数,然后讨论满足“函数y=xα,x∈[0,+∞)是增函数”时包含基本事件,最后根据古典概型公式求出该概率即可.
【解答】解:由框图可知A={3,0,﹣1,8,15},
其中基本事件的总数为5,
设集合中满足“函数y=xα,x∈[0,+∞)是增函数”为事件E,
当函数y=xα,x∈[0,+∞)是增函数时,α>0
事件E包含基本事件为3,
则.
故选:C.
【点评】本题主要考查了当型循环结构,以及与集合和古典概型相结合等问题,算法与其他知识结合在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.
二.填空题(共4小题)
13.用二分法求方程x3﹣2x﹣5=0在区间(2,4)上的实数根时,取中点x1=3,则下一个有根区间是 (2,3) .
【分析】构造函数f(x)=x3﹣2x﹣5,确定f(2),f(3),f(4)的符号,根据零点存在定理,即可得到结论.
【解答】解:设函数f(x)=x3﹣2x﹣5,则
∵f(2)=﹣1<0,f(3)=16>0,f(4)=51>0
∴下一个有根区间是(2,3).
故答案为:(2,3).
【点评】本题考查二分法,考查零点存在定理,考查学生的计算能力,属于基础题.
14.函数的一个零点在区间(1,2)内,则实数a的取值范围是 (0,3) .
【分析】由题意可得f(1)f(2)=(0﹣a)(3﹣a)<0,解不等式求得实数a的取值范围.
【解答】解:由题意可得f(1)f(2)=(0﹣a)(3﹣a)<0,
解得:0<a<3,
故实数a的取值范围是(0,3),
故答案为:(0,3)
【点评】本题考查函数零点的定义以及函数零点判定定理的应用,属于基础题.
15.顾客请一位工艺师把A,B两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件原料先由徒弟完成粗加工,再由师傅进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:
工序时间原料 粗加工 精加工
原料A 9 15
原料B 6 21
则最短交货期为 42 个工作日.
【分析】先完成B的加工,再完成A的加工即可.
【解答】解:由题意,徒弟利用6天完成原料B的加工,由师傅利用21天完成精加工,与此同时,徒弟利用9天完成原料A的加工,最后由师傅利用15天完成精加工,故最短交货期为6+21+15=42 个工作日.
故答案为:42.
【点评】本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,属于基础题.
16.把二进制数1011(2)化成十进制数为 11 .
【分析】欲将二进制数1011用十进制表示,只须根据转换公式:1×23+0×22+1×21+1进行计算即得.
【解答】解:二进制数1011用十进制可以表示为:
1×23+0×22+1×21+1=11.
故答案为:11.
【点评】本题主要考查了算法的概念以及二进制数与用十进制的互化,属于基础题.
三.解答题(共6小题)
17.用秦九韶算法求多项式f(x)=8x7+5x6+3x4+2x+1,当x=2时的值.
【分析】利用秦九韶算法一步一步地代入运算,注意本题中有几项不存在,此时在计算时,我们应该将这些项加上,比如含有x3这一项可看作0?x3.
【解答】解:根据秦九韶算法,把多项式改写成如下形式
f(x)=8x7+5x6+0?x5+3?x4+0?x3+0?x2+2x+1
=((((((8x+5)x+0)x+3)x+0)x+0)x+2)x+1
v0=8,v1=8×2+5=21
v2=21×2+0=42,v3=42×2+3=87
v4=87×2+0=174,v5=174×2+0=348
v6=348×2+2=698,v7=698×2+1=1397.
∴当x=2时,多项式的值为1397.
【点评】一般地,一元n次多项式的求值需要经过次乘法和n次加法,而秦九韶算法只需要n次乘法和n次加法.
18.已知一个5次多项式为f(x)=4x5﹣3x3+2x2+5x+1,用秦九韶算法求这个多项式当x=2时的值.
【分析】把所给的多项式写成关于x的一次函数的形式,依次写出,得到最后结果,从里到外进行运算,得到要求的值.
【解答】解:由f(x)=((((4x+0)x﹣3)x+2)x+5)x+1
∴v0=4
v1=4×2+0=8
v2=8×2﹣3=13
v3=13×2+2=28
v4=28×2+5=61
v5=61×2+1=123
故这个多项式当x=2时的值为123.
【点评】本题考查排序问题与算法的多样性,解答本题,关键是了解秦九韶算法的规则,求出多项式当x=2时的值.
19.请从下面具体的例子中说明几个基本的程序框和它们各自表示的功能,并把它填在相应的括号内.
【分析】在程序框图中,一个或几个程序框的组合表示算法中的一个步骤,带有方向箭头的流程线将程序框连接起来,表示算法的步骤的执行顺序,包括三个基本的逻辑结构.
【解答】解:
【点评】本题考查程序框图的概念,考查程序框图的三种逻辑结构,是一个基础题,从本题的知识点可以掌握本章的知识.
20.下面程序框图输出的S表示什么?虚线框表示什么结构?
【分析】由于圆的面积公式就是πr2,所以判断出输出的S是半径为5的圆面积.由框图三种结构的特点,此框图无判断框,是顺序结构.
【解答】解:由框图知,当r=5时,输出的s=πr2
所以程序框图输出的S表示:求半径为5的圆的面积的算法的程序框图,
虚线框是一个顺序结构.
【点评】本题考查圆的面积公式、考查程序框图中三种结构的特点,并由特点判断出是何种结构.
21.如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视x为自变量,y为函数值,试写出函数y=f(x)的解析式;
(Ⅲ)若要使输入的x的值与输出的y的值相等,则输入x的值的集合为多少?
【分析】(I)根据程序框图,可知该程序框图所使用的逻辑结构;
(Ⅱ)利用程序框图,可得分段函数的解析式;
(Ⅲ)利用分段函数,根据使输入的x的值与输出的y的值相等,建立方程,即可求得结论.
【解答】解:(I)程序框图所使用的逻辑结构是条件结构和顺序结构;…(2分)
(Ⅱ)解析式为:f(x)=…(7分)
(Ⅲ)依题意得,或,或,解得x=0,或x=1,或x=3
故所求的集合为{0,1,3}.…(13分)
【点评】本题考查程序框图,考查学生的读图能力,考查学生的计算能力,属于基础题.
22.如图是计算1+2++3++…+2010+的值的程序框图,
(1)图中空白的判断框应填 i≤2010 ?处理框应填 S=S+i+1/i ;
(2)写出与程序框图相对应的程序.
【分析】(1)本题考查的知识点是程序框图,由已知得本程序的作用是计算1+2++3++…+2010+,由于第一次执行循环时的循环变量初值为2,步长为1,最后一次执行循环进循环变量值为2010,我们根据利用循环结构进行累加的方法,不难给出结论.
(2)先判定循环的结构,然后选择对应的循环语句,对照流程图进行逐句写成语句即可.
【解答】解:(1)判断框:i≤2010
或i<2011;…(3分)
执行框:S=S+i+1/i…(6分)
(2)程序:如图…(12分)(全对才给分)
故答案为:i≤2010;S=S+i+1/i.
【点评】算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.
一.选择题(共12小题)
1.函数f(x)=x+lnx﹣3的零点位于区间( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
2.在下列区间中,函数f(x)=ex+4x﹣3的零点所在的区间为( )
A. B. C. D.
3.设f(x)=lgx+x﹣3,用二分法求方程lgx+x﹣3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间( )
A.(2,2.25) B.(2.25,2.5) C.(2.5,2.75) D.(2.75,3)
4.定义在R上的奇函数f(x)=a?2x﹣2﹣x﹣4sinx的一个零点所在区间为( )
A.(﹣a,0) B.(0,a) C.(a,3) D.(3,a+3)
5.用二分法求函数f(x)=x3+5的零点可以取的初始区间是( )
A.[﹣2,1] B.[﹣1,0] C.[0,1] D.[1,2]
6.函数f(x)=lnx+3x﹣7的零点所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
7.算法框图中表示判断的是( )
A. B. C. D.
8.用秦九韶算法求多项式f(x)=1+2x+x2﹣3x3+2x4在x=﹣1时的值,v2的结果是( )
A.﹣4 B.﹣1 C.5 D.6
9.以下是解决数学问题的思维过程的流程图:
在此流程图中,①②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
A.①﹣综合法,②﹣分析法 B.①﹣分析法,②﹣综合法
C.①﹣综合法,②﹣反证法 D.①﹣分析法,②﹣反证法
10.如图执行的程序的功能是( )
A.求两个正整数的最大公约数
B.求两个正整数的最大值
C.求两个正整数的最小值
D.求圆周率的不足近似值
11.如程序框图所示,其作用是输入x的值,输出相应的y的值.若要使输入的x的值与输出的y的值相等,则这样的x的值有( )
A.1个 B.2个 C.3个 D.4个
12.运行如图的程序框图,设输出数据构成的集合为A,从集合A中任取一个元素a,则函数y=xa,x∈[0,+∞)是增函数的概率为( )
A. B. C. D.
二.填空题(共4小题)
13.用二分法求方程x3﹣2x﹣5=0在区间(2,4)上的实数根时,取中点x1=3,则下一个有根区间是 .
14.函数的一个零点在区间(1,2)内,则实数a的取值范围是 .
15.顾客请一位工艺师把A,B两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件原料先由徒弟完成粗加工,再由师傅进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:
工序时间原料 粗加工 精加工
原料A 9 15
原料B 6 21
则最短交货期为 个工作日.
16.把二进制数1011(2)化成十进制数为 .
三.解答题(共6小题)
17.用秦九韶算法求多项式f(x)=8x7+5x6+3x4+2x+1,当x=2时的值.
18.已知一个5次多项式为f(x)=4x5﹣3x3+2x2+5x+1,用秦九韶算法求这个多项式当x=2时的值.
19.请从下面具体的例子中说明几个基本的程序框和它们各自表示的功能,并把它填在相应的括号内.
20.下面程序框图输出的S表示什么?虚线框表示什么结构?
21.如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视x为自变量,y为函数值,试写出函数y=f(x)的解析式;
(Ⅲ)若要使输入的x的值与输出的y的值相等,则输入x的值的集合为多少?
22.如图是计算1+2++3++…+2010+的值的程序框图,
(1)图中空白的判断框应填 ?处理框应填 ;
(2)写出与程序框图相对应的程序.
2018年高中数学人教A版必修3 第一章 算法初步 单元测试题
参考答案与试题解析
一.选择题(共12小题)
1.函数f(x)=x+lnx﹣3的零点位于区间( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
【分析】对f(x)进行求导,得到其单调性,再利用零点定理进行判断;
【解答】解:函数f(x)=x+lnx﹣3,(x>0)
∴f′(x)=1+,可得f′(x)>0,f(x)为增函数,
f(1)=1+0﹣3=﹣2<0,
f(2)=2+ln2﹣3=ln2﹣1<0,
f(3)=3+ln3﹣3=ln3>0,
∵f(2)f(3)<0,
所以f(x)的零点所在区间为(2,3),
故选:C.
【点评】此题主要考查函数零点的判定定理,此题主要函数的定义域x>0,此题是一道基础题;
2.在下列区间中,函数f(x)=ex+4x﹣3的零点所在的区间为( )
A. B. C. D.
【分析】根据导函数判断函数f(x)=ex+4x﹣3单调递增,运用零点判定定理,判定区间.
【解答】解:∵函数f(x)=ex+4x﹣3,
∴f′(x)=ex+4>0,
∴函数f(x)=ex+4x﹣3在(﹣∞,+∞)上为增函数,
∵f()=+1﹣3<0,
f()=+2﹣3=﹣1>0,
∴f()?f()<0,
∴函数f(x)=ex+4x﹣3的零点所在的区间为(,)
故选:C.
【点评】本题考察了函数零点的判断方法,借助导数,函数值,属于中档题.
3.设f(x)=lgx+x﹣3,用二分法求方程lgx+x﹣3=0在(2,3)内近似解的过程中得f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,则方程的根落在区间( )
A.(2,2.25) B.(2.25,2.5) C.(2.5,2.75) D.(2.75,3)
【分析】由已知“方程lgx+x﹣3=0在x∈(2,3)内近似解”,且具体的函数值的符号也已确定,由f(2.25)<0,f(2.75)>0,f(2.5)<0,f(3)>0,即可求得结果.
【解答】解析:∵f(2.5)?f(2.75)<0,
由零点存在定理,得,
∴方程的根落在区间(2.5,2.75).
故选:C.
【点评】二分法是求方程根的一种算法,其理论依据是零点存在定理:
一般地,若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,
且f(a)f(b)<0,则函数y=f(x)在区间(a,b)上有零点.
4.定义在R上的奇函数f(x)=a?2x﹣2﹣x﹣4sinx的一个零点所在区间为( )
A.(﹣a,0) B.(0,a) C.(a,3) D.(3,a+3)
【分析】根据奇函数的性质求出a的值,再很据f(1)?f(3)<0,即可求出答案.
【解答】解:∵定义在R上的奇函数f(x)=a?2x﹣2﹣x﹣4sinx,
∴f(0)=a﹣1=0,
解得a=1,
∴f(x)=2x﹣2﹣x﹣4sinx,
∴f(1)=1﹣2﹣4sin1<0,f(3)=8﹣﹣4sin3>0,
∴f(1)?f(3)<0,
∴函数一个零点所在的区间为(a,3),、
故选:C.
【点评】本题考查了奇函数的性质和函数的零点存在定理,属于基础题.
5.用二分法求函数f(x)=x3+5的零点可以取的初始区间是( )
A.[﹣2,1] B.[﹣1,0] C.[0,1] D.[1,2]
【分析】由于函数只有满足在零点两侧的函数值异号时,才可用二分法求函数f(x)的零点,经检验,A满足条件.
【解答】解:二分法求变号零点时所取初始区间[a,b],应满足使f(a)?f(b)<0.
由于本题中函数f(x)=x3+5,由于f(﹣2)=﹣3,f(1)=6,显然满足f(﹣2)?f(1)<0,
故函数f(x)=x3+5的零点可以取的初始区间是[﹣2,1],
故选:A.
【点评】本题主要考查函数的零点的定义,注意函数只有满足在零点两侧的函数值异号时,才可用二分法求函数f(x)的零点,属于基础题.
6.函数f(x)=lnx+3x﹣7的零点所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
【分析】由函数的解析式求得f(2)f(3)<0,再根据根据函数零点的判定定理可得函数f(x)的零点所在的区间.
【解答】解:∵函数f(x)=lnx+3x﹣7在其定义域上单调递增,
∴f(2)=ln2+2×3﹣7=ln2﹣1<0,f(3)=ln3+9﹣7=ln3+2>0,
∴f(2)f(3)<0.
根据函数零点的判定定理可得函数f(x)的零点所在的区间是(2,3),
故选:C.
【点评】本题主要考查求函数的值,函数零点的判定定理,属于基础题.
7.算法框图中表示判断的是( )
A. B. C. D.
【分析】根据算法框图中表示判断的是菱形框,故选择菱形框,得到结果.
【解答】解:∵在算法框图中,表示判断的是菱形,
故选:B.
【点评】本题考查算法的特点,本题解题的关键是知道几种不同的几何图形所表示的意义,才能正确选择.
8.用秦九韶算法求多项式f(x)=1+2x+x2﹣3x3+2x4在x=﹣1时的值,v2的结果是( )
A.﹣4 B.﹣1 C.5 D.6
【分析】本题考查秦九韶算法,考查在用秦九韶算法解题时进行的加法和乘法运算,是一个基础题,先计算v1=anx+an﹣1;再计算v2=v1x+an﹣2,即得.
【解答】解:v1=2×(﹣1)﹣3=﹣5;
∴v2=(﹣5)×(﹣1)+1=6,
故选:D.
【点评】秦九韶算法的设计思想:一般地对于一个n次多项式f(x)=anxn+an﹣1xn﹣1+an﹣2xn﹣2+…+a1x+a0,首先改写成如下形式:f(x)=(…(anx+an﹣1)x+an﹣2)x+…+a1)x+a0,再计算最内层括号内一次多项式的值,即v1=anx+an﹣1;然后由内向外逐层计算一多项式的值,即v2=v1x+an﹣2,v3=v2x+an﹣3,…,vn=vn﹣1x+a0.
9.以下是解决数学问题的思维过程的流程图:
在此流程图中,①②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
A.①﹣综合法,②﹣分析法 B.①﹣分析法,②﹣综合法
C.①﹣综合法,②﹣反证法 D.①﹣分析法,②﹣反证法
【分析】根据综合法和分析法的定义,可知由已知到可知进而得到结论的应为综合法,由未知到需知,进而找到与已知的关系为分析法,进而得到答案.
【解答】解:根据已知可得该结构图为证明方法的结构图:
∵由已知到可知,进而得到结论的应为综合法,
由未知到需知,进而找到与已知的关系为分析法,
故①②两条流程线与“推理与证明”中的思维方法为:
①﹣综合法,②﹣分析法,
故选:A.
【点评】本题以结构图为载体,考查了证明方法的定义,正确理解综合法和分析法的定义,是解答的关键.
10.如图执行的程序的功能是( )
A.求两个正整数的最大公约数
B.求两个正整数的最大值
C.求两个正整数的最小值
D.求圆周率的不足近似值
【分析】由算法程序可知,用辗转相除法求m,n两数的最大公约数,由此可得答案.
【解答】解:由算法程序可知,用辗转相除法求m,n两数的最大公约数,
输出的数为m、n的最大公约数.
故选:A.
【点评】本题考查了直到型循环结构的程序框图,考查了算法案例辗转相除法求m,n两数的最大公约数,读懂程序语言是关键.
11.如程序框图所示,其作用是输入x的值,输出相应的y的值.若要使输入的x的值与输出的y的值相等,则这样的x的值有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是求分段函数的函数值.
【解答】解:这是一个用条件分支结构设计的算法,
该程序框图所表示的算法的作用是求分段函数y=的函数值,
当x≤2时,令x2=x,得x=0或1;
当2<x≤5时,令2x﹣3=x,得x=3;
当x>5时,令=x,得x=±1(舍去),
故只有3个值符合题意.
故选:C.
【点评】根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)?②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.
12.运行如图的程序框图,设输出数据构成的集合为A,从集合A中任取一个元素a,则函数y=xa,x∈[0,+∞)是增函数的概率为( )
A. B. C. D.
【分析】先根据流程图进行逐一进行运行,求出集合A,再求出基本事件的总数,然后讨论满足“函数y=xα,x∈[0,+∞)是增函数”时包含基本事件,最后根据古典概型公式求出该概率即可.
【解答】解:由框图可知A={3,0,﹣1,8,15},
其中基本事件的总数为5,
设集合中满足“函数y=xα,x∈[0,+∞)是增函数”为事件E,
当函数y=xα,x∈[0,+∞)是增函数时,α>0
事件E包含基本事件为3,
则.
故选:C.
【点评】本题主要考查了当型循环结构,以及与集合和古典概型相结合等问题,算法与其他知识结合在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.
二.填空题(共4小题)
13.用二分法求方程x3﹣2x﹣5=0在区间(2,4)上的实数根时,取中点x1=3,则下一个有根区间是 (2,3) .
【分析】构造函数f(x)=x3﹣2x﹣5,确定f(2),f(3),f(4)的符号,根据零点存在定理,即可得到结论.
【解答】解:设函数f(x)=x3﹣2x﹣5,则
∵f(2)=﹣1<0,f(3)=16>0,f(4)=51>0
∴下一个有根区间是(2,3).
故答案为:(2,3).
【点评】本题考查二分法,考查零点存在定理,考查学生的计算能力,属于基础题.
14.函数的一个零点在区间(1,2)内,则实数a的取值范围是 (0,3) .
【分析】由题意可得f(1)f(2)=(0﹣a)(3﹣a)<0,解不等式求得实数a的取值范围.
【解答】解:由题意可得f(1)f(2)=(0﹣a)(3﹣a)<0,
解得:0<a<3,
故实数a的取值范围是(0,3),
故答案为:(0,3)
【点评】本题考查函数零点的定义以及函数零点判定定理的应用,属于基础题.
15.顾客请一位工艺师把A,B两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件原料先由徒弟完成粗加工,再由师傅进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下:
工序时间原料 粗加工 精加工
原料A 9 15
原料B 6 21
则最短交货期为 42 个工作日.
【分析】先完成B的加工,再完成A的加工即可.
【解答】解:由题意,徒弟利用6天完成原料B的加工,由师傅利用21天完成精加工,与此同时,徒弟利用9天完成原料A的加工,最后由师傅利用15天完成精加工,故最短交货期为6+21+15=42 个工作日.
故答案为:42.
【点评】本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,属于基础题.
16.把二进制数1011(2)化成十进制数为 11 .
【分析】欲将二进制数1011用十进制表示,只须根据转换公式:1×23+0×22+1×21+1进行计算即得.
【解答】解:二进制数1011用十进制可以表示为:
1×23+0×22+1×21+1=11.
故答案为:11.
【点评】本题主要考查了算法的概念以及二进制数与用十进制的互化,属于基础题.
三.解答题(共6小题)
17.用秦九韶算法求多项式f(x)=8x7+5x6+3x4+2x+1,当x=2时的值.
【分析】利用秦九韶算法一步一步地代入运算,注意本题中有几项不存在,此时在计算时,我们应该将这些项加上,比如含有x3这一项可看作0?x3.
【解答】解:根据秦九韶算法,把多项式改写成如下形式
f(x)=8x7+5x6+0?x5+3?x4+0?x3+0?x2+2x+1
=((((((8x+5)x+0)x+3)x+0)x+0)x+2)x+1
v0=8,v1=8×2+5=21
v2=21×2+0=42,v3=42×2+3=87
v4=87×2+0=174,v5=174×2+0=348
v6=348×2+2=698,v7=698×2+1=1397.
∴当x=2时,多项式的值为1397.
【点评】一般地,一元n次多项式的求值需要经过次乘法和n次加法,而秦九韶算法只需要n次乘法和n次加法.
18.已知一个5次多项式为f(x)=4x5﹣3x3+2x2+5x+1,用秦九韶算法求这个多项式当x=2时的值.
【分析】把所给的多项式写成关于x的一次函数的形式,依次写出,得到最后结果,从里到外进行运算,得到要求的值.
【解答】解:由f(x)=((((4x+0)x﹣3)x+2)x+5)x+1
∴v0=4
v1=4×2+0=8
v2=8×2﹣3=13
v3=13×2+2=28
v4=28×2+5=61
v5=61×2+1=123
故这个多项式当x=2时的值为123.
【点评】本题考查排序问题与算法的多样性,解答本题,关键是了解秦九韶算法的规则,求出多项式当x=2时的值.
19.请从下面具体的例子中说明几个基本的程序框和它们各自表示的功能,并把它填在相应的括号内.
【分析】在程序框图中,一个或几个程序框的组合表示算法中的一个步骤,带有方向箭头的流程线将程序框连接起来,表示算法的步骤的执行顺序,包括三个基本的逻辑结构.
【解答】解:
【点评】本题考查程序框图的概念,考查程序框图的三种逻辑结构,是一个基础题,从本题的知识点可以掌握本章的知识.
20.下面程序框图输出的S表示什么?虚线框表示什么结构?
【分析】由于圆的面积公式就是πr2,所以判断出输出的S是半径为5的圆面积.由框图三种结构的特点,此框图无判断框,是顺序结构.
【解答】解:由框图知,当r=5时,输出的s=πr2
所以程序框图输出的S表示:求半径为5的圆的面积的算法的程序框图,
虚线框是一个顺序结构.
【点评】本题考查圆的面积公式、考查程序框图中三种结构的特点,并由特点判断出是何种结构.
21.如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值,
(I)请指出该程序框图所使用的逻辑结构;
(Ⅱ)若视x为自变量,y为函数值,试写出函数y=f(x)的解析式;
(Ⅲ)若要使输入的x的值与输出的y的值相等,则输入x的值的集合为多少?
【分析】(I)根据程序框图,可知该程序框图所使用的逻辑结构;
(Ⅱ)利用程序框图,可得分段函数的解析式;
(Ⅲ)利用分段函数,根据使输入的x的值与输出的y的值相等,建立方程,即可求得结论.
【解答】解:(I)程序框图所使用的逻辑结构是条件结构和顺序结构;…(2分)
(Ⅱ)解析式为:f(x)=…(7分)
(Ⅲ)依题意得,或,或,解得x=0,或x=1,或x=3
故所求的集合为{0,1,3}.…(13分)
【点评】本题考查程序框图,考查学生的读图能力,考查学生的计算能力,属于基础题.
22.如图是计算1+2++3++…+2010+的值的程序框图,
(1)图中空白的判断框应填 i≤2010 ?处理框应填 S=S+i+1/i ;
(2)写出与程序框图相对应的程序.
【分析】(1)本题考查的知识点是程序框图,由已知得本程序的作用是计算1+2++3++…+2010+,由于第一次执行循环时的循环变量初值为2,步长为1,最后一次执行循环进循环变量值为2010,我们根据利用循环结构进行累加的方法,不难给出结论.
(2)先判定循环的结构,然后选择对应的循环语句,对照流程图进行逐句写成语句即可.
【解答】解:(1)判断框:i≤2010
或i<2011;…(3分)
执行框:S=S+i+1/i…(6分)
(2)程序:如图…(12分)(全对才给分)
故答案为:i≤2010;S=S+i+1/i.
【点评】算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.
