2018年人教A版必修2《第2章 点、直线、平面之间的位置关系》单元测试卷(解析版)
文档属性
| 名称 | 2018年人教A版必修2《第2章 点、直线、平面之间的位置关系》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-20 09:36:17 | ||
图片预览




文档简介
人教A版必修2《第2章 点、直线、平面之间的位置关系》2018年单元测试卷
一.选择题(共16小题)
1.若一个角的两边分别和另一个角的两边平行,那么这两个角( )
A.相等 B.互补 C.相等或互补 D.无法确定
2.如图,各棱长均为1的正三棱柱ABC﹣A1B1C1,M,N分别为线段A1B,B1C上的动点,且MN∥平面ACC1A1,则这样的MN有( )
A.1条 B.2条 C.3条 D.无数条
3.下列命题正确的个数是( )
①梯形的四个顶点在同一平面内
②三条平行直线必共面
③有三个公共点的两个平面必重合
④每两条相交的且交点各不相同的四条直线一定共面.
A.1个 B.2个 C.3个 D.4个
4.设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是( )
A.若a,b与α所成的角相等,则α∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若a?α,b?β,α∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,是a⊥b
5.已知AB∥PQ,BC∥QR,∠ABC=60°,则∠PQR等于( )
A.60° B.60°或120°
C.120° D.以上结论都不对
6.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
A.在棱AD上存在点M,使AD⊥平面PMB
B.异面直线AD与PB所成的角为90°
C.二面角P﹣BC﹣A的大小为45°
D.BD⊥平面PAC
7.如图,在正方体ABCD﹣A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
A.[,] B.[0,1] C.[,] D.[,]
8.在正方体ABCD﹣A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
①FG∥平面AA1D1D; ②EF∥平面BC1D1;
③FG∥平面BC1D1; ④平面EFG∥平面BC1D1
其中推断正确的序号是( )
A.①③ B.①④ C.②③ D.②④
9.已知点P为△ABC所在平面外一点,点D、E、F分别在直线PA、PB、PC上,平面DEF∥平面ABC,且===,则=( )
A. B. C. D.
10.在底面是菱形的四棱锥P﹣ABCD中,PA⊥底面ABCD,点E为棱PB的中点,点F在棱AD上,平面CEF与PA交于点K,且PA=AB=3,AF=2,则等于( )
A. B. C. D.
11.已知平面α,β所成的二面角为80°,P为α,β外一定点,则过点P作直线与α,β都成30°的直线有( )
A.1条 B.2条 C.3条 D.4条
12.如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( )
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积
13.已知m,n是两条不重合的直线,α,β是不重合的平面,下面四个命题中正确的是( )
A.若m?α,n?β,m⊥n,则α⊥β B.若m∥α,m⊥n,则n⊥α
C.若m⊥α,m⊥β,则α∥β D.若m⊥n,m⊥β,则n∥β
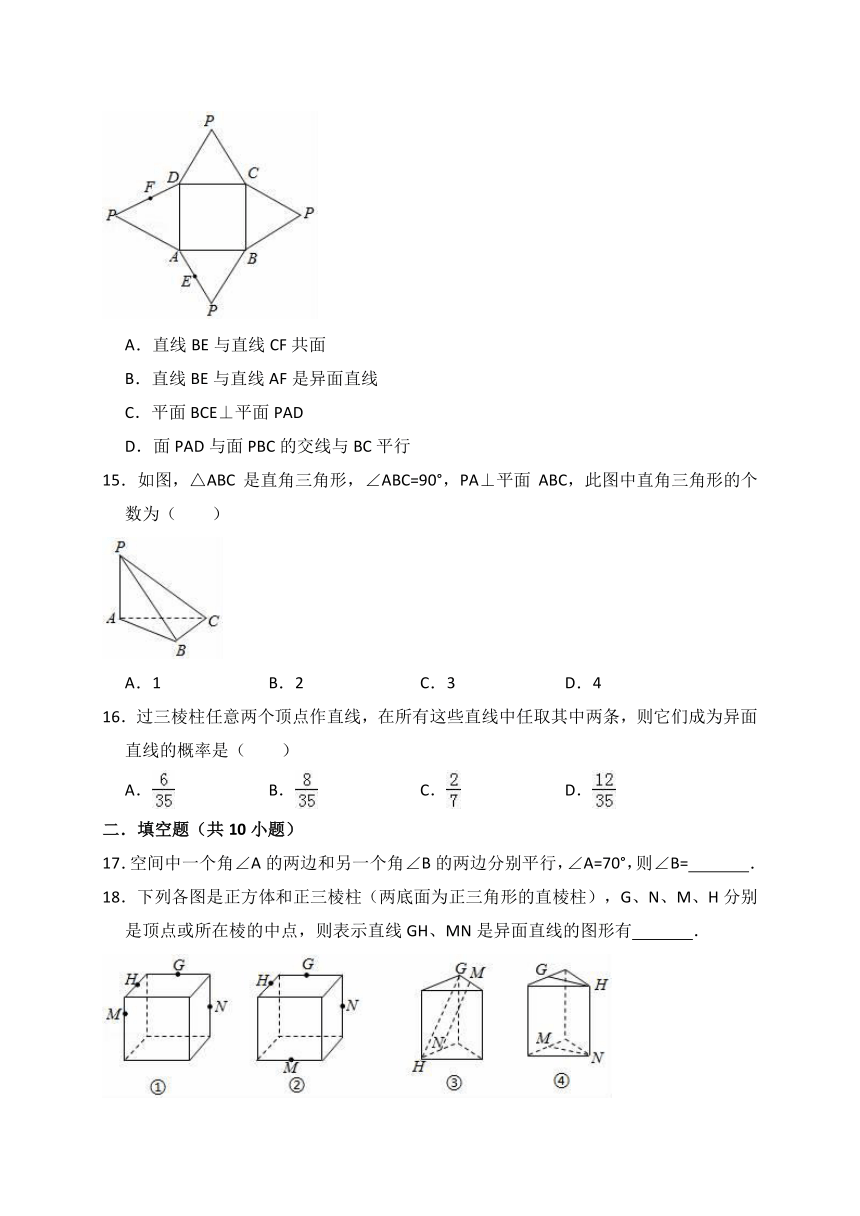
14.如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为( )
A.直线BE与直线CF共面
B.直线BE与直线AF是异面直线
C.平面BCE⊥平面PAD
D.面PAD与面PBC的交线与BC平行
15.如图,△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,此图中直角三角形的个数为( )
A.1 B.2 C.3 D.4
16.过三棱柱任意两个顶点作直线,在所有这些直线中任取其中两条,则它们成为异面直线的概率是( )
A. B. C. D.
二.填空题(共10小题)
17.空间中一个角∠A的两边和另一个角∠B的两边分别平行,∠A=70°,则∠B= .
18.下列各图是正方体和正三棱柱(两底面为正三角形的直棱柱),G、N、M、H分别是顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有 .
19.已知l,m为直线,α为平面,l∥α,m?α,则l与m之间的关系是 .
20.设α和β为不重合的两个平面,给出下列命题:
(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
(2)若α外一条直线l与α内的一条直线平行,则l和α平行;
(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
(4)如果l与α内的两条直线垂直则直线l与α垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
21.如图,在正三棱柱A1B1C1﹣ABC中,AB=2,A1A=2,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为 .
22.已知a,b是一对异面直线,且a,b成70°角.P为空间一定点,则在过P点的直线中与a,b所成角都为70°的直线有 条.
23.“直线l与平面α相交于点P”用集合语言表示为 .
24.在空间平行于同一直线的两条直线的位置关系是 .
25.如图,正方体ABCD﹣A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
①点E到平面ABC1D1的距离为;
②直线BC与平面ABC1D1所成角为45°;
③空间四边形ABCD1在正方体六个面内的射影围成的图形中,面积最小的值为;
④BE与CD1所成角的正弦值为;
⑤二面角A﹣BD1﹣C的大小为.
其中真命题是 .(写出所有真命题的序号)
26.在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为 .
三.解答题(共10小题)
27.已知:a?α,b?α,a∩b=A,P∈b,PQ∥a.求证:PQ?α.
28.正方体六个表面的中心所确定的直线中,异面直线共有多少对?
29.如图,在四棱锥p﹣ABCD中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,AB=1,AD=2,PA=CD=4.
(Ⅰ)求证:BD⊥PC;
(Ⅱ)求二面角B﹣PC﹣A的余弦值.
30.分别用文字语言、图形语言和符号语言书写面面平行的判定定理.
31.已知:四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且==,求证:直线FE、GH、AC交于一点.
32.三棱锥P﹣ABC中,PC=x,其余棱长均为1.
(1)求证:PC⊥AB;
(2)求三棱锥P﹣ABC的体积的最大值.
33.如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求异面直线AE与BC所成角的余弦值;
(Ⅲ)求AD与平面ABE所成角的正弦值.
34.已知E、F、G、H是所在线段上的点,且EH∥FG.
求证:EH∥BD.
35.如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=,E,F分别是BC,A1C的中点.
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, =λ.若CM∥平面AEF,求实数λ的值.
36.如图,在四棱台ABCD﹣A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.
(1)求证:BD⊥C1C;
(2)求证:C1C∥平面A1BD.
人教A版必修2《第2章 点、直线、平面之间的位置关系》2018年单元测试卷
参考答案与试题解析
一.选择题(共16小题)
1.若一个角的两边分别和另一个角的两边平行,那么这两个角( )
A.相等 B.互补 C.相等或互补 D.无法确定
【分析】本题应分两种情况讨论,如图,∠1,∠2,∠3的两边互相平行,由图形可以看出∠1和∠2是邻补角,它们和∠3的关系容易知道一个相等,一个互补.
【解答】解:如图,∠1,∠2,∠3的两边互相平行,
∴∠3=∠4,∠4=∠1,∠4+∠2=180°;
∴∠3=∠1,∠3+∠2=180°.
∴这两个角相等或互补.
故选:C.
【点评】解决本题时要联想的平行线的性质定理,正确认识其基本图形,就不会忽视互补的情况.熟记结论:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
2.如图,各棱长均为1的正三棱柱ABC﹣A1B1C1,M,N分别为线段A1B,B1C上的动点,且MN∥平面ACC1A1,则这样的MN有( )
A.1条 B.2条 C.3条 D.无数条
【分析】任取线段A1B上一点M,过M作MH∥AA1,交AB于H,过H作HG∥AC交BC于G,过G作CC1的平行线,与CB1一定有交点N,且MN∥平面ACC1A1,则这样的MN有无数个.
【解答】解:如图,任取线段A1B上一点M,过M作MH∥AA1,交AB于H,过H作HG∥AC交BC于G,
过G作CC1的平行线,与CB1一定有交点N,且MN∥平面ACC1A1,则这样的MN有无数个.
故选:D.
【点评】不本题考查了空间线面位置关系,转化思想,属于中档题.
3.下列命题正确的个数是( )
①梯形的四个顶点在同一平面内
②三条平行直线必共面
③有三个公共点的两个平面必重合
④每两条相交的且交点各不相同的四条直线一定共面.
A.1个 B.2个 C.3个 D.4个
【分析】对四个命题一一判断,从而确定正确与否.
【解答】解:①梯形的四个顶点在同一平面内,正确;
②三条平行直线必共面不正确,如三棱柱的三条侧棱;
③有三个公共点的两个平面必重合不正确,若三个公共点共线;
④每两条相交的且交点各不相同的四条直线一定共面,正确.
故选:B.
【点评】本题考查了平面中的公理,属于基础题.
4.设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是( )
A.若a,b与α所成的角相等,则α∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若a?α,b?β,α∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,是a⊥b
【分析】根据题意,依次分析选项,A、用直线的位置关系判断.B、用长方体中的线线,线面,面面关系验证.C、用长方体中的线线,线面,面面关系验证.D、由a⊥α,α⊥β,可得到a?β或a∥β,再由b⊥β得到结论.
【解答】解:A、直线a,b的方向相同时才平行,不正确;
B、用长方体验证.如图,设A1B1为a,平面AC为α,BC为b,平面A1C1为β,显然有a∥α,b∥β,α∥β,但得不到a∥b,不正确;
C、可设A1B1为a,平面AB1为α,CD为b,平面AC为β,满足选项C的条件却得不到α∥β,不正确;
D、∵a⊥α,α⊥β,
∴a?β或a∥β
又∵b⊥β
∴a⊥b
故选:D.
【点评】本题主要考查空间内两直线,直线与平面,平面与平面间的位置关系,综合性强,方法灵活,属中档题.
5.已知AB∥PQ,BC∥QR,∠ABC=60°,则∠PQR等于( )
A.60° B.60°或120°
C.120° D.以上结论都不对
【分析】首先,直接根据平行关系求解即可.
【解答】解:∵AB∥PQ,BC∥QR,
且∠ABC=60°,
∴∠PQR=60°或120°
故选:B.
【点评】本题重点考查了平面的性质、平行关系运用.属于中档题.
6.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
A.在棱AD上存在点M,使AD⊥平面PMB
B.异面直线AD与PB所成的角为90°
C.二面角P﹣BC﹣A的大小为45°
D.BD⊥平面PAC
【分析】根据线面垂直,异面直线所成角的大小以及二面角的求解方法分别进行判断即可.
【解答】解:对于A,取AD的中点M,连PM,BM,则∵侧面PAD为正三角形,
∴PM⊥AD,
又底面ABCD是∠DAB=60°的菱形,
∴三角形ABD是等边三角形,
∴AD⊥BM,
∴AD⊥平面PBM,故A正确,
对于B,∵AD⊥平面PBM,
∴AD⊥PB,即异面直线AD与PB所成的角为90°,故B正确,
对于C,∵底面ABCD为菱形,∠DAB=60°平面PAD⊥平面ABCD,
∴BM⊥BC,则∠PBM是二面角P﹣BC﹣A的平面角,
设AB=1,则BM=,PM=,
在直角三角形PBM中,tan∠PBM=,
即∠PBM=45°,故二面角P﹣BC﹣A的大小为45°,故C正确,
故错误的是D,
故选:D.
【点评】本题主要考查空间直线和平面位置关系以及二面角的求解,根据相应的判断和证明方法是解决本题的关键.综合性较强,难度较大.
7.如图,在正方体ABCD﹣A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
A.[,] B.[0,1] C.[,] D.[,]
【分析】如图所示,作出平面MNQB1∥平面DEF,A1Q=2AQ,D1N=2ND,P的轨迹是线段QN,P在Q处,tan∠ABP=,P在N处,tan∠ABP==,即可得出结论.
【解答】解:如图所示,作出平面MNQB1∥平面DEF,则A1Q=2AQ,D1N=2ND,
∵PB1∥平面DEF,∴P的轨迹是线段QN.
P在Q处,tan∠ABP=,P在N处,tan∠ABP==,
故选:D.
【点评】本题考查线面、面面平行,考查线面角,考查学生分析解决问题的能力,属于中档题.
8.在正方体ABCD﹣A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
①FG∥平面AA1D1D; ②EF∥平面BC1D1;
③FG∥平面BC1D1; ④平面EFG∥平面BC1D1
其中推断正确的序号是( )
A.①③ B.①④ C.②③ D.②④
【分析】由FG∥BC1,BC1∥AD1,得FG∥AD1,从而FG∥平面BC1D1,FG∥平面AA1D1D;由EF∥A1C1,A1C1与平面BC1D1相交,从而EF与平面BC1D1相交,进而平面EFG与平面BC1D1相交.
【解答】解:∵在正方体ABCD﹣A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,
∴FG∥BC1,∵BC1∥AD1,∴FG∥AD1,
∵FG?平面AA1D1D,AD1?平面AA1D1D,∴FG∥平面AA1D1D,故①正确;
∵EF∥A1C1,A1C1与平面BC1D1相交,∴EF与平面BC1D1相交,故②错误;
∵E,F,G分别是A1B1,B1C1,BB1的中点,
∴FG∥BC1,∵FG?平面BC1D1,BC1?平面BC1D1,
∴FG∥平面BC1D1,故③正确;
∵EF与平面BC1D1相交,∴平面EFG与平面BC1D1相交,故④错误.
故选:A.
【点评】本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.
9.已知点P为△ABC所在平面外一点,点D、E、F分别在直线PA、PB、PC上,平面DEF∥平面ABC,且===,则=( )
A. B. C. D.
【分析】根据题意得到△DEF∽△ABC,则相似三角形的面积之比等于相似比的平方.
【解答】解:如图,∵平面DEF∥平面ABC,
∴△DEF∽△ABC,DE∥AB,EF∥BC,DF∥AC,
∴=.
又===,
∴=,
∴==,
∴=()2=.
故选:B.
【点评】本题考查了平面与平面平行的性质:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
10.在底面是菱形的四棱锥P﹣ABCD中,PA⊥底面ABCD,点E为棱PB的中点,点F在棱AD上,平面CEF与PA交于点K,且PA=AB=3,AF=2,则等于( )
A. B. C. D.
【分析】如图所示,延长BA,CF,交于G,连接EG,与PA交于K,则AG=6,过A做AH∥PB,与EG交于H,则==,即可得出结论.
【解答】解:如图所示,延长BA,CF,交于G,连接EG,与PA交于K,则AG=6,
过A做AH∥PB,与EG交于H,则====,
故选:A.
【点评】本题考查棱锥的结构特征,考查平面与平面交线的求法,属于中档题.
11.已知平面α,β所成的二面角为80°,P为α,β外一定点,则过点P作直线与α,β都成30°的直线有( )
A.1条 B.2条 C.3条 D.4条
【分析】过P作平面A垂直于α、β的交线l,并且交l于点0,连接PO,则PO垂直于l,过点P在A内做OP的垂线L',以PO为轴在垂直于PO的平面内转动L',根据三垂线定理可得有两条直线满足题意.以P点为轴在平面A内前后转动L',根据三垂线定理可得也有两条直线满足题意.
【解答】解:首先给出下面两个结论
①两条平行线与同一个平面所成的角相等.
②与二面角的两个面成等角的直线在二面角的平分面上.
图1.
(1)如图1,过二面角α﹣l﹣β内任一点作棱l的垂面AOB,交棱于点O,与两半平面于OA,OB,则∠AOB为二面角α﹣l﹣β的平面角,∠AOB=80°
设OP1为∠AOB的平分线,则∠P1OA=∠P1OB=40°,与平面α,β所成的角都是30°,此时过P且与OP1平行的直线符合要求,当OP1以O为轴心,在二面角α﹣l﹣β的平分面上转动时,OP1与两平面夹角变小,会对称的出现两条符合要求成30°情形.
图2.
(2)如图2,设OP2为∠AOB的补角∠AOB′的平分线,则∠P2OA=∠P2OB=50°,与平面α,β所成的角都是50°.当OP2以O为轴心,在二面角α﹣l﹣β′的平分面上转动时,
OP2与两平面夹角变小,对称地在图中OP2两侧会出现30°情形,有两条.此时过P且与OP2平行的直线符合要求,有两条.
综上所述,直线的条数共有4条.
故选:D.
【点评】本题主要考查线面角,以及考查解决线面角的特殊方法的应用,考查空间想象能力,体现了转化的思想和运动变化的思想方法,此题是个难题.
12.如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( )
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积
【分析】A.由于平面QEF即为对角面A1B1CD,点P为A1D1的中点,可得:点P到平面QEF即到对角面A1B1CD的距离=为定值;
D.由于点Q到直线CD的距离是定值a,|EF|为定值,因此△QEF的面积=为定值;
C.由A.D可知:三棱锥P﹣QEF的体积为定值;
B.用排除法即可得出.
【解答】解:A.∵平面QEF即为对角面A1B1CD,点P为A1D1的中点,∴点P到平面QEF即到对角面A1B1CD的距离=为定值;
D.∵点Q到直线CD的距离是定值a,|EF|为定值,∴△QEF的面积=为定值;
C.由A.D可知:三棱锥P﹣QEF的体积为定值;
B.直线PQ与平面PEF所成的角与点Q的位置有关系,因此不是定值,或用排除法即可得出.
综上可得:只有B中的值不是定值.
故选:B.
【点评】本题综合考查了正方体的性质、三棱锥的体积、点到平面的距离、异面直线所成的角等基础知识与基本技能方法,考查了推理能力和空间想象能力,属于难题.
13.已知m,n是两条不重合的直线,α,β是不重合的平面,下面四个命题中正确的是( )
A.若m?α,n?β,m⊥n,则α⊥β B.若m∥α,m⊥n,则n⊥α
C.若m⊥α,m⊥β,则α∥β D.若m⊥n,m⊥β,则n∥β
【分析】在A中,α与β相交或平行;在B中,n与α相交、平行或n?α;在C中,由面面平行的判定定理得α∥β;在D中,n∥β或n?β.
【解答】解:由m,n是两条不重合的直线,α,β是不重合的平面,知:
在A中:若m?α,n?β,m⊥n,则α与β相交或平行,故A错误;
在B中:若m∥α,m⊥n,则n与α相交、平行或n?α,故B错误;
在C中:若m⊥α,m⊥β,则由面面平行的判定定理得α∥β,故C正确;
在D中:若m⊥n,m⊥β,则n∥β或n?β,故D错误.
故选:C.
【点评】本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.
14.如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为( )
A.直线BE与直线CF共面
B.直线BE与直线AF是异面直线
C.平面BCE⊥平面PAD
D.面PAD与面PBC的交线与BC平行
【分析】几何体的展开图,复原出几何体,利用异面直线的定义判断A,B的正误;
利用直线与平面垂直的判定定理判断C的正误;利用直线与平面平行的判定、性质定理判断D的正误.
【解答】解:画出几何体的图形,如图,
由题意可知,A,直线BE与直线CF共面,正确,
因为E,F是PA与PD的中点,可知EF∥AD,
所以EF∥BC,直线BE与直线CF是共面直线;
B,直线BE与直线AF异面;满足异面直线的定义,正确.
C,因为△PAB是等腰三角形,BE与PA的关系不能确定,所以平面BCE⊥平面PAD,不正确.
D,∵AD∥BC,∴AD∥平面PBC,∴面PAD与面PBC的交线与BC平行,正确.
故选:C.
【点评】本题是中档题,考查空间图形中直线与直线、平面的位置关系,考查异面直线的判断,基本知识与定理的灵活运用.
15.如图,△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,此图中直角三角形的个数为( )
A.1 B.2 C.3 D.4
【分析】推导出AB⊥BC,PA⊥BC,从而BC⊥平面PAB,由此能求出图中直角三角形的个数.
【解答】解:∵△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,
∴AB⊥BC,PA⊥BC,
∵AB∩PA=A,∴BC⊥平面PAB,
∴图中直角三角形有△ABC(∠ABC是直角 ),
△PAC(∠PAC是直角),△PAB(∠PAB是直角),△PBC(∠PBC是直角),
∴图中直角三角形有4个.
故选:D.
【点评】本题考查几何体中直角三角形的个数的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、考查函数与方程思想、数形结合思想,是基础题.
16.过三棱柱任意两个顶点作直线,在所有这些直线中任取其中两条,则它们成为异面直线的概率是( )
A. B. C. D.
【分析】先求出总共可以做多少直线,然后通过分类找出能成为异面直线的数量,最后二者相比求概率即可
【解答】解:从三棱柱的六个顶点中任取两点作直线,可做直线条
从这15条直线中任取两条,共种
其中成异面直线可分为以下几类:
(1)侧棱与底面边:有3×2=6对
(2)侧棱与侧面对角线:有3×2=6对
(3)底面边与侧面对角线:有3×2+3×2=6+6=12对
(4)底面边与底面边:有3×2=6对
(5)侧面对角线与侧面对角线:对
共6+6+12+6+6=36对
∴两直线为异面直线的概率为:
故选:D.
【点评】本题考查异面直线的判定和等可能事件的概率,要求弄精确分类.分类较容易出错,每一类中比较容易重复或遗漏.要有较强的空间想象力和观察力.属较难题
二.填空题(共10小题)
17.空间中一个角∠A的两边和另一个角∠B的两边分别平行,∠A=70°,则∠B= 70°或110° .
【分析】由空间两条平行线的性质和等角定理,可得∠B与∠A相等或∠B与∠A互补,由此不难得到正确答案.
【解答】解:①若角∠A的两边和角∠B的两边分别平行,且方向相同,则∠A与∠B相等
此时∠B=∠A=70°;
②当角∠A的两边和角∠B的两边分别平行,且一边方向相同另一边方向相反,则∠A与∠B互补,
此时∠B=180°﹣∠A=110°.
故答案为:70°或110°
【点评】本题给出空间一个角的两边分别与另一个角的两边平行,求它们之间的度数关系,考查了空间两条平行线的性质和等角定理等知识,属于基础题.
18.下列各图是正方体和正三棱柱(两底面为正三角形的直棱柱),G、N、M、H分别是顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有 ③ .
【分析】根据已知中的图形,结合棱柱的几何特征及异面直线的判定定理,逐一分析直线GH、MN的位置关系,可得答案.
【解答】解:①中GH∥MN,GH=MN,故不满足条件;
②中G、N、M、H四点在如图所示的平面中,
故不满足条件;
③中,GH?左侧面,MN∩左侧面=N,N?GH,
故直线GH、MN是异面直线,
④中,GH∥MN,故不满足条件,
故答案为:③.
【点评】本题考查的知识点是棱柱的几何特征及异面直线的判定定理,难度中档.
19.已知l,m为直线,α为平面,l∥α,m?α,则l与m之间的关系是 平行或异面 .
【分析】以正方体为载体,列举出所有情况,能求出两直线间的关系.
【解答】解:在正方体ABCD﹣A1B1C1D1中,
A1B1∥平面ABCD,AB?平面ABCD,BC?平面ABCD,
A1B1与AB平行,A1B1与BC异面,
∴l,m为直线,α为平面,l∥α,m?α,
则l与m之间的关系是平行或异面.
故答案为:平行或异面.
【点评】本题考查两直线间的位置关系的判断,考查空间中空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想,属于中档题.
20.设α和β为不重合的两个平面,给出下列命题:
(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
(2)若α外一条直线l与α内的一条直线平行,则l和α平行;
(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
(4)如果l与α内的两条直线垂直则直线l与α垂直.
上面命题中,真命题的序号 ①② (写出所有真命题的序号).
【分析】在①中,由面面平行的判定定理得α平行于β;在②中,由线面平行的判定定理得l和α平行;在③中,α与β所成的角可能是锐角,也可能是直角,也可能是钝角;在④中,只有l与α内的两条相交直线垂直,才有直线与α垂直.
【解答】解:由设α,β为不重合的两个平面,知:
在①中,若α内的两条相交直线分别平行于β内的两条直线,则由面面平行的判定定理得α平行于β,故①正确;
在②中,若α外一条直线l与α内的一条直线平行,则由线面平行的判定定理得l和α平行,故②正确;
在③中,设α和β相交于直线l,若α内有一条直线垂直于l,则α与β所成的角可能是锐角,也可能是直角,也可能是钝角,故③错误;
在④中,只有l与α内的两条相交直线垂直,才有直线与α垂直,故④错误.
故答案为:①②.
【点评】本题考查命题真假的判断,考查空间中线线、线面、面面的位置关系等基础知识,考查学生分析解决问题的能力,是中档题.
21.如图,在正三棱柱A1B1C1﹣ABC中,AB=2,A1A=2,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为 +2 .
【分析】由正三棱柱A1B1C1﹣ABC的性质可得:AA1⊥AB,AA1⊥AC.在Rt△ADF中,利用勾股定理可得DF=2.因此只要求出DE+EF的最小值即可得出.把底面ABC展开与侧面ACC1A1在同一个平面,如图所示,只有当三点D,E,F在同一条直线时,DE+EF取得最小值.利用余弦定理即可得出.
【解答】解:由正三棱柱A1B1C1﹣ABC,可得AA1⊥底面ABC,∴AA1⊥AB,AA1⊥AC.
在Rt△ADF中,DF==2.
把底面ABC展开与侧面ACC1A1在同一个平面,如图所示,
只有当三点D,E,F在同一条直线时,DE+EF取得最小值.
在△ADE中,∠DAE=60°+90°=150°,由余弦定理可得:
DE==.
∴△DEF周长的最小值=+2.
故答案为: +2.
【点评】本题考查了空间几何位置关系、余弦定理、侧面展开图,考查了转化能力、数形结合能力、推理能力与计算能力,属于难题.
22.已知a,b是一对异面直线,且a,b成70°角.P为空间一定点,则在过P点的直线中与a,b所成角都为70°的直线有 4 条.
【分析】如图所示,α∥β,a?α,b?β.任取P∈B,过点P作a′∥a,则a′?β.过点P可作PA满足与直线a′,b所成角都为70°的直线,其中PA在∠MPN的上方.同理可以作出其它3条,当点P不在其中一条直线上时,可以通过平移两条异面直线即可.
【解答】解:如图所示,
α∥β,a?α,b?β.
?P∈β,过点P作a′∥a,则a′?β.
过点P可作PA满足与直线a′,b所成角都为70°的直线,其中PA在∠MPN的上方.
同理可以作出其它3条,PB,PC,PD(∵70°+70°>110°).
当点P不在其中一条直线上时,可以通过平移两条异面直线即可.
综上可得:在过P点的直线中与a,b所成角都为70°的直线有4条.
故答案为:4.
【点评】本题考查了异面直线所成的夹角、平移变换、分类讨论方法等基础知识与基本技能方法,考查了推理能力和空间想象能力,属于难题.
23.“直线l与平面α相交于点P”用集合语言表示为 l∩α=P .
【分析】利用空间线面关系对应的符号语言表示出来.
【解答】解:直线l与平面α相交于点P,用集合语言表示为l∩α=P;
故答案为:l∩α=P.
【点评】本题考查了平面与直线位置关系的集合表示;属于基础题.
24.在空间平行于同一直线的两条直线的位置关系是 平行 .
【分析】根据平行公理可以证明.
【解答】解:根据平行公理可知:在空间平行于同一直线的两条直线的位置关系是平行的.
故答案为:平行.
【点评】本题主要考查空间直线的位置关系的判断,利用平行公理是解决本题的关键,比较基础.
25.如图,正方体ABCD﹣A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
①点E到平面ABC1D1的距离为;
②直线BC与平面ABC1D1所成角为45°;
③空间四边形ABCD1在正方体六个面内的射影围成的图形中,面积最小的值为;
④BE与CD1所成角的正弦值为;
⑤二面角A﹣BD1﹣C的大小为.
其中真命题是 ②③④ .(写出所有真命题的序号)
【分析】对5个命题分别进行判断,即可得出结论.
【解答】解:①由于A1B1∥平面ABC1D1,故B1到平面ABC1D1的距离即点E到平面ABC1D1的距离,
连接B1C交BC1于F,则易得B1F垂直于平面ABC1D1,而B1F=,故点E到平面ABC1D1的距离为,故①错;
②易得B1C垂直于平面ABC1D1,故∠CBC1为直线BC与平面ABC1D1所成的角,且为45°,故②正确;
③易得空间四边形ABCD1在正方体的面ABCD、面A1B1C1D1内的射影面积为1,在面BB1C1C内、面AA1D1D内的射影面积为,在面ABB1A1内、面CC1D1D内的射影面积为,故③正确;
④BE与CD1所成的角,即为BA1与BE所成角,即为∠A1BE,A1E=,BE=,BA1=,cos∠A1BE==,sin∠A1BE=,故④正确;
⑤在直角三角形BAD1中过A作AH垂直于BD1,连接CH,易知CH垂直于BD1,故∠AHC是二面角A﹣BD1﹣C的平面角,由余弦定理得,cos∠AHC==﹣,故∠AHC=,故⑤错.
故答案为:②③④
【点评】本题考查命题的真假判断,考查空间线面位置关系,考查空间角,考查学生分析解决问题的能力,知识综合性强.
26.在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为 [10°,50°] .
【分析】平移CB1到A处,由已知得∠B1CA=30°,∠B1AC=150°,0≤∠C1AC≤20°,由此能求出直线B1C与直线AC1所成角的取值范围.
【解答】解:∵在△ABC中,∠BAC=10°,∠ACB=30°,
将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,
如图,平移CB1到A处,B1C绕AC旋转,
∴∠B1CA=30°,∠B1AC=150°,
AC1绕AB旋转,∴0°≤∠C1AC≤2∠CAB,
∴0≤∠C1AC≤20°,
设直线B1C与直线AC1所成角为α,
则∠B1AC﹣∠C1AC≤α≤∠B1AC+∠C1AC,
∵130°≤∠B1AC﹣∠C1AC≤150°,
150°≤∠B1AC+∠C1AC≤170°,
∴10°≤α≤50°或130°≤α≤170°(舍).
故答案为:[10°,50°].
【点评】本题考查两直线所成角的取值的求法,解题时要认真审题,注意旋转性质的合理运用,是难题.
三.解答题(共10小题)
27.已知:a?α,b?α,a∩b=A,P∈b,PQ∥a.求证:PQ?α.
【分析】首先根据两条直线平行,得到一个确定的平面,根据直线a?β,点P∈β,p∈b,b?α,确定p∈α,根据一条直线和直线外一点可以确定一个平面,得到另个平面是同一个平面,得到结论.
【解答】证明∵PQ∥a,
∴PQ与a确定一个平面β,
∴直线a?β,点P∈β.
∵p∈b,b?α,
∴p∈α
∵a?α,
∴α与β重合,
∴PQ?α
【点评】本题主要考查用平面公理和推论证明共面问题的方法,考查两条平行线确定一个平面,考查两条相交线确定一个平面,考查用同一法证明两个平面重合,实际上这种利用公理证明问题的题目,比较抽象.
28.正方体六个表面的中心所确定的直线中,异面直线共有多少对?
【分析】根据图形结构的对称性,先求出对每一条边,与其异面的边有4个,共有多不对异面直线,再求出每一条边与相对顶点连线中的1条异面,共有多少对异面直线,由此能求出结果.
【解答】解:根据图形结构的对称性,
对每一条边,与其异面的边有4个,共=24对异面直线,
每一条边与相对顶点连线中的1条异面,共有12对异面直线,
综上,正方体六个表面的中心所确定的直线中,异面直线共有36对.
【点评】本题考查满足条件的异面直线有多少对的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.
29.如图,在四棱锥p﹣ABCD中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,AB=1,AD=2,PA=CD=4.
(Ⅰ)求证:BD⊥PC;
(Ⅱ)求二面角B﹣PC﹣A的余弦值.
【分析】(1)以A为原点,建立如图所示空间直角坐标系,求出与的坐标,利用它们的数量积为零证得BD⊥OC;
(2)易证为面PAC的法向量,求出面PBC的法向量,然后求出两法向量的夹角,利用两平面的法向量的夹角与二面角的平面角相等或互补,即可求得二面角B﹣PC﹣A的余弦值.
【解答】证明:(Ⅰ)以A为原点,建立如图所示空间直角坐标系,
则B(0,1,0),C(﹣2,4,0),D(﹣2,0,0),P(0,0,4),
∴,,
∴
所以PC⊥BD.
(Ⅱ)易证为面PAC的法向量,
设面PBC的法向量n=(a,b,c),
所以?
所以面PBC的法向量n=(6,4,1),
∴cosθ=﹣.
因为面PAC和面PBC所成的角为锐角,
所以二面角B﹣PC﹣A的余弦值为.
【点评】本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.
30.分别用文字语言、图形语言和符号语言书写面面平行的判定定理.
【分析】面面平行判定定理的内容用文字叙述、图形语言以及几何符号表示,分别写出即可.
【解答】解:面面平行的判定定理;
(1)文字语言是“如果两个一个平面内有两个相交直线与另一个平面平行,则这两个平面平行”;
(2)图形语言表示:如图所示:
(3)用符号语言表示: ?α∥β.
【点评】本题考查了平面与平面平行的判定定理,熟练掌握平面平行的判定定理是解答本题的关键,是基础题.
31.已知:四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且==,求证:直线FE、GH、AC交于一点.
【分析】证明四边形EFGH是梯形,得出EF,HG相交于一点,再利用面面相交即可证明直线FE、GH、AC交于一点.
【解答】证明:连接BD,∵E,H分别是边AB,AD的中点,
∴EH∥BD;…(2分)
又∵==,∴FG∥BD;…(4分)
因此EH∥FG且EH≠FG;…(6分)
故四边形EFGH是梯形;
所以EF,HG相交,设EF∩HG=K,…(8分)
∵K∈EF,EF?平面ABC,
∴K∈平面ABC;
同理K∈平面ACD,…(10分)
又平面ABC∩平面ACD=AC,∴K∈AC,
故直线FE、GH、AC交于一点.…(12分)
【点评】本题考查了证明三线相交的应用问题,通常是先证明两线交于一点,再证第三条直线过交点即可.
32.三棱锥P﹣ABC中,PC=x,其余棱长均为1.
(1)求证:PC⊥AB;
(2)求三棱锥P﹣ABC的体积的最大值.
【分析】(1)取AB中点M,由△PAB与△CAB均为正三角形,知AB⊥PM,AB⊥CM,由此能够证明AB⊥PC.
(2)当PM⊥平面ABC时,三棱锥的高为PM,由此能求出三棱锥P﹣ABC的体积的最大值.
【解答】解:(1)取AB中点M,
∵△PAB与△CAB均为正三角形,
∴AB⊥PM,AB⊥CM,
∴AB⊥平面PCM,
∴AB⊥PC.
(2)当PM⊥平面ABC时,
三棱锥的高为PM,
此时.
【点评】本题考查PC⊥AB的证明和求三棱锥P﹣ABC的体积的最大值.解题时要认真审题,仔细解答,注意合理地进行等价转化.
33.如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求异面直线AE与BC所成角的余弦值;
(Ⅲ)求AD与平面ABE所成角的正弦值.
【分析】(Ⅰ)先利用P、Q分别是AE、AB的中点?PQ∥BE,PQ=,再利用DC∥BE,DC=可以推出PQ∥DC进而证明PQ∥平面ACD;
(Ⅱ)取BE的中点F,可以先推出QF∥AE且QF=AE,所以∠DFQ就是异面直线AE与BC所成的角,然后在△DFQ中求出
∠DFQ的余弦值即可.
(Ⅲ)由AC=BC和Q为AB的中点可得CQ⊥AB,再利用DC⊥平面ABC,可得CQ⊥平面ABE,进而推出DP⊥平面ABE,所以∠DAP就是AD与平面ABE所成的角,在△DAP中求出∠DAP即可.
【解答】解:(Ⅰ)证明:由已知:P、Q分别是AE、AB的中点,
所以,PQ∥BE,PQ=BE,
又DC∥BE,DC=BE
所以,PQ∥DC
所以,PQ∥平面ACD(4分)
(Ⅱ)取BE的中点F,连接QF,DF,DQ,可以推出QF∥AE且QF=AE,
易证∠DFQ就是异面直线AE与BC所成的角
易知CQ=1,AB=2,AE=4,QF=2,DF=BC=2,DQ=
由余弦定理:可得cos∠DFQ=(8分)
(Ⅲ)由AC=BC和Q为AB的中点可得CQ⊥AB,
再利用DC⊥平面ABC,可得CQ⊥平面ABE,进而推出DP⊥平面ABE
所以∠DAP就是AD与平面ABE所成的角
DP=CQ=1,AD=
所以AD与平面ABE所成角的正弦值为.(12分)
【点评】本题涉及了线面平行以及线线所成角和线面所成角,是对立体几何知识的综合考查.在证明线面平行时,其常用方法是在平面内找已知直线平行的直线.当然也可以用面面平行来推导线面平行.
34.已知E、F、G、H是所在线段上的点,且EH∥FG.
求证:EH∥BD.
【分析】根据一条直线在平面上,一条直线与这条直线平行,根据这两个条件得到直线与平面平行,根据线与面平行的性质,得到线与线平行,得到结论.
【解答】证明:∵点E、F、G、H为空间四边形边AB、BC、CD、DA上的点
∴直线EH?平面BCD,直线FG?平面BCD
又EH∥FG
∴直线EH∥平面BCD
又∵EH?平面ABD且平面ABD∩平面BCD=BD
∴EH∥BD
【点评】本题考查线与面平行的判断,线与面平行的性质,考查线面平行的判定和性质的综合应用,本题是一个考查知识点比较集中的题目,只考线与面的平行,是一个目标很明确的题目.
35.如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=,E,F分别是BC,A1C的中点.
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, =λ.若CM∥平面AEF,求实数λ的值.
【分析】(1)建立坐标系,求出直线的向量坐标,利用夹角公式求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, =λ.求出平面AEF的法向量,利用CM∥平面AEF,即可求实数λ的值.
【解答】解:因为四棱柱ABCD﹣A1B1C1D1为直四棱柱,
所以A1A⊥平面ABCD.
又AE?平面ABCD,AD?平面ABCD,
所以A1A⊥AE,A1A⊥AD.
在菱形ABCD中∠ABC=,则△ABC是等边三角形.
因为E是BC中点,所以BC⊥AE.
因为BC∥AD,所以AE⊥AD.
建立空间直角坐标系.则A(0,0,0),C(,1,0),D(0,2,0),
A1(0,0,2),E(,0,0),F(,,1).
(1)=(0,2,0),=(﹣,,1),
所以异面直线EF,AD所成角的余弦值为=. …(4分)
(2)设M(x,y,z),由于点M在线段A1D上,且=λ,
则(x,y,z﹣2)=λ(0,2,﹣2).
则M(0,2λ,2﹣2λ),=(﹣,2λ﹣1,2﹣2λ). …(6分)
设平面AEF的法向量为=(x0,y0,z0).
因为=(,0,0),=(,,1),
由,得x0=0, y0+z0=0.
取y0=2,则z0=﹣1,
则平面AEF的一个法向量为n=(0,2,﹣1). …(8分)
由于CM∥平面AEF,则=0,即2(2λ﹣1)﹣(2﹣2λ)=0,解得λ=.…(10分)
【点评】本题考查线面角,考查线面平行的运用,考查向量知识的运用,属于中档题.
36.如图,在四棱台ABCD﹣A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.
(1)求证:BD⊥C1C;
(2)求证:C1C∥平面A1BD.
【分析】(1)由AA1⊥平面ABCD,可证AA1⊥BD.四边形ABCD是菱形可得AC⊥BD,由线面垂直的判定定理可证BD⊥面ACC1A1,再由线面垂直的性质定理可证BD⊥CC1.
(2)连接AC和A1C1,设AC∩BD=E,先证明四边形ECC1A1为平行四边形,可得CC1∥A1E,再由线面平行的判定定理可证CC1∥平面A1BD.
【解答】证明:(1)∵AA1⊥平面ABCD,
∴AA1⊥BD.
∵四边形ABCD是菱形,∴AC⊥BD,
又 AC∩AA1=A,∴BD⊥面ACC1A1.
由CC1?面ACC1A1,
∴BD⊥CC1.
(2)连接AC和A1C1,设 AC∩BD=E,由于底面ABCD是平行四边形,故E为平行四边形ABCD的
中心,由棱台的定义及AB=2AD=2A1B1,可得 EC∥A1C1,且 EC=A1C1,
故ECC1A1为平行四边形,∴CC1∥A1E,而CC1?平面A1BD,A1E?平面A1BD,
∴CC1∥平面A1BD.
【点评】本题考查线面平行、垂直的判定定理、线面平行、垂直的性质定理的应用,体现了数形结合的数学思想,属于中档题.
一.选择题(共16小题)
1.若一个角的两边分别和另一个角的两边平行,那么这两个角( )
A.相等 B.互补 C.相等或互补 D.无法确定
2.如图,各棱长均为1的正三棱柱ABC﹣A1B1C1,M,N分别为线段A1B,B1C上的动点,且MN∥平面ACC1A1,则这样的MN有( )
A.1条 B.2条 C.3条 D.无数条
3.下列命题正确的个数是( )
①梯形的四个顶点在同一平面内
②三条平行直线必共面
③有三个公共点的两个平面必重合
④每两条相交的且交点各不相同的四条直线一定共面.
A.1个 B.2个 C.3个 D.4个
4.设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是( )
A.若a,b与α所成的角相等,则α∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若a?α,b?β,α∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,是a⊥b
5.已知AB∥PQ,BC∥QR,∠ABC=60°,则∠PQR等于( )
A.60° B.60°或120°
C.120° D.以上结论都不对
6.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
A.在棱AD上存在点M,使AD⊥平面PMB
B.异面直线AD与PB所成的角为90°
C.二面角P﹣BC﹣A的大小为45°
D.BD⊥平面PAC
7.如图,在正方体ABCD﹣A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
A.[,] B.[0,1] C.[,] D.[,]
8.在正方体ABCD﹣A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
①FG∥平面AA1D1D; ②EF∥平面BC1D1;
③FG∥平面BC1D1; ④平面EFG∥平面BC1D1
其中推断正确的序号是( )
A.①③ B.①④ C.②③ D.②④
9.已知点P为△ABC所在平面外一点,点D、E、F分别在直线PA、PB、PC上,平面DEF∥平面ABC,且===,则=( )
A. B. C. D.
10.在底面是菱形的四棱锥P﹣ABCD中,PA⊥底面ABCD,点E为棱PB的中点,点F在棱AD上,平面CEF与PA交于点K,且PA=AB=3,AF=2,则等于( )
A. B. C. D.
11.已知平面α,β所成的二面角为80°,P为α,β外一定点,则过点P作直线与α,β都成30°的直线有( )
A.1条 B.2条 C.3条 D.4条
12.如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( )
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积
13.已知m,n是两条不重合的直线,α,β是不重合的平面,下面四个命题中正确的是( )
A.若m?α,n?β,m⊥n,则α⊥β B.若m∥α,m⊥n,则n⊥α
C.若m⊥α,m⊥β,则α∥β D.若m⊥n,m⊥β,则n∥β
14.如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为( )
A.直线BE与直线CF共面
B.直线BE与直线AF是异面直线
C.平面BCE⊥平面PAD
D.面PAD与面PBC的交线与BC平行
15.如图,△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,此图中直角三角形的个数为( )
A.1 B.2 C.3 D.4
16.过三棱柱任意两个顶点作直线,在所有这些直线中任取其中两条,则它们成为异面直线的概率是( )
A. B. C. D.
二.填空题(共10小题)
17.空间中一个角∠A的两边和另一个角∠B的两边分别平行,∠A=70°,则∠B= .
18.下列各图是正方体和正三棱柱(两底面为正三角形的直棱柱),G、N、M、H分别是顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有 .
19.已知l,m为直线,α为平面,l∥α,m?α,则l与m之间的关系是 .
20.设α和β为不重合的两个平面,给出下列命题:
(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
(2)若α外一条直线l与α内的一条直线平行,则l和α平行;
(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
(4)如果l与α内的两条直线垂直则直线l与α垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
21.如图,在正三棱柱A1B1C1﹣ABC中,AB=2,A1A=2,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为 .
22.已知a,b是一对异面直线,且a,b成70°角.P为空间一定点,则在过P点的直线中与a,b所成角都为70°的直线有 条.
23.“直线l与平面α相交于点P”用集合语言表示为 .
24.在空间平行于同一直线的两条直线的位置关系是 .
25.如图,正方体ABCD﹣A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
①点E到平面ABC1D1的距离为;
②直线BC与平面ABC1D1所成角为45°;
③空间四边形ABCD1在正方体六个面内的射影围成的图形中,面积最小的值为;
④BE与CD1所成角的正弦值为;
⑤二面角A﹣BD1﹣C的大小为.
其中真命题是 .(写出所有真命题的序号)
26.在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为 .
三.解答题(共10小题)
27.已知:a?α,b?α,a∩b=A,P∈b,PQ∥a.求证:PQ?α.
28.正方体六个表面的中心所确定的直线中,异面直线共有多少对?
29.如图,在四棱锥p﹣ABCD中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,AB=1,AD=2,PA=CD=4.
(Ⅰ)求证:BD⊥PC;
(Ⅱ)求二面角B﹣PC﹣A的余弦值.
30.分别用文字语言、图形语言和符号语言书写面面平行的判定定理.
31.已知:四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且==,求证:直线FE、GH、AC交于一点.
32.三棱锥P﹣ABC中,PC=x,其余棱长均为1.
(1)求证:PC⊥AB;
(2)求三棱锥P﹣ABC的体积的最大值.
33.如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求异面直线AE与BC所成角的余弦值;
(Ⅲ)求AD与平面ABE所成角的正弦值.
34.已知E、F、G、H是所在线段上的点,且EH∥FG.
求证:EH∥BD.
35.如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=,E,F分别是BC,A1C的中点.
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, =λ.若CM∥平面AEF,求实数λ的值.
36.如图,在四棱台ABCD﹣A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.
(1)求证:BD⊥C1C;
(2)求证:C1C∥平面A1BD.
人教A版必修2《第2章 点、直线、平面之间的位置关系》2018年单元测试卷
参考答案与试题解析
一.选择题(共16小题)
1.若一个角的两边分别和另一个角的两边平行,那么这两个角( )
A.相等 B.互补 C.相等或互补 D.无法确定
【分析】本题应分两种情况讨论,如图,∠1,∠2,∠3的两边互相平行,由图形可以看出∠1和∠2是邻补角,它们和∠3的关系容易知道一个相等,一个互补.
【解答】解:如图,∠1,∠2,∠3的两边互相平行,
∴∠3=∠4,∠4=∠1,∠4+∠2=180°;
∴∠3=∠1,∠3+∠2=180°.
∴这两个角相等或互补.
故选:C.
【点评】解决本题时要联想的平行线的性质定理,正确认识其基本图形,就不会忽视互补的情况.熟记结论:如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补.
2.如图,各棱长均为1的正三棱柱ABC﹣A1B1C1,M,N分别为线段A1B,B1C上的动点,且MN∥平面ACC1A1,则这样的MN有( )
A.1条 B.2条 C.3条 D.无数条
【分析】任取线段A1B上一点M,过M作MH∥AA1,交AB于H,过H作HG∥AC交BC于G,过G作CC1的平行线,与CB1一定有交点N,且MN∥平面ACC1A1,则这样的MN有无数个.
【解答】解:如图,任取线段A1B上一点M,过M作MH∥AA1,交AB于H,过H作HG∥AC交BC于G,
过G作CC1的平行线,与CB1一定有交点N,且MN∥平面ACC1A1,则这样的MN有无数个.
故选:D.
【点评】不本题考查了空间线面位置关系,转化思想,属于中档题.
3.下列命题正确的个数是( )
①梯形的四个顶点在同一平面内
②三条平行直线必共面
③有三个公共点的两个平面必重合
④每两条相交的且交点各不相同的四条直线一定共面.
A.1个 B.2个 C.3个 D.4个
【分析】对四个命题一一判断,从而确定正确与否.
【解答】解:①梯形的四个顶点在同一平面内,正确;
②三条平行直线必共面不正确,如三棱柱的三条侧棱;
③有三个公共点的两个平面必重合不正确,若三个公共点共线;
④每两条相交的且交点各不相同的四条直线一定共面,正确.
故选:B.
【点评】本题考查了平面中的公理,属于基础题.
4.设a,b为两条直线,α,β为两个平面,下列四个命题中,正确的命题是( )
A.若a,b与α所成的角相等,则α∥b
B.若a∥α,b∥β,α∥β,则a∥b
C.若a?α,b?β,α∥b,则α∥β
D.若a⊥α,b⊥β,α⊥β,是a⊥b
【分析】根据题意,依次分析选项,A、用直线的位置关系判断.B、用长方体中的线线,线面,面面关系验证.C、用长方体中的线线,线面,面面关系验证.D、由a⊥α,α⊥β,可得到a?β或a∥β,再由b⊥β得到结论.
【解答】解:A、直线a,b的方向相同时才平行,不正确;
B、用长方体验证.如图,设A1B1为a,平面AC为α,BC为b,平面A1C1为β,显然有a∥α,b∥β,α∥β,但得不到a∥b,不正确;
C、可设A1B1为a,平面AB1为α,CD为b,平面AC为β,满足选项C的条件却得不到α∥β,不正确;
D、∵a⊥α,α⊥β,
∴a?β或a∥β
又∵b⊥β
∴a⊥b
故选:D.
【点评】本题主要考查空间内两直线,直线与平面,平面与平面间的位置关系,综合性强,方法灵活,属中档题.
5.已知AB∥PQ,BC∥QR,∠ABC=60°,则∠PQR等于( )
A.60° B.60°或120°
C.120° D.以上结论都不对
【分析】首先,直接根据平行关系求解即可.
【解答】解:∵AB∥PQ,BC∥QR,
且∠ABC=60°,
∴∠PQR=60°或120°
故选:B.
【点评】本题重点考查了平面的性质、平行关系运用.属于中档题.
6.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
A.在棱AD上存在点M,使AD⊥平面PMB
B.异面直线AD与PB所成的角为90°
C.二面角P﹣BC﹣A的大小为45°
D.BD⊥平面PAC
【分析】根据线面垂直,异面直线所成角的大小以及二面角的求解方法分别进行判断即可.
【解答】解:对于A,取AD的中点M,连PM,BM,则∵侧面PAD为正三角形,
∴PM⊥AD,
又底面ABCD是∠DAB=60°的菱形,
∴三角形ABD是等边三角形,
∴AD⊥BM,
∴AD⊥平面PBM,故A正确,
对于B,∵AD⊥平面PBM,
∴AD⊥PB,即异面直线AD与PB所成的角为90°,故B正确,
对于C,∵底面ABCD为菱形,∠DAB=60°平面PAD⊥平面ABCD,
∴BM⊥BC,则∠PBM是二面角P﹣BC﹣A的平面角,
设AB=1,则BM=,PM=,
在直角三角形PBM中,tan∠PBM=,
即∠PBM=45°,故二面角P﹣BC﹣A的大小为45°,故C正确,
故错误的是D,
故选:D.
【点评】本题主要考查空间直线和平面位置关系以及二面角的求解,根据相应的判断和证明方法是解决本题的关键.综合性较强,难度较大.
7.如图,在正方体ABCD﹣A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围是( )
A.[,] B.[0,1] C.[,] D.[,]
【分析】如图所示,作出平面MNQB1∥平面DEF,A1Q=2AQ,D1N=2ND,P的轨迹是线段QN,P在Q处,tan∠ABP=,P在N处,tan∠ABP==,即可得出结论.
【解答】解:如图所示,作出平面MNQB1∥平面DEF,则A1Q=2AQ,D1N=2ND,
∵PB1∥平面DEF,∴P的轨迹是线段QN.
P在Q处,tan∠ABP=,P在N处,tan∠ABP==,
故选:D.
【点评】本题考查线面、面面平行,考查线面角,考查学生分析解决问题的能力,属于中档题.
8.在正方体ABCD﹣A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,给出下列四个推断:
①FG∥平面AA1D1D; ②EF∥平面BC1D1;
③FG∥平面BC1D1; ④平面EFG∥平面BC1D1
其中推断正确的序号是( )
A.①③ B.①④ C.②③ D.②④
【分析】由FG∥BC1,BC1∥AD1,得FG∥AD1,从而FG∥平面BC1D1,FG∥平面AA1D1D;由EF∥A1C1,A1C1与平面BC1D1相交,从而EF与平面BC1D1相交,进而平面EFG与平面BC1D1相交.
【解答】解:∵在正方体ABCD﹣A1B1C1D1中,E,F,G分别是A1B1,B1C1,BB1的中点,
∴FG∥BC1,∵BC1∥AD1,∴FG∥AD1,
∵FG?平面AA1D1D,AD1?平面AA1D1D,∴FG∥平面AA1D1D,故①正确;
∵EF∥A1C1,A1C1与平面BC1D1相交,∴EF与平面BC1D1相交,故②错误;
∵E,F,G分别是A1B1,B1C1,BB1的中点,
∴FG∥BC1,∵FG?平面BC1D1,BC1?平面BC1D1,
∴FG∥平面BC1D1,故③正确;
∵EF与平面BC1D1相交,∴平面EFG与平面BC1D1相交,故④错误.
故选:A.
【点评】本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.
9.已知点P为△ABC所在平面外一点,点D、E、F分别在直线PA、PB、PC上,平面DEF∥平面ABC,且===,则=( )
A. B. C. D.
【分析】根据题意得到△DEF∽△ABC,则相似三角形的面积之比等于相似比的平方.
【解答】解:如图,∵平面DEF∥平面ABC,
∴△DEF∽△ABC,DE∥AB,EF∥BC,DF∥AC,
∴=.
又===,
∴=,
∴==,
∴=()2=.
故选:B.
【点评】本题考查了平面与平面平行的性质:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
10.在底面是菱形的四棱锥P﹣ABCD中,PA⊥底面ABCD,点E为棱PB的中点,点F在棱AD上,平面CEF与PA交于点K,且PA=AB=3,AF=2,则等于( )
A. B. C. D.
【分析】如图所示,延长BA,CF,交于G,连接EG,与PA交于K,则AG=6,过A做AH∥PB,与EG交于H,则==,即可得出结论.
【解答】解:如图所示,延长BA,CF,交于G,连接EG,与PA交于K,则AG=6,
过A做AH∥PB,与EG交于H,则====,
故选:A.
【点评】本题考查棱锥的结构特征,考查平面与平面交线的求法,属于中档题.
11.已知平面α,β所成的二面角为80°,P为α,β外一定点,则过点P作直线与α,β都成30°的直线有( )
A.1条 B.2条 C.3条 D.4条
【分析】过P作平面A垂直于α、β的交线l,并且交l于点0,连接PO,则PO垂直于l,过点P在A内做OP的垂线L',以PO为轴在垂直于PO的平面内转动L',根据三垂线定理可得有两条直线满足题意.以P点为轴在平面A内前后转动L',根据三垂线定理可得也有两条直线满足题意.
【解答】解:首先给出下面两个结论
①两条平行线与同一个平面所成的角相等.
②与二面角的两个面成等角的直线在二面角的平分面上.
图1.
(1)如图1,过二面角α﹣l﹣β内任一点作棱l的垂面AOB,交棱于点O,与两半平面于OA,OB,则∠AOB为二面角α﹣l﹣β的平面角,∠AOB=80°
设OP1为∠AOB的平分线,则∠P1OA=∠P1OB=40°,与平面α,β所成的角都是30°,此时过P且与OP1平行的直线符合要求,当OP1以O为轴心,在二面角α﹣l﹣β的平分面上转动时,OP1与两平面夹角变小,会对称的出现两条符合要求成30°情形.
图2.
(2)如图2,设OP2为∠AOB的补角∠AOB′的平分线,则∠P2OA=∠P2OB=50°,与平面α,β所成的角都是50°.当OP2以O为轴心,在二面角α﹣l﹣β′的平分面上转动时,
OP2与两平面夹角变小,对称地在图中OP2两侧会出现30°情形,有两条.此时过P且与OP2平行的直线符合要求,有两条.
综上所述,直线的条数共有4条.
故选:D.
【点评】本题主要考查线面角,以及考查解决线面角的特殊方法的应用,考查空间想象能力,体现了转化的思想和运动变化的思想方法,此题是个难题.
12.如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( )
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积
【分析】A.由于平面QEF即为对角面A1B1CD,点P为A1D1的中点,可得:点P到平面QEF即到对角面A1B1CD的距离=为定值;
D.由于点Q到直线CD的距离是定值a,|EF|为定值,因此△QEF的面积=为定值;
C.由A.D可知:三棱锥P﹣QEF的体积为定值;
B.用排除法即可得出.
【解答】解:A.∵平面QEF即为对角面A1B1CD,点P为A1D1的中点,∴点P到平面QEF即到对角面A1B1CD的距离=为定值;
D.∵点Q到直线CD的距离是定值a,|EF|为定值,∴△QEF的面积=为定值;
C.由A.D可知:三棱锥P﹣QEF的体积为定值;
B.直线PQ与平面PEF所成的角与点Q的位置有关系,因此不是定值,或用排除法即可得出.
综上可得:只有B中的值不是定值.
故选:B.
【点评】本题综合考查了正方体的性质、三棱锥的体积、点到平面的距离、异面直线所成的角等基础知识与基本技能方法,考查了推理能力和空间想象能力,属于难题.
13.已知m,n是两条不重合的直线,α,β是不重合的平面,下面四个命题中正确的是( )
A.若m?α,n?β,m⊥n,则α⊥β B.若m∥α,m⊥n,则n⊥α
C.若m⊥α,m⊥β,则α∥β D.若m⊥n,m⊥β,则n∥β
【分析】在A中,α与β相交或平行;在B中,n与α相交、平行或n?α;在C中,由面面平行的判定定理得α∥β;在D中,n∥β或n?β.
【解答】解:由m,n是两条不重合的直线,α,β是不重合的平面,知:
在A中:若m?α,n?β,m⊥n,则α与β相交或平行,故A错误;
在B中:若m∥α,m⊥n,则n与α相交、平行或n?α,故B错误;
在C中:若m⊥α,m⊥β,则由面面平行的判定定理得α∥β,故C正确;
在D中:若m⊥n,m⊥β,则n∥β或n?β,故D错误.
故选:C.
【点评】本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.
14.如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为( )
A.直线BE与直线CF共面
B.直线BE与直线AF是异面直线
C.平面BCE⊥平面PAD
D.面PAD与面PBC的交线与BC平行
【分析】几何体的展开图,复原出几何体,利用异面直线的定义判断A,B的正误;
利用直线与平面垂直的判定定理判断C的正误;利用直线与平面平行的判定、性质定理判断D的正误.
【解答】解:画出几何体的图形,如图,
由题意可知,A,直线BE与直线CF共面,正确,
因为E,F是PA与PD的中点,可知EF∥AD,
所以EF∥BC,直线BE与直线CF是共面直线;
B,直线BE与直线AF异面;满足异面直线的定义,正确.
C,因为△PAB是等腰三角形,BE与PA的关系不能确定,所以平面BCE⊥平面PAD,不正确.
D,∵AD∥BC,∴AD∥平面PBC,∴面PAD与面PBC的交线与BC平行,正确.
故选:C.
【点评】本题是中档题,考查空间图形中直线与直线、平面的位置关系,考查异面直线的判断,基本知识与定理的灵活运用.
15.如图,△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,此图中直角三角形的个数为( )
A.1 B.2 C.3 D.4
【分析】推导出AB⊥BC,PA⊥BC,从而BC⊥平面PAB,由此能求出图中直角三角形的个数.
【解答】解:∵△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,
∴AB⊥BC,PA⊥BC,
∵AB∩PA=A,∴BC⊥平面PAB,
∴图中直角三角形有△ABC(∠ABC是直角 ),
△PAC(∠PAC是直角),△PAB(∠PAB是直角),△PBC(∠PBC是直角),
∴图中直角三角形有4个.
故选:D.
【点评】本题考查几何体中直角三角形的个数的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、考查函数与方程思想、数形结合思想,是基础题.
16.过三棱柱任意两个顶点作直线,在所有这些直线中任取其中两条,则它们成为异面直线的概率是( )
A. B. C. D.
【分析】先求出总共可以做多少直线,然后通过分类找出能成为异面直线的数量,最后二者相比求概率即可
【解答】解:从三棱柱的六个顶点中任取两点作直线,可做直线条
从这15条直线中任取两条,共种
其中成异面直线可分为以下几类:
(1)侧棱与底面边:有3×2=6对
(2)侧棱与侧面对角线:有3×2=6对
(3)底面边与侧面对角线:有3×2+3×2=6+6=12对
(4)底面边与底面边:有3×2=6对
(5)侧面对角线与侧面对角线:对
共6+6+12+6+6=36对
∴两直线为异面直线的概率为:
故选:D.
【点评】本题考查异面直线的判定和等可能事件的概率,要求弄精确分类.分类较容易出错,每一类中比较容易重复或遗漏.要有较强的空间想象力和观察力.属较难题
二.填空题(共10小题)
17.空间中一个角∠A的两边和另一个角∠B的两边分别平行,∠A=70°,则∠B= 70°或110° .
【分析】由空间两条平行线的性质和等角定理,可得∠B与∠A相等或∠B与∠A互补,由此不难得到正确答案.
【解答】解:①若角∠A的两边和角∠B的两边分别平行,且方向相同,则∠A与∠B相等
此时∠B=∠A=70°;
②当角∠A的两边和角∠B的两边分别平行,且一边方向相同另一边方向相反,则∠A与∠B互补,
此时∠B=180°﹣∠A=110°.
故答案为:70°或110°
【点评】本题给出空间一个角的两边分别与另一个角的两边平行,求它们之间的度数关系,考查了空间两条平行线的性质和等角定理等知识,属于基础题.
18.下列各图是正方体和正三棱柱(两底面为正三角形的直棱柱),G、N、M、H分别是顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有 ③ .
【分析】根据已知中的图形,结合棱柱的几何特征及异面直线的判定定理,逐一分析直线GH、MN的位置关系,可得答案.
【解答】解:①中GH∥MN,GH=MN,故不满足条件;
②中G、N、M、H四点在如图所示的平面中,
故不满足条件;
③中,GH?左侧面,MN∩左侧面=N,N?GH,
故直线GH、MN是异面直线,
④中,GH∥MN,故不满足条件,
故答案为:③.
【点评】本题考查的知识点是棱柱的几何特征及异面直线的判定定理,难度中档.
19.已知l,m为直线,α为平面,l∥α,m?α,则l与m之间的关系是 平行或异面 .
【分析】以正方体为载体,列举出所有情况,能求出两直线间的关系.
【解答】解:在正方体ABCD﹣A1B1C1D1中,
A1B1∥平面ABCD,AB?平面ABCD,BC?平面ABCD,
A1B1与AB平行,A1B1与BC异面,
∴l,m为直线,α为平面,l∥α,m?α,
则l与m之间的关系是平行或异面.
故答案为:平行或异面.
【点评】本题考查两直线间的位置关系的判断,考查空间中空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想,属于中档题.
20.设α和β为不重合的两个平面,给出下列命题:
(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;
(2)若α外一条直线l与α内的一条直线平行,则l和α平行;
(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;
(4)如果l与α内的两条直线垂直则直线l与α垂直.
上面命题中,真命题的序号 ①② (写出所有真命题的序号).
【分析】在①中,由面面平行的判定定理得α平行于β;在②中,由线面平行的判定定理得l和α平行;在③中,α与β所成的角可能是锐角,也可能是直角,也可能是钝角;在④中,只有l与α内的两条相交直线垂直,才有直线与α垂直.
【解答】解:由设α,β为不重合的两个平面,知:
在①中,若α内的两条相交直线分别平行于β内的两条直线,则由面面平行的判定定理得α平行于β,故①正确;
在②中,若α外一条直线l与α内的一条直线平行,则由线面平行的判定定理得l和α平行,故②正确;
在③中,设α和β相交于直线l,若α内有一条直线垂直于l,则α与β所成的角可能是锐角,也可能是直角,也可能是钝角,故③错误;
在④中,只有l与α内的两条相交直线垂直,才有直线与α垂直,故④错误.
故答案为:①②.
【点评】本题考查命题真假的判断,考查空间中线线、线面、面面的位置关系等基础知识,考查学生分析解决问题的能力,是中档题.
21.如图,在正三棱柱A1B1C1﹣ABC中,AB=2,A1A=2,D,F分别是棱AB,AA1的中点,E为棱AC上的动点,则△DEF周长的最小值为 +2 .
【分析】由正三棱柱A1B1C1﹣ABC的性质可得:AA1⊥AB,AA1⊥AC.在Rt△ADF中,利用勾股定理可得DF=2.因此只要求出DE+EF的最小值即可得出.把底面ABC展开与侧面ACC1A1在同一个平面,如图所示,只有当三点D,E,F在同一条直线时,DE+EF取得最小值.利用余弦定理即可得出.
【解答】解:由正三棱柱A1B1C1﹣ABC,可得AA1⊥底面ABC,∴AA1⊥AB,AA1⊥AC.
在Rt△ADF中,DF==2.
把底面ABC展开与侧面ACC1A1在同一个平面,如图所示,
只有当三点D,E,F在同一条直线时,DE+EF取得最小值.
在△ADE中,∠DAE=60°+90°=150°,由余弦定理可得:
DE==.
∴△DEF周长的最小值=+2.
故答案为: +2.
【点评】本题考查了空间几何位置关系、余弦定理、侧面展开图,考查了转化能力、数形结合能力、推理能力与计算能力,属于难题.
22.已知a,b是一对异面直线,且a,b成70°角.P为空间一定点,则在过P点的直线中与a,b所成角都为70°的直线有 4 条.
【分析】如图所示,α∥β,a?α,b?β.任取P∈B,过点P作a′∥a,则a′?β.过点P可作PA满足与直线a′,b所成角都为70°的直线,其中PA在∠MPN的上方.同理可以作出其它3条,当点P不在其中一条直线上时,可以通过平移两条异面直线即可.
【解答】解:如图所示,
α∥β,a?α,b?β.
?P∈β,过点P作a′∥a,则a′?β.
过点P可作PA满足与直线a′,b所成角都为70°的直线,其中PA在∠MPN的上方.
同理可以作出其它3条,PB,PC,PD(∵70°+70°>110°).
当点P不在其中一条直线上时,可以通过平移两条异面直线即可.
综上可得:在过P点的直线中与a,b所成角都为70°的直线有4条.
故答案为:4.
【点评】本题考查了异面直线所成的夹角、平移变换、分类讨论方法等基础知识与基本技能方法,考查了推理能力和空间想象能力,属于难题.
23.“直线l与平面α相交于点P”用集合语言表示为 l∩α=P .
【分析】利用空间线面关系对应的符号语言表示出来.
【解答】解:直线l与平面α相交于点P,用集合语言表示为l∩α=P;
故答案为:l∩α=P.
【点评】本题考查了平面与直线位置关系的集合表示;属于基础题.
24.在空间平行于同一直线的两条直线的位置关系是 平行 .
【分析】根据平行公理可以证明.
【解答】解:根据平行公理可知:在空间平行于同一直线的两条直线的位置关系是平行的.
故答案为:平行.
【点评】本题主要考查空间直线的位置关系的判断,利用平行公理是解决本题的关键,比较基础.
25.如图,正方体ABCD﹣A1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:
①点E到平面ABC1D1的距离为;
②直线BC与平面ABC1D1所成角为45°;
③空间四边形ABCD1在正方体六个面内的射影围成的图形中,面积最小的值为;
④BE与CD1所成角的正弦值为;
⑤二面角A﹣BD1﹣C的大小为.
其中真命题是 ②③④ .(写出所有真命题的序号)
【分析】对5个命题分别进行判断,即可得出结论.
【解答】解:①由于A1B1∥平面ABC1D1,故B1到平面ABC1D1的距离即点E到平面ABC1D1的距离,
连接B1C交BC1于F,则易得B1F垂直于平面ABC1D1,而B1F=,故点E到平面ABC1D1的距离为,故①错;
②易得B1C垂直于平面ABC1D1,故∠CBC1为直线BC与平面ABC1D1所成的角,且为45°,故②正确;
③易得空间四边形ABCD1在正方体的面ABCD、面A1B1C1D1内的射影面积为1,在面BB1C1C内、面AA1D1D内的射影面积为,在面ABB1A1内、面CC1D1D内的射影面积为,故③正确;
④BE与CD1所成的角,即为BA1与BE所成角,即为∠A1BE,A1E=,BE=,BA1=,cos∠A1BE==,sin∠A1BE=,故④正确;
⑤在直角三角形BAD1中过A作AH垂直于BD1,连接CH,易知CH垂直于BD1,故∠AHC是二面角A﹣BD1﹣C的平面角,由余弦定理得,cos∠AHC==﹣,故∠AHC=,故⑤错.
故答案为:②③④
【点评】本题考查命题的真假判断,考查空间线面位置关系,考查空间角,考查学生分析解决问题的能力,知识综合性强.
26.在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为 [10°,50°] .
【分析】平移CB1到A处,由已知得∠B1CA=30°,∠B1AC=150°,0≤∠C1AC≤20°,由此能求出直线B1C与直线AC1所成角的取值范围.
【解答】解:∵在△ABC中,∠BAC=10°,∠ACB=30°,
将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,
如图,平移CB1到A处,B1C绕AC旋转,
∴∠B1CA=30°,∠B1AC=150°,
AC1绕AB旋转,∴0°≤∠C1AC≤2∠CAB,
∴0≤∠C1AC≤20°,
设直线B1C与直线AC1所成角为α,
则∠B1AC﹣∠C1AC≤α≤∠B1AC+∠C1AC,
∵130°≤∠B1AC﹣∠C1AC≤150°,
150°≤∠B1AC+∠C1AC≤170°,
∴10°≤α≤50°或130°≤α≤170°(舍).
故答案为:[10°,50°].
【点评】本题考查两直线所成角的取值的求法,解题时要认真审题,注意旋转性质的合理运用,是难题.
三.解答题(共10小题)
27.已知:a?α,b?α,a∩b=A,P∈b,PQ∥a.求证:PQ?α.
【分析】首先根据两条直线平行,得到一个确定的平面,根据直线a?β,点P∈β,p∈b,b?α,确定p∈α,根据一条直线和直线外一点可以确定一个平面,得到另个平面是同一个平面,得到结论.
【解答】证明∵PQ∥a,
∴PQ与a确定一个平面β,
∴直线a?β,点P∈β.
∵p∈b,b?α,
∴p∈α
∵a?α,
∴α与β重合,
∴PQ?α
【点评】本题主要考查用平面公理和推论证明共面问题的方法,考查两条平行线确定一个平面,考查两条相交线确定一个平面,考查用同一法证明两个平面重合,实际上这种利用公理证明问题的题目,比较抽象.
28.正方体六个表面的中心所确定的直线中,异面直线共有多少对?
【分析】根据图形结构的对称性,先求出对每一条边,与其异面的边有4个,共有多不对异面直线,再求出每一条边与相对顶点连线中的1条异面,共有多少对异面直线,由此能求出结果.
【解答】解:根据图形结构的对称性,
对每一条边,与其异面的边有4个,共=24对异面直线,
每一条边与相对顶点连线中的1条异面,共有12对异面直线,
综上,正方体六个表面的中心所确定的直线中,异面直线共有36对.
【点评】本题考查满足条件的异面直线有多少对的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.
29.如图,在四棱锥p﹣ABCD中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,AB=1,AD=2,PA=CD=4.
(Ⅰ)求证:BD⊥PC;
(Ⅱ)求二面角B﹣PC﹣A的余弦值.
【分析】(1)以A为原点,建立如图所示空间直角坐标系,求出与的坐标,利用它们的数量积为零证得BD⊥OC;
(2)易证为面PAC的法向量,求出面PBC的法向量,然后求出两法向量的夹角,利用两平面的法向量的夹角与二面角的平面角相等或互补,即可求得二面角B﹣PC﹣A的余弦值.
【解答】证明:(Ⅰ)以A为原点,建立如图所示空间直角坐标系,
则B(0,1,0),C(﹣2,4,0),D(﹣2,0,0),P(0,0,4),
∴,,
∴
所以PC⊥BD.
(Ⅱ)易证为面PAC的法向量,
设面PBC的法向量n=(a,b,c),
所以?
所以面PBC的法向量n=(6,4,1),
∴cosθ=﹣.
因为面PAC和面PBC所成的角为锐角,
所以二面角B﹣PC﹣A的余弦值为.
【点评】本题主要考查了平面与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.
30.分别用文字语言、图形语言和符号语言书写面面平行的判定定理.
【分析】面面平行判定定理的内容用文字叙述、图形语言以及几何符号表示,分别写出即可.
【解答】解:面面平行的判定定理;
(1)文字语言是“如果两个一个平面内有两个相交直线与另一个平面平行,则这两个平面平行”;
(2)图形语言表示:如图所示:
(3)用符号语言表示: ?α∥β.
【点评】本题考查了平面与平面平行的判定定理,熟练掌握平面平行的判定定理是解答本题的关键,是基础题.
31.已知:四边形ABCD是空间四边形,E,H分别是边AB,AD的中点,F,G分别是边CB,CD上的点,且==,求证:直线FE、GH、AC交于一点.
【分析】证明四边形EFGH是梯形,得出EF,HG相交于一点,再利用面面相交即可证明直线FE、GH、AC交于一点.
【解答】证明:连接BD,∵E,H分别是边AB,AD的中点,
∴EH∥BD;…(2分)
又∵==,∴FG∥BD;…(4分)
因此EH∥FG且EH≠FG;…(6分)
故四边形EFGH是梯形;
所以EF,HG相交,设EF∩HG=K,…(8分)
∵K∈EF,EF?平面ABC,
∴K∈平面ABC;
同理K∈平面ACD,…(10分)
又平面ABC∩平面ACD=AC,∴K∈AC,
故直线FE、GH、AC交于一点.…(12分)
【点评】本题考查了证明三线相交的应用问题,通常是先证明两线交于一点,再证第三条直线过交点即可.
32.三棱锥P﹣ABC中,PC=x,其余棱长均为1.
(1)求证:PC⊥AB;
(2)求三棱锥P﹣ABC的体积的最大值.
【分析】(1)取AB中点M,由△PAB与△CAB均为正三角形,知AB⊥PM,AB⊥CM,由此能够证明AB⊥PC.
(2)当PM⊥平面ABC时,三棱锥的高为PM,由此能求出三棱锥P﹣ABC的体积的最大值.
【解答】解:(1)取AB中点M,
∵△PAB与△CAB均为正三角形,
∴AB⊥PM,AB⊥CM,
∴AB⊥平面PCM,
∴AB⊥PC.
(2)当PM⊥平面ABC时,
三棱锥的高为PM,
此时.
【点评】本题考查PC⊥AB的证明和求三棱锥P﹣ABC的体积的最大值.解题时要认真审题,仔细解答,注意合理地进行等价转化.
33.如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求异面直线AE与BC所成角的余弦值;
(Ⅲ)求AD与平面ABE所成角的正弦值.
【分析】(Ⅰ)先利用P、Q分别是AE、AB的中点?PQ∥BE,PQ=,再利用DC∥BE,DC=可以推出PQ∥DC进而证明PQ∥平面ACD;
(Ⅱ)取BE的中点F,可以先推出QF∥AE且QF=AE,所以∠DFQ就是异面直线AE与BC所成的角,然后在△DFQ中求出
∠DFQ的余弦值即可.
(Ⅲ)由AC=BC和Q为AB的中点可得CQ⊥AB,再利用DC⊥平面ABC,可得CQ⊥平面ABE,进而推出DP⊥平面ABE,所以∠DAP就是AD与平面ABE所成的角,在△DAP中求出∠DAP即可.
【解答】解:(Ⅰ)证明:由已知:P、Q分别是AE、AB的中点,
所以,PQ∥BE,PQ=BE,
又DC∥BE,DC=BE
所以,PQ∥DC
所以,PQ∥平面ACD(4分)
(Ⅱ)取BE的中点F,连接QF,DF,DQ,可以推出QF∥AE且QF=AE,
易证∠DFQ就是异面直线AE与BC所成的角
易知CQ=1,AB=2,AE=4,QF=2,DF=BC=2,DQ=
由余弦定理:可得cos∠DFQ=(8分)
(Ⅲ)由AC=BC和Q为AB的中点可得CQ⊥AB,
再利用DC⊥平面ABC,可得CQ⊥平面ABE,进而推出DP⊥平面ABE
所以∠DAP就是AD与平面ABE所成的角
DP=CQ=1,AD=
所以AD与平面ABE所成角的正弦值为.(12分)
【点评】本题涉及了线面平行以及线线所成角和线面所成角,是对立体几何知识的综合考查.在证明线面平行时,其常用方法是在平面内找已知直线平行的直线.当然也可以用面面平行来推导线面平行.
34.已知E、F、G、H是所在线段上的点,且EH∥FG.
求证:EH∥BD.
【分析】根据一条直线在平面上,一条直线与这条直线平行,根据这两个条件得到直线与平面平行,根据线与面平行的性质,得到线与线平行,得到结论.
【解答】证明:∵点E、F、G、H为空间四边形边AB、BC、CD、DA上的点
∴直线EH?平面BCD,直线FG?平面BCD
又EH∥FG
∴直线EH∥平面BCD
又∵EH?平面ABD且平面ABD∩平面BCD=BD
∴EH∥BD
【点评】本题考查线与面平行的判断,线与面平行的性质,考查线面平行的判定和性质的综合应用,本题是一个考查知识点比较集中的题目,只考线与面的平行,是一个目标很明确的题目.
35.如图,在直四棱柱ABCD﹣A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=,E,F分别是BC,A1C的中点.
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, =λ.若CM∥平面AEF,求实数λ的值.
【分析】(1)建立坐标系,求出直线的向量坐标,利用夹角公式求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, =λ.求出平面AEF的法向量,利用CM∥平面AEF,即可求实数λ的值.
【解答】解:因为四棱柱ABCD﹣A1B1C1D1为直四棱柱,
所以A1A⊥平面ABCD.
又AE?平面ABCD,AD?平面ABCD,
所以A1A⊥AE,A1A⊥AD.
在菱形ABCD中∠ABC=,则△ABC是等边三角形.
因为E是BC中点,所以BC⊥AE.
因为BC∥AD,所以AE⊥AD.
建立空间直角坐标系.则A(0,0,0),C(,1,0),D(0,2,0),
A1(0,0,2),E(,0,0),F(,,1).
(1)=(0,2,0),=(﹣,,1),
所以异面直线EF,AD所成角的余弦值为=. …(4分)
(2)设M(x,y,z),由于点M在线段A1D上,且=λ,
则(x,y,z﹣2)=λ(0,2,﹣2).
则M(0,2λ,2﹣2λ),=(﹣,2λ﹣1,2﹣2λ). …(6分)
设平面AEF的法向量为=(x0,y0,z0).
因为=(,0,0),=(,,1),
由,得x0=0, y0+z0=0.
取y0=2,则z0=﹣1,
则平面AEF的一个法向量为n=(0,2,﹣1). …(8分)
由于CM∥平面AEF,则=0,即2(2λ﹣1)﹣(2﹣2λ)=0,解得λ=.…(10分)
【点评】本题考查线面角,考查线面平行的运用,考查向量知识的运用,属于中档题.
36.如图,在四棱台ABCD﹣A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.
(1)求证:BD⊥C1C;
(2)求证:C1C∥平面A1BD.
【分析】(1)由AA1⊥平面ABCD,可证AA1⊥BD.四边形ABCD是菱形可得AC⊥BD,由线面垂直的判定定理可证BD⊥面ACC1A1,再由线面垂直的性质定理可证BD⊥CC1.
(2)连接AC和A1C1,设AC∩BD=E,先证明四边形ECC1A1为平行四边形,可得CC1∥A1E,再由线面平行的判定定理可证CC1∥平面A1BD.
【解答】证明:(1)∵AA1⊥平面ABCD,
∴AA1⊥BD.
∵四边形ABCD是菱形,∴AC⊥BD,
又 AC∩AA1=A,∴BD⊥面ACC1A1.
由CC1?面ACC1A1,
∴BD⊥CC1.
(2)连接AC和A1C1,设 AC∩BD=E,由于底面ABCD是平行四边形,故E为平行四边形ABCD的
中心,由棱台的定义及AB=2AD=2A1B1,可得 EC∥A1C1,且 EC=A1C1,
故ECC1A1为平行四边形,∴CC1∥A1E,而CC1?平面A1BD,A1E?平面A1BD,
∴CC1∥平面A1BD.
【点评】本题考查线面平行、垂直的判定定理、线面平行、垂直的性质定理的应用,体现了数形结合的数学思想,属于中档题.
