4.2.1 立体图形的三视图同步练习
图片预览

文档简介
第四章 投影与视图
2 视图
第1课时 立体图形的三视图
课前预习
1.三视图的意义
通常我们把从正面得到的视图叫做______________,从左面得到的视图叫做____________,从上面得到的视图叫做________________。
2.三种视图的画法
(1)位置:先画________,然后在主视图的下面画出__________,在主视图的右面画出_____________。
(2)大小:主、俯视图要_____________,主、左视图要_____________,左、俯视图要_____________。
(3)在画三视图时,看得见部分的轮廓线要画成______线,看不见部分的轮廓线要画成_____线。
课内探究
探究要点1 物体的三种视图
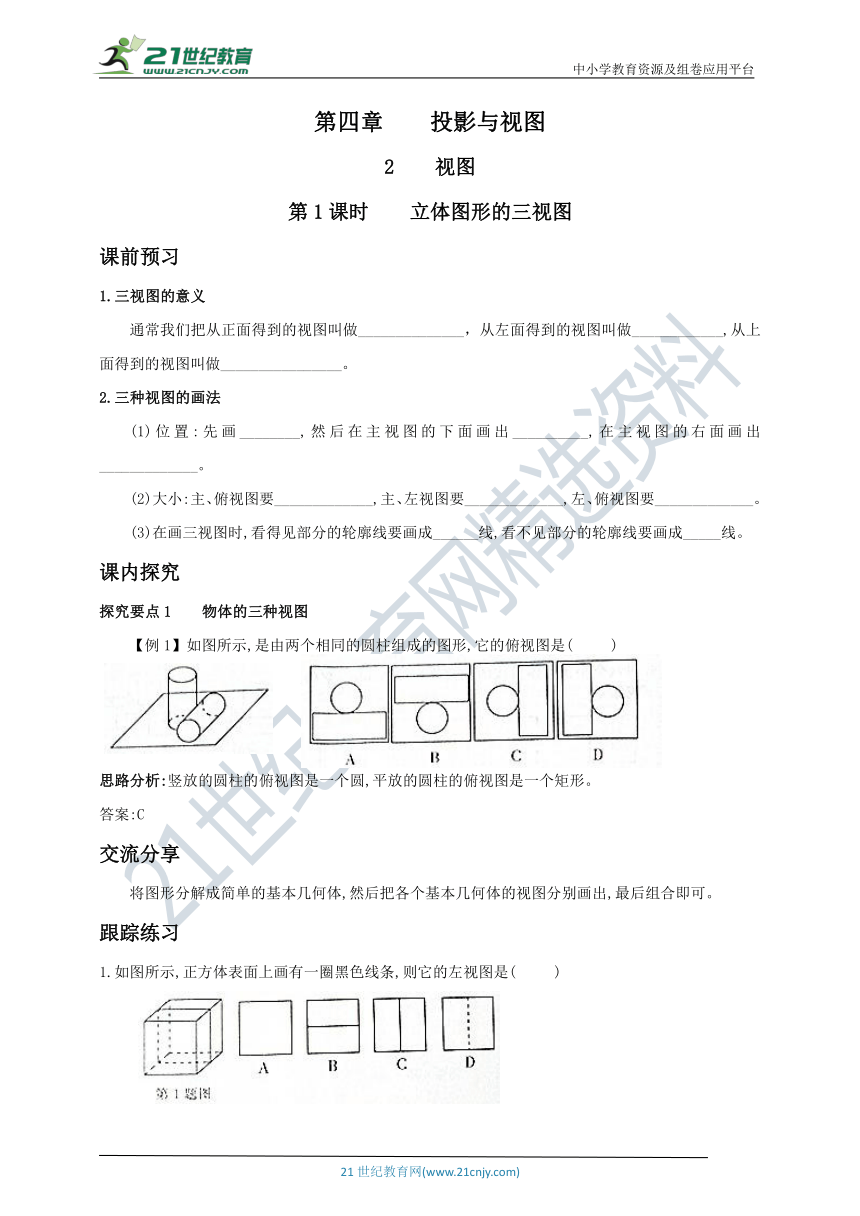
【例1】如图所示,是由两个相同的圆柱组成的图形,它的俯视图是( )
思路分析:竖放的圆柱的俯视图是一个圆,平放的圆柱的俯视图是一个矩形。
答案:C
交流分享
将图形分解成简单的基本几何体,然后把各个基本几何体的视图分别画出,最后组合即可。
跟踪练习
1.如图所示,正方体表面上画有一圈黑色线条,则它的左视图是( )
交探究要点2 画物体的三种视图
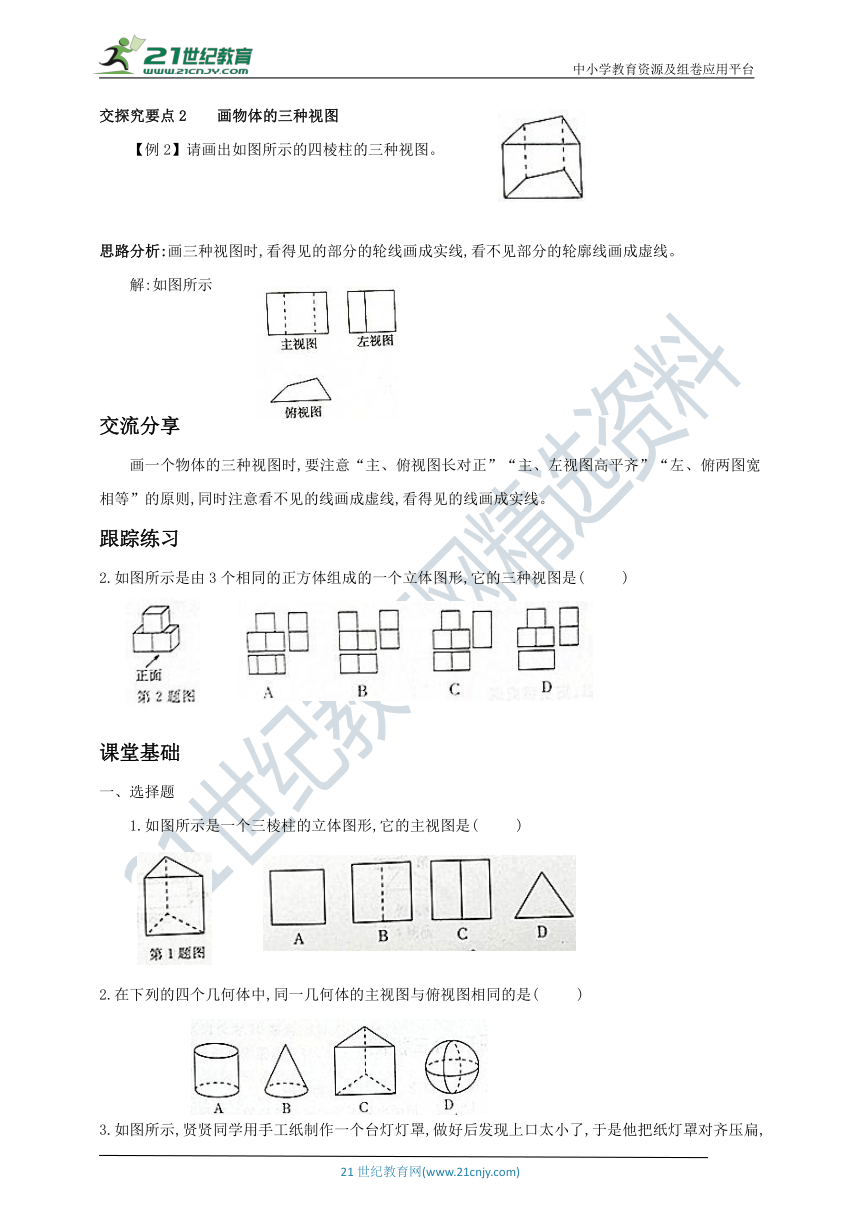
【例2】请画出如图所示的四棱柱的三种视图。
思路分析:画三种视图时,看得见的部分的轮线画成实线,看不见部分的轮廓线画成虚线。
解:如图所示
交流分享
画一个物体的三种视图时,要注意“主、俯视图长对正”“主、左视图高平齐”“左、俯两图宽相等”的原则,同时注意看不见的线画成虚线,看得见的线画成实线。
跟踪练习
2.如图所示是由3个相同的正方体组成的一个立体图形,它的三种视图是( )
课堂基础
一、选择题
1.如图所示是一个三棱柱的立体图形,它的主视图是( )
2.在下列的四个几何体中,同一几何体的主视图与俯视图相同的是( )
3.如图所示,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是( )
4.如图所示,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是_____________。
三、解答题
5.画出如图所示立体图形的三视图。
四、拓展探究题
6.如图所示,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图②所示,左视图中包含两个全等的矩形,如果用彩色胶带(如图①所示)包扎礼盒,求所需胶带的长度.(保留两位小数)
课后提升
1.如图所示的几何体的俯视图是( )
2.如图所示,该几何体的主视图是( )
3.如图所示,将一个圆柱放置在长方体上,其中圆柱的底面直径与长方体的宽相等,则该几何体的左视图是( )
4.由六个小正方体搭成的几何体如图所示,则它的主视图是( )
5.画出如图所示几何体的三视图。
5.个棱长为1的正方体组成如图所示的几何体。
(1)该几何体的体积是___________,表面积是__________。
(2)画出该几何体的主视图和左视图。
参考答案及解析
课前预习
1.主视图 左视图 俯视图
2.(1)主视图 俯视图 左视图 (2)长对正 高平齐 宽相等 (3)实 虚
课内探究
跟踪练习 1.C 2.A
课堂基础 1.B 2.D 3.B 4.3
5.解:如图所示
6.解:根据题意,作出实际图形的上底,如图所示,AC,CD是上底面的两边。
则AC=60÷2=30(cm),∠ACD=120°。作CB⊥AD于点B
那么AB=AC×sin60°=15(cm), 所以AD=2AB=30(cm),
胶带的长至少=30×6+20×6≈431.77(cm)
课后提升
1.B 解析:从上面看左边一个正方形,右边一个正方形,故选B.
2.B 3.A 4.B
5.解:如图所示:
(2)如图所示。
2 视图
第1课时 立体图形的三视图
课前预习
1.三视图的意义
通常我们把从正面得到的视图叫做______________,从左面得到的视图叫做____________,从上面得到的视图叫做________________。
2.三种视图的画法
(1)位置:先画________,然后在主视图的下面画出__________,在主视图的右面画出_____________。
(2)大小:主、俯视图要_____________,主、左视图要_____________,左、俯视图要_____________。
(3)在画三视图时,看得见部分的轮廓线要画成______线,看不见部分的轮廓线要画成_____线。
课内探究
探究要点1 物体的三种视图
【例1】如图所示,是由两个相同的圆柱组成的图形,它的俯视图是( )
思路分析:竖放的圆柱的俯视图是一个圆,平放的圆柱的俯视图是一个矩形。
答案:C
交流分享
将图形分解成简单的基本几何体,然后把各个基本几何体的视图分别画出,最后组合即可。
跟踪练习
1.如图所示,正方体表面上画有一圈黑色线条,则它的左视图是( )
交探究要点2 画物体的三种视图
【例2】请画出如图所示的四棱柱的三种视图。
思路分析:画三种视图时,看得见的部分的轮线画成实线,看不见部分的轮廓线画成虚线。
解:如图所示
交流分享
画一个物体的三种视图时,要注意“主、俯视图长对正”“主、左视图高平齐”“左、俯两图宽相等”的原则,同时注意看不见的线画成虚线,看得见的线画成实线。
跟踪练习
2.如图所示是由3个相同的正方体组成的一个立体图形,它的三种视图是( )
课堂基础
一、选择题
1.如图所示是一个三棱柱的立体图形,它的主视图是( )
2.在下列的四个几何体中,同一几何体的主视图与俯视图相同的是( )
3.如图所示,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是( )
4.如图所示,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是_____________。
三、解答题
5.画出如图所示立体图形的三视图。
四、拓展探究题
6.如图所示,上、下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图②所示,左视图中包含两个全等的矩形,如果用彩色胶带(如图①所示)包扎礼盒,求所需胶带的长度.(保留两位小数)
课后提升
1.如图所示的几何体的俯视图是( )
2.如图所示,该几何体的主视图是( )
3.如图所示,将一个圆柱放置在长方体上,其中圆柱的底面直径与长方体的宽相等,则该几何体的左视图是( )
4.由六个小正方体搭成的几何体如图所示,则它的主视图是( )
5.画出如图所示几何体的三视图。
5.个棱长为1的正方体组成如图所示的几何体。
(1)该几何体的体积是___________,表面积是__________。
(2)画出该几何体的主视图和左视图。
参考答案及解析
课前预习
1.主视图 左视图 俯视图
2.(1)主视图 俯视图 左视图 (2)长对正 高平齐 宽相等 (3)实 虚
课内探究
跟踪练习 1.C 2.A
课堂基础 1.B 2.D 3.B 4.3
5.解:如图所示
6.解:根据题意,作出实际图形的上底,如图所示,AC,CD是上底面的两边。
则AC=60÷2=30(cm),∠ACD=120°。作CB⊥AD于点B
那么AB=AC×sin60°=15(cm), 所以AD=2AB=30(cm),
胶带的长至少=30×6+20×6≈431.77(cm)
课后提升
1.B 解析:从上面看左边一个正方形,右边一个正方形,故选B.
2.B 3.A 4.B
5.解:如图所示:
(2)如图所示。
