4.2.2 由三视图还原几何体同步练习
图片预览

文档简介
第四章 投影与视图
2 视图
第2课时 由三视图还原几何体
课前预习
由三视图还原几何体
(1)在三种视图中____________反映物体的长和高,___________反映物体的长和宽,________反映物体的高和宽。
(2)由三视图复原儿何体,要先分别根据_____________、___________和___________想象立体图形的前面、左侧面和上面,然后再综合在一起想象整体图形。
课内探究
探究要点 由物体的三视图画立体图形
【例】如图所示,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块以搭成一个大正方体,至少还需要_______个小立方块。
思路分析:由三视图易得最底层有7个小立方第二层有2个小立方体,第三层有1个小立方体那么共有7+2-1=10个小立方体,若搭成一个大正方体,至少需要4×4×4=64个小立方体,所以还需64-10=54个小立方体。 答案:54
交流分享
此类题考查了对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查,如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案。
跟踪练习
1.一个几何的三视图如图所示,则这个几何体是( )
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
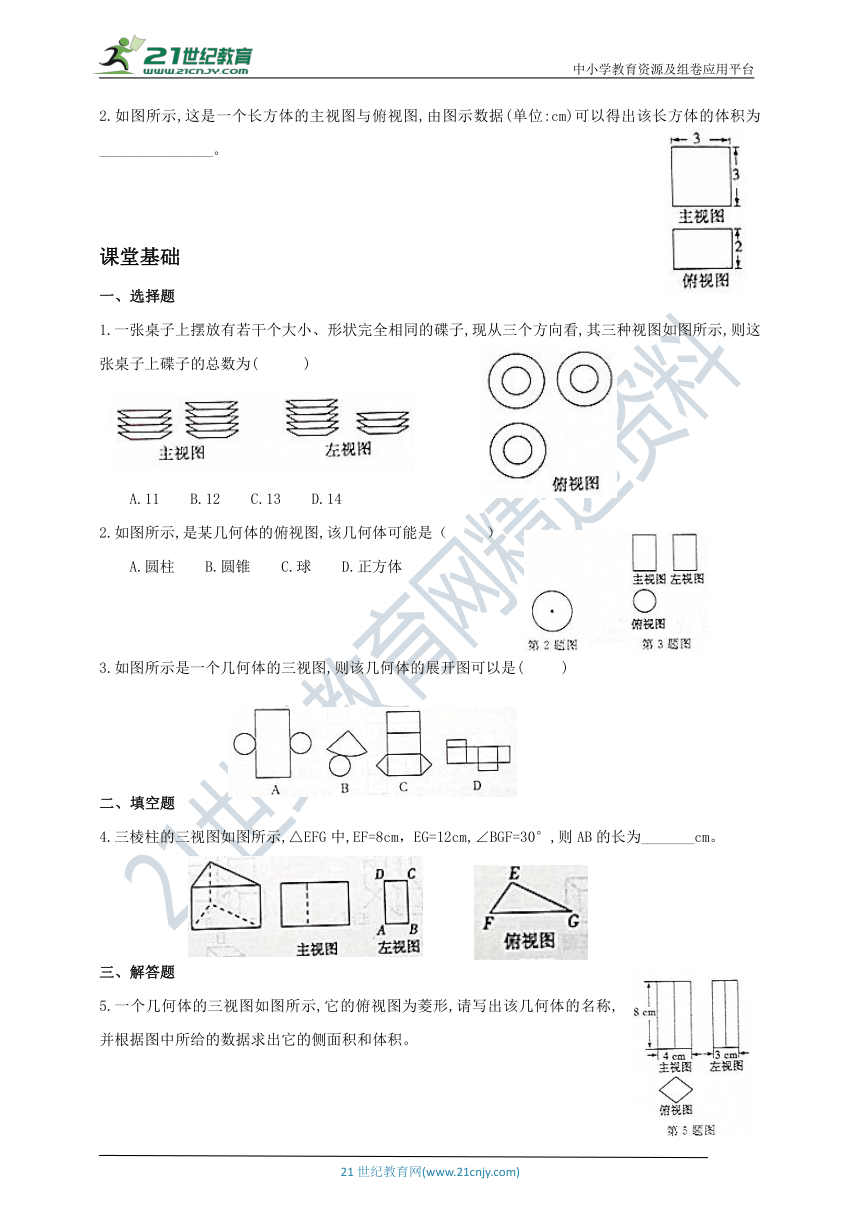
2.如图所示,这是一个长方体的主视图与俯视图,由图示数据(单位:cm)可以得出该长方体的体积为_______________。
课堂基础
一、选择题
1.一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11 B.12 C.13 D.14
2.如图所示,是某几何体的俯视图,该几何体可能是( )
A.圆柱 B.圆锥 C.球 D.正方体
3.如图所示是一个几何体的三视图,则该几何体的展开图可以是( )
二、填空题
4.三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠BGF=30°,则AB的长为_______cm。
三、解答题
5.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的名称,并根据图中所给的数据求出它的侧面积和体积。
四、拓展探究题
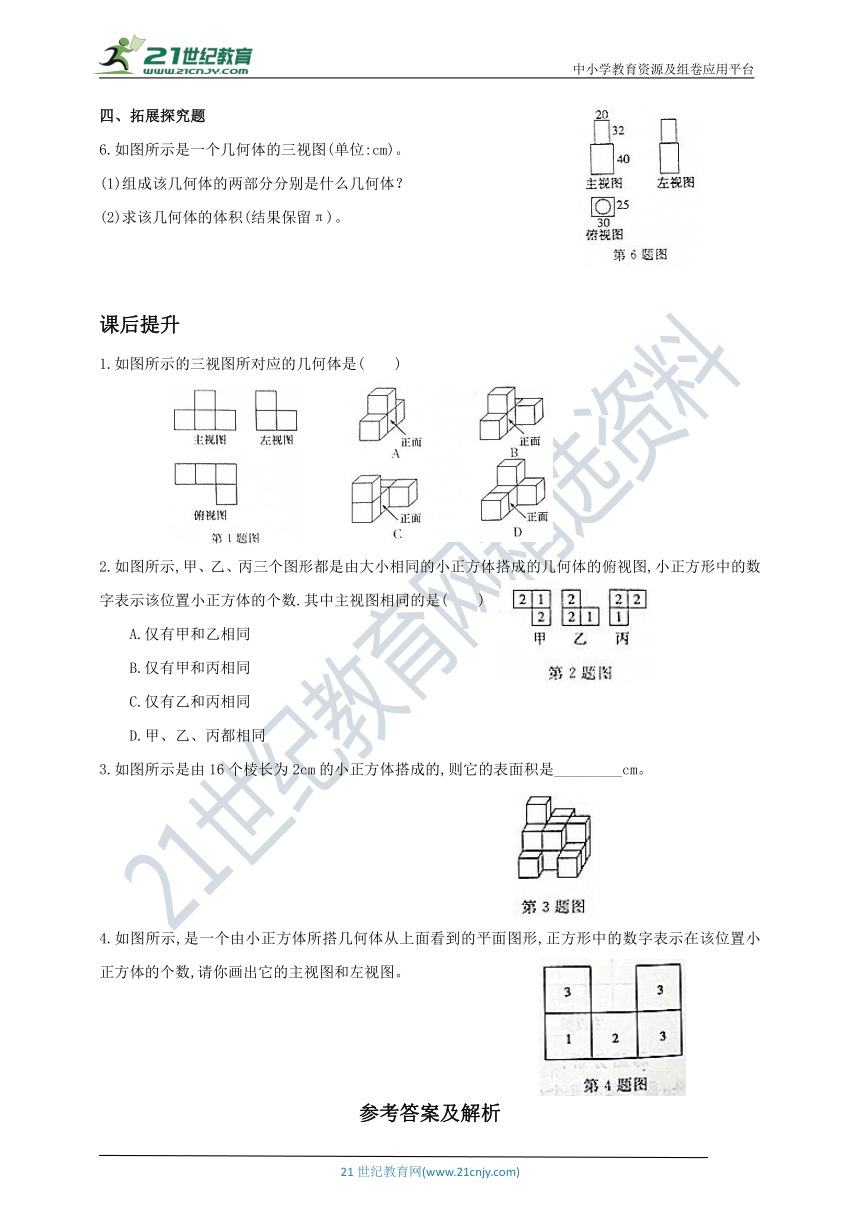
6.如图所示是一个几何体的三视图(单位:cm)。
(1)组成该几何体的两部分分别是什么几何体?
(2)求该几何体的体积(结果保留π)。
课后提升
1.如图所示的三视图所对应的几何体是( )
2.如图所示,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
A.仅有甲和乙相同
B.仅有甲和丙相同
C.仅有乙和丙相同
D.甲、乙、丙都相同
3.如图所示是由16个棱长为2cm的小正方体搭成的,则它的表面积是_________cm。
4.如图所示,是一个由小正方体所搭几何体从上面看到的平面图形,正方形中的数字表示在该位置小正方体的个数,请你画出它的主视图和左视图。
参考答案及解析
课前预习
(1)主视图 俯视图 左视图 (2)主视图 左视图 俯视图
课内探究
跟踪练习 1.D 2. 18cm2
课堂基础
1.B 解析:由俯视图可得:碟子共有3摞,
由几何体的主视图和左视图,可得每摞碟子的个数,如图所示:
故这张桌子上碟子的个数为3+4+5=12(个).
故选B.
2.B 解析:圆柱的俯视图是圆,A错误;圆锥的俯视图是圆,且中心有一个实点,B正确;球的俯视图是圆,C错误;正方体的俯视图是正方形,D错误,故选B.
3.A 解析:∵主视图和左视图是长方形,∴该几何体是柱体,∵俯视图是圆,∴该几何体是圆柱。
∴该几何体的展开图可以是
故选A.
4.6 解析:过点E作EQ⊥FG于点Q,由题意可得出:BQ=AB。
∵ EG=12cm,∠EGF=30°,
∴
故答案为6
5.解:该几何体是直四棱柱.由三视图可知,该几何体底面菱形的对角线的长度分别为4cm,3cm,
∴菱形的边长为,∴该几何体的侧面积为×8×4=80(cm2),
体积为×3×4×8=48(cm3)。
6.解:(1)由题图可知,该几何体的下部分是长方体,上部分是圆柱。
(2)该几何体的体积为30×40×25+π×(20÷2)2×32 (30000+3200π)cm3。
课后提升
1.B 解析:从主、俯视图可判断A,C,D错误,故选B。
2.B 解析:根据分析可知,甲的主视图有2列,每列小正方形数目分别为2,2;乙的主视图有2列,每列小正方形数目分别为2,1;丙的主视图有2列,每列小正方形数目分别为2,2;则主视图相同的是甲和丙,故选B.
4.解:如图所示。
2 视图
第2课时 由三视图还原几何体
课前预习
由三视图还原几何体
(1)在三种视图中____________反映物体的长和高,___________反映物体的长和宽,________反映物体的高和宽。
(2)由三视图复原儿何体,要先分别根据_____________、___________和___________想象立体图形的前面、左侧面和上面,然后再综合在一起想象整体图形。
课内探究
探究要点 由物体的三视图画立体图形
【例】如图所示,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块以搭成一个大正方体,至少还需要_______个小立方块。
思路分析:由三视图易得最底层有7个小立方第二层有2个小立方体,第三层有1个小立方体那么共有7+2-1=10个小立方体,若搭成一个大正方体,至少需要4×4×4=64个小立方体,所以还需64-10=54个小立方体。 答案:54
交流分享
此类题考查了对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查,如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案。
跟踪练习
1.一个几何的三视图如图所示,则这个几何体是( )
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
2.如图所示,这是一个长方体的主视图与俯视图,由图示数据(单位:cm)可以得出该长方体的体积为_______________。
课堂基础
一、选择题
1.一张桌子上摆放有若干个大小、形状完全相同的碟子,现从三个方向看,其三种视图如图所示,则这张桌子上碟子的总数为( )
A.11 B.12 C.13 D.14
2.如图所示,是某几何体的俯视图,该几何体可能是( )
A.圆柱 B.圆锥 C.球 D.正方体
3.如图所示是一个几何体的三视图,则该几何体的展开图可以是( )
二、填空题
4.三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠BGF=30°,则AB的长为_______cm。
三、解答题
5.一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的名称,并根据图中所给的数据求出它的侧面积和体积。
四、拓展探究题
6.如图所示是一个几何体的三视图(单位:cm)。
(1)组成该几何体的两部分分别是什么几何体?
(2)求该几何体的体积(结果保留π)。
课后提升
1.如图所示的三视图所对应的几何体是( )
2.如图所示,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
A.仅有甲和乙相同
B.仅有甲和丙相同
C.仅有乙和丙相同
D.甲、乙、丙都相同
3.如图所示是由16个棱长为2cm的小正方体搭成的,则它的表面积是_________cm。
4.如图所示,是一个由小正方体所搭几何体从上面看到的平面图形,正方形中的数字表示在该位置小正方体的个数,请你画出它的主视图和左视图。
参考答案及解析
课前预习
(1)主视图 俯视图 左视图 (2)主视图 左视图 俯视图
课内探究
跟踪练习 1.D 2. 18cm2
课堂基础
1.B 解析:由俯视图可得:碟子共有3摞,
由几何体的主视图和左视图,可得每摞碟子的个数,如图所示:
故这张桌子上碟子的个数为3+4+5=12(个).
故选B.
2.B 解析:圆柱的俯视图是圆,A错误;圆锥的俯视图是圆,且中心有一个实点,B正确;球的俯视图是圆,C错误;正方体的俯视图是正方形,D错误,故选B.
3.A 解析:∵主视图和左视图是长方形,∴该几何体是柱体,∵俯视图是圆,∴该几何体是圆柱。
∴该几何体的展开图可以是
故选A.
4.6 解析:过点E作EQ⊥FG于点Q,由题意可得出:BQ=AB。
∵ EG=12cm,∠EGF=30°,
∴
故答案为6
5.解:该几何体是直四棱柱.由三视图可知,该几何体底面菱形的对角线的长度分别为4cm,3cm,
∴菱形的边长为,∴该几何体的侧面积为×8×4=80(cm2),
体积为×3×4×8=48(cm3)。
6.解:(1)由题图可知,该几何体的下部分是长方体,上部分是圆柱。
(2)该几何体的体积为30×40×25+π×(20÷2)2×32 (30000+3200π)cm3。
课后提升
1.B 解析:从主、俯视图可判断A,C,D错误,故选B。
2.B 解析:根据分析可知,甲的主视图有2列,每列小正方形数目分别为2,2;乙的主视图有2列,每列小正方形数目分别为2,1;丙的主视图有2列,每列小正方形数目分别为2,2;则主视图相同的是甲和丙,故选B.
4.解:如图所示。
