沪科版九年级数学下册第24章圆单元检测试卷(有答案)
文档属性
| 名称 | 沪科版九年级数学下册第24章圆单元检测试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 214.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-20 18:47:06 | ||
图片预览




文档简介
沪科版九年级数学下册 第24章 圆 单元检测试卷
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 圆柱形油桶的底面半径为0.8??,高为1??,那么这个油桶的侧面积为( )
A.1.6??
??
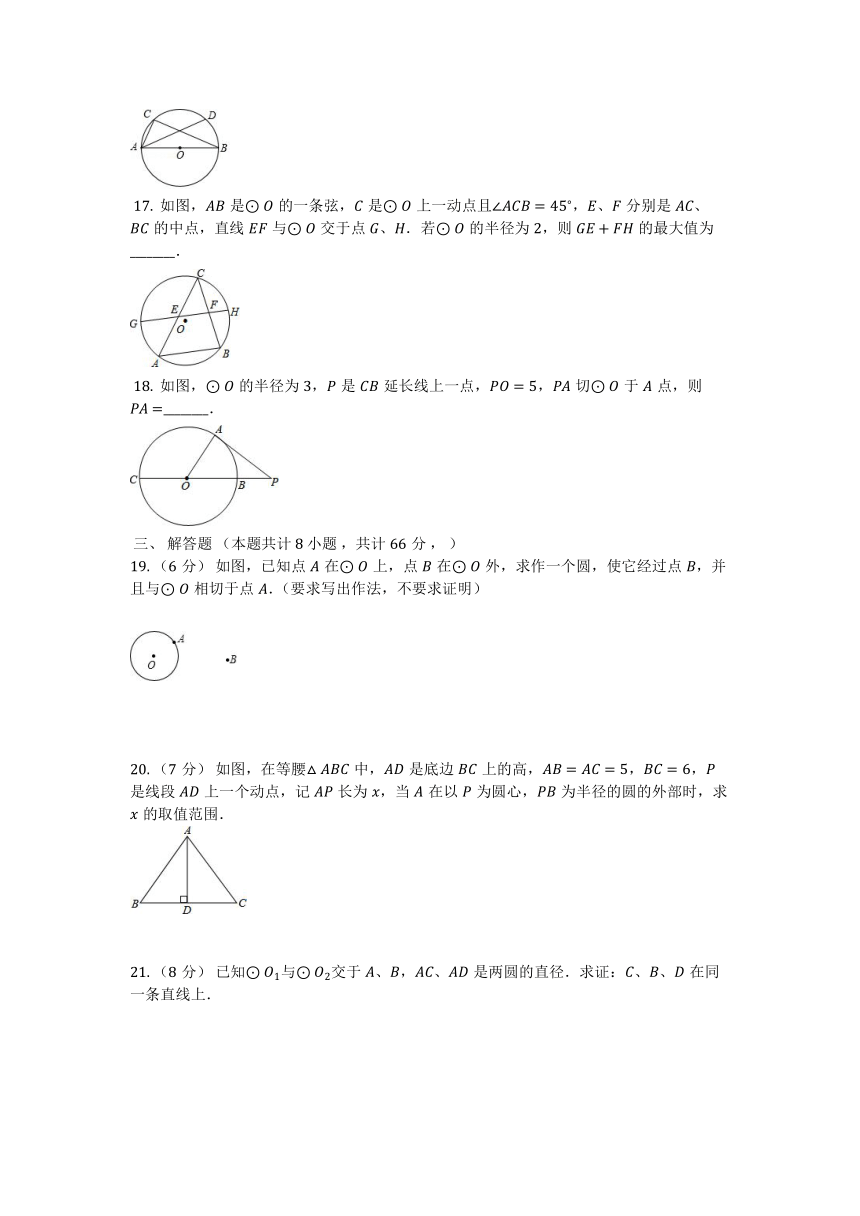
2
B.1.2??
??
2
C.0.64??
??
2
D.0.8??
??
2
?2. 如图,⊙??的弦????交弦????于??,????=4,????=3,????=2,那么????的长为( )
/
A.8
B.6
C.4
D.3
?3. 如图,△??????是由△??????绕点??顺时针旋转
30
°
后得到的图形,若点??恰好落在????上,且∠??????的度数为
100
°
,则∠??????的度数是( )
/
A.
15
°
B.
30
°
C.
38
°
D.
40
°
?4. 如图,已知四边形????????内接于⊙??,????是⊙??的直径,????与⊙??相切于点??,∠??????=
35
°
,则∠??的度数是( )
/
A.
145
°
B.
125
°
C.
90
°
D.
80
°
?5. 已知半径为4的圆??与直线??没有公共点,那么圆心??到直线??的距离??满足( )
A.??=4
B.??>4
C.??<4
D.??≤4
?6. 平面内,下列命题为真命题是( )
A.经过半径外端点的直线是圆的切线
B.经过半径的直线是圆的切线
C.垂直于半径的直线是圆的切线
D.经过半径的外端并且垂直于这条半径的直线是圆的切线
?7. 将△??????绕点??旋转
180
°
得到△??????,则下列作图正确的是( )
A.
/
B.
/
C.
/
D.
/
?8. ????△??????中,∠??=
90
°
,以????为直径的⊙??交????于??,????⊥????交⊙??于??,????交????于??,点??为????延长线上的一点,????延长交????于??,????=????.小华得出3个结论: ①????=????;②????=????;③?????//?????. 其中正确的是( )
/
A.①②
B.①③
C.②③
D.①②③
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
9. 下列说法:①弦是直径;②直径是弦;③过圆心的线段是直径;④一个圆的直径只有一条.其中正确的是________(填序号).
?10. 如图,已知????是圆??的弦,????是圆??的切线,∠??????的平分线交圆??于??,连????并延长交????于点??,若∠??????=
40
°
,则∠??=________度,∠??????=________度.
/
?11. 如图,从点??引⊙??的切线????,????,切点分别为??,??,????切⊙??于??,交????,????于??,??.若△??????的周长为20????,则????=________????.
/
?12. 两边为3和4的直角三角形的内切圆半径为________.
?13. 已知⊙
??
1
与⊙
??
2
内切,⊙
??
1
的半径长是3厘米,圆心距
??
1
??
2
=2厘米,那么⊙
??
2
的半径长等于________厘米.
?14. 如图,????,????是⊙??的弦,????⊥????,????是⊙??的直径.若????=3,则????=________.
/
?15. 如图,在△??????中,∠??=90度.以????为直径作⊙??与斜边????交于点??,且????=3.2????,????=1.8????,则????=________????.
/
?16. 如图,△??????内接于⊙??,????为⊙??的直径,∠??????=
60
°
,弦????平分∠??????,若????=6,则????=________.
/
?17. 如图,????是⊙??的一条弦,??是⊙??上一动点且∠??????=
45
°
,??、??分别是????、????的中点,直线????与⊙??交于点??、??.若⊙??的半径为2,则????+????的最大值为________.
/
?18. 如图,⊙??的半径为3,??是????延长线上一点,????=5,????切⊙??于??点,则????=________.
/
三、 解答题 (本题共计 8 小题 ,共计66分 , )
19. (6分) 如图,已知点??在⊙??上,点??在⊙??外,求作一个圆,使它经过点??,并且与⊙??相切于点??.(要求写出作法,不要求证明)
/
?
20. (7分) 如图,在等腰△??????中,????是底边????上的高,????=????=5,????=6,??是线段????上一个动点,记????长为??,当??在以??为圆心,????为半径的圆的外部时,求??的取值范围.
/
?
21. (8分) 已知⊙
??
1
与⊙
??
2
交于??、??,????、????是两圆的直径.求证:??、??、??在同一条直线上.
/
?22.(9分) 如图,⊙??是△??????的外接圆,????是直径,∠??????=
30
°
,????=1,∠??????的平分线交⊙??于点??,交????于点??.
/
(1)求????,????的长.
(2)廷长????至点??,连接????,当????等于多少时,????与⊙??相切?为什么?
?
23.(9分) 如图,⊙??的直径????的长为2,点??在圆周上,∠??????=
30
°
,点??是圆上一动点,?????//?????交????的延长线于点??,连接????,交????于点??.
(1)如图1,当∠??????=
45
°
时,求证:????是⊙??的切线;
(2)如图2,当点??是????的中点时,求△??????的面积.
/
?
24.(9分) 如图,????是⊙??的直径,⊙??过????的中点??,????⊥????,垂足为??.
/
(1)由这些条件,你能推出哪些正确结论?(要求:不再标注其它字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,写出4个结论即可);
(2)若∠??????为直角,其它条件不变,除上述结论外,你还能推出哪些新的正确结论?并画出图形.〔要求:写出6个结论即可,其它要求同(1)〕
?25.(9分) 如图,????是⊙??的切线,点??在直径????的延长线上.
(1)求证:∠??????=∠??????;
(2)若????=
2
3
????,????=3,求????的长.
/
?
26.(9分) 如图1、图2、图3,在矩形????????中,??是????边上的一点,以????为边作平行四边形????????,使点??在????的对边????上,
(1)如图1,试说明:平行四边形????????的面积与矩形????????的面积相等;
(2)如图2,若平行四边形????????是矩形,????与????交于点??,试说明:??、??、??、??四点在同一个圆上;
(3)如图3,若????/
答案
1. A
2. B
3. D
4. B
5. B
6. D
7. D
8. D
9. ②
10. 4080
11. 10
12. 1或
7
?1
2
13. 5或1
14. 3
15. 4
16. 2
3
17. 4?
2
18. 4
19. 解:如图, ①连接????、????, ②作线段????的垂直平分线交????的延长线于一点,交点即为??′, ③以??′为圆心,??′??或??′??的长度为半径作圆, ④⊙??′即为所求.
/
20. 解:如图,
/
在等腰△??????中, ∵????是底边????上的高,????=????=5,????=6, ∴????=????=3, 在????△??????中,由勾股定理可得: ????=
??
??
2
???
??
2
=4, ∵????长为??, ∴????=4???, 当????=????时, 在????△??????中,由勾股定理得:
3
2
+(4???
)
2
=
??
2
, 解得:??=
25
8
, ∵当??在以??为圆心,????为半径的圆的外部时,????>????, ∴??>
25
8
, ∵??≤4, ∴
25
8
21. 证明:连接????、????、????,如下图所示:
/
.∵????、????是两圆的直径,??为两圆的交点, ∴∠??????,∠??????均为直角, ∴????⊥????,????⊥????, ∴?????//?????; ∵????与????交于??点, ∴????与????共线, ∴??、??、??在同一条直线上.
22. 解:(1)如图1,连接????,
/
∵????是直径, ∴∠??????=∠??????=
90
°
, 在????△??????中, ∵∠??????=
30
°
,????=1, ∴????=2, ∴????=
??
??
2
???
??
2
=
2
2
?
1
2
=
3
, ∵????平分∠??????, ∴△??????为等腰直角三角形, ∴????=????=
2
2
????=
2
;(2)如图2,连接????,
/
∵∠??????=
30
°
, ∴∠??????=
60
°
, ∴△??????为等边三角形, 当????为⊙??的切线时,则∠??????=
90
°
, ∴∠??????=∠??????=
30
°
, ∴????=????=1, 即当????=1时,????与⊙??相切.
23. (1)证明:如图1中,连接????.
/
∵∠??=
45
°
, ∴∠??????=2∠??=
90
°
, ∵?????//?????, ∴∠??????+∠??????=
180
°
, ∴∠??????=
90
°
, ∴????⊥????, ∴????是⊙??切线.(2)解:如图2中,连接????, ∵????=????, ∴????⊥????, ∴????=????, ∴∠??????=∠??????, ∵?????//?????, ∴????⊥????, ∴∠??????=
90
°
,
/
在????△??????中,∵∠??????=
90
°
,∠??????=
30
°
,????=2, ∴????=1,????=
3
, ∴????=
1
2
????=
3
2
,????=2????=
3
, 在????△??????中, ∵∠??????=
90
°
,????=
3
,∠??=∠??????=
30
°
, ∴????=2????=2
3
,????=
??
??
2
???
??
2
=3, ∴
??
△??????
=
1
2
??????????=
3
3
2
.
24. 解:(1)①????是⊙??的切线, ②????=????, ③∠??=∠??, ④??
??
2
=?????????, ⑤??
??
2
=?????????, ⑥∠??+∠??????=
90
°
, ⑦??
??
2
+??
??
2
=??
??
2
; 以上结论可任意选择. 证明:连接????、????; ∵??、??分别是????、????的中点, ∴????是△??????的中位线,则?????//?????; ∵????⊥????,∴????⊥????,即????是⊙??的切线;① ∵????是⊙??的直径,∴∠??????=
90
°
; ∵??是????的中点,∴????垂直平分????; ∴????=????②,∠??=∠??③; 在????△??????中,????⊥????,由射影定理得:??
??
2
=?????????⑤,??
??
2
=?????????④; 在????△??????中,????⊥????,则∠??+∠??????=
90
°
,由勾股定理得??
??
2
=??
??
2
+??
??
2
⑦; (2)①????=????,②????=????, ③????=????,④?????//?????, ⑤????是⊙??的切线,⑥????=
1
2
????, ⑦∠??=∠??????=
45
°
, ⑧∠??=∠??????=
45
°
, ⑨??
??
2
=?????????, ⑩
????
????
=
????
????
=
????
????
, (11)??
??
2
+??
??
2
=??
??
2
(12)
????
????
=
????
????
; 证明:∵∠??????=
90
°
,且????是⊙??的直径, ∴????是⊙??的切线;⑤ ∵????⊥????,????⊥????, ∴?????//?????;④ ∴
????
????
=
????
????
=
????
????
⑩,
????
????
=
????
????
;(12) ∵??是????的中点, ∴????是△??????的中位线,得????=????①,????=
1
2
????⑥; 在????△??????中,??是斜边????的中点,则????=????②,????=????③; 由(1)易知△??????是等腰直角三角形,则∠??=∠??????=
45
°
⑦,∠??=∠??????=
45
°
⑧; 在????△??????中,∠??????=
90
°
,由勾股定理得??
??
2
+??
??
2
=??
??
2
(11); 由于????⊥????,由射影定理得??
??
2
=?????????⑨.
/
25. 证明:连接????,如图所示. ∵????=????, ∴∠??????=∠??????. ∵????是⊙??的切线,????是⊙??的半径, ∴∠??????+∠??????=
90
°
. ∵????是⊙??的直径, ∴∠??????=
90
°
, ∴∠??????+∠??????=
90
°
, ∴∠??????=∠??????.∵∠??=∠??,∠??????=∠??????, ∴△??????∽△??????, ∴
????
????
=
????
????
. ∵????=
2
3
????, ∴
????
????
=
2
3
, ∴
????
????
=
2
3
, 又∵????=3, ∴????=2.
/
26. 解:(1)过??点作????垂直????于点??;
??
????????
=????×????,
??
????????
=????×????=
????
cos∠??????
×(????×cos∠??????), ∠??????=∠??????, 所以
??
????????
=????×????, 所以,
??
????????
=
??
????????
.(2)因为平行四边形????????是矩形,四边形????????也是矩形; 所以∠??????=∠??????=
90
°
, 则∠??????+∠??????=
180
°
, 所以??、??、??、??四点在同一个圆上.(3)相切. 过??作????⊥????于??; ∵∠2+∠3=
90
°
,∠1+∠2=
90
°
, ∴∠3=∠1,∠2=∠4, ∴△??????∽△??????, ∵??是????的中点, ∴
????
????
=
????
????
=
????
????
=2, 在△??????与△??????中,
????
????
=
????
????
=
????
????
=2; ∵????=????, ∴
????
????
=
????
????
=2, ∵∠??????=∠??????=
90
°
, ∴△??????∽△??????∽△??????,∴∠1=∠??????,即????是∠??????的平分线, ∴????=????=????,∵????=????,∠??????=∠??????=
90
°
, ∴以????为直径的圆与直线????相切.
/
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 圆柱形油桶的底面半径为0.8??,高为1??,那么这个油桶的侧面积为( )
A.1.6??
??
2
B.1.2??
??
2
C.0.64??
??
2
D.0.8??
??
2
?2. 如图,⊙??的弦????交弦????于??,????=4,????=3,????=2,那么????的长为( )
/
A.8
B.6
C.4
D.3
?3. 如图,△??????是由△??????绕点??顺时针旋转
30
°
后得到的图形,若点??恰好落在????上,且∠??????的度数为
100
°
,则∠??????的度数是( )
/
A.
15
°
B.
30
°
C.
38
°
D.
40
°
?4. 如图,已知四边形????????内接于⊙??,????是⊙??的直径,????与⊙??相切于点??,∠??????=
35
°
,则∠??的度数是( )
/
A.
145
°
B.
125
°
C.
90
°
D.
80
°
?5. 已知半径为4的圆??与直线??没有公共点,那么圆心??到直线??的距离??满足( )
A.??=4
B.??>4
C.??<4
D.??≤4
?6. 平面内,下列命题为真命题是( )
A.经过半径外端点的直线是圆的切线
B.经过半径的直线是圆的切线
C.垂直于半径的直线是圆的切线
D.经过半径的外端并且垂直于这条半径的直线是圆的切线
?7. 将△??????绕点??旋转
180
°
得到△??????,则下列作图正确的是( )
A.
/
B.
/
C.
/
D.
/
?8. ????△??????中,∠??=
90
°
,以????为直径的⊙??交????于??,????⊥????交⊙??于??,????交????于??,点??为????延长线上的一点,????延长交????于??,????=????.小华得出3个结论: ①????=????;②????=????;③?????//?????. 其中正确的是( )
/
A.①②
B.①③
C.②③
D.①②③
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
9. 下列说法:①弦是直径;②直径是弦;③过圆心的线段是直径;④一个圆的直径只有一条.其中正确的是________(填序号).
?10. 如图,已知????是圆??的弦,????是圆??的切线,∠??????的平分线交圆??于??,连????并延长交????于点??,若∠??????=
40
°
,则∠??=________度,∠??????=________度.
/
?11. 如图,从点??引⊙??的切线????,????,切点分别为??,??,????切⊙??于??,交????,????于??,??.若△??????的周长为20????,则????=________????.
/
?12. 两边为3和4的直角三角形的内切圆半径为________.
?13. 已知⊙
??
1
与⊙
??
2
内切,⊙
??
1
的半径长是3厘米,圆心距
??
1
??
2
=2厘米,那么⊙
??
2
的半径长等于________厘米.
?14. 如图,????,????是⊙??的弦,????⊥????,????是⊙??的直径.若????=3,则????=________.
/
?15. 如图,在△??????中,∠??=90度.以????为直径作⊙??与斜边????交于点??,且????=3.2????,????=1.8????,则????=________????.
/
?16. 如图,△??????内接于⊙??,????为⊙??的直径,∠??????=
60
°
,弦????平分∠??????,若????=6,则????=________.
/
?17. 如图,????是⊙??的一条弦,??是⊙??上一动点且∠??????=
45
°
,??、??分别是????、????的中点,直线????与⊙??交于点??、??.若⊙??的半径为2,则????+????的最大值为________.
/
?18. 如图,⊙??的半径为3,??是????延长线上一点,????=5,????切⊙??于??点,则????=________.
/
三、 解答题 (本题共计 8 小题 ,共计66分 , )
19. (6分) 如图,已知点??在⊙??上,点??在⊙??外,求作一个圆,使它经过点??,并且与⊙??相切于点??.(要求写出作法,不要求证明)
/
?
20. (7分) 如图,在等腰△??????中,????是底边????上的高,????=????=5,????=6,??是线段????上一个动点,记????长为??,当??在以??为圆心,????为半径的圆的外部时,求??的取值范围.
/
?
21. (8分) 已知⊙
??
1
与⊙
??
2
交于??、??,????、????是两圆的直径.求证:??、??、??在同一条直线上.
/
?22.(9分) 如图,⊙??是△??????的外接圆,????是直径,∠??????=
30
°
,????=1,∠??????的平分线交⊙??于点??,交????于点??.
/
(1)求????,????的长.
(2)廷长????至点??,连接????,当????等于多少时,????与⊙??相切?为什么?
?
23.(9分) 如图,⊙??的直径????的长为2,点??在圆周上,∠??????=
30
°
,点??是圆上一动点,?????//?????交????的延长线于点??,连接????,交????于点??.
(1)如图1,当∠??????=
45
°
时,求证:????是⊙??的切线;
(2)如图2,当点??是????的中点时,求△??????的面积.
/
?
24.(9分) 如图,????是⊙??的直径,⊙??过????的中点??,????⊥????,垂足为??.
/
(1)由这些条件,你能推出哪些正确结论?(要求:不再标注其它字母,找结论的过程中所连辅助线不能出现在结论中,不写推理过程,写出4个结论即可);
(2)若∠??????为直角,其它条件不变,除上述结论外,你还能推出哪些新的正确结论?并画出图形.〔要求:写出6个结论即可,其它要求同(1)〕
?25.(9分) 如图,????是⊙??的切线,点??在直径????的延长线上.
(1)求证:∠??????=∠??????;
(2)若????=
2
3
????,????=3,求????的长.
/
?
26.(9分) 如图1、图2、图3,在矩形????????中,??是????边上的一点,以????为边作平行四边形????????,使点??在????的对边????上,
(1)如图1,试说明:平行四边形????????的面积与矩形????????的面积相等;
(2)如图2,若平行四边形????????是矩形,????与????交于点??,试说明:??、??、??、??四点在同一个圆上;
(3)如图3,若????/
答案
1. A
2. B
3. D
4. B
5. B
6. D
7. D
8. D
9. ②
10. 4080
11. 10
12. 1或
7
?1
2
13. 5或1
14. 3
15. 4
16. 2
3
17. 4?
2
18. 4
19. 解:如图, ①连接????、????, ②作线段????的垂直平分线交????的延长线于一点,交点即为??′, ③以??′为圆心,??′??或??′??的长度为半径作圆, ④⊙??′即为所求.
/
20. 解:如图,
/
在等腰△??????中, ∵????是底边????上的高,????=????=5,????=6, ∴????=????=3, 在????△??????中,由勾股定理可得: ????=
??
??
2
???
??
2
=4, ∵????长为??, ∴????=4???, 当????=????时, 在????△??????中,由勾股定理得:
3
2
+(4???
)
2
=
??
2
, 解得:??=
25
8
, ∵当??在以??为圆心,????为半径的圆的外部时,????>????, ∴??>
25
8
, ∵??≤4, ∴
25
8
21. 证明:连接????、????、????,如下图所示:
/
.∵????、????是两圆的直径,??为两圆的交点, ∴∠??????,∠??????均为直角, ∴????⊥????,????⊥????, ∴?????//?????; ∵????与????交于??点, ∴????与????共线, ∴??、??、??在同一条直线上.
22. 解:(1)如图1,连接????,
/
∵????是直径, ∴∠??????=∠??????=
90
°
, 在????△??????中, ∵∠??????=
30
°
,????=1, ∴????=2, ∴????=
??
??
2
???
??
2
=
2
2
?
1
2
=
3
, ∵????平分∠??????, ∴△??????为等腰直角三角形, ∴????=????=
2
2
????=
2
;(2)如图2,连接????,
/
∵∠??????=
30
°
, ∴∠??????=
60
°
, ∴△??????为等边三角形, 当????为⊙??的切线时,则∠??????=
90
°
, ∴∠??????=∠??????=
30
°
, ∴????=????=1, 即当????=1时,????与⊙??相切.
23. (1)证明:如图1中,连接????.
/
∵∠??=
45
°
, ∴∠??????=2∠??=
90
°
, ∵?????//?????, ∴∠??????+∠??????=
180
°
, ∴∠??????=
90
°
, ∴????⊥????, ∴????是⊙??切线.(2)解:如图2中,连接????, ∵????=????, ∴????⊥????, ∴????=????, ∴∠??????=∠??????, ∵?????//?????, ∴????⊥????, ∴∠??????=
90
°
,
/
在????△??????中,∵∠??????=
90
°
,∠??????=
30
°
,????=2, ∴????=1,????=
3
, ∴????=
1
2
????=
3
2
,????=2????=
3
, 在????△??????中, ∵∠??????=
90
°
,????=
3
,∠??=∠??????=
30
°
, ∴????=2????=2
3
,????=
??
??
2
???
??
2
=3, ∴
??
△??????
=
1
2
??????????=
3
3
2
.
24. 解:(1)①????是⊙??的切线, ②????=????, ③∠??=∠??, ④??
??
2
=?????????, ⑤??
??
2
=?????????, ⑥∠??+∠??????=
90
°
, ⑦??
??
2
+??
??
2
=??
??
2
; 以上结论可任意选择. 证明:连接????、????; ∵??、??分别是????、????的中点, ∴????是△??????的中位线,则?????//?????; ∵????⊥????,∴????⊥????,即????是⊙??的切线;① ∵????是⊙??的直径,∴∠??????=
90
°
; ∵??是????的中点,∴????垂直平分????; ∴????=????②,∠??=∠??③; 在????△??????中,????⊥????,由射影定理得:??
??
2
=?????????⑤,??
??
2
=?????????④; 在????△??????中,????⊥????,则∠??+∠??????=
90
°
,由勾股定理得??
??
2
=??
??
2
+??
??
2
⑦; (2)①????=????,②????=????, ③????=????,④?????//?????, ⑤????是⊙??的切线,⑥????=
1
2
????, ⑦∠??=∠??????=
45
°
, ⑧∠??=∠??????=
45
°
, ⑨??
??
2
=?????????, ⑩
????
????
=
????
????
=
????
????
, (11)??
??
2
+??
??
2
=??
??
2
(12)
????
????
=
????
????
; 证明:∵∠??????=
90
°
,且????是⊙??的直径, ∴????是⊙??的切线;⑤ ∵????⊥????,????⊥????, ∴?????//?????;④ ∴
????
????
=
????
????
=
????
????
⑩,
????
????
=
????
????
;(12) ∵??是????的中点, ∴????是△??????的中位线,得????=????①,????=
1
2
????⑥; 在????△??????中,??是斜边????的中点,则????=????②,????=????③; 由(1)易知△??????是等腰直角三角形,则∠??=∠??????=
45
°
⑦,∠??=∠??????=
45
°
⑧; 在????△??????中,∠??????=
90
°
,由勾股定理得??
??
2
+??
??
2
=??
??
2
(11); 由于????⊥????,由射影定理得??
??
2
=?????????⑨.
/
25. 证明:连接????,如图所示. ∵????=????, ∴∠??????=∠??????. ∵????是⊙??的切线,????是⊙??的半径, ∴∠??????+∠??????=
90
°
. ∵????是⊙??的直径, ∴∠??????=
90
°
, ∴∠??????+∠??????=
90
°
, ∴∠??????=∠??????.∵∠??=∠??,∠??????=∠??????, ∴△??????∽△??????, ∴
????
????
=
????
????
. ∵????=
2
3
????, ∴
????
????
=
2
3
, ∴
????
????
=
2
3
, 又∵????=3, ∴????=2.
/
26. 解:(1)过??点作????垂直????于点??;
??
????????
=????×????,
??
????????
=????×????=
????
cos∠??????
×(????×cos∠??????), ∠??????=∠??????, 所以
??
????????
=????×????, 所以,
??
????????
=
??
????????
.(2)因为平行四边形????????是矩形,四边形????????也是矩形; 所以∠??????=∠??????=
90
°
, 则∠??????+∠??????=
180
°
, 所以??、??、??、??四点在同一个圆上.(3)相切. 过??作????⊥????于??; ∵∠2+∠3=
90
°
,∠1+∠2=
90
°
, ∴∠3=∠1,∠2=∠4, ∴△??????∽△??????, ∵??是????的中点, ∴
????
????
=
????
????
=
????
????
=2, 在△??????与△??????中,
????
????
=
????
????
=
????
????
=2; ∵????=????, ∴
????
????
=
????
????
=2, ∵∠??????=∠??????=
90
°
, ∴△??????∽△??????∽△??????,∴∠1=∠??????,即????是∠??????的平分线, ∴????=????=????,∵????=????,∠??????=∠??????=
90
°
, ∴以????为直径的圆与直线????相切.
/
