函数单调性课件（共23张PPT）

课件23张PPT。我看见，一座座山，一座座山川，一座座山川相连...Oxy§3函数的单调性1.理解函数单调性的定义；（重点）
2.掌握用定义判断函数单调性的方法及步骤；（难点）
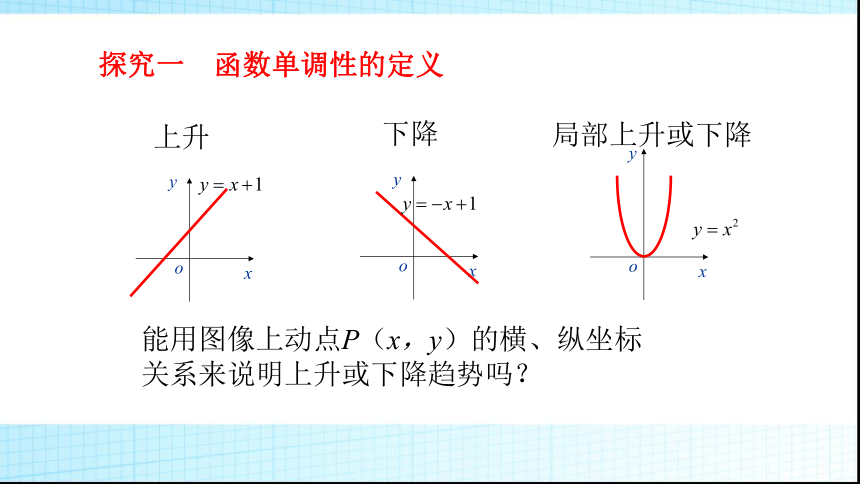
3.会用函数单调性的定义证明简单的函数的单调性，求函数的单调区间.学习目标探究一 函数单调性的定义1、画出下列函数的图像
（1）y=x+1;
（2）y=-x+1;
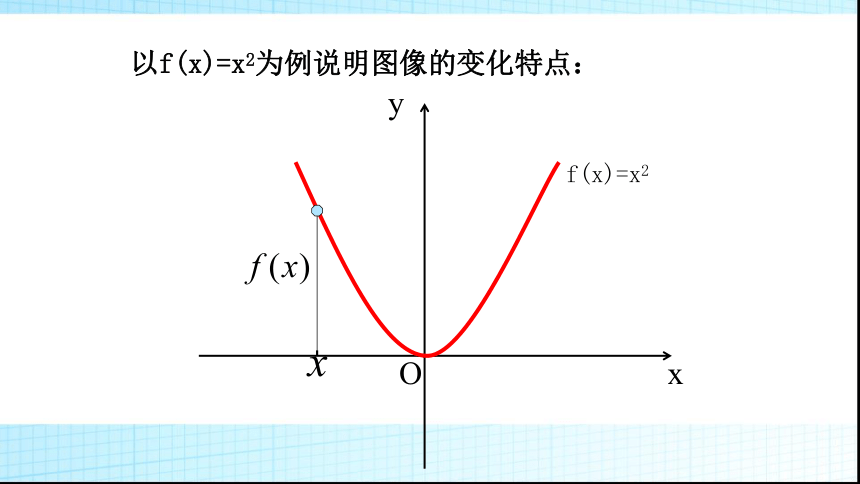
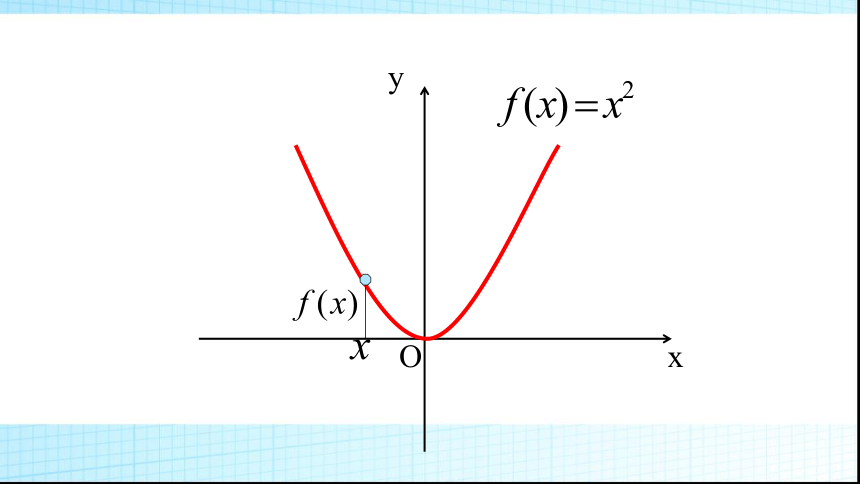
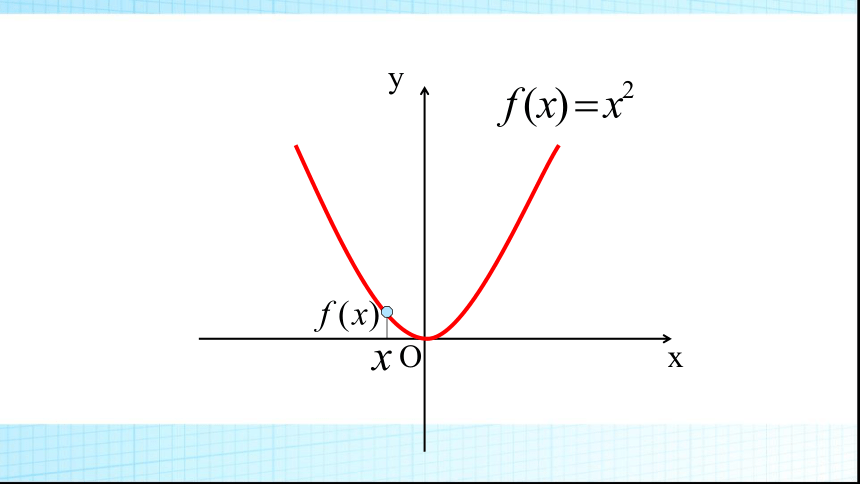
（3）y=x2;推进新课能用图像上动点P（x，y）的横、纵坐标关系来说明上升或下降趋势吗？局部上升或下降下降上升探究一 函数单调性的定义Oxy以f(x)=x2为例说明图像的变化特点：f(x)=x2OxyOxyOxyOxyOxyOxyOxyOxyxyO（-∞，0]上 随x的增大而减小;[0，+∞）上 随x的增大而增大. 那么就说函数f(x)在区间A上是递减的（减函数），A称为f(x)的单调减区间 .你能类比增函数的研究方法定义减函数吗？设函数y=f(x)的定义域为I： 如果对于定义域I内某个区间A上
的任意两个自变量的值x1,x2，如果对于定义域I内某个区间A上
的任意两个自变量的值x1,x2， 那么就说函数f(x)在区间A上是递增的（增函数），A称为f(x)的单调增区间.当x1单调区间设函数y=f(x)的定义域为I：增函数的定义.如果对于定义域I内某个区间A上
的任意两个自变量的值x1,x2，设函数y=f(x)的定义域为I： （1）如果函数 y =f(x)在区间I内是单调增函数或单调减函数，
那么就说函数 y =f(x)在区间I上具有单调性.
在单调区间上，增函数的图像是上升的，减函数的图像是下降的.
（2）函数单调性是针对某个区间而言的，是一个局部性质;
（3）x1, x2 取值的任意性.【特别提醒】例1、画出反比例函数 = 的图像.
（1）这个函数的定义域I是什么？
（2）它在定义域I上的单调性是怎样的？用定义证明你的结论.函数图象如图根据函数单调性的定义，结合函数的图象可知上述说法是错误的.【思考交流】①取值：即设x1、x2是该区间内的任意两个值,且x1②作差变形：即作差f(x1)-f(x2)(或f(x2)-f(x1)),
并用因式分解、配方、有理化等方法将差式向有利于判断差的符号的方向变形;
③定号：确定差f(x1)-f(x2)(或f(x2)-f(x1))的符号,当符号不确定时,可进行分类讨论;
④判断：根据定义得出结论.利用定义证明或判断函数在指定区间上的单调性的步骤:【提升总结】此为证明的关键点、易错点想一想你学到了什么知识？？掌握了什么方法？收获了什么思想？？？取 值 → 作 差 变 形 → 定 号 → 下结论 证明步骤函数的单调性是函数在其定义域上的“局部”性质，即函数可能在其定义域上的某个区间内递增，在另外的区间上递减，研究函数的单调性一定要注意在定义域的哪个区间内.关注