4.3一次函数的图象课件 (共37张PPT)
文档属性
| 名称 | 4.3一次函数的图象课件 (共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 560.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-23 12:14:08 | ||
图片预览








文档简介
课件37张PPT。一天,小明以80米 /分的速度去上学,请问小明离家的距离S(米)与小明出发的时间t(分)之间的函数关系式是怎样的?它是一次函数吗?它是正比例函数吗? S=80t(t≥0)
下面的图象能表示上面问题中的S与t的关系吗?
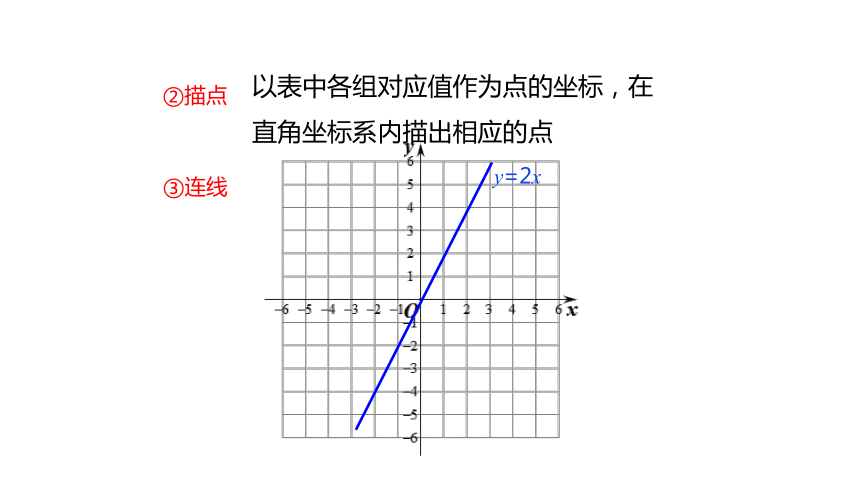
我们说,上面的图象是函数S=80t(t≥0)的图象,这就是我们今天要学习的主要内容:一次函数的图象的特殊情况正比例函数的图象。引入课题1.在下列函数2.函数有哪些表示方法?图象法、列表法、关系式法是一次函数的是 ,是正比例函数的是 .(2),(4)(2)三种方法可以相互转化它们之间有什么关系?3.你能将关系式法转化成图象法吗?什么是函数的图象?例1:画出下面正比例函数y=2x的图象.解:
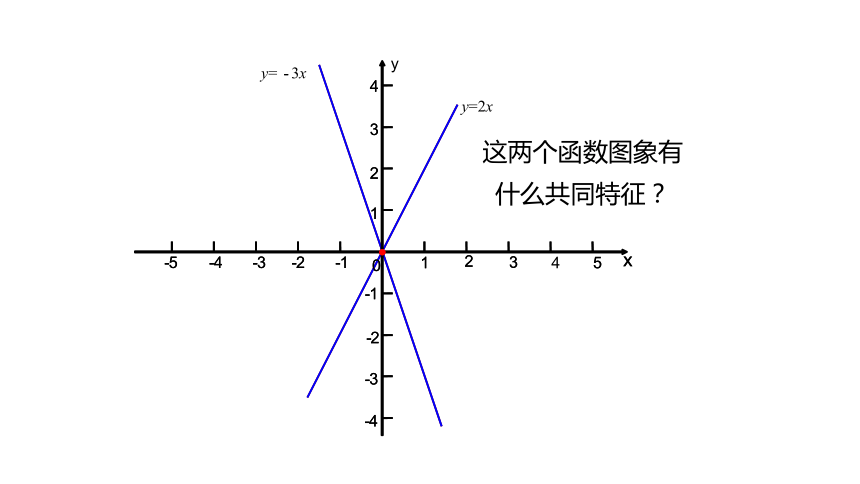
xy100-12-2…………24-2-4关系式法列表法①列表典例精析y=2x②描点以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点③连线画函数图象的一般步骤:①列表②描点③连线根据这个步骤画出函数y=-3x的图象要点归纳这两个函数图象有什么共同特征?y1245-1-2-3-4-5-1-2-3-41430y=-3x32x125-1-2-3-4-5-1-2-3-41430-32xy=2x归纳总结由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.两点
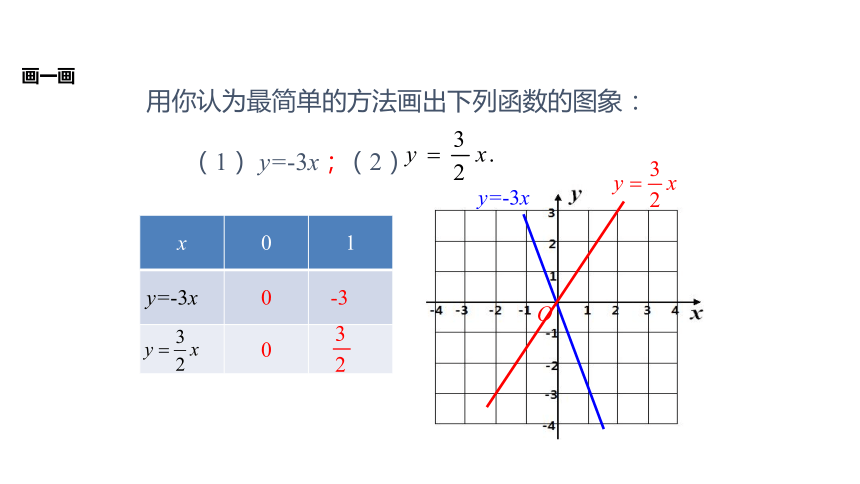
作图法O用你认为最简单的方法画出下列函数的图象:
(1) y=-3x;(2)0-30y=-3x画一画例2 已知正比例函数y=(m+1)xm2 ,它的图象经过第几象限?m+1=2>0该函数是正比例函数∴根据正比例函数的性质,k>0可得该图象经过一、三象限.解:(1)若函数图象经过第一、三象限,则k的取值
范围是________.变式1: 已知正比例函数y=(k+1)x.k>-1(2)若函数图象经过点(2,4),则k_____.解析:因为函数图象经过第一、三象限,所以
k+1>0,解得k>-1.解析:将坐标(2,4)带入函数表达式中,得
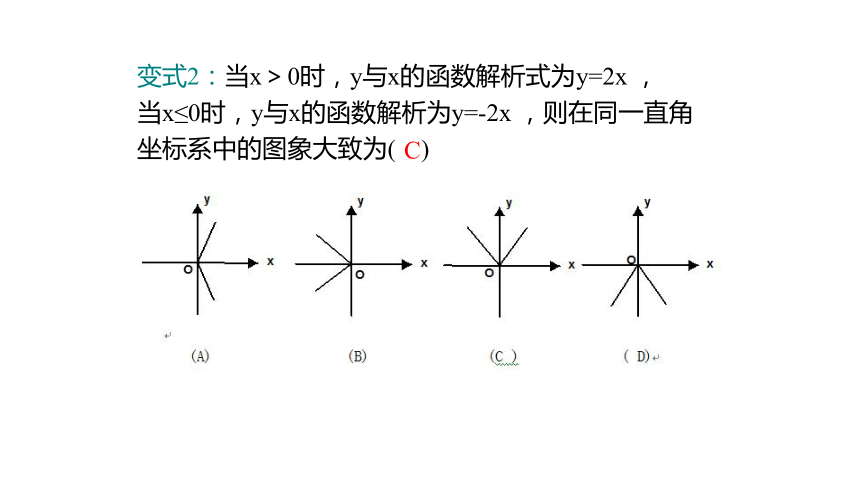
4=(k+1)·2,解得k=1.=1变式2:当x>0时,y与x的函数解析式为y=2x ,
当x≤0时,y与x的函数解析为y=-2x ,则在同一直角
坐标系中的图象大致为( ) C画一画:在同一直角坐标系内画出正比例函数 y=x , y=3x, y=- x和 y=-4x 的图象. 这四个函数中,随着x的增大,y的值分别如何变化?当k>0时,x增大时,y的值也增大;当k<0时,x增大时,y的值反而减小.24 y = 2x 1224y随x的增大而增大y随x的增大而减小-3-6想一想:下列函数中,随着x的增大,y的值分别如何变化?在正比例函数y=kx中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.总结归纳(1)正比例函数y=x和y=3x中,随着x值的增大,y的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
(2)正比例函数y=- x和y=-4x中,随着x值的增大,y的值都减小了,其中哪一个减小得更快?你是如何判断的?|k|越大,直线越陡,直线越靠近y轴.练一练 1.已知正比例函数y=kx (k>0)的图象上有两点(x1,y1),
(x2,y2),若x1A k1>k2 B k1=k2
C k1所以4=m·m,解得m=±2.
又y的值随着x值的增大而减小,
所以m<0,故m=-2.正比例函数的图象和性质图象:经过原点的直线.
当k>0时,经过第一、三象限;
当k<0时,经过第二、四象限.性质:当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.画正比例函数图象的一般步骤:列表、描点、连线正比例函数 解析式 y =kx(k≠0) 性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.一次函数解析式 y =kx+b(k≠0) 针对函数 y =kx+b,大家想研究什么?应该怎样研究? 在上一课的学习中,我们学会了正比例函数图象的画法,分为三个步骤.①列表②描点③连线 那么你能用同样的方法画出一次函数的图象吗? -3 -2 -154321 o-2-3-4-5 2 3 4 5xy 1y=-2x+1描点、
连线一次函数的图象
是什么?-1 列表例1:画出一次函数y=-2x+1的图象一次函数总结归纳一次函数y=kx+b的图象也称为直线y=kx+b. 一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过
(0,b)和(1,k+b)或( ,0)O 用你认为最简单的方法画出下列函数的图象:
(1) y=-2x-1;(2) y=0.5x+1-1-31y=-2x-1做一做1.5y=0.5x+1也可以先画直线 y=-2x与 y=0.5x,再分别平移它们,也能得到直线y=-2x-1与 y=0.5x+1....xy2O...活动:请大家用描点法在同一坐标系内画出一次函数y=x+2,y=x-2的图象.0-31-42-23-140...y=x+2y=x-2思考:观察它们的图象有什么特点?y=xy=x+2y=x-2y2O●●观察三个函数图象的平移情况:探究归纳 把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1. 这三个函数的图象形状都是 ,并且倾斜程度
______.
2. 函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移
个单位长度而得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向____ 平移____个单位长度而得到.直线相同(0,2)上2(0,-2)下2 比较三个函数的解析式, 相同,
它们的图象的位置关系是 . 自变量系数k平行 一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).下上思考:与x轴的交点坐标是什么?要点归纳(1)将直线y=2x向上平移2个单位后所得图象对应的函数表达式为( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
(2)将正比例函数y=-6x的图象向上平移,则平移后所得图象对应的函数表达式可能是__________
(写出一个即可).练一练B y=-6x+3画一画1:在同一坐标系中作出下列函数的图象.(1)(2)(3)-3O-223123-1-1-2xy1思考:k,b的值跟图象有什么关系?画一画2: 在同一坐标系中作出下列函数的图象.(1)(2)(3)-3o-223123-1-1-2xy1思考:k,b的值跟图象有什么关系?在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.由此得到一次函数性质:归纳总结例2 P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象
上的两点,下列判断中,正确的是( )A.y1>y2 C.当x1<x2时,y1<y2 B. y1<y2 D.当x1<x2时,y1>y2 D解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.提示:反过来也成立:y越大,x也越大.k 0,b 0>>k 0,b 0k 0,b 0k 0,b 0k 0,b 0k 0,b 0>>><<<<<==思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:归纳总结 一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.① b>0时,直线经过 一、二、四象限;② b<0时,直线经过二、三、四象限.① b>0时,直线经过一、二、三象限; ② b<0时,直线经过一、三、四象限.两个一次函数y1=ax+b与y2=bx+a,它们在同一坐标系中的图象可能是( )练一练C 例3 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;解:(1)由题意得1-2m>0,解得(2)由题意得1-2m≠0且m-1<0,即(3)由题意得1-2m<0且m-1<0,解得一次函数函数的图象和性质当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.图象性质
下面的图象能表示上面问题中的S与t的关系吗?
我们说,上面的图象是函数S=80t(t≥0)的图象,这就是我们今天要学习的主要内容:一次函数的图象的特殊情况正比例函数的图象。引入课题1.在下列函数2.函数有哪些表示方法?图象法、列表法、关系式法是一次函数的是 ,是正比例函数的是 .(2),(4)(2)三种方法可以相互转化它们之间有什么关系?3.你能将关系式法转化成图象法吗?什么是函数的图象?例1:画出下面正比例函数y=2x的图象.解:
xy100-12-2…………24-2-4关系式法列表法①列表典例精析y=2x②描点以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点③连线画函数图象的一般步骤:①列表②描点③连线根据这个步骤画出函数y=-3x的图象要点归纳这两个函数图象有什么共同特征?y1245-1-2-3-4-5-1-2-3-41430y=-3x32x125-1-2-3-4-5-1-2-3-41430-32xy=2x归纳总结由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.两点
作图法O用你认为最简单的方法画出下列函数的图象:
(1) y=-3x;(2)0-30y=-3x画一画例2 已知正比例函数y=(m+1)xm2 ,它的图象经过第几象限?m+1=2>0该函数是正比例函数∴根据正比例函数的性质,k>0可得该图象经过一、三象限.解:(1)若函数图象经过第一、三象限,则k的取值
范围是________.变式1: 已知正比例函数y=(k+1)x.k>-1(2)若函数图象经过点(2,4),则k_____.解析:因为函数图象经过第一、三象限,所以
k+1>0,解得k>-1.解析:将坐标(2,4)带入函数表达式中,得
4=(k+1)·2,解得k=1.=1变式2:当x>0时,y与x的函数解析式为y=2x ,
当x≤0时,y与x的函数解析为y=-2x ,则在同一直角
坐标系中的图象大致为( ) C画一画:在同一直角坐标系内画出正比例函数 y=x , y=3x, y=- x和 y=-4x 的图象. 这四个函数中,随着x的增大,y的值分别如何变化?当k>0时,x增大时,y的值也增大;当k<0时,x增大时,y的值反而减小.24 y = 2x 1224y随x的增大而增大y随x的增大而减小-3-6想一想:下列函数中,随着x的增大,y的值分别如何变化?在正比例函数y=kx中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.总结归纳(1)正比例函数y=x和y=3x中,随着x值的增大,y的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
(2)正比例函数y=- x和y=-4x中,随着x值的增大,y的值都减小了,其中哪一个减小得更快?你是如何判断的?|k|越大,直线越陡,直线越靠近y轴.练一练 1.已知正比例函数y=kx (k>0)的图象上有两点(x1,y1),
(x2,y2),若x1
C k1
又y的值随着x值的增大而减小,
所以m<0,故m=-2.正比例函数的图象和性质图象:经过原点的直线.
当k>0时,经过第一、三象限;
当k<0时,经过第二、四象限.性质:当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.画正比例函数图象的一般步骤:列表、描点、连线正比例函数 解析式 y =kx(k≠0) 性质:k>0,y 随x 的增大而增大;k<0,y 随 x 的增大而减小.一次函数解析式 y =kx+b(k≠0) 针对函数 y =kx+b,大家想研究什么?应该怎样研究? 在上一课的学习中,我们学会了正比例函数图象的画法,分为三个步骤.①列表②描点③连线 那么你能用同样的方法画出一次函数的图象吗? -3 -2 -154321 o-2-3-4-5 2 3 4 5xy 1y=-2x+1描点、
连线一次函数的图象
是什么?-1 列表例1:画出一次函数y=-2x+1的图象一次函数总结归纳一次函数y=kx+b的图象也称为直线y=kx+b. 一次函数y=kx+b的图象是一条直线,因此画一次函数图象时,只要确定两个点,再过这两点画直线就可以了.一般过
(0,b)和(1,k+b)或( ,0)O 用你认为最简单的方法画出下列函数的图象:
(1) y=-2x-1;(2) y=0.5x+1-1-31y=-2x-1做一做1.5y=0.5x+1也可以先画直线 y=-2x与 y=0.5x,再分别平移它们,也能得到直线y=-2x-1与 y=0.5x+1....xy2O...活动:请大家用描点法在同一坐标系内画出一次函数y=x+2,y=x-2的图象.0-31-42-23-140...y=x+2y=x-2思考:观察它们的图象有什么特点?y=xy=x+2y=x-2y2O●●观察三个函数图象的平移情况:探究归纳 把一次函数y=x+2,y=x-2的图象与y=x比较,发现:
1. 这三个函数的图象形状都是 ,并且倾斜程度
______.
2. 函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移
个单位长度而得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向____ 平移____个单位长度而得到.直线相同(0,2)上2(0,-2)下2 比较三个函数的解析式, 相同,
它们的图象的位置关系是 . 自变量系数k平行 一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).下上思考:与x轴的交点坐标是什么?要点归纳(1)将直线y=2x向上平移2个单位后所得图象对应的函数表达式为( )
A.y=2x-1 B.y=2x-2
C.y=2x+1 D.y=2x+2
(2)将正比例函数y=-6x的图象向上平移,则平移后所得图象对应的函数表达式可能是__________
(写出一个即可).练一练B y=-6x+3画一画1:在同一坐标系中作出下列函数的图象.(1)(2)(3)-3O-223123-1-1-2xy1思考:k,b的值跟图象有什么关系?画一画2: 在同一坐标系中作出下列函数的图象.(1)(2)(3)-3o-223123-1-1-2xy1思考:k,b的值跟图象有什么关系?在一次函数y=kx+b中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.由此得到一次函数性质:归纳总结例2 P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象
上的两点,下列判断中,正确的是( )A.y1>y2 C.当x1<x2时,y1<y2 B. y1<y2 D.当x1<x2时,y1>y2 D解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.提示:反过来也成立:y越大,x也越大.k 0,b 0>>k 0,b 0k 0,b 0k 0,b 0k 0,b 0k 0,b 0>>><<<<<==思考:根据一次函数的图象判断k,b的正负,并说出直线经过的象限:归纳总结 一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.① b>0时,直线经过 一、二、四象限;② b<0时,直线经过二、三、四象限.① b>0时,直线经过一、二、三象限; ② b<0时,直线经过一、三、四象限.两个一次函数y1=ax+b与y2=bx+a,它们在同一坐标系中的图象可能是( )练一练C 例3 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;解:(1)由题意得1-2m>0,解得(2)由题意得1-2m≠0且m-1<0,即(3)由题意得1-2m<0且m-1<0,解得一次函数函数的图象和性质当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.图象性质
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
