九年级下《第26章二次函数》单元检测试卷(含答案)
文档属性
| 名称 | 九年级下《第26章二次函数》单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-21 21:00:12 | ||
图片预览




文档简介
【专题突破训练】华师大版九年级数学下册 第26章 二次函数 单元检测试卷
一、单选题(共10题;共30分)
1.抛物线y=-2x2开口方向是(?? )
A.?向上?????????????????????????????????????B.?向下?????????????????????????????????????C.?向左?????????????????????????????????????D.?向右
2.二次函数y=x2-2x+3顶点坐标是(? ? )
A.?(-1,-2)?????????????????????????/B.?(1,2)?????????????????????????/C.?(-1,2)?????????????????????????/D.?(0,2)
3.已知抛物线y=
1
3
(x?4)2-3与y轴交点的坐标是( ? ? ? )
A.?(0,3)?????????????????????????B.?(0,-3)?????????????????????????C.?(0,
7
3
)?????????????????????????D.?(0, -
7
3
)
4.二次函数y= -2
x
2
+4x+1的图象如何移动就得到y=-2
x
2
的图象(?? ) A.?向左移动1个单位,向上移动3个单位??????????????????/B.?向右移动1个单位,向上移动3个单位 C.?向左移动1个单位,向下移动3个单位??????????????????/D.?向右移动1个单位,向下移动3个单位
5.在平面直角坐标系xOy中,将抛物线y=2x2 先向左平移1个单位长度,再向下平移3个单位长度后所得到的抛物线的解析式为 (???)
A.?y=2(x-1)2-3 ?????????????/B.?y=2(x-1)2+3?????????????/C.?y=2(x+1)2-3 ?????????????/D.?y=2(x+1)2+3
6.已知二次函数 ??=??
??
2
+????+?? 的图象如下图所示,则四个代数式 ?????? ,
??
2
?4???? , 2??+?? , ?????+?? 中,值为正数的有(?? )
/
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
7.如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是(?? ) /
A.?①③?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
8.已知一次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是(?? ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
9.如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是(?? )/
A.?b2>4ac?????????????????????????????????????????????????????????????/B.?ax2+bx+c≥-6 C.?若点(-2,m),(-5,n)在抛物线上,则m>n??????????/D.?关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1
10..如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2 , 此时M="0." 下列判断: ①当x>0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在; ④使得M=1的x值是?
1
2
或
2
2
.其中正确的是( ) /
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?③④
二、填空题(共10题;共30分)
11.若抛物线 ??=(???2)
??
2
的开口向上,则 ?? 的取值范围是________.
12.抛物线 ??=2
??
2
?1 的顶点坐标是________.
13.若A( ?
13
4
,
??
1
),B( ?
5
4
,
??
2
),C(1,
??
3
)为二次函数y=
??
2
+4x﹣5的图象上的三点,则
??
1
、
??
2
、
??
3
的大小关系是________.
14.抛物线与x轴交于点(1,0),(﹣3,0),则该抛物线可设为:________.
15.把二次函数y=﹣2x2+4x+3化成y=a(x﹣m)2+k的形式是________.
16.如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为________. /
17.将二次函数y=x2-2x化为y=(x-h)2+k的形式,结果为________
18.二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
19.若二次函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是________.
20.抛物线y=ax2+bx+c满足下列条件:(1)4a﹣b=0; (2)a﹣b+c>0;(3)与x轴有两个交点,且两交点的距离小于2.以下有四个结论:①a<0;②c>0;③ac= /b2;④ /<a< /.则其中正确结论的序号是________.
三、解答题(共9题;共60分)
21.如图,一块矩形草地的长为100m,宽为80m,欲在中间修筑两条互相垂直的宽为x(m)的小路,这时草坪的面积为y(m2).求y与x的函数关系式,并求出x的取值范围. /
22.已知抛物线C1:y1=2x2﹣4x+k与x轴只有一个公共点. (1)求k的值; (2)怎样平移抛物线C1就可以得到抛物线C2:y2=2(x+1)2﹣4k?请写出具体的平移方法; (3)若点A(1,t)和点B(m,n)都在抛物线C2:y2=2(x+1)2﹣4k上,且n<t,直接写出m的取值范围.
23.直线l:y=﹣
3
4
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
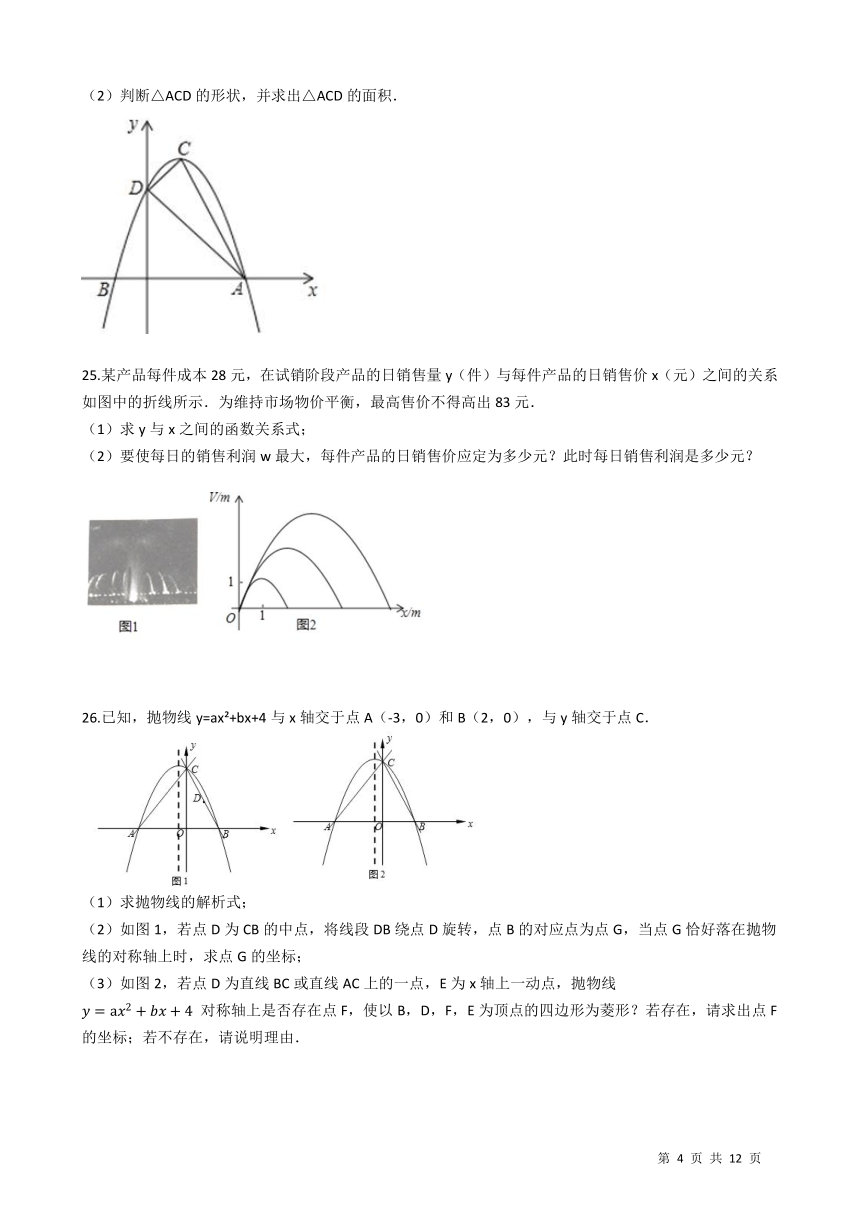
24.如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D. (1)求点B、点D的坐标, (2)判断△ACD的形状,并求出△ACD的面积. /
25.某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元. (1)求y与x之间的函数关系式; (2)要使每日的销售利润w最大,每件产品的日销售价应定为多少元?此时每日销售利润是多少元? /
26.已知,抛物线y=ax2+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C. /
(1)求抛物线的解析式;
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线 ??=a
??
2
+????+4 对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
27.如图,抛物线y=﹣x2﹣2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点. /
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=2
2
DQ,求点F的坐标.
28.甲、乙两人分别站在相距6米的A、B两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面1米的C处发出一球,乙在离地面1.5米的D处成功击球,球飞行过程中的最高点H与甲的水平距离AE为4米,现以A为原点,直线AB为x轴,建立平面直角坐标系(如图所示).求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度. /
29.已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM /
(1)画出△A1PM
(2)设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.
答案解析部分
一、单选题
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】A
7.【答案】D
8.【答案】C
9.【答案】C
10.【答案】D
二、填空题
11.【答案】a>2
12.【答案】(0,-1)
13.【答案】
??
2
<
??
1
<
??
3
14.【答案】y=a(x﹣1)(x+3)(a≠0)
15.【答案】y=﹣2(x﹣1)2+5
16.【答案】直线x=2
17.【答案】??=
(???1)
2
?1
18.【答案】
3
4
19.【答案】1
20.【答案】①
三、解答题
21.【答案】解:设中间修筑两条互相垂直的宽为x(m)的小路,草坪的面积为y(m2), 根据题意得出:y=100﹣80﹣80x﹣100x+x2=x2﹣180x+8000(0<x<80)
22.【答案】解:(1)根据题意得:△=16﹣8k=0,解得:k=2; (2)C1是:y1=2x2﹣4x+2=2(x﹣1)2 , 抛物线C2是:y2=2(x+1)2﹣8. 则平移抛物线C1就可以得到抛物线C2的方法是向左平移2个单位长度,向下平移8个单位长度; (3)当x=1时,y2=2(x+1)2﹣8=0,即t=0. 在y2=2(x+1)2﹣8中,令y=0,解得:x=1或﹣3. 则当n<t时,即2(x+1)2﹣8<0时,m的范围是﹣3<m<1.
23.【答案】解:∵y=﹣ /x+6交y轴于点A,与x轴交于点B, ∴x=0时,y=6, ∴A(0,6), y=0时,x=8, ∴B(8,0), ∵过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),BC=5, ∴C(3,0). 设抛物线m的解析式为y=a(x﹣3)(x﹣8), 将A(0,6)代入,得24a=6,解得a= /, ∴抛物线m的解析式为y= /(x﹣3)(x﹣8),即y= /x2﹣ /x+6; 函数图像如下: / 当抛物线m的函数值大于0时,x的取值范围是x<3或x>8.
24.【答案】解:(1)∵抛物线的顶点坐标为(1,4), ∴可设抛物线解析式为y=a(x﹣1)2+4, ∵与x轴交于点A(3,0), ∴0=4a+4,解得a=﹣1, ∴抛物线解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3, 令y=0,可得﹣x2+2x+3=0,解得x=﹣1或x=3,令x=0,可得y=3 ∴B点坐标为(﹣1,0),D点坐标为(0,3); (2)∵A(3,0),D(0,3),C(1,4), ∴AD=
3
2
+
3
2
=3
2
,CD=
1?0
2
+
4?3
2
=
2
,AC=
1?3
2
+
4?0
2
=2
5
, ∴AD2+CD2=(3
2
)2+(
2
)2=20=(2
5
)2=AC2 , ∴△ACD是以AC为斜边的直角三角形, ∴S△ACD=
1
2
AD?CD=
1
2
×3
2
×
2
=3.
25.【答案】解:(1)当30<x≤40时,设此段的函数解析式为:y=kx+b,
30??+??=66
40??+??=36
解得,k=﹣3,b=156 ∴当30<x≤40时,函数的解析式为:y=﹣3x+156; 当40<x≤80时,设此段函数的解析式为:y=mx+n,
40??+??=36
80??+??=16
解得,m=?
1
2
,n=56, ∴当40<x≤80时,函数的解析式为:y=?
1
2
??+56; 当80<x≤83时,y=16; 由上可得,y与x之间的函数关系式是:y=
?3??+15630?
1
2
??+56401680; (2)当30<x≤40时, w=(x﹣28)y =(x﹣28)(﹣3x+156) =﹣3x2+240x﹣4368 =﹣3(x﹣40)2+432 ∴当x=40时取得最大值,最大值为w=432元; 当40<x≤80时, w=(x﹣28)y =(x﹣28)(?
1
2
??+56) =?
1
2
??
2
+70?1586 =?
1
2
???70
2
+882, ∴当x=70时,取得最大值,最大值为w=882元; 当80<x≤83时,w=(x﹣28)×16 ∴当x=83时,取得最大值,最大值为w=880元; 由上可得,当x=70时,每日点的销售利润最大,最大为882元, 即要使每日的销售利润w最大,每件产品的日销售价应定为70元,此时每日销售利润是882元.
26.【答案】(1)由A(-3,0)和B(2,0),得: ??=??(??+3)(???2) ? ?????????? ??即 ??=??
??
2
+?????6?? = ax2+bx+4 ∴ ?6??=?4 ???????????????? ∴ ??=?
2
3
? ??????????????? ∴ ??=?
2
3
??
2
?
2
3
?????4 . (2)易得C(0,4),则BC=
4
2
+
2
2
=2
5
. 由 ??=?
2
3
??
2
?
2
3
?????4 可对称轴为x= ?
?
2
3
2×(?
2
3
)
=?
1
2
, 则可设点G的坐标为 (?
1
2
,??) , ∵点D是BC的中点 ∴点D的坐标为 (1,2) , ????=
1
2
????=
5
由旋转可得,DG=DB ∴
(1+
1
2
)
2
+
(???2)
2
=
(
5
)
2
…………… ∴ ??=2±
11
2
……… ∴点G的坐标为 (?
1
2
,2+
11
2
) 或 (?
1
2
,2?
11
2
) (3)①当BE为对角线时,因为菱形的对角线互相垂直平分,所以此时D即为对称轴与AC的交点或对称轴对BC的交点,F为点D关于x轴的对称点, 设
??
????
=????+?? , ∵C (0,4) ,A (?3,0) , ∴ {
??=4
?3??+??=0
, ∴ {
??=4
??=
4
3
, ∴
??
????
=
4
3
??+4 , ∴当 ??=?
1
2
时, ??=
10
3
, ∴D (?
1
2
,
10
3
) , ∴F (?
1
2
,?
10
3
) ; 易得
??
????
=?2??+4 ∴当 ??=?
1
2
时,y=5, ∴D (?
1
2
,5) , ∴F (?
1
2
,?5) ; ②当BE为菱形的边时,有DF∥BE I)当点D在直线BC上时
??
????
=?2??+4 设D (??,?2??+4) ,则点F (?
1
2
,?2??+4) ∵四边形BDFE是菱形 ∴FD=DB 根据勾股定理得, (??+
1
2
)
2
=
(???2)
2
+
(?2??+4)
2
整理得: 4
??
2
?21??+
79
4
=0, 解得:
??
1
=
21+5
5
8
,
??
2
=
21?5
5
8
∴F (?
1
2
,
?5?5
5
4
) 或 (?
1
2
,
?5+5
5
4
) II)当点D在直线AC上时 设D (?? ,
4
3
??+4) ,则点F (?
1
2
,
4
3
??+4) ∵四边形BFDE是菱形, ∴FD=FB , 根据勾股定理得,
(??+
1
2
)
2
=
(2+
1
2
)
2
+
(
4
3
??+4)
2
整理得: 7
??
2
+87??+198=0 , 解得:
??
1
=?3 (舍去),
??
2
=?
66
7
∴F (?
1
2
,?
60
7
) , 综上所述,点F的坐标分别为: (?
1
2
,?
10
3
) , (?
1
2
,?5) , (?
1
2
,
?5?5
5
4
) , (?
1
2
,
?5+5
5
4
) , (?
1
2
,?
60
7
) .
27.【答案】(1)解:当y=0时,﹣x2﹣2x+3=0,解得x1=1,x2=﹣3,则A(﹣3,0),B(1,0);当x=0时,y=﹣x2﹣2x+3=3,则C(0,3); (2)解:抛物线的对称轴为直线x=﹣1, 设M(x,0),则点P(x,﹣x2﹣2x+3),(﹣3<x<﹣1), ∵点P与点Q关于直线=﹣1对称, ∴点Q(﹣2﹣x,﹣x2﹣2x+3), ∴PQ=﹣2﹣x﹣x=﹣2﹣2x, ∴矩形PMNQ的周长=2(﹣2﹣2x﹣x2﹣2x+3)=﹣2x2﹣8x+2=﹣2(x+2)2+10, 当x=﹣2时,矩形PMNQ的周长最大,此时M(﹣2,0), 设直线AC的解析式为y=kx+b, 把A(﹣3,0),C(0,3)代入得 {
?3??+??=0
??=3
,解得 {
??=1
??=3
, ∴直线AC的解析式为y=3x+3, 当x=﹣2时,y=x+3=1, ∴E(﹣2,1), ∴△AEM的面积=
1
2
×(﹣2+3)×1=
1
2
; (3)解:当x=﹣2时,Q(0,3),即点C与点Q重合, 当x=﹣1时,y=﹣x2﹣2x+3=4,则D(﹣1,4), ∴DQ=
1
2
+
(3?4)
2
=
2
, ∴FG=2
2
DQ=2
2
×
2
=4, 设F(t,﹣t2﹣2t+3),则G(t,t+3), ∴GF=t+3﹣(﹣t2﹣2t+3)=t2+3t, ∴t2+3t=4,解得t1=﹣4,t2=1, ∴F点坐标为(﹣4,﹣5)或(1,0).
28.【答案】解:由题意得:C(0,1),D(6,1.5),抛物线的对称轴为直线x=4, 设抛物线的表达式为:y=ax2+bx+1(a≠0), 则据题意得: {
?
??
2??
=4
1.5=36??+6??+1
, 解得: {
??=?
1
24
??=
1
3
, ∴羽毛球飞行的路线所在的抛物线的表达式为:y=﹣
1
24
x2+
1
3
x+1, ∵y=﹣
1
24
(x﹣4)2+
5
3
, ∴飞行的最高高度为
5
3
米
29.【答案】(1)解:如图所示:△A1PM,即为所求; / (2)解:过点M作MD⊥AB于点D, ∵AB=BC=4,∠ABC=90°,M是AC的中点, ∴MD=2, 设AN=x,则BN=4﹣x, 故四边形NMCP的面积为: y=
1
2
×4×4﹣
1
2
x×2﹣
1
2
x×(4﹣x) =
1
2
x2﹣3x+8 =
1
2
(x﹣3)2+
7
2
, 故y的最小值为:
7
2
一、单选题(共10题;共30分)
1.抛物线y=-2x2开口方向是(?? )
A.?向上?????????????????????????????????????B.?向下?????????????????????????????????????C.?向左?????????????????????????????????????D.?向右
2.二次函数y=x2-2x+3顶点坐标是(? ? )
A.?(-1,-2)?????????????????????????/B.?(1,2)?????????????????????????/C.?(-1,2)?????????????????????????/D.?(0,2)
3.已知抛物线y=
1
3
(x?4)2-3与y轴交点的坐标是( ? ? ? )
A.?(0,3)?????????????????????????B.?(0,-3)?????????????????????????C.?(0,
7
3
)?????????????????????????D.?(0, -
7
3
)
4.二次函数y= -2
x
2
+4x+1的图象如何移动就得到y=-2
x
2
的图象(?? ) A.?向左移动1个单位,向上移动3个单位??????????????????/B.?向右移动1个单位,向上移动3个单位 C.?向左移动1个单位,向下移动3个单位??????????????????/D.?向右移动1个单位,向下移动3个单位
5.在平面直角坐标系xOy中,将抛物线y=2x2 先向左平移1个单位长度,再向下平移3个单位长度后所得到的抛物线的解析式为 (???)
A.?y=2(x-1)2-3 ?????????????/B.?y=2(x-1)2+3?????????????/C.?y=2(x+1)2-3 ?????????????/D.?y=2(x+1)2+3
6.已知二次函数 ??=??
??
2
+????+?? 的图象如下图所示,则四个代数式 ?????? ,
??
2
?4???? , 2??+?? , ?????+?? 中,值为正数的有(?? )
/
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
7.如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是(?? ) /
A.?①③?????????????????????????????????????B.?②③?????????????????????????????????????C.?②④?????????????????????????????????????D.?③④
8.已知一次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是(?? ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
9.如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是(?? )/
A.?b2>4ac?????????????????????????????????????????????????????????????/B.?ax2+bx+c≥-6 C.?若点(-2,m),(-5,n)在抛物线上,则m>n??????????/D.?关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1
10..如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2 , 此时M="0." 下列判断: ①当x>0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在; ④使得M=1的x值是?
1
2
或
2
2
.其中正确的是( ) /
A.?①②?????????????????????????????????????B.?①④?????????????????????????????????????C.?②③?????????????????????????????????????D.?③④
二、填空题(共10题;共30分)
11.若抛物线 ??=(???2)
??
2
的开口向上,则 ?? 的取值范围是________.
12.抛物线 ??=2
??
2
?1 的顶点坐标是________.
13.若A( ?
13
4
,
??
1
),B( ?
5
4
,
??
2
),C(1,
??
3
)为二次函数y=
??
2
+4x﹣5的图象上的三点,则
??
1
、
??
2
、
??
3
的大小关系是________.
14.抛物线与x轴交于点(1,0),(﹣3,0),则该抛物线可设为:________.
15.把二次函数y=﹣2x2+4x+3化成y=a(x﹣m)2+k的形式是________.
16.如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,则它的对称轴为________. /
17.将二次函数y=x2-2x化为y=(x-h)2+k的形式,结果为________
18.二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
19.若二次函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是________.
20.抛物线y=ax2+bx+c满足下列条件:(1)4a﹣b=0; (2)a﹣b+c>0;(3)与x轴有两个交点,且两交点的距离小于2.以下有四个结论:①a<0;②c>0;③ac= /b2;④ /<a< /.则其中正确结论的序号是________.
三、解答题(共9题;共60分)
21.如图,一块矩形草地的长为100m,宽为80m,欲在中间修筑两条互相垂直的宽为x(m)的小路,这时草坪的面积为y(m2).求y与x的函数关系式,并求出x的取值范围. /
22.已知抛物线C1:y1=2x2﹣4x+k与x轴只有一个公共点. (1)求k的值; (2)怎样平移抛物线C1就可以得到抛物线C2:y2=2(x+1)2﹣4k?请写出具体的平移方法; (3)若点A(1,t)和点B(m,n)都在抛物线C2:y2=2(x+1)2﹣4k上,且n<t,直接写出m的取值范围.
23.直线l:y=﹣
3
4
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
24.如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),B两点,交y轴于点D. (1)求点B、点D的坐标, (2)判断△ACD的形状,并求出△ACD的面积. /
25.某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元. (1)求y与x之间的函数关系式; (2)要使每日的销售利润w最大,每件产品的日销售价应定为多少元?此时每日销售利润是多少元? /
26.已知,抛物线y=ax2+bx+4与x轴交于点A(-3,0)和B(2,0),与y轴交于点C. /
(1)求抛物线的解析式;
(2)如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
(3)如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线 ??=a
??
2
+????+4 对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.
27.如图,抛物线y=﹣x2﹣2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点. /
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=2
2
DQ,求点F的坐标.
28.甲、乙两人分别站在相距6米的A、B两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面1米的C处发出一球,乙在离地面1.5米的D处成功击球,球飞行过程中的最高点H与甲的水平距离AE为4米,现以A为原点,直线AB为x轴,建立平面直角坐标系(如图所示).求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度. /
29.已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM /
(1)画出△A1PM
(2)设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.
答案解析部分
一、单选题
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】A
7.【答案】D
8.【答案】C
9.【答案】C
10.【答案】D
二、填空题
11.【答案】a>2
12.【答案】(0,-1)
13.【答案】
??
2
<
??
1
<
??
3
14.【答案】y=a(x﹣1)(x+3)(a≠0)
15.【答案】y=﹣2(x﹣1)2+5
16.【答案】直线x=2
17.【答案】??=
(???1)
2
?1
18.【答案】
3
4
19.【答案】1
20.【答案】①
三、解答题
21.【答案】解:设中间修筑两条互相垂直的宽为x(m)的小路,草坪的面积为y(m2), 根据题意得出:y=100﹣80﹣80x﹣100x+x2=x2﹣180x+8000(0<x<80)
22.【答案】解:(1)根据题意得:△=16﹣8k=0,解得:k=2; (2)C1是:y1=2x2﹣4x+2=2(x﹣1)2 , 抛物线C2是:y2=2(x+1)2﹣8. 则平移抛物线C1就可以得到抛物线C2的方法是向左平移2个单位长度,向下平移8个单位长度; (3)当x=1时,y2=2(x+1)2﹣8=0,即t=0. 在y2=2(x+1)2﹣8中,令y=0,解得:x=1或﹣3. 则当n<t时,即2(x+1)2﹣8<0时,m的范围是﹣3<m<1.
23.【答案】解:∵y=﹣ /x+6交y轴于点A,与x轴交于点B, ∴x=0时,y=6, ∴A(0,6), y=0时,x=8, ∴B(8,0), ∵过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),BC=5, ∴C(3,0). 设抛物线m的解析式为y=a(x﹣3)(x﹣8), 将A(0,6)代入,得24a=6,解得a= /, ∴抛物线m的解析式为y= /(x﹣3)(x﹣8),即y= /x2﹣ /x+6; 函数图像如下: / 当抛物线m的函数值大于0时,x的取值范围是x<3或x>8.
24.【答案】解:(1)∵抛物线的顶点坐标为(1,4), ∴可设抛物线解析式为y=a(x﹣1)2+4, ∵与x轴交于点A(3,0), ∴0=4a+4,解得a=﹣1, ∴抛物线解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3, 令y=0,可得﹣x2+2x+3=0,解得x=﹣1或x=3,令x=0,可得y=3 ∴B点坐标为(﹣1,0),D点坐标为(0,3); (2)∵A(3,0),D(0,3),C(1,4), ∴AD=
3
2
+
3
2
=3
2
,CD=
1?0
2
+
4?3
2
=
2
,AC=
1?3
2
+
4?0
2
=2
5
, ∴AD2+CD2=(3
2
)2+(
2
)2=20=(2
5
)2=AC2 , ∴△ACD是以AC为斜边的直角三角形, ∴S△ACD=
1
2
AD?CD=
1
2
×3
2
×
2
=3.
25.【答案】解:(1)当30<x≤40时,设此段的函数解析式为:y=kx+b,
30??+??=66
40??+??=36
解得,k=﹣3,b=156 ∴当30<x≤40时,函数的解析式为:y=﹣3x+156; 当40<x≤80时,设此段函数的解析式为:y=mx+n,
40??+??=36
80??+??=16
解得,m=?
1
2
,n=56, ∴当40<x≤80时,函数的解析式为:y=?
1
2
??+56; 当80<x≤83时,y=16; 由上可得,y与x之间的函数关系式是:y=
?3??+15630?
1
2
??+56401680; (2)当30<x≤40时, w=(x﹣28)y =(x﹣28)(﹣3x+156) =﹣3x2+240x﹣4368 =﹣3(x﹣40)2+432 ∴当x=40时取得最大值,最大值为w=432元; 当40<x≤80时, w=(x﹣28)y =(x﹣28)(?
1
2
??+56) =?
1
2
??
2
+70?1586 =?
1
2
???70
2
+882, ∴当x=70时,取得最大值,最大值为w=882元; 当80<x≤83时,w=(x﹣28)×16 ∴当x=83时,取得最大值,最大值为w=880元; 由上可得,当x=70时,每日点的销售利润最大,最大为882元, 即要使每日的销售利润w最大,每件产品的日销售价应定为70元,此时每日销售利润是882元.
26.【答案】(1)由A(-3,0)和B(2,0),得: ??=??(??+3)(???2) ? ?????????? ??即 ??=??
??
2
+?????6?? = ax2+bx+4 ∴ ?6??=?4 ???????????????? ∴ ??=?
2
3
? ??????????????? ∴ ??=?
2
3
??
2
?
2
3
?????4 . (2)易得C(0,4),则BC=
4
2
+
2
2
=2
5
. 由 ??=?
2
3
??
2
?
2
3
?????4 可对称轴为x= ?
?
2
3
2×(?
2
3
)
=?
1
2
, 则可设点G的坐标为 (?
1
2
,??) , ∵点D是BC的中点 ∴点D的坐标为 (1,2) , ????=
1
2
????=
5
由旋转可得,DG=DB ∴
(1+
1
2
)
2
+
(???2)
2
=
(
5
)
2
…………… ∴ ??=2±
11
2
……… ∴点G的坐标为 (?
1
2
,2+
11
2
) 或 (?
1
2
,2?
11
2
) (3)①当BE为对角线时,因为菱形的对角线互相垂直平分,所以此时D即为对称轴与AC的交点或对称轴对BC的交点,F为点D关于x轴的对称点, 设
??
????
=????+?? , ∵C (0,4) ,A (?3,0) , ∴ {
??=4
?3??+??=0
, ∴ {
??=4
??=
4
3
, ∴
??
????
=
4
3
??+4 , ∴当 ??=?
1
2
时, ??=
10
3
, ∴D (?
1
2
,
10
3
) , ∴F (?
1
2
,?
10
3
) ; 易得
??
????
=?2??+4 ∴当 ??=?
1
2
时,y=5, ∴D (?
1
2
,5) , ∴F (?
1
2
,?5) ; ②当BE为菱形的边时,有DF∥BE I)当点D在直线BC上时
??
????
=?2??+4 设D (??,?2??+4) ,则点F (?
1
2
,?2??+4) ∵四边形BDFE是菱形 ∴FD=DB 根据勾股定理得, (??+
1
2
)
2
=
(???2)
2
+
(?2??+4)
2
整理得: 4
??
2
?21??+
79
4
=0, 解得:
??
1
=
21+5
5
8
,
??
2
=
21?5
5
8
∴F (?
1
2
,
?5?5
5
4
) 或 (?
1
2
,
?5+5
5
4
) II)当点D在直线AC上时 设D (?? ,
4
3
??+4) ,则点F (?
1
2
,
4
3
??+4) ∵四边形BFDE是菱形, ∴FD=FB , 根据勾股定理得,
(??+
1
2
)
2
=
(2+
1
2
)
2
+
(
4
3
??+4)
2
整理得: 7
??
2
+87??+198=0 , 解得:
??
1
=?3 (舍去),
??
2
=?
66
7
∴F (?
1
2
,?
60
7
) , 综上所述,点F的坐标分别为: (?
1
2
,?
10
3
) , (?
1
2
,?5) , (?
1
2
,
?5?5
5
4
) , (?
1
2
,
?5+5
5
4
) , (?
1
2
,?
60
7
) .
27.【答案】(1)解:当y=0时,﹣x2﹣2x+3=0,解得x1=1,x2=﹣3,则A(﹣3,0),B(1,0);当x=0时,y=﹣x2﹣2x+3=3,则C(0,3); (2)解:抛物线的对称轴为直线x=﹣1, 设M(x,0),则点P(x,﹣x2﹣2x+3),(﹣3<x<﹣1), ∵点P与点Q关于直线=﹣1对称, ∴点Q(﹣2﹣x,﹣x2﹣2x+3), ∴PQ=﹣2﹣x﹣x=﹣2﹣2x, ∴矩形PMNQ的周长=2(﹣2﹣2x﹣x2﹣2x+3)=﹣2x2﹣8x+2=﹣2(x+2)2+10, 当x=﹣2时,矩形PMNQ的周长最大,此时M(﹣2,0), 设直线AC的解析式为y=kx+b, 把A(﹣3,0),C(0,3)代入得 {
?3??+??=0
??=3
,解得 {
??=1
??=3
, ∴直线AC的解析式为y=3x+3, 当x=﹣2时,y=x+3=1, ∴E(﹣2,1), ∴△AEM的面积=
1
2
×(﹣2+3)×1=
1
2
; (3)解:当x=﹣2时,Q(0,3),即点C与点Q重合, 当x=﹣1时,y=﹣x2﹣2x+3=4,则D(﹣1,4), ∴DQ=
1
2
+
(3?4)
2
=
2
, ∴FG=2
2
DQ=2
2
×
2
=4, 设F(t,﹣t2﹣2t+3),则G(t,t+3), ∴GF=t+3﹣(﹣t2﹣2t+3)=t2+3t, ∴t2+3t=4,解得t1=﹣4,t2=1, ∴F点坐标为(﹣4,﹣5)或(1,0).
28.【答案】解:由题意得:C(0,1),D(6,1.5),抛物线的对称轴为直线x=4, 设抛物线的表达式为:y=ax2+bx+1(a≠0), 则据题意得: {
?
??
2??
=4
1.5=36??+6??+1
, 解得: {
??=?
1
24
??=
1
3
, ∴羽毛球飞行的路线所在的抛物线的表达式为:y=﹣
1
24
x2+
1
3
x+1, ∵y=﹣
1
24
(x﹣4)2+
5
3
, ∴飞行的最高高度为
5
3
米
29.【答案】(1)解:如图所示:△A1PM,即为所求; / (2)解:过点M作MD⊥AB于点D, ∵AB=BC=4,∠ABC=90°,M是AC的中点, ∴MD=2, 设AN=x,则BN=4﹣x, 故四边形NMCP的面积为: y=
1
2
×4×4﹣
1
2
x×2﹣
1
2
x×(4﹣x) =
1
2
x2﹣3x+8 =
1
2
(x﹣3)2+
7
2
, 故y的最小值为:
7
2
