湘教版九年级上《第五章用样本推断总体》单元检测试卷(含答案)
文档属性
| 名称 | 湘教版九年级上《第五章用样本推断总体》单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 398.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-21 21:02:19 | ||
图片预览


文档简介
【专题突破训练】湘教版九年级数学上册 第五章 用样本推断总体 单元检测试卷
一、单选题(共10题;共30分)
1.(2017?德州)某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
尺码
39
40
41
42
43
平均每天销售数量/件
10
12
20
12
12
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是(?? )
A.?平均数??????????????????????????????????/B.?方差??????????????????????????????????/C.?众数??????????????????????????????????/D.?中位数
2.下列说法,错误的是(?? )
A.?为了解一种灯泡的使用寿命,宜采用普查的方法 B.?众数在一组数据中若存在,可以不唯一 C.?方差反映了一组数据与其平均数的偏离程度 D.?对于简单随机样本,可以用样本的方差去估计总体的方差
3.某一段时间,小芳测得连续五天的日最高气温后,整理得出下表(有两个数据被遮盖). / 被遮盖的两个数据依次是(???)
A.?3℃,2;???????????????????????????B.?3℃,4;???????????????????????????C.?4℃,2;???????????????????????????D.?4℃,4.
4.某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课
A
B
C
D
E
F
人数
20
30
?
根据图标提供的信息,下列结论错误的是(?? ) /
A.?这次被调查的学生人数为200人??????????????????????????/B.?扇形统计图中E部分扇形的圆心角为72° C.?被调查的学生中最想选F的人数为35人????????????????/D.?被调查的学生中最想选D的有55人
5.某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:
尺码(cm)
23.5
24
24.5
25
25.5
销售量(双)
1
2
2
5
1
则这11双鞋的尺码组成的一组数据中,众数和中位数分别是(????)
A.?25,25???????????????????????????B.?24.5,25???????????????????????????C.?25,24.5???????????????????????????D.?24.5,24.5
6.甲、乙两班举行班际电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表: / 通过计算可知两组数据的方差分别为S2甲=2.0,S2乙=2.7,则下列说法:①两组数据的平均数相同;②甲组学生比乙组学生的成绩稳定;③两组学生成绩的中位数相同;④两组学生成绩的众数相同。其中正确的有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
7.为了解某市初中生视力情况,有关部门进行了一次抽样调查,数据如下表,若该市共有初中生15万人,则全市视力不良的初中生的人数大约是( ??) /
A.?2160人??????????????????????????????/B.?7.2万人??????????????????????????????/C.?7.8万人??????????????????????????????/D.?4500人
8.为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是(?? ) /
A.?12?????????????????????????????????????????/B.?12.5?????????????????????????????????????????/C.?13?????????????????????????????????????????/D.?14
9.某中学足球队的18名队员的年龄情况如下表: / 则这些队员年龄的众数和中位数分别是( )
A.?15,15?????????????????????????????/B.?15,15.5?????????????????????????????/C.?15,16?????????????????????????????/D.?16,15
10.某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9,利用上述数据估计该小区2 000户家庭一周内需要环保方便袋(??? )只.
A.?2000?????????????????????????????????/B.?14000?????????????????????????????????/C.?28000?????????????????????????????????/D.?98000
二、填空题(共10题;共30分)
11.某中学为了了解学生上学方式,现随机抽取部分学生进行调查,将结果绘成条形统计图如图,由此可估计该校2400名学生中有________名学生是乘车上学的. /
12.我市少体校为了从甲、乙两名运动员中选出一名运动员参加省运动会百米比赛,组织了选拔测试,分别对两人进行了五次测试,成绩(单位:秒)以及平均数、方差如表:
甲
13
13
14
16
18
??
甲
?
=14.8
??
甲
2
=3.76
乙
14
14
15
15
16
??
乙
?
=14.8
??
乙
2
=0.56
学校决定派乙运动员参加比赛,理由是________.
13.彭山的枇杷大又甜,在今年5月18日“彭山枇杷节”期间,从山上5棵枇杷树上采摘到了200千克枇杷,请估计彭山近600棵枇杷树今年一共收获了枇杷________千克.
14.甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为
??
甲
2
=16.7,乙比赛成绩的方差为
??
乙
2
=28.3,那么成绩比较稳定的是________(填“甲”或“乙”).
15.某校九年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表:
班级
参加人数
平均字数
中位数
方差
甲
55
135
149
191
乙
55
135
151
110
有一位同学根据上面表格得出如下结论:①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大. 上述结论正确的是________(填序号).
16.如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有________人. /
17.某养鱼专业户为了估计鱼塘中鱼的总条数,他先从鱼塘中捞出100条,将每条鱼作了记号后放回水中,当它们完全混合于鱼群后,再从鱼塘中捞出100条鱼,发现其中带记号的鱼有10条,估计该鱼塘里约有________?条鱼.
18.某学校共有学生3000人,为了解学生的课外阅读情况,随机调查了200名同学,其中120人有阅读课外书的习惯,则该学校大约________人有阅读课外书的习惯.
19.某人走进一家商店,进门付l角钱,然后在店里购物花掉当时他手中钱的一半,走出商店付1角钱;之后,他走进第二家商店付1角钱,在店里花掉当时他手中钱的一半, 走出商店付1角钱;他又进第三家商店付l角钱,在店里花掉当时他手中钱的一半,出店付1角钱;最后他走进第四家商店付l角钱,在店里花掉当时他手中钱的一半, 出店付1角钱,这时他一分钱也没有了.该人原有钱的数目是________角.
20.为了解某校师生捐书情况,随机调查了部分师生,根据调查结果绘制了如图所示的统计图.若该校共有师生1000人,则捐文学类书籍的师生约有________人. /
三、解答题(共10题;共60分)
21.一个水库养了某种鱼,从中捕捞了20条,称得它们的重量如下:(单位:千克)1.15、1.04、1.11、1.07、1.10、1.32、1.25、1.19、1.15、1.21、1.18、1.14、1.09、1.25、1.21、1.29、1.16、1.24、1.12、1.16,那么这组数据的平均数是多少?我们能否据此估计水库中鱼的平均重量?
22.某农场学校积极开展阳光体育活动,组织了八年级学生定点投篮,规定每人投篮3次.现对八年级(5)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题. (1)求出八年级(5)班学生人数; (2)补全两个统计图; (3)求出扇形统计图中3次的圆心角的度数; (4)若八年级有学生200人,估计投中次数在2次以上(包括2次)的人数. /
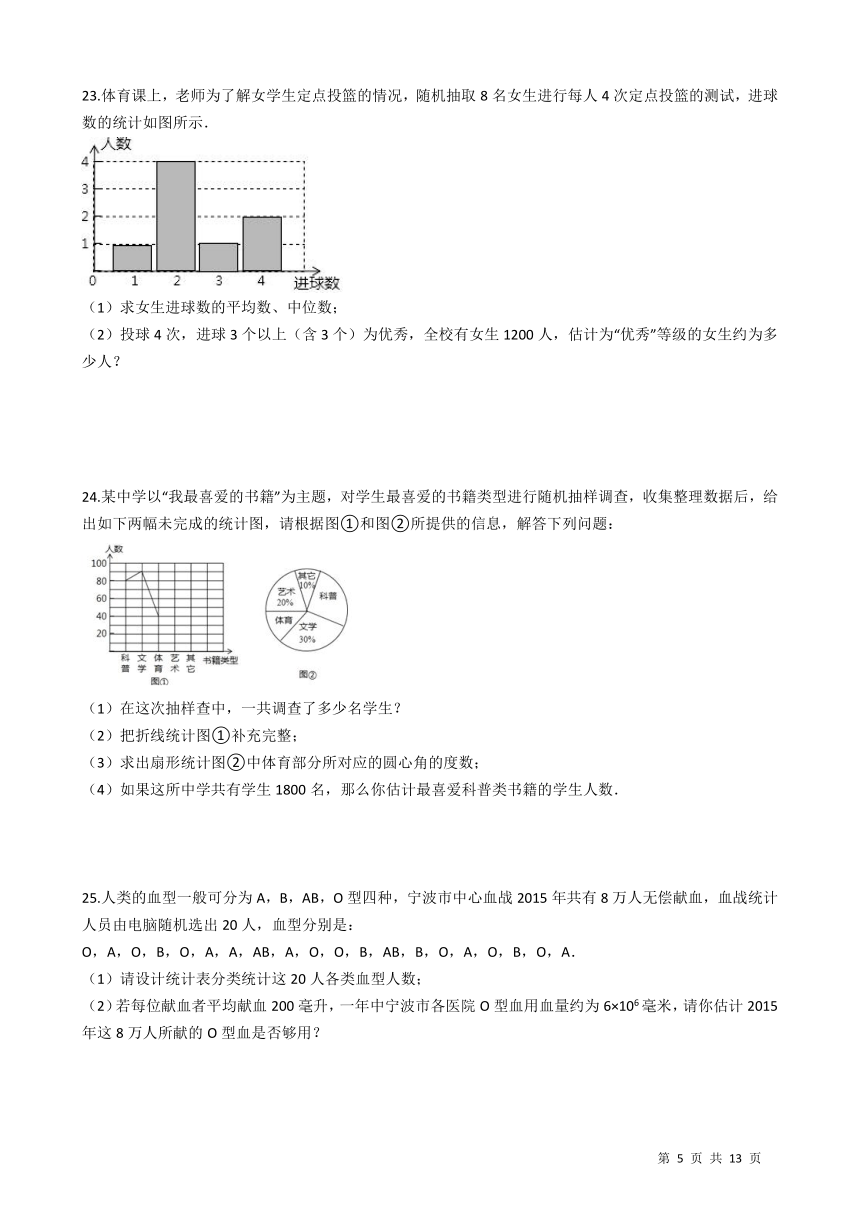
23.体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示. /
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
24.某中学以“我最喜爱的书籍”为主题,对学生最喜爱的书籍类型进行随机抽样调查,收集整理数据后,给出如下两幅未完成的统计图,请根据图①和图②所提供的信息,解答下列问题: / (1)在这次抽样查中,一共调查了多少名学生? (2)把折线统计图①补充完整; (3)求出扇形统计图②中体育部分所对应的圆心角的度数; (4)如果这所中学共有学生1800名,那么你估计最喜爱科普类书籍的学生人数.
25.人类的血型一般可分为A,B,AB,O型四种,宁波市中心血战2015年共有8万人无偿献血,血战统计人员由电脑随机选出20人,血型分别是: O,A,O,B,O,A,A,AB,A,O,O,B,AB,B,O,A,O,B,O,A. (1)请设计统计表分类统计这20人各类血型人数; (2)若每位献血者平均献血200毫升,一年中宁波市各医院O型血用血量约为6×106毫米,请你估计2015年这8万人所献的O型血是否够用?
26. (本题8分)某校为了解学生体质情况,从各年级学生中随机抽取部分学生进行体能测试. 每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制 成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题: / /
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
27.某中学开展“阳光体育一小时”活动.根据学校事假情况,决定开设四项运动项目:A:踢毽子;B:篮球;C:跳绳;D:乒乓球.为了解学生最喜欢哪一种运动项目,随机抽取了n名学生进行问卷调查,每位学生在问卷调查时都按要求只选择了其中一种喜欢的运动项目.收回全部问卷后,将收集到的数据整理并绘制成如下的统计图,若参与调查的学生中喜欢A方式的学生的人数占参与调查学生人数的40%.根据统计图提供的信息,解答下列问题: (1)求n的值. (2)求参与调查的学生中喜欢C的学生的人数. (3)根据统计结果,估计该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数. /
28.某班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况,八年级300名同学零花钱的最主要用途情况,九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据. /
时间
1小时左右
1.5小时左右
2小时左右
2.5小时左右
人数
50
80
120
50
根据以上信息,请回答下列问题: (1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少; (2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图; (3)九年级300名同学中完成家庭作业的平均时间大约是多少小时?(结果保留一位小数)
29.某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画.要求每位同学必须参加,且限报一项活动.以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图.请你结合图示所给出的信息解答下列问题.
?/
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
30.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某 食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A、B、C、D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图. 请根据以上信息回答: / ⑴本次参加抽样调查的居民有多少人? ⑵将不完整的条形图补充完整. ⑶若居民区有8000人,请估计爱吃D粽的人数? ⑷若有外型完全相同的A、B、C、D粽各一个煮熟后,小王吃了俩个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率?
答案解析部分
一、单选题
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】B
10.【答案】B
二、填空题
11.【答案】312
12.【答案】虽然甲、乙两名运动员的平均成绩相同,但乙运动员的成绩的方差较小,成绩稳定
13.【答案】24000
14.【答案】甲
15.【答案】①②③
16.【答案】400
17.【答案】1000
18.【答案】1800.
19.【答案】45
20.【答案】350
三、解答题
21.【答案】这组数据的平均数=(1.15+1.04+…+1.16)÷20=1.172(千克).能估计水库中鱼的平均重量,估计水库中鱼的平均重量为1.172千克
22.【答案】解:(1)八年级(5)班学生人数:2÷5%=40(人); (2)投中两次的人数:40-2-12-8=18(人), 18÷40×100%=45%,8÷40×100%=20%. 如图所示: / (3)360°×20%=72°; (4)200×(1-5%-30%)=130(人), 答:投中次数在2次以上(包括2次)的人数有130人.
23.【答案】(1)解:由条形统计图可得,女生进球数的平均数为:(1×1+2×4+1×3+4×2)÷8=2.5(个); ∵第4,5个数据都是2,则其平均数为:2; ∴女生进球数的中位数为:2 (2)解:样本中优秀率为:
3
8
, 故全校有女生1200人,“优秀”等级的女生为:1200×
3
8
=450(人), 答:“优秀”等级的女生约为450人
24.【答案】解:(1)90÷30%=300(名), 故一共调查了300名学生; (2)艺术的人数:300×20%=60(名), 其它的人数:300×10%=30(名); 补全折线图如图: / (3)体育部分所对应的圆心角的度数为:
40
300
×360°=48°; (4)1800×
80
300
=480(名).
25.【答案】解:(1)统计表格如图: / (2)
8
20
×8×
10
4
×200=6.4×
10
6
, 6.4×106>6×106 , 答:O型血够用.
26.【答案】(1)解:填写的统计表如图1所示: / (2)解:补全的条形统计图如图2所示: / (3)解:抽取的学生中体能测试的优秀率为:12÷50=24%; ∴该校体能测试为“优秀”的人数为1500×24%=360(人)
27.【答案】解:(1)80÷40%=200(人); (2)200﹣80﹣30﹣50=40(人); (3)
40?30
200
×1800=90(人), 答:该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多90人.
28.【答案】解:(1)冰红茶的百分比为100%﹣25%﹣25%﹣10%=40%,冰红茶的人数为400×40%=160(人), 即七年级同学最喜欢喝“冰红茶”的人数是160人; (2)补全频数分布直方图如右图所示. (3)
1×50+1.5×80+2×120+2.5×50
50+80+120+50
(小时). 答:九年级300名同学完成家庭作业的平均时间约为1.8小时. ?/
29.【答案】解:(1)学生的总数是:
20
40%
×100%=50(人),
参加书法比赛的学生所占的比例是:
10
50
×100%=20%,
则参加绘画比赛的学生所占的比例是:1﹣28%﹣40%﹣20%=12%,
(2)参加书法比赛的学生所占的比例是20%,
则扇形的圆心角的度数是:360×20%=72°;
(3)参加演讲比赛的人数是:600×28%=168(人),
参加唱歌比赛的人数是:600×40%=240(人).
30.【答案】解:(1)60÷10%=600(人). 答:本次参加抽样调查的居民有600人. (2)如图; / (3)8000×40%=3200(人). 答:该居民区有8000人,估计爱吃D粽的人有3200人。 (4)如图; / P(C粽)=
3
12
=
1
4
. 答:他第二个吃到的恰好是C粽的概率是
1
4
.
一、单选题(共10题;共30分)
1.(2017?德州)某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
尺码
39
40
41
42
43
平均每天销售数量/件
10
12
20
12
12
该店主决定本周进货时,增加了一些41码的衬衫,影响该店主决策的统计量是(?? )
A.?平均数??????????????????????????????????/B.?方差??????????????????????????????????/C.?众数??????????????????????????????????/D.?中位数
2.下列说法,错误的是(?? )
A.?为了解一种灯泡的使用寿命,宜采用普查的方法 B.?众数在一组数据中若存在,可以不唯一 C.?方差反映了一组数据与其平均数的偏离程度 D.?对于简单随机样本,可以用样本的方差去估计总体的方差
3.某一段时间,小芳测得连续五天的日最高气温后,整理得出下表(有两个数据被遮盖). / 被遮盖的两个数据依次是(???)
A.?3℃,2;???????????????????????????B.?3℃,4;???????????????????????????C.?4℃,2;???????????????????????????D.?4℃,4.
4.某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课
A
B
C
D
E
F
人数
20
30
?
根据图标提供的信息,下列结论错误的是(?? ) /
A.?这次被调查的学生人数为200人??????????????????????????/B.?扇形统计图中E部分扇形的圆心角为72° C.?被调查的学生中最想选F的人数为35人????????????????/D.?被调查的学生中最想选D的有55人
5.某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:
尺码(cm)
23.5
24
24.5
25
25.5
销售量(双)
1
2
2
5
1
则这11双鞋的尺码组成的一组数据中,众数和中位数分别是(????)
A.?25,25???????????????????????????B.?24.5,25???????????????????????????C.?25,24.5???????????????????????????D.?24.5,24.5
6.甲、乙两班举行班际电脑汉字输入比赛,各选10名选手参赛,各班参赛学生每分钟输入汉字个数统计如下表: / 通过计算可知两组数据的方差分别为S2甲=2.0,S2乙=2.7,则下列说法:①两组数据的平均数相同;②甲组学生比乙组学生的成绩稳定;③两组学生成绩的中位数相同;④两组学生成绩的众数相同。其中正确的有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
7.为了解某市初中生视力情况,有关部门进行了一次抽样调查,数据如下表,若该市共有初中生15万人,则全市视力不良的初中生的人数大约是( ??) /
A.?2160人??????????????????????????????/B.?7.2万人??????????????????????????????/C.?7.8万人??????????????????????????????/D.?4500人
8.为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了60株黄瓜,并可估计出这个新品种黄瓜平均每株结出的黄瓜根数是(?? ) /
A.?12?????????????????????????????????????????/B.?12.5?????????????????????????????????????????/C.?13?????????????????????????????????????????/D.?14
9.某中学足球队的18名队员的年龄情况如下表: / 则这些队员年龄的众数和中位数分别是( )
A.?15,15?????????????????????????????/B.?15,15.5?????????????????????????????/C.?15,16?????????????????????????????/D.?16,15
10.某“中学生暑期环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9,利用上述数据估计该小区2 000户家庭一周内需要环保方便袋(??? )只.
A.?2000?????????????????????????????????/B.?14000?????????????????????????????????/C.?28000?????????????????????????????????/D.?98000
二、填空题(共10题;共30分)
11.某中学为了了解学生上学方式,现随机抽取部分学生进行调查,将结果绘成条形统计图如图,由此可估计该校2400名学生中有________名学生是乘车上学的. /
12.我市少体校为了从甲、乙两名运动员中选出一名运动员参加省运动会百米比赛,组织了选拔测试,分别对两人进行了五次测试,成绩(单位:秒)以及平均数、方差如表:
甲
13
13
14
16
18
??
甲
?
=14.8
??
甲
2
=3.76
乙
14
14
15
15
16
??
乙
?
=14.8
??
乙
2
=0.56
学校决定派乙运动员参加比赛,理由是________.
13.彭山的枇杷大又甜,在今年5月18日“彭山枇杷节”期间,从山上5棵枇杷树上采摘到了200千克枇杷,请估计彭山近600棵枇杷树今年一共收获了枇杷________千克.
14.甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为
??
甲
2
=16.7,乙比赛成绩的方差为
??
乙
2
=28.3,那么成绩比较稳定的是________(填“甲”或“乙”).
15.某校九年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表:
班级
参加人数
平均字数
中位数
方差
甲
55
135
149
191
乙
55
135
151
110
有一位同学根据上面表格得出如下结论:①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大. 上述结论正确的是________(填序号).
16.如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生1000人,则根据此估计步行上学的有________人. /
17.某养鱼专业户为了估计鱼塘中鱼的总条数,他先从鱼塘中捞出100条,将每条鱼作了记号后放回水中,当它们完全混合于鱼群后,再从鱼塘中捞出100条鱼,发现其中带记号的鱼有10条,估计该鱼塘里约有________?条鱼.
18.某学校共有学生3000人,为了解学生的课外阅读情况,随机调查了200名同学,其中120人有阅读课外书的习惯,则该学校大约________人有阅读课外书的习惯.
19.某人走进一家商店,进门付l角钱,然后在店里购物花掉当时他手中钱的一半,走出商店付1角钱;之后,他走进第二家商店付1角钱,在店里花掉当时他手中钱的一半, 走出商店付1角钱;他又进第三家商店付l角钱,在店里花掉当时他手中钱的一半,出店付1角钱;最后他走进第四家商店付l角钱,在店里花掉当时他手中钱的一半, 出店付1角钱,这时他一分钱也没有了.该人原有钱的数目是________角.
20.为了解某校师生捐书情况,随机调查了部分师生,根据调查结果绘制了如图所示的统计图.若该校共有师生1000人,则捐文学类书籍的师生约有________人. /
三、解答题(共10题;共60分)
21.一个水库养了某种鱼,从中捕捞了20条,称得它们的重量如下:(单位:千克)1.15、1.04、1.11、1.07、1.10、1.32、1.25、1.19、1.15、1.21、1.18、1.14、1.09、1.25、1.21、1.29、1.16、1.24、1.12、1.16,那么这组数据的平均数是多少?我们能否据此估计水库中鱼的平均重量?
22.某农场学校积极开展阳光体育活动,组织了八年级学生定点投篮,规定每人投篮3次.现对八年级(5)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题. (1)求出八年级(5)班学生人数; (2)补全两个统计图; (3)求出扇形统计图中3次的圆心角的度数; (4)若八年级有学生200人,估计投中次数在2次以上(包括2次)的人数. /
23.体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示. /
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
24.某中学以“我最喜爱的书籍”为主题,对学生最喜爱的书籍类型进行随机抽样调查,收集整理数据后,给出如下两幅未完成的统计图,请根据图①和图②所提供的信息,解答下列问题: / (1)在这次抽样查中,一共调查了多少名学生? (2)把折线统计图①补充完整; (3)求出扇形统计图②中体育部分所对应的圆心角的度数; (4)如果这所中学共有学生1800名,那么你估计最喜爱科普类书籍的学生人数.
25.人类的血型一般可分为A,B,AB,O型四种,宁波市中心血战2015年共有8万人无偿献血,血战统计人员由电脑随机选出20人,血型分别是: O,A,O,B,O,A,A,AB,A,O,O,B,AB,B,O,A,O,B,O,A. (1)请设计统计表分类统计这20人各类血型人数; (2)若每位献血者平均献血200毫升,一年中宁波市各医院O型血用血量约为6×106毫米,请你估计2015年这8万人所献的O型血是否够用?
26. (本题8分)某校为了解学生体质情况,从各年级学生中随机抽取部分学生进行体能测试. 每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制 成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题: / /
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
27.某中学开展“阳光体育一小时”活动.根据学校事假情况,决定开设四项运动项目:A:踢毽子;B:篮球;C:跳绳;D:乒乓球.为了解学生最喜欢哪一种运动项目,随机抽取了n名学生进行问卷调查,每位学生在问卷调查时都按要求只选择了其中一种喜欢的运动项目.收回全部问卷后,将收集到的数据整理并绘制成如下的统计图,若参与调查的学生中喜欢A方式的学生的人数占参与调查学生人数的40%.根据统计图提供的信息,解答下列问题: (1)求n的值. (2)求参与调查的学生中喜欢C的学生的人数. (3)根据统计结果,估计该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数. /
28.某班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况,八年级300名同学零花钱的最主要用途情况,九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据. /
时间
1小时左右
1.5小时左右
2小时左右
2.5小时左右
人数
50
80
120
50
根据以上信息,请回答下列问题: (1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少; (2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图; (3)九年级300名同学中完成家庭作业的平均时间大约是多少小时?(结果保留一位小数)
29.某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画.要求每位同学必须参加,且限报一项活动.以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图.请你结合图示所给出的信息解答下列问题.
?/
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
30.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某 食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A、B、C、D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图. 请根据以上信息回答: / ⑴本次参加抽样调查的居民有多少人? ⑵将不完整的条形图补充完整. ⑶若居民区有8000人,请估计爱吃D粽的人数? ⑷若有外型完全相同的A、B、C、D粽各一个煮熟后,小王吃了俩个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率?
答案解析部分
一、单选题
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】D
5.【答案】A
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】B
10.【答案】B
二、填空题
11.【答案】312
12.【答案】虽然甲、乙两名运动员的平均成绩相同,但乙运动员的成绩的方差较小,成绩稳定
13.【答案】24000
14.【答案】甲
15.【答案】①②③
16.【答案】400
17.【答案】1000
18.【答案】1800.
19.【答案】45
20.【答案】350
三、解答题
21.【答案】这组数据的平均数=(1.15+1.04+…+1.16)÷20=1.172(千克).能估计水库中鱼的平均重量,估计水库中鱼的平均重量为1.172千克
22.【答案】解:(1)八年级(5)班学生人数:2÷5%=40(人); (2)投中两次的人数:40-2-12-8=18(人), 18÷40×100%=45%,8÷40×100%=20%. 如图所示: / (3)360°×20%=72°; (4)200×(1-5%-30%)=130(人), 答:投中次数在2次以上(包括2次)的人数有130人.
23.【答案】(1)解:由条形统计图可得,女生进球数的平均数为:(1×1+2×4+1×3+4×2)÷8=2.5(个); ∵第4,5个数据都是2,则其平均数为:2; ∴女生进球数的中位数为:2 (2)解:样本中优秀率为:
3
8
, 故全校有女生1200人,“优秀”等级的女生为:1200×
3
8
=450(人), 答:“优秀”等级的女生约为450人
24.【答案】解:(1)90÷30%=300(名), 故一共调查了300名学生; (2)艺术的人数:300×20%=60(名), 其它的人数:300×10%=30(名); 补全折线图如图: / (3)体育部分所对应的圆心角的度数为:
40
300
×360°=48°; (4)1800×
80
300
=480(名).
25.【答案】解:(1)统计表格如图: / (2)
8
20
×8×
10
4
×200=6.4×
10
6
, 6.4×106>6×106 , 答:O型血够用.
26.【答案】(1)解:填写的统计表如图1所示: / (2)解:补全的条形统计图如图2所示: / (3)解:抽取的学生中体能测试的优秀率为:12÷50=24%; ∴该校体能测试为“优秀”的人数为1500×24%=360(人)
27.【答案】解:(1)80÷40%=200(人); (2)200﹣80﹣30﹣50=40(人); (3)
40?30
200
×1800=90(人), 答:该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多90人.
28.【答案】解:(1)冰红茶的百分比为100%﹣25%﹣25%﹣10%=40%,冰红茶的人数为400×40%=160(人), 即七年级同学最喜欢喝“冰红茶”的人数是160人; (2)补全频数分布直方图如右图所示. (3)
1×50+1.5×80+2×120+2.5×50
50+80+120+50
(小时). 答:九年级300名同学完成家庭作业的平均时间约为1.8小时. ?/
29.【答案】解:(1)学生的总数是:
20
40%
×100%=50(人),
参加书法比赛的学生所占的比例是:
10
50
×100%=20%,
则参加绘画比赛的学生所占的比例是:1﹣28%﹣40%﹣20%=12%,
(2)参加书法比赛的学生所占的比例是20%,
则扇形的圆心角的度数是:360×20%=72°;
(3)参加演讲比赛的人数是:600×28%=168(人),
参加唱歌比赛的人数是:600×40%=240(人).
30.【答案】解:(1)60÷10%=600(人). 答:本次参加抽样调查的居民有600人. (2)如图; / (3)8000×40%=3200(人). 答:该居民区有8000人,估计爱吃D粽的人有3200人。 (4)如图; / P(C粽)=
3
12
=
1
4
. 答:他第二个吃到的恰好是C粽的概率是
1
4
.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
