湘教版九年级上册《第三章图形的相似》单元检测试卷(含答案)
文档属性
| 名称 | 湘教版九年级上册《第三章图形的相似》单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-21 21:04:01 | ||
图片预览


文档简介
【专题突破训练】湘教版九年级数学上册 第三章 图形的相似 单元检测试卷
一、单选题(共10题;共30分)
1.若△ABC∽△A′B′C′且 /= /? , △ABC的周长为15cm,则△A′B′C′的周长为( )cm.
A.?18???????????????????????????????????????/B.?20???????????????????????????????????????/C.?/???????????????????????????????????????/D.?/?
2.如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=2,DB=4,则
????
????
的值为(?? ) /
A.?
1
2
??????????????????????????????????????????/B.?
1
3
??????????????????????????????????????????/C.?
1
4
??????????????????????????????????????????/D.?
1
6
3.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( ). /
A.?900cm?????????????????????????????/B.?1000cm?????????????????????????????/C.?1100cm?????????????????????????????/D.?1200cm
4.下列说法中:①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′位似,则在五边形中连线组成的△ABC与△A′B′C′也是位似的.正确的个数是( )
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
5.两个相似三角形的对应边分别为15㎝和23㎝,它们的周长差为40㎝,则这两个三角形的周长分别为?? (??? )
A.?75㎝,115㎝???????????????????????/B.?60㎝,100???????????????????????/C.?85㎝,125㎝???????????????????????/D.?45㎝,85㎝
6.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为(?? ) /
A.?10米???????????????????????????????????/B.?12米???????????????????????????????????/C.?15米???????????????????????????????????/D.?22.5米
7.如图,在Rt△ABC中,∠C=90°,CD⊥AB于D.已知AB=13,CD=6,则Rt△ABC的周长为( )
/
A.?13+5
13
?/B.?13+13
13
C.?13+9
15
?/D.?18
8.下列关于相似的说法:①所有的等腰直角三角形一定相似;②所有的菱形一定相似;③所有的全等三角形一定相似;④所有的有一个角为60°的等腰梯形一定相似.其中说法正确的有(??? )
A.?1个???????????????????????????????????????B.?4个???????????????????????????????????????C.?3个???????????????????????????????????????D.?2个
9.如图,点P在△ABC的边AC上,添加以下一个条件,不能判断△ABP∽△ACB的是(??? ) /
A.?∠ABP=∠C??????????????????????/B.?∠APB=∠ABC??????????????????????/C.?
????
????
=
????
????
??????????????????????/D.?
????
????
=
????
????
10.搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( ) /
A.?96cm2?????????????????????????????/B.?48cm2? ?????????????????????????????/C.?24cm2?????????????????????????????/D.?以上都不对
二、填空题(共10题;共30分)
11.如图,AD//BE//CF,直线
??
1
、
??
2
与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是________. /
12.已知△ABC∽△DEF, △?????? 与 △?????? 的相似比为4:1,则 △?????? 与 △?????? 对应边上的高之比为________.
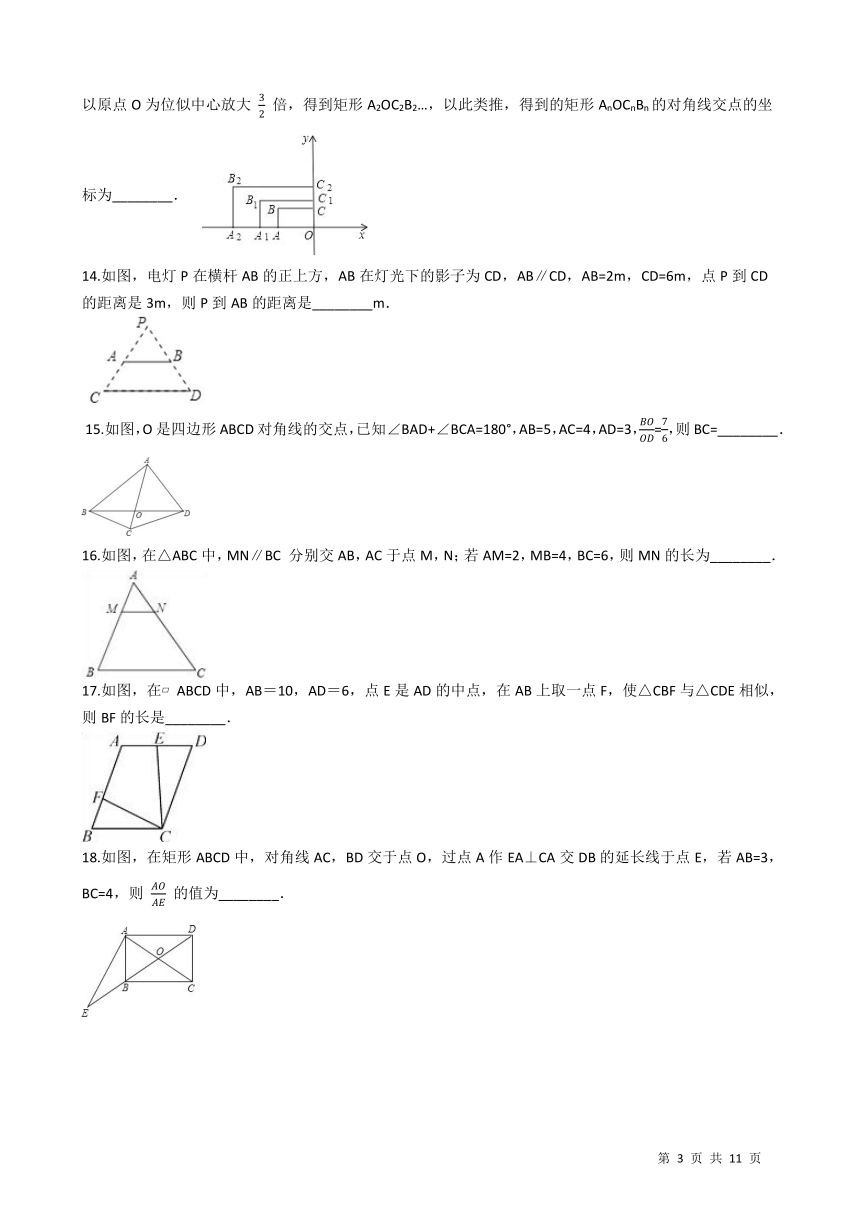
13.如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的
3
2
倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大
3
2
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为________. /
14.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是3m,则P到AB的距离是________m. / ?15.如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,
????
????
=
7
6
,则BC=________. /
16.如图,在△ABC中,MN∥BC 分别交AB,AC于点M,N;若AM=2,MB=4,BC=6,则MN的长为________.
17.如图,在?ABCD中,AB=10,AD=6,点E是AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是________.
/
18.如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则
????
????
的值为________. /
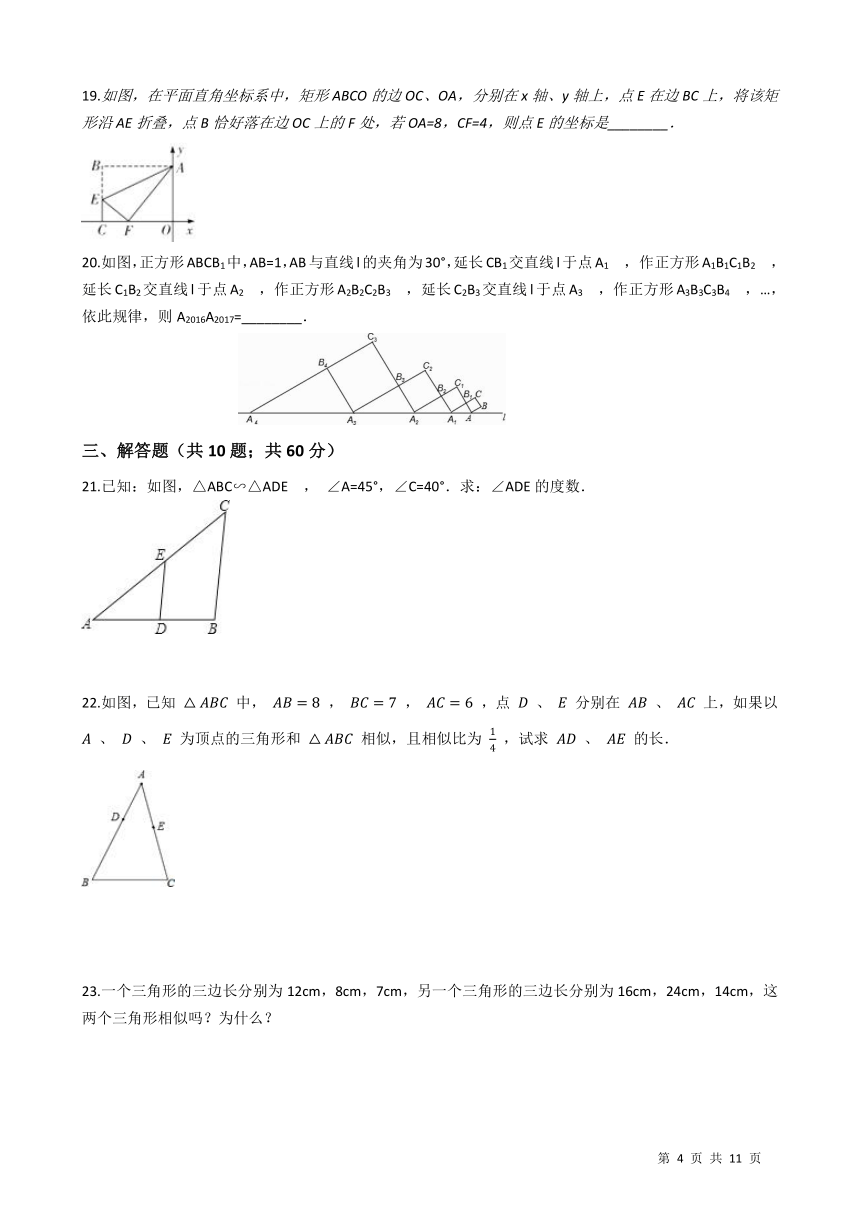
19.如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是________. /
20.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017=________.
三、解答题(共10题;共60分)
21.已知:如图,△ABC∽△ADE , ∠A=45°,∠C=40°.求:∠ADE的度数. /?
22.如图,已知 △?????? 中, ????=8 , ????=7 , ????=6 ,点 ?? 、 ?? 分别在 ???? 、 ???? 上,如果以 ?? 、 ?? 、 ?? 为顶点的三角形和 △?????? 相似,且相似比为
1
4
,试求 ???? 、 ???? 的长. /
23.一个三角形的三边长分别为12cm,8cm,7cm,另一个三角形的三边长分别为16cm,24cm,14cm,这两个三角形相似吗?为什么?
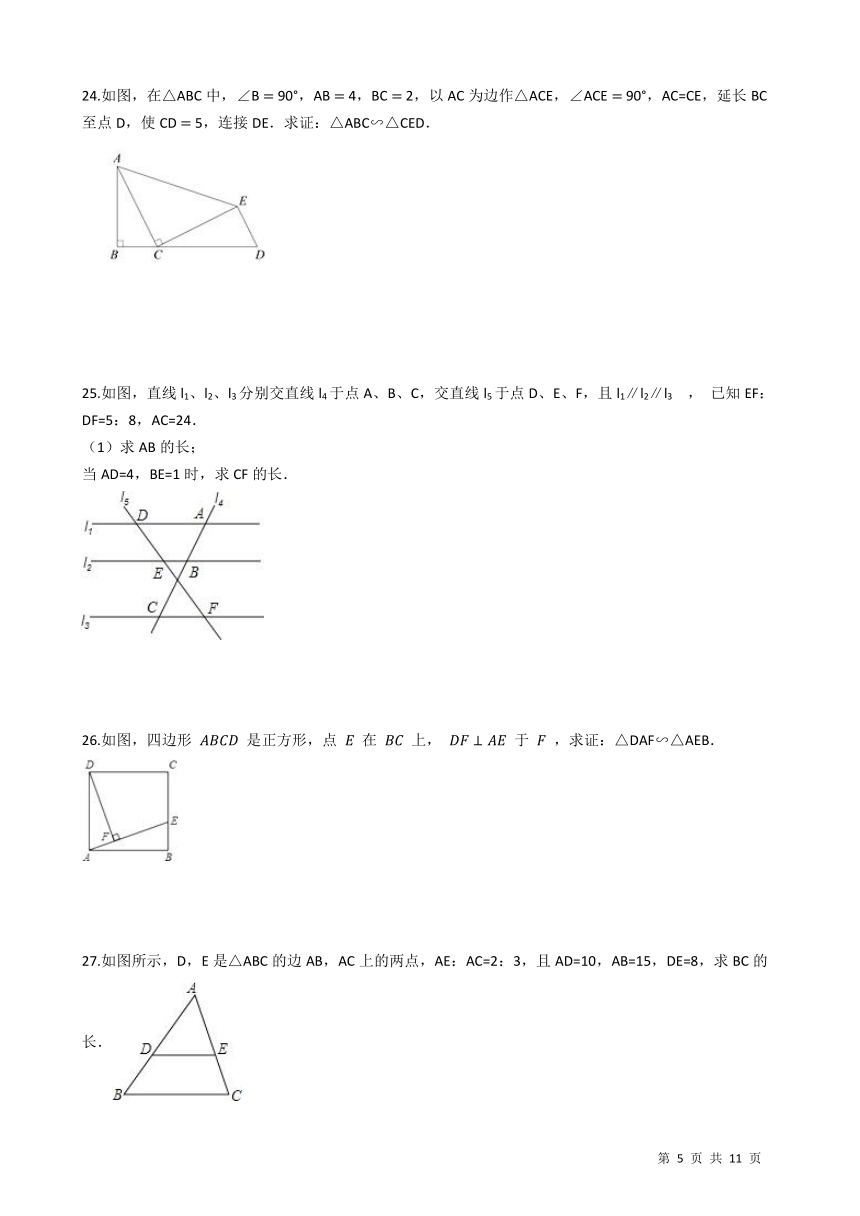
24.如图,在△ABC中,∠B = 90°,AB = 4,BC = 2,以AC为边作△ACE,∠ACE = 90°,AC=CE,延长BC至点D,使CD = 5,连接DE.求证:△ABC∽△CED. /
25.如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3 , 已知EF:DF=5:8,AC=24. (1)求AB的长; 当AD=4,BE=1时,求CF的长. /
26.如图,四边形 ???????? 是正方形,点 ?? 在 ???? 上, ????⊥???? 于 ?? ,求证:△DAF∽△AEB.
/
27.如图所示,D,E是△ABC的边AB,AC上的两点,AE:AC=2:3,且AD=10,AB=15,DE=8,求BC的长./
28.如图,某人在点A处测量树高,点A到树的距离AD为21米,将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面,此时,观察视线恰好经过标杆顶点E及树的顶点C,求此树CD的高. /
29.一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长. /
30.已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'. (1)如图1,∠AEE'= ??????°; /// (2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系; (3)如图3,在(2)的条件下,如果CE=2,AE=2
7
,求ME的长.
答案解析部分
一、单选题
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】A
7.【答案】A
8.【答案】D
9.【答案】D
10.【答案】B
二、填空题
11.【答案】3
12.【答案】4:1
13.【答案】(﹣
3
n
2
n
,
3
n
2
n+1
)
14.【答案】1
15.【答案】
14
5
16.【答案】2
17.【答案】1.8
18.【答案】
7
24
19.【答案】(-10,3)
20.【答案】2×31008
三、解答题
21.【答案】解答:∵△ABC∽△ADE , ∠C=40°, ∴∠AED=∠C=40°. 在△ADE中, ∵∠AED+∠ADE+∠A=180°,∠A=45° 即40°+∠ADE+45°=180°, ∴∠ADE=95°.
22.【答案】解:当 △??????∽△?????? 时,相似比为
1
4
,
????
????
=
????
????
=
1
4
, 即:
????
8
=
????
6
=
1
4
, 解得: ????=2 , ????=1.5 ; 当 △??????∽△?????? 时,
????
????
=
????
????
=
1
4
, 即:
????
6
=
????
8
=
1
4
,
解得: ????=1.5 , ????=2
23.【答案】解:∵
7????
14????
=
1
2
,
8????
16????
=
1
2
,
12????
24????
=
1
2
, ∴这两个三角形相似
24.【答案】解:∵ ∠B=90°,AB=4,BC=2, ∴ ????=
??
??
2
+??
??
2
=2
5
. ∵ CE=AC, ∴ ????=2
5
. ∵ CD=5, ∴
????
????
=
????
????
.????? ∵ ∠B=90°,∠ACE=90°, ∴ ∠BAC+∠BCA=90°,∠BCA+∠DCE=90°. ∴ ∠BAC=∠DCE. ∴ △ABC∽△CED.
25.【答案】解:(1)∵l1∥l2∥l3 , EF:DF=5:8,AC=24, ∴
????
????
=
????
????
=
5
8
, ∴
????
24
=
5
8
, ∴BC=15, ∴AB=AC﹣BC=24﹣15=9. (2)解:∵l1∥l2∥l3 , / ∴
????
????
=
????
????
=
1
4
, ∴
????
????+9
=
1
4
, ∴OB=3, ∴OC=BC﹣OB=15﹣3=12, ∴
????
????
=
????
????
=
3
12
, ∴
1
????
=
1
4
, ∴CF=4.
26.【答案】解: ∵四边形 ???????? 是正方形,
∴ ∠??????+∠??????=90° ,
∵ ????⊥???? 于 ?? ,
∴ ∠??????+∠??????=90° ,
∴ ∠??????=∠?????? ,
又∵ ∠??????=∠??=90° ,
∴△DAF∽△AEB.
27.【答案】解:∵AD=10,AB=15,∴AD:AB=10:15=2:3, 而AE:AC=2:3, ∴AE:AC=AD:AB, ∴DE∥BC, ∴△ADE∽△ABC, ∴
????
????
=
????
????
,即
8
????
=
2
3
, ∴BC=12.
28.【答案】解:∵ CD⊥AD,EB⊥AD, ∴ EB∥CD. ∴ △ABE∽△ADC. ∴
????
????
=
????
????
. ∵ EB=2,AB=3,AD=21, ∴
2
????
=
3
21
. ∴ CD=14. 答:此树高为14米.
29.【答案】解:∵四边形PQMN是矩形, ∴BC∥PQ, ∴△APQ∽△ABC, ∴
????
????
=
????
????
, 由于矩形长与宽的比为3:2, ∴分两种情况: ①若PQ为长,PN为宽, 设PQ=3k,PN=2k, 则
3??
12
=
8?2??
8
, 解得:k=2, ∴PQ=6cm,PN=4cm; ②PN为6,PQ为宽, 设PN=3k,PQ=2k, 则
2??
12
=
8?3??
8
, 解得:k=
24
13
, ∴PN=
72
13
cm,PQ=
48
13
cm; 综上所述:矩形的长为6cm,宽为4cm;或长为
72
13
cm,宽为
48
13
cm.
30.【答案】解:(1)根据题意知:AE=AE' ,∠E'AE=120°,所以∠AEE'=30°; (2)当点E在线段CD上时,设AF与EE'相交于N, ∵∠E'AE=120°,∠EAF=30°, ∴∠E'AN=90°,∠AE'N=30°, ∴AN=
1
2
E'N, ∵∠NAE=∠NEA=30°, ∴AN=EN,即EN=
1
2
NE', ∵ME∥BC ∴△MNE∽△FNE' ∴
????
??
′
??
=
????
??
′
??
=
1
2
,而E'B=DE, ∴DE+BF=2ME; 同理:当点E在CD的延长线上, 0°<∠EAD<30°时,BF-DE=2ME; 30°<∠EAD≤90°时,DE+BF=2ME;? 90°<∠EAD<120°时,DE-BF=2ME; (3)作AG⊥BC于点G, 作DH⊥BC于点H. / 由AD∥BC,AD=AB=CD,∠BAD=120°,得∠ABC=∠DCB=60°, 易知四边形AGHD是矩形和两个全等的直角三角形△ABG,△DCH. 则GH="AD" , BG=CH. ∵∠ABE'=∠ADC=120°, ∴点E'、B、C在一条直线上. 设AD=AB=CD=x,则GH=x,BG=CH=
1
2
??,. 作EQ⊥BC于Q. 在Rt△EQC中,CE=2,∠C=60°, ∴CQ=1,EQ=
3
. ∴E'Q=BC-CQ+BE'=2x-1+x-2=3x-3. 作AP⊥EE'于点P. ∵△ADE绕点A顺时针旋转120°后,得到△ABE'. ∴△AEE'是等腰三角形,∠AEE'=30°,AE'=AE=2
7
. ∴在Rt△APE'中,E'P=
21
. ∴EE'=2E'P=2
21
.?? ∴在Rt△EQ E'中,E'Q=
??
′
??
2
???
??
2
=9. ∴3x-3=9. ∴x=4. ∴DE=BE'=2,BC=8,BG=2. ∴E'G=4 在Rt△E'AF中,AG⊥BC, ∴Rt△AG E'∽Rt△FA E'. ∴
????′
??′??
=
??′??
????′
∴E'F=7. ∴BF=E'F-E'B=5. 由(2)知:DE+BF=2ME ∴ME=
7
2
.
一、单选题(共10题;共30分)
1.若△ABC∽△A′B′C′且 /= /? , △ABC的周长为15cm,则△A′B′C′的周长为( )cm.
A.?18???????????????????????????????????????/B.?20???????????????????????????????????????/C.?/???????????????????????????????????????/D.?/?
2.如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=2,DB=4,则
????
????
的值为(?? ) /
A.?
1
2
??????????????????????????????????????????/B.?
1
3
??????????????????????????????????????????/C.?
1
4
??????????????????????????????????????????/D.?
1
6
3.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:如图1,甲组测得一根直立于平地,长为80cm的竹竿的影长为60cm.如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为( ). /
A.?900cm?????????????????????????????/B.?1000cm?????????????????????????????/C.?1100cm?????????????????????????????/D.?1200cm
4.下列说法中:①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A′B′C′D′E′位似,则在五边形中连线组成的△ABC与△A′B′C′也是位似的.正确的个数是( )
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
5.两个相似三角形的对应边分别为15㎝和23㎝,它们的周长差为40㎝,则这两个三角形的周长分别为?? (??? )
A.?75㎝,115㎝???????????????????????/B.?60㎝,100???????????????????????/C.?85㎝,125㎝???????????????????????/D.?45㎝,85㎝
6.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为(?? ) /
A.?10米???????????????????????????????????/B.?12米???????????????????????????????????/C.?15米???????????????????????????????????/D.?22.5米
7.如图,在Rt△ABC中,∠C=90°,CD⊥AB于D.已知AB=13,CD=6,则Rt△ABC的周长为( )
/
A.?13+5
13
?/B.?13+13
13
C.?13+9
15
?/D.?18
8.下列关于相似的说法:①所有的等腰直角三角形一定相似;②所有的菱形一定相似;③所有的全等三角形一定相似;④所有的有一个角为60°的等腰梯形一定相似.其中说法正确的有(??? )
A.?1个???????????????????????????????????????B.?4个???????????????????????????????????????C.?3个???????????????????????????????????????D.?2个
9.如图,点P在△ABC的边AC上,添加以下一个条件,不能判断△ABP∽△ACB的是(??? ) /
A.?∠ABP=∠C??????????????????????/B.?∠APB=∠ABC??????????????????????/C.?
????
????
=
????
????
??????????????????????/D.?
????
????
=
????
????
10.搬进新居后,小杰自己动手用彩塑纸做了一个如图所示的正方形的挂式小饰品ABCD,彩线BD.AN.CM将正方形ABCD分成六部分,其中M是AB的中点,N是BC的中点,AN与CM交于O点.已知正方形ABCD的面积为576cm2 , 则被分隔开的△CON的面积为( ) /
A.?96cm2?????????????????????????????/B.?48cm2? ?????????????????????????????/C.?24cm2?????????????????????????????/D.?以上都不对
二、填空题(共10题;共30分)
11.如图,AD//BE//CF,直线
??
1
、
??
2
与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是________. /
12.已知△ABC∽△DEF, △?????? 与 △?????? 的相似比为4:1,则 △?????? 与 △?????? 对应边上的高之比为________.
13.如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的
3
2
倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大
3
2
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为________. /
14.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是3m,则P到AB的距离是________m. / ?15.如图,O是四边形ABCD对角线的交点,已知∠BAD+∠BCA=180°,AB=5,AC=4,AD=3,
????
????
=
7
6
,则BC=________. /
16.如图,在△ABC中,MN∥BC 分别交AB,AC于点M,N;若AM=2,MB=4,BC=6,则MN的长为________.
17.如图,在?ABCD中,AB=10,AD=6,点E是AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是________.
/
18.如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则
????
????
的值为________. /
19.如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是________. /
20.如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017=________.
三、解答题(共10题;共60分)
21.已知:如图,△ABC∽△ADE , ∠A=45°,∠C=40°.求:∠ADE的度数. /?
22.如图,已知 △?????? 中, ????=8 , ????=7 , ????=6 ,点 ?? 、 ?? 分别在 ???? 、 ???? 上,如果以 ?? 、 ?? 、 ?? 为顶点的三角形和 △?????? 相似,且相似比为
1
4
,试求 ???? 、 ???? 的长. /
23.一个三角形的三边长分别为12cm,8cm,7cm,另一个三角形的三边长分别为16cm,24cm,14cm,这两个三角形相似吗?为什么?
24.如图,在△ABC中,∠B = 90°,AB = 4,BC = 2,以AC为边作△ACE,∠ACE = 90°,AC=CE,延长BC至点D,使CD = 5,连接DE.求证:△ABC∽△CED. /
25.如图,直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3 , 已知EF:DF=5:8,AC=24. (1)求AB的长; 当AD=4,BE=1时,求CF的长. /
26.如图,四边形 ???????? 是正方形,点 ?? 在 ???? 上, ????⊥???? 于 ?? ,求证:△DAF∽△AEB.
/
27.如图所示,D,E是△ABC的边AB,AC上的两点,AE:AC=2:3,且AD=10,AB=15,DE=8,求BC的长./
28.如图,某人在点A处测量树高,点A到树的距离AD为21米,将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面,此时,观察视线恰好经过标杆顶点E及树的顶点C,求此树CD的高. /
29.一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长. /
30.已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'. (1)如图1,∠AEE'= ??????°; /// (2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系; (3)如图3,在(2)的条件下,如果CE=2,AE=2
7
,求ME的长.
答案解析部分
一、单选题
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】A
7.【答案】A
8.【答案】D
9.【答案】D
10.【答案】B
二、填空题
11.【答案】3
12.【答案】4:1
13.【答案】(﹣
3
n
2
n
,
3
n
2
n+1
)
14.【答案】1
15.【答案】
14
5
16.【答案】2
17.【答案】1.8
18.【答案】
7
24
19.【答案】(-10,3)
20.【答案】2×31008
三、解答题
21.【答案】解答:∵△ABC∽△ADE , ∠C=40°, ∴∠AED=∠C=40°. 在△ADE中, ∵∠AED+∠ADE+∠A=180°,∠A=45° 即40°+∠ADE+45°=180°, ∴∠ADE=95°.
22.【答案】解:当 △??????∽△?????? 时,相似比为
1
4
,
????
????
=
????
????
=
1
4
, 即:
????
8
=
????
6
=
1
4
, 解得: ????=2 , ????=1.5 ; 当 △??????∽△?????? 时,
????
????
=
????
????
=
1
4
, 即:
????
6
=
????
8
=
1
4
,
解得: ????=1.5 , ????=2
23.【答案】解:∵
7????
14????
=
1
2
,
8????
16????
=
1
2
,
12????
24????
=
1
2
, ∴这两个三角形相似
24.【答案】解:∵ ∠B=90°,AB=4,BC=2, ∴ ????=
??
??
2
+??
??
2
=2
5
. ∵ CE=AC, ∴ ????=2
5
. ∵ CD=5, ∴
????
????
=
????
????
.????? ∵ ∠B=90°,∠ACE=90°, ∴ ∠BAC+∠BCA=90°,∠BCA+∠DCE=90°. ∴ ∠BAC=∠DCE. ∴ △ABC∽△CED.
25.【答案】解:(1)∵l1∥l2∥l3 , EF:DF=5:8,AC=24, ∴
????
????
=
????
????
=
5
8
, ∴
????
24
=
5
8
, ∴BC=15, ∴AB=AC﹣BC=24﹣15=9. (2)解:∵l1∥l2∥l3 , / ∴
????
????
=
????
????
=
1
4
, ∴
????
????+9
=
1
4
, ∴OB=3, ∴OC=BC﹣OB=15﹣3=12, ∴
????
????
=
????
????
=
3
12
, ∴
1
????
=
1
4
, ∴CF=4.
26.【答案】解: ∵四边形 ???????? 是正方形,
∴ ∠??????+∠??????=90° ,
∵ ????⊥???? 于 ?? ,
∴ ∠??????+∠??????=90° ,
∴ ∠??????=∠?????? ,
又∵ ∠??????=∠??=90° ,
∴△DAF∽△AEB.
27.【答案】解:∵AD=10,AB=15,∴AD:AB=10:15=2:3, 而AE:AC=2:3, ∴AE:AC=AD:AB, ∴DE∥BC, ∴△ADE∽△ABC, ∴
????
????
=
????
????
,即
8
????
=
2
3
, ∴BC=12.
28.【答案】解:∵ CD⊥AD,EB⊥AD, ∴ EB∥CD. ∴ △ABE∽△ADC. ∴
????
????
=
????
????
. ∵ EB=2,AB=3,AD=21, ∴
2
????
=
3
21
. ∴ CD=14. 答:此树高为14米.
29.【答案】解:∵四边形PQMN是矩形, ∴BC∥PQ, ∴△APQ∽△ABC, ∴
????
????
=
????
????
, 由于矩形长与宽的比为3:2, ∴分两种情况: ①若PQ为长,PN为宽, 设PQ=3k,PN=2k, 则
3??
12
=
8?2??
8
, 解得:k=2, ∴PQ=6cm,PN=4cm; ②PN为6,PQ为宽, 设PN=3k,PQ=2k, 则
2??
12
=
8?3??
8
, 解得:k=
24
13
, ∴PN=
72
13
cm,PQ=
48
13
cm; 综上所述:矩形的长为6cm,宽为4cm;或长为
72
13
cm,宽为
48
13
cm.
30.【答案】解:(1)根据题意知:AE=AE' ,∠E'AE=120°,所以∠AEE'=30°; (2)当点E在线段CD上时,设AF与EE'相交于N, ∵∠E'AE=120°,∠EAF=30°, ∴∠E'AN=90°,∠AE'N=30°, ∴AN=
1
2
E'N, ∵∠NAE=∠NEA=30°, ∴AN=EN,即EN=
1
2
NE', ∵ME∥BC ∴△MNE∽△FNE' ∴
????
??
′
??
=
????
??
′
??
=
1
2
,而E'B=DE, ∴DE+BF=2ME; 同理:当点E在CD的延长线上, 0°<∠EAD<30°时,BF-DE=2ME; 30°<∠EAD≤90°时,DE+BF=2ME;? 90°<∠EAD<120°时,DE-BF=2ME; (3)作AG⊥BC于点G, 作DH⊥BC于点H. / 由AD∥BC,AD=AB=CD,∠BAD=120°,得∠ABC=∠DCB=60°, 易知四边形AGHD是矩形和两个全等的直角三角形△ABG,△DCH. 则GH="AD" , BG=CH. ∵∠ABE'=∠ADC=120°, ∴点E'、B、C在一条直线上. 设AD=AB=CD=x,则GH=x,BG=CH=
1
2
??,. 作EQ⊥BC于Q. 在Rt△EQC中,CE=2,∠C=60°, ∴CQ=1,EQ=
3
. ∴E'Q=BC-CQ+BE'=2x-1+x-2=3x-3. 作AP⊥EE'于点P. ∵△ADE绕点A顺时针旋转120°后,得到△ABE'. ∴△AEE'是等腰三角形,∠AEE'=30°,AE'=AE=2
7
. ∴在Rt△APE'中,E'P=
21
. ∴EE'=2E'P=2
21
.?? ∴在Rt△EQ E'中,E'Q=
??
′
??
2
???
??
2
=9. ∴3x-3=9. ∴x=4. ∴DE=BE'=2,BC=8,BG=2. ∴E'G=4 在Rt△E'AF中,AG⊥BC, ∴Rt△AG E'∽Rt△FA E'. ∴
????′
??′??
=
??′??
????′
∴E'F=7. ∴BF=E'F-E'B=5. 由(2)知:DE+BF=2ME ∴ME=
7
2
.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
