【专题突破】九年级数学下第27章圆单元检测试卷(附答案)
文档属性
| 名称 | 【专题突破】九年级数学下第27章圆单元检测试卷(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-23 22:49:00 | ||
图片预览



文档简介
【专题突破训练】华师大版九年级数学下册 第27章 圆 单元检测试卷
一、单选题(共11题;共33分)
1.已知扇形的圆心角为120°,半径为6cm,则扇形的面积为(????)
A.?12??
??
2
???????????????????????????????B.?36??
??
2
???????????????????????????????C.?12π??
??
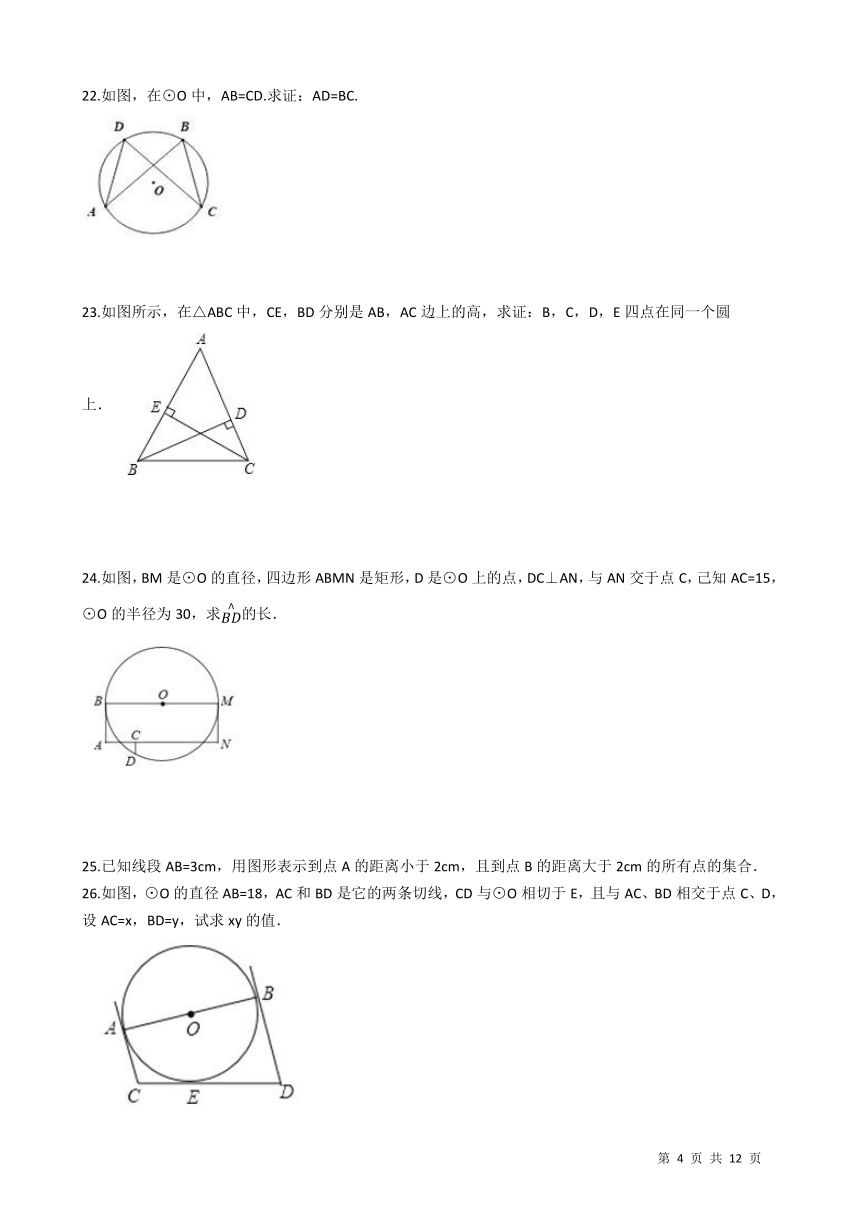
2
???????????????????????????????D.?36π??
??
2
2.如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为(?? ) /
A.?84°???????????????????????????????????????B.?60°???????????????????????????????????????C.?36°???????????????????????????????????????D.?24°
3.如图,已知A,B,C为⊙O上三点,若∠AOB=80°,则∠ACB度数为(???? )
/
A.?80°???????????????????????????????????????B.?70°???????????????????????????????????????C.?60°???????????????????????????????????????D.?40°
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,求直角三角形能容纳的圆形(内切圆)直径” 则该圆的直径为(?? ) /
A.?3步???????????????????????????????????????B.?5步???????????????????????????????????????C.?6步???????????????????????????????????????D.?8步
5.已知矩形ABCD的一边AB=4cm,另一边BC=2cm,以直线AB为轴旋转一周,所得到的圆柱的表面积是( )
A.?12πcm2????????????????????????????/B.?16πcm2????????????????????????????/C.?20πcm2????????????????????????????/D.?24πcm2
6.一个圆锥的母线长是10,高为8,那么这个圆锥的表面积是? (??????? )
A.?116π?????????????????????????????????????B.?96π?????????????????????????????????????C.?80π?????????????????????????????????????D.?60π
7.一个几何体的三视图如图所示,根据图中的相关数据求得该几何体的侧面积为( ) /
A.?π?????????????????????????????????????????B.?2π?????????????????????????????????????????C.?3π?????????????????????????????????????????D.?4π
8.如图,△ABC内接于⊙O,∠ABC=71°,∠CAB=53°,点D在AC弧上,则∠ADB的大小为 /
A.?46°???????????????????????????????????????B.?53°???????????????????????????????????????C.?56°???????????????????????????????????????D.?71°
9.若一个圆锥的底面半径为3cm,母线长为5cm,则这个圆锥的全面积为(????)
A.?15π cm2???????????????????????????/B.?24π cm2???????????????????????????/C.?39π cm2???????????????????????????/D.?48π cm2
10.如图,一段公路的转弯处是一段圆弧
????
,则
????
的展直长度为(?? )
/
A.3π B.6π C.9π D.12π
11.如图点A,D,G,B在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a, EF=b, NH=c,则下列说法正确的是(??? ) /
A.?a>b>c????????????????????????????B.?a=b=c ?????????????????????????????C.?c>a>b????????????????????????????D.?b>c>a?
二、填空题(共9题;共27分)
12.圆锥体的底面周长为6π,侧面积为15π,则该圆锥体的高为________.
13.如图,△ABC内接于⊙O,AD是⊙O直径,若∠ABC=50°,则∠CAD=________度. /
14.如图,AB是⊙O的直径,点C、D在圆上,∠D=68°,则∠ABC等于?________. /?
15.如图,在△ABC中,BC=4,以点A为圆心、2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是________(结果保留π). /
16.如图,⊙O的内接四边形ABCD中,∠A=110°,则∠BOD等于________°. /
17.如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为________./
18.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
/
19.如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②
????
????
=
3
2
;③S△PDQ=
1
8
;④cos∠ADQ=
3
5
,其中正确结论是________(填写序号) /
20.如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2
3
,则图中阴影部分面积是________(结果保留π和根号) /
三、解答题(共10题;共60分)
21.如图⊙O是△ABC的外接圆,圆心O在这个三角形的高AD上,AB=10,BC=12,求⊙O的半径. /
22.如图,在⊙O中,AB=CD.求证:AD=BC. /
23.如图所示,在△ABC中,CE,BD分别是AB,AC边上的高,求证:B,C,D,E四点在同一个圆上. /
24.如图,BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上的点,DC⊥AN,与AN交于点C,己知AC=15,⊙O的半径为30,求
????
∧
的长. /
25.已知线段AB=3cm,用图形表示到点A的距离小于2cm,且到点B的距离大于2cm的所有点的集合.
26.如图,⊙O的直径AB=18,AC和BD是它的两条切线,CD与⊙O相切于E,且与AC、BD相交于点C、D,设AC=x,BD=y,试求xy的值. /
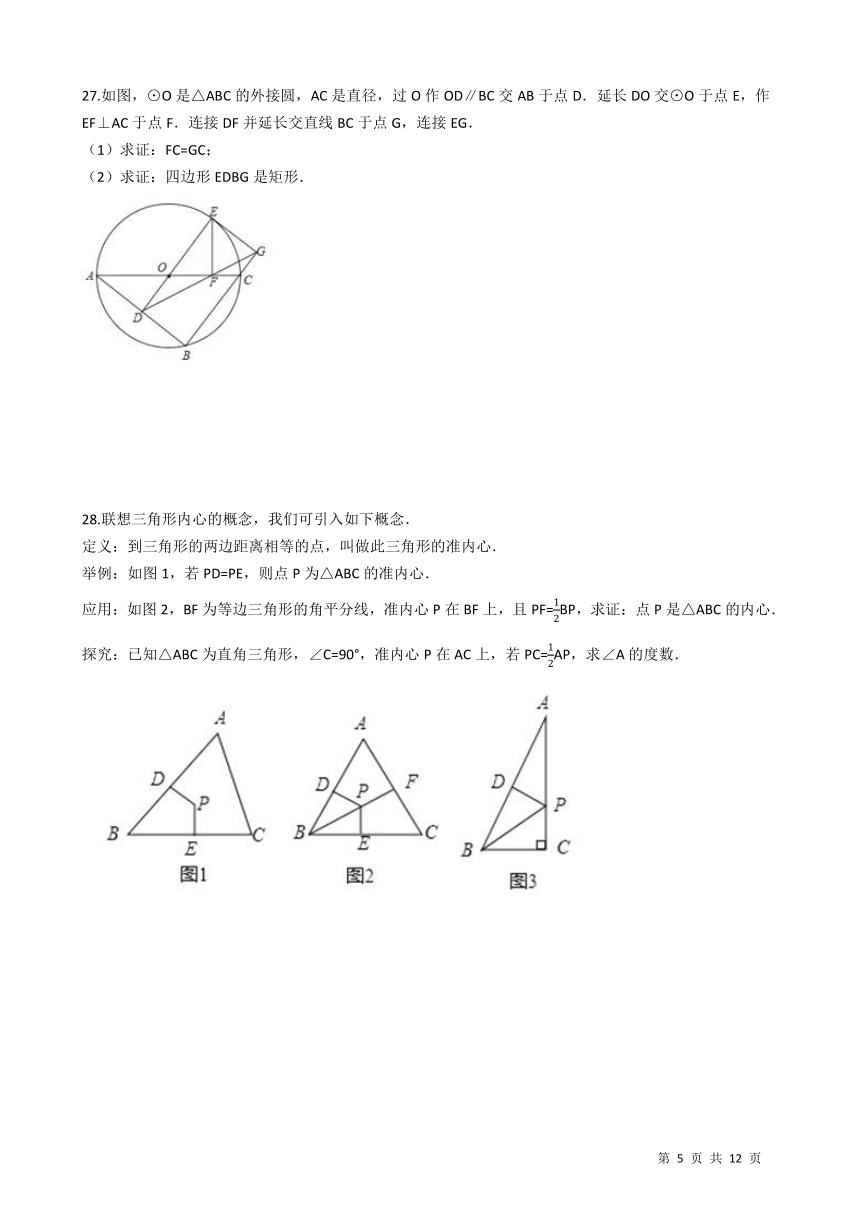
27.如图,⊙O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D.延长DO交⊙O于点E,作EF⊥AC于点F.连接DF并延长交直线BC于点G,连接EG. (1)求证:FC=GC; (2)求证:四边形EDBG是矩形. /
28.联想三角形内心的概念,我们可引入如下概念. 定义:到三角形的两边距离相等的点,叫做此三角形的准内心. 举例:如图1,若PD=PE,则点P为△ABC的准内心. 应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=
1
2
BP,求证:点P是△ABC的内心. 探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=
1
2
AP,求∠A的度数. /
29.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D.求AD的长. /
30.(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是????? . / (2)如图2,⊙O的半径为2,∠AOB=120°, ①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由. ②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由. /
(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是________.
(2)如图2,⊙O的半径为2,∠AOB=120°, ①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由. ②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.
答案解析部分
一、单选题
1.【答案】C
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】B
10.【答案】B
11.【答案】B
二、填空题
12.【答案】4
13.【答案】40
14.【答案】22°
15.【答案】4﹣
8??
9
16.【答案】140
17.【答案】9
18.【答案】52
19.【答案】①②④
20.【答案】3π﹣2
3
三、解答题
21.【答案】解:如图,连接OB. / ∵AD是△ABC的高. ∴BD=
1
2
BC=6 在Rt△ABD中,AD=
??
??
2
???
??
2
=
100?36
=8. 设圆的半径是R. 则OD=8﹣R. 在Rt△OBD中,根据勾股定理可以得到:R2=36+(8﹣R)2 解得:R=
25
4
.
22.【答案】证明:∵AB=CD,∴
????
=
????
, ∴
????
?
????
=
????
?
????
,即
????
=
????
? ∴ AD=BC?
23.【答案】证明:如图所示,取BC的中点F,连接DF,EF. ∵BD,CE是△ABC的高, ∴△BCD和△BCE都是直角三角形. ∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线, ∴DF=EF=BF=CF. ∴E,B,C,D四点在以F点为圆心, /BC为半径的圆上. /
24.【答案】解:连接OD,BD,延长DC交BM于点E, ∵BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上一点,DC⊥AN, ∴DE⊥BO, ∵AC=15cm, ∴BE=EO=15cm, ∵DO=30cm, ∴cos∠EOD=
????
????
=
1
2
, ∴∠EOD=60°, ∴
????
∧
=
60×π×30
180
=10π(cm). /
25.【答案】解:如图: 阴影部分就是到点A的距离小于2cm,且到点B的距离大于2cm的所有点组成的图形 /?
26.【答案】解:连接OC,OD. ∵AB=18,∴OA=OB=9, ∵AC和BD是它的两条切线, ∴OA⊥AC,OB⊥BD, ∴AC∥BD, ∴∠ACD+∠BDE=180°, ∴∠OCD+∠ODC=90°, ∵AC=x,BD=y, ∴OC=
??
2
+81
,OD=
??
2
+81
, ∵CD是圆O的切线, ∴CE=AC=x,DE=BD=y, ∴OC2+OD2=CD2 , 即x2+81+y2+81=(x+y)2 , 整理得2xy=162, ∴xy=81. /
27.【答案】证明(1)∵AC为直径,∴∠ABC=90°, ∵OD∥BC,∴∠ADO=∠ABC=90°, 在△AOD和△EOF中,
∠??????=∠??????
∠??????=∠??????
????=????
∴△AOD≌△EOF, ∴OD=OF, ∴∠ODF=∠OFD, ∵OD∥BC,∴∠FGC=∠ODF, 又∠GFC=∠OFD, ∴∠CFG=∠FGC, ∴FC=GC; (2)连接AE、EC, ∵OA=OE,∴∠OAE=∠OEA, ∵OD=OF,∴∠ODF=∠OFD, ∴∠OAE=∠OFD, ∴AE∥DG, ∵AC为直径,∴∠AEC=90°,又CF=CG, ∴CE是FG的垂直平分线, ∴△EFC≌△EGC, ∴∠EGC=∠EFC=90°, 又∠EDB=90°,∠ABC=90°, ∴四边形EDBG是矩形. /
28.【答案】解:应用:∵△ABC是等边三角形, ∴∠ABC=60°, ∵BF为角平分线, ∴∠PBE=30°, ∴PE=
1
2
PB, ∵BF是等边△ABC的角平分线, ∴BF⊥AC, ∵PF=
1
2
BF, ∴PE=PD=PF, ∴P是△ABC的内心; 探究:根据题意得: PD=PC=
1
2
AP, ∵sin??=
????
????
=
1
2
????
????
=
1
2
, ∴∠A是锐角, ∴∠A=30°.
29.【答案】解:过点C作CE⊥AD于点E, / 则AE=DE, ∵∠ACB=90°,AC=3,BC=4, ∴AB= /=5, ∵S△ABC= /AC?BC= /AB?CE, ∴CE= /= /= /, ∴AE= /= /, ∴AD=2AE= /.
30.【答案】(1)相切 (2)解:①存在 ∵PA=PB, ∴点P为∠AOB的平分线或反向延长线与⊙O的交点, 如图2, 当P点在优弧AB上时, 设⊙Q的半径为/, 若⊙Q与⊙O内切,可得2+(2-x)=2x,解得x=
4
3
, 若⊙Q与⊙O外切,可得2+(x+2)=2x,?解得x=4 , 当P点在劣弧AB上时, 同理可得:x=8
3
-12,x=8
3
+12 , 综上所述,存在⊙Q,半径可以为
4
3
,4 ,8
3
-12,8
3
+12; ②存在.作QH⊥PB于H,如图3, ∵PA⊥PB, ∴∠APB=90°, ∵⊙Q与射线PA.PB相切, ∴PQ平分∠APB, ∴∠QPH=45°, ∴△QHP为等腰直角三角形, ∴QH=PH, 在Rt△POA中,∠AOP=60°,OA=2, ∴OP=1, 设⊙Q的半径为r,即PH=QH=r,则OH=PH﹣OP=r﹣1, 在Rt△OQH中,OQ2=OH2+QH2=(r﹣1)2+r2, 若⊙Q与⊙O内切时,OQ=2﹣r,则(2﹣r)2=(r﹣1)2+r2,解得r1=1,r2=﹣3(舍去); 若⊙Q与⊙O外切时,OQ=2+r,则(2+r)2=(r﹣1)2+r2,解得r1=3+2
3
,r2=3-2
3
(舍去); 综上所述,存在⊙Q,其半径可以为1,3+2
3
. /.
一、单选题(共11题;共33分)
1.已知扇形的圆心角为120°,半径为6cm,则扇形的面积为(????)
A.?12??
??
2
???????????????????????????????B.?36??
??
2
???????????????????????????????C.?12π??
??
2
???????????????????????????????D.?36π??
??
2
2.如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为(?? ) /
A.?84°???????????????????????????????????????B.?60°???????????????????????????????????????C.?36°???????????????????????????????????????D.?24°
3.如图,已知A,B,C为⊙O上三点,若∠AOB=80°,则∠ACB度数为(???? )
/
A.?80°???????????????????????????????????????B.?70°???????????????????????????????????????C.?60°???????????????????????????????????????D.?40°
4.《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,求直角三角形能容纳的圆形(内切圆)直径” 则该圆的直径为(?? ) /
A.?3步???????????????????????????????????????B.?5步???????????????????????????????????????C.?6步???????????????????????????????????????D.?8步
5.已知矩形ABCD的一边AB=4cm,另一边BC=2cm,以直线AB为轴旋转一周,所得到的圆柱的表面积是( )
A.?12πcm2????????????????????????????/B.?16πcm2????????????????????????????/C.?20πcm2????????????????????????????/D.?24πcm2
6.一个圆锥的母线长是10,高为8,那么这个圆锥的表面积是? (??????? )
A.?116π?????????????????????????????????????B.?96π?????????????????????????????????????C.?80π?????????????????????????????????????D.?60π
7.一个几何体的三视图如图所示,根据图中的相关数据求得该几何体的侧面积为( ) /
A.?π?????????????????????????????????????????B.?2π?????????????????????????????????????????C.?3π?????????????????????????????????????????D.?4π
8.如图,△ABC内接于⊙O,∠ABC=71°,∠CAB=53°,点D在AC弧上,则∠ADB的大小为 /
A.?46°???????????????????????????????????????B.?53°???????????????????????????????????????C.?56°???????????????????????????????????????D.?71°
9.若一个圆锥的底面半径为3cm,母线长为5cm,则这个圆锥的全面积为(????)
A.?15π cm2???????????????????????????/B.?24π cm2???????????????????????????/C.?39π cm2???????????????????????????/D.?48π cm2
10.如图,一段公路的转弯处是一段圆弧
????
,则
????
的展直长度为(?? )
/
A.3π B.6π C.9π D.12π
11.如图点A,D,G,B在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a, EF=b, NH=c,则下列说法正确的是(??? ) /
A.?a>b>c????????????????????????????B.?a=b=c ?????????????????????????????C.?c>a>b????????????????????????????D.?b>c>a?
二、填空题(共9题;共27分)
12.圆锥体的底面周长为6π,侧面积为15π,则该圆锥体的高为________.
13.如图,△ABC内接于⊙O,AD是⊙O直径,若∠ABC=50°,则∠CAD=________度. /
14.如图,AB是⊙O的直径,点C、D在圆上,∠D=68°,则∠ABC等于?________. /?
15.如图,在△ABC中,BC=4,以点A为圆心、2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是________(结果保留π). /
16.如图,⊙O的内接四边形ABCD中,∠A=110°,则∠BOD等于________°. /
17.如图,顺次连接圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为________./
18.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
/
19.如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②
????
????
=
3
2
;③S△PDQ=
1
8
;④cos∠ADQ=
3
5
,其中正确结论是________(填写序号) /
20.如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2
3
,则图中阴影部分面积是________(结果保留π和根号) /
三、解答题(共10题;共60分)
21.如图⊙O是△ABC的外接圆,圆心O在这个三角形的高AD上,AB=10,BC=12,求⊙O的半径. /
22.如图,在⊙O中,AB=CD.求证:AD=BC. /
23.如图所示,在△ABC中,CE,BD分别是AB,AC边上的高,求证:B,C,D,E四点在同一个圆上. /
24.如图,BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上的点,DC⊥AN,与AN交于点C,己知AC=15,⊙O的半径为30,求
????
∧
的长. /
25.已知线段AB=3cm,用图形表示到点A的距离小于2cm,且到点B的距离大于2cm的所有点的集合.
26.如图,⊙O的直径AB=18,AC和BD是它的两条切线,CD与⊙O相切于E,且与AC、BD相交于点C、D,设AC=x,BD=y,试求xy的值. /
27.如图,⊙O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D.延长DO交⊙O于点E,作EF⊥AC于点F.连接DF并延长交直线BC于点G,连接EG. (1)求证:FC=GC; (2)求证:四边形EDBG是矩形. /
28.联想三角形内心的概念,我们可引入如下概念. 定义:到三角形的两边距离相等的点,叫做此三角形的准内心. 举例:如图1,若PD=PE,则点P为△ABC的准内心. 应用:如图2,BF为等边三角形的角平分线,准内心P在BF上,且PF=
1
2
BP,求证:点P是△ABC的内心. 探究:已知△ABC为直角三角形,∠C=90°,准内心P在AC上,若PC=
1
2
AP,求∠A的度数. /
29.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D.求AD的长. /
30.(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是????? . / (2)如图2,⊙O的半径为2,∠AOB=120°, ①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由. ②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由. /
(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是________.
(2)如图2,⊙O的半径为2,∠AOB=120°, ①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由. ②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.
答案解析部分
一、单选题
1.【答案】C
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】D
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】B
10.【答案】B
11.【答案】B
二、填空题
12.【答案】4
13.【答案】40
14.【答案】22°
15.【答案】4﹣
8??
9
16.【答案】140
17.【答案】9
18.【答案】52
19.【答案】①②④
20.【答案】3π﹣2
3
三、解答题
21.【答案】解:如图,连接OB. / ∵AD是△ABC的高. ∴BD=
1
2
BC=6 在Rt△ABD中,AD=
??
??
2
???
??
2
=
100?36
=8. 设圆的半径是R. 则OD=8﹣R. 在Rt△OBD中,根据勾股定理可以得到:R2=36+(8﹣R)2 解得:R=
25
4
.
22.【答案】证明:∵AB=CD,∴
????
=
????
, ∴
????
?
????
=
????
?
????
,即
????
=
????
? ∴ AD=BC?
23.【答案】证明:如图所示,取BC的中点F,连接DF,EF. ∵BD,CE是△ABC的高, ∴△BCD和△BCE都是直角三角形. ∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线, ∴DF=EF=BF=CF. ∴E,B,C,D四点在以F点为圆心, /BC为半径的圆上. /
24.【答案】解:连接OD,BD,延长DC交BM于点E, ∵BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上一点,DC⊥AN, ∴DE⊥BO, ∵AC=15cm, ∴BE=EO=15cm, ∵DO=30cm, ∴cos∠EOD=
????
????
=
1
2
, ∴∠EOD=60°, ∴
????
∧
=
60×π×30
180
=10π(cm). /
25.【答案】解:如图: 阴影部分就是到点A的距离小于2cm,且到点B的距离大于2cm的所有点组成的图形 /?
26.【答案】解:连接OC,OD. ∵AB=18,∴OA=OB=9, ∵AC和BD是它的两条切线, ∴OA⊥AC,OB⊥BD, ∴AC∥BD, ∴∠ACD+∠BDE=180°, ∴∠OCD+∠ODC=90°, ∵AC=x,BD=y, ∴OC=
??
2
+81
,OD=
??
2
+81
, ∵CD是圆O的切线, ∴CE=AC=x,DE=BD=y, ∴OC2+OD2=CD2 , 即x2+81+y2+81=(x+y)2 , 整理得2xy=162, ∴xy=81. /
27.【答案】证明(1)∵AC为直径,∴∠ABC=90°, ∵OD∥BC,∴∠ADO=∠ABC=90°, 在△AOD和△EOF中,
∠??????=∠??????
∠??????=∠??????
????=????
∴△AOD≌△EOF, ∴OD=OF, ∴∠ODF=∠OFD, ∵OD∥BC,∴∠FGC=∠ODF, 又∠GFC=∠OFD, ∴∠CFG=∠FGC, ∴FC=GC; (2)连接AE、EC, ∵OA=OE,∴∠OAE=∠OEA, ∵OD=OF,∴∠ODF=∠OFD, ∴∠OAE=∠OFD, ∴AE∥DG, ∵AC为直径,∴∠AEC=90°,又CF=CG, ∴CE是FG的垂直平分线, ∴△EFC≌△EGC, ∴∠EGC=∠EFC=90°, 又∠EDB=90°,∠ABC=90°, ∴四边形EDBG是矩形. /
28.【答案】解:应用:∵△ABC是等边三角形, ∴∠ABC=60°, ∵BF为角平分线, ∴∠PBE=30°, ∴PE=
1
2
PB, ∵BF是等边△ABC的角平分线, ∴BF⊥AC, ∵PF=
1
2
BF, ∴PE=PD=PF, ∴P是△ABC的内心; 探究:根据题意得: PD=PC=
1
2
AP, ∵sin??=
????
????
=
1
2
????
????
=
1
2
, ∴∠A是锐角, ∴∠A=30°.
29.【答案】解:过点C作CE⊥AD于点E, / 则AE=DE, ∵∠ACB=90°,AC=3,BC=4, ∴AB= /=5, ∵S△ABC= /AC?BC= /AB?CE, ∴CE= /= /= /, ∴AE= /= /, ∴AD=2AE= /.
30.【答案】(1)相切 (2)解:①存在 ∵PA=PB, ∴点P为∠AOB的平分线或反向延长线与⊙O的交点, 如图2, 当P点在优弧AB上时, 设⊙Q的半径为/, 若⊙Q与⊙O内切,可得2+(2-x)=2x,解得x=
4
3
, 若⊙Q与⊙O外切,可得2+(x+2)=2x,?解得x=4 , 当P点在劣弧AB上时, 同理可得:x=8
3
-12,x=8
3
+12 , 综上所述,存在⊙Q,半径可以为
4
3
,4 ,8
3
-12,8
3
+12; ②存在.作QH⊥PB于H,如图3, ∵PA⊥PB, ∴∠APB=90°, ∵⊙Q与射线PA.PB相切, ∴PQ平分∠APB, ∴∠QPH=45°, ∴△QHP为等腰直角三角形, ∴QH=PH, 在Rt△POA中,∠AOP=60°,OA=2, ∴OP=1, 设⊙Q的半径为r,即PH=QH=r,则OH=PH﹣OP=r﹣1, 在Rt△OQH中,OQ2=OH2+QH2=(r﹣1)2+r2, 若⊙Q与⊙O内切时,OQ=2﹣r,则(2﹣r)2=(r﹣1)2+r2,解得r1=1,r2=﹣3(舍去); 若⊙Q与⊙O外切时,OQ=2+r,则(2+r)2=(r﹣1)2+r2,解得r1=3+2
3
,r2=3-2
3
(舍去); 综上所述,存在⊙Q,其半径可以为1,3+2
3
. /.
