湘教版九年级下《第二章圆》单元检测试卷(含答案)
文档属性
| 名称 | 湘教版九年级下《第二章圆》单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 164.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-21 21:52:41 | ||
图片预览



文档简介
【专题突破训练】湘教版九年级数学下册 第二章 圆 单元检测试卷
一、单选题(共10题;共30分)
1.已知OA=5cm,以O为圆心,r为半径作⊙O.若点A在⊙O内,则r的值可以是( )
A.?3cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?5cm?????????????????????????????????????D.?6cm
2.已知⊙O的直径为4,点P到点O的距离为3,则下列对于点P与⊙O位置关系的说法正确的是( )
A.?在圆上????????????????????????????????/B.?在圆内????????????????????????????????/C.?在圆外????????????????????????????????/D.?不确定
3.如图,AB是?O的直径,点C在圆上,且∠??????=50°.则∠??????( ) /
A.?50°???????????????????????????????????????B.?40°???????????????????????????????????????C.?30°???????????????????????????????????????D.?20°
4.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5
3
,则∠B的度数是(??? ) /
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
5.如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论不一定成立的是(??? ) /
A.?∠COE=∠DOE????????????????????????/B.?CE=DE????????????????????????/C.?OE=BE????????????????????????/D.?弧BC=弧BD
6.在以AB为直径的⊙O中,AB=8,若OP=5,则点P与⊙O的位置关系是( )
A.?点P在⊙O内??????????????????????/B.?点P在⊙O上??????????????????????/C.?点P在⊙O外??????????????????????/D.?无法确定
7.边长为4cm的正方形ABCD绕它的顶点A旋转180°,顶点B所经过的路线长为( )cm.
A.?4π?????????????????????????????????????????B.?3π?????????????????????????????????????????C.?2π?????????????????????????????????????????D.?π
8.如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( ) /?
A.?8???????????????????????????????????????????/B.?6???????????????????????????????????????????/C.?4???????????????????????????????????????????/D.?2
9.正六边形的两条对边之间的距离是2
3
,则它的边长是(?? )
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.?
3
?????????????????????????????????????????D.?2
3
10.如图,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,那么⊙O的半径是(?? ) /
A.?5
2
cm???????????????????????????/B.?4
3
cm???????????????????????????/C.?3
5
cm???????????????????????????/D.?2
6
cm
二、填空题(共8题;共24分)
11.已知扇形的圆心角为120°,弧长为6π,则它的半径为________.
12.如图, ???? 是 ⊙?? 的直径, ?? 是 ⊙?? 上的点,过点 ?? 作 ⊙?? 的切线交 ???? 的延长线于点 ?? .若∠A=32°,则 ∠??= ________度./
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,CD=6,则BE=________. /
14.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为________. /
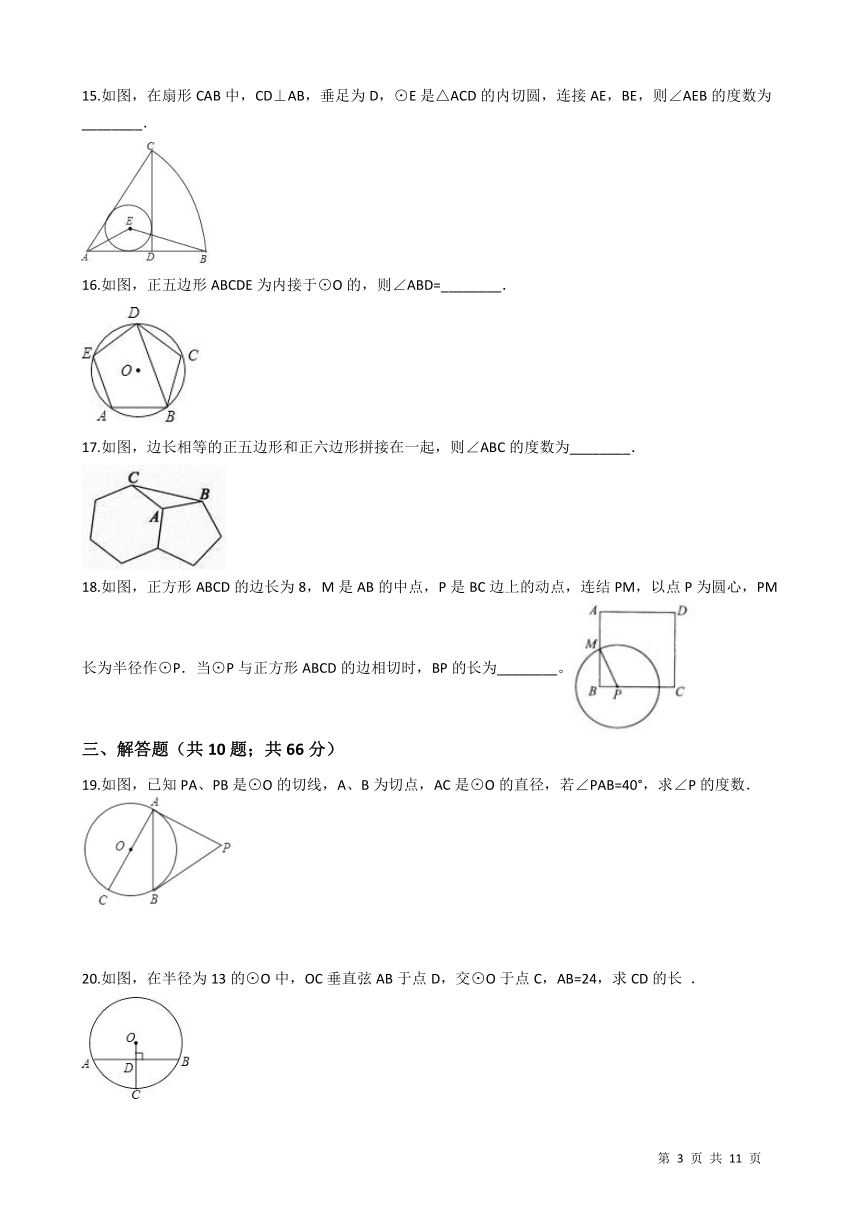
15.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为________. /
16.如图,正五边形ABCDE为内接于⊙O的,则∠ABD=________.
/
17.如图,边长相等的正五边形和正六边形拼接在一起,则∠ABC的度数为________.
/
18.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________。/
三、解答题(共10题;共66分)
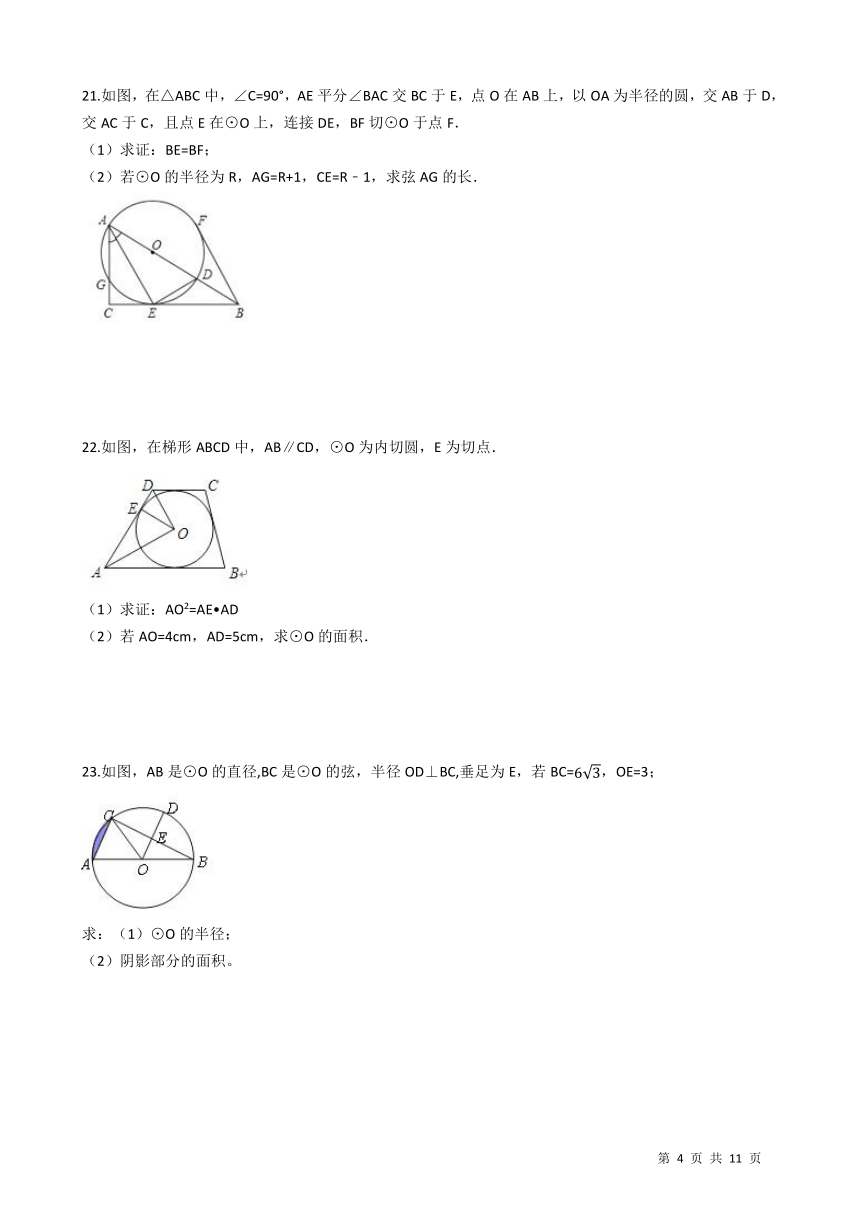
19.如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠PAB=40°,求∠P的度数. /
20.如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,求CD的长 . /
21.如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F. (1)求证:BE=BF; (2)若⊙O的半径为R,AG=R+1,CE=R﹣1,求弦AG的长. /
22.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点. /
(1)求证:AO2=AE?AD
(2)若AO=4cm,AD=5cm,求⊙O的面积.
23.如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=6
3
,OE=3; / 求:(1)⊙O的半径; (2)阴影部分的面积。
24.已知如图,⊙O的内接△ABC中,AB=AC,弦BD,CE分别∠ABC,∠ACB,且BE=BC,求证:五边形AEBCD是正五边形. /
25.如图, △ABC内接于⊙O, AD⊥BC于D, AE是⊙O的直径. 若AB=6, AC=8, AE=11, 求AD的长. /
26.如图,AB是⊙O的直径,C是⊙O上的一点,DA与⊙O相切于点A,DA=DC=
3
. [MISSING IMAGE: , ] (1)求证:DC是⊙O的切线; (2)若∠CAB=30°,求阴影部分的面积.
27.如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小/
28.如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=
5
,CD=2. / (1)求直径BC的长; (2)求弦AB的长.
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】B
10.【答案】C
二、填空题
11.【答案】9
12.【答案】26
13.【答案】1
14.【答案】5
15.【答案】135°
16.【答案】72°
17.【答案】24°
18.【答案】3或 4
3
三、解答题
19.【答案】解:∵PA和PB为切线 ,A,B是切点 ∴PA=PB ∴∠PBA=∠PAB=40° ∴∠P=180°-(∠PAB+∠PBA)=100°.
20.【答案】解:连接 O A , / ∵ ????⊥???? , ????=24 , ∴ ????=
1
2
????=12 , 在 ???????????? 中, ∵ ????=13 , ????=12 , ∴ ????=5 , ∴ ????=?????????=13?5=8
21.【答案】证明:(1)连接DG、OE,交于点H. ∵AE平分∠BAC交BC于E, ∴∠CAE=∠DAE, ∵OA=OE, ∴∠OAE=∠OEA, ∴∠CAE=∠OEA, ∴AC∥OE, ∴∠OEB=∠C=90°, ∴OE⊥BC, ∴BC是圆的切线, ∴BE=BF; (2)解:∵AB是直径, ∵∠AGD=90°, ∵∠C=90°, ∴GD∥BC, ∵OE⊥BC, ∴OE⊥GD, ∴GH=DH, ∵∠AGD=90°,∠C=90°,OE⊥BC, ∴四边形GCEH是矩形, ∴GH=CE=R﹣1, ∴GD=2(R﹣1)=2R﹣2, 在直角三角形AGD中,AG2+GD2=AD2 , 即(R+1)2+(2R﹣2)2=(2R)2 解得R1=5,R2=1(舍去), ∴AG=R+1=5+1=6; /
22.【答案】(1)证明:根据切线长定理可知: ∵∠OAE+∠ODA=
1
2
(∠BAD+∠ADC)=90°, ∴∠AOD=90°, ∵∠OAE=∠OAE,∠AOD=∠AEO=90°, ∴△AOE∽△ADO, ∴
????
????
=
????
????
即AO2=AE?AD (2)解:在Rt△AOD中, OD=
??
??
2
???
??
2
=3, ∵S△AOD=
1
2
×AD×EO=
1
2
×AO×OD 即5×EO=4×3, ∴EO=
12
5
, ∵OE是⊙O的半径, ∴S圆O=πr2=
144
25
π.
23.【答案】解:(1)∵BC是⊙O的弦,半径OD⊥BC,BC=6
3
,∴CE=
1
2
BC=3
3
. ∴在Rt△COE中,由勾股定理得,????=
??
??
2
???
??
2
=
3
3
2
+
3
2
=6, ∴⊙O的半径是6. (2)∵在Rt△COE中,∠CEO=90°,CO=2OE,∴∠ECO=30°. ∵AB是⊙O的直径,∴∠ACB=90°.∴∠ACO=60°. ∵OA=OC,∴△ACO是等边三角形.∴∠AOC=60°. ∴S阴影=S扇形ACO-S△AOC=
60·π·
6
2
360
?
1
2
·6·6·
3
2
=6π?9
3
. 答:阴影部分的面积是6π?9
3
.
24.【答案】证明:∵AB=AC, ∴∠ABC=∠ACB, ∵弦BD,CE分别平分∠ABC,∠ACB, ∴∠ABD=∠DBC=∠ECB=∠ACE, ∵BE=BC, ∴
????
∧
=
????
∧
∴∠BEC=∠BCE, ∵∠BCA=∠BEC, ∴∠ABD=∠DBC=∠ECB=∠ACE=∠BAC, ∴
????
∧
=
????
∧
=
????
∧
=
????
∧
=
????
∧
, ∴五边形AEBCD是正五边形. /
25.【答案】解:连接CE,则∠E=∠B, / ∵AE是⊙O的直径, ∴∠ACE=90°, 又∵AD⊥BC, ∴∠ACE=∠ADB=90°, ∴△ACE∽△ADB, ∴
????
????
=
????
????
, 即
11
6
=
8
????
, 解得AD=
48
11
26.【答案】
27.【答案】解:如图:作点C关于AB的对称点M,点E关于AB的对称点N,连结CM、FM,设CM交AB于点Q, 依题可得AB⊥CM,CQ=MQ, ∴∠CFA=∠AFM, 又∵∠CFA=∠DFB, ∴∠AFM=∠DFB, ∴D、F、M三点共线, 同理可得D、G、N三点共线, 又∵弧AC=60°,弧BE=20°, ∴弧AM=弧AC=60°,弧BN=弧BE=20°, ∴弧MN=180°-60°-20°=100°, ∴∠FDG=
1
2
×100°=50°. /
28.【答案】解:(1)∵BC是半圆O的直径,∴∠BDC=900. ∵CE=
5
,CD=2,∴根据勾股定理,得DE=1. ∵D是弧AC的中点,∴AD=CD=2. 易证△ADE∽△BCE,∴
????
????
=
????
????
,即
2
????
=
1
5
,解得BC=2
5
. (2) 易证△ABE∽△DCE, ∴
????
????
=
????
????
=
1
2
. 设AE=x , 则AB=2x,AC=x+
5
, ∵AB2+AC2=BC2,∴(2x)2+(x+
5
)2=(2
5
)2 , 解得x=
?2
5
±8
5
10
. ∵x>0,∴x=
3
5
5
.∴AB=2x=
6
5
5
.
一、单选题(共10题;共30分)
1.已知OA=5cm,以O为圆心,r为半径作⊙O.若点A在⊙O内,则r的值可以是( )
A.?3cm?????????????????????????????????????B.?4cm?????????????????????????????????????C.?5cm?????????????????????????????????????D.?6cm
2.已知⊙O的直径为4,点P到点O的距离为3,则下列对于点P与⊙O位置关系的说法正确的是( )
A.?在圆上????????????????????????????????/B.?在圆内????????????????????????????????/C.?在圆外????????????????????????????????/D.?不确定
3.如图,AB是?O的直径,点C在圆上,且∠??????=50°.则∠??????( ) /
A.?50°???????????????????????????????????????B.?40°???????????????????????????????????????C.?30°???????????????????????????????????????D.?20°
4.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5
3
,则∠B的度数是(??? ) /
A.?30°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
5.如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论不一定成立的是(??? ) /
A.?∠COE=∠DOE????????????????????????/B.?CE=DE????????????????????????/C.?OE=BE????????????????????????/D.?弧BC=弧BD
6.在以AB为直径的⊙O中,AB=8,若OP=5,则点P与⊙O的位置关系是( )
A.?点P在⊙O内??????????????????????/B.?点P在⊙O上??????????????????????/C.?点P在⊙O外??????????????????????/D.?无法确定
7.边长为4cm的正方形ABCD绕它的顶点A旋转180°,顶点B所经过的路线长为( )cm.
A.?4π?????????????????????????????????????????B.?3π?????????????????????????????????????????C.?2π?????????????????????????????????????????D.?π
8.如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( ) /?
A.?8???????????????????????????????????????????/B.?6???????????????????????????????????????????/C.?4???????????????????????????????????????????/D.?2
9.正六边形的两条对边之间的距离是2
3
,则它的边长是(?? )
A.?1?????????????????????????????????????????B.?2?????????????????????????????????????????C.?
3
?????????????????????????????????????????D.?2
3
10.如图,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,那么⊙O的半径是(?? ) /
A.?5
2
cm???????????????????????????/B.?4
3
cm???????????????????????????/C.?3
5
cm???????????????????????????/D.?2
6
cm
二、填空题(共8题;共24分)
11.已知扇形的圆心角为120°,弧长为6π,则它的半径为________.
12.如图, ???? 是 ⊙?? 的直径, ?? 是 ⊙?? 上的点,过点 ?? 作 ⊙?? 的切线交 ???? 的延长线于点 ?? .若∠A=32°,则 ∠??= ________度./
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,CD=6,则BE=________. /
14.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为________. /
15.如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB的度数为________. /
16.如图,正五边形ABCDE为内接于⊙O的,则∠ABD=________.
/
17.如图,边长相等的正五边形和正六边形拼接在一起,则∠ABC的度数为________.
/
18.如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________。/
三、解答题(共10题;共66分)
19.如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,若∠PAB=40°,求∠P的度数. /
20.如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,求CD的长 . /
21.如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F. (1)求证:BE=BF; (2)若⊙O的半径为R,AG=R+1,CE=R﹣1,求弦AG的长. /
22.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点. /
(1)求证:AO2=AE?AD
(2)若AO=4cm,AD=5cm,求⊙O的面积.
23.如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=6
3
,OE=3; / 求:(1)⊙O的半径; (2)阴影部分的面积。
24.已知如图,⊙O的内接△ABC中,AB=AC,弦BD,CE分别∠ABC,∠ACB,且BE=BC,求证:五边形AEBCD是正五边形. /
25.如图, △ABC内接于⊙O, AD⊥BC于D, AE是⊙O的直径. 若AB=6, AC=8, AE=11, 求AD的长. /
26.如图,AB是⊙O的直径,C是⊙O上的一点,DA与⊙O相切于点A,DA=DC=
3
. [MISSING IMAGE: , ] (1)求证:DC是⊙O的切线; (2)若∠CAB=30°,求阴影部分的面积.
27.如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小/
28.如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE=
5
,CD=2. / (1)求直径BC的长; (2)求弦AB的长.
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】B
10.【答案】C
二、填空题
11.【答案】9
12.【答案】26
13.【答案】1
14.【答案】5
15.【答案】135°
16.【答案】72°
17.【答案】24°
18.【答案】3或 4
3
三、解答题
19.【答案】解:∵PA和PB为切线 ,A,B是切点 ∴PA=PB ∴∠PBA=∠PAB=40° ∴∠P=180°-(∠PAB+∠PBA)=100°.
20.【答案】解:连接 O A , / ∵ ????⊥???? , ????=24 , ∴ ????=
1
2
????=12 , 在 ???????????? 中, ∵ ????=13 , ????=12 , ∴ ????=5 , ∴ ????=?????????=13?5=8
21.【答案】证明:(1)连接DG、OE,交于点H. ∵AE平分∠BAC交BC于E, ∴∠CAE=∠DAE, ∵OA=OE, ∴∠OAE=∠OEA, ∴∠CAE=∠OEA, ∴AC∥OE, ∴∠OEB=∠C=90°, ∴OE⊥BC, ∴BC是圆的切线, ∴BE=BF; (2)解:∵AB是直径, ∵∠AGD=90°, ∵∠C=90°, ∴GD∥BC, ∵OE⊥BC, ∴OE⊥GD, ∴GH=DH, ∵∠AGD=90°,∠C=90°,OE⊥BC, ∴四边形GCEH是矩形, ∴GH=CE=R﹣1, ∴GD=2(R﹣1)=2R﹣2, 在直角三角形AGD中,AG2+GD2=AD2 , 即(R+1)2+(2R﹣2)2=(2R)2 解得R1=5,R2=1(舍去), ∴AG=R+1=5+1=6; /
22.【答案】(1)证明:根据切线长定理可知: ∵∠OAE+∠ODA=
1
2
(∠BAD+∠ADC)=90°, ∴∠AOD=90°, ∵∠OAE=∠OAE,∠AOD=∠AEO=90°, ∴△AOE∽△ADO, ∴
????
????
=
????
????
即AO2=AE?AD (2)解:在Rt△AOD中, OD=
??
??
2
???
??
2
=3, ∵S△AOD=
1
2
×AD×EO=
1
2
×AO×OD 即5×EO=4×3, ∴EO=
12
5
, ∵OE是⊙O的半径, ∴S圆O=πr2=
144
25
π.
23.【答案】解:(1)∵BC是⊙O的弦,半径OD⊥BC,BC=6
3
,∴CE=
1
2
BC=3
3
. ∴在Rt△COE中,由勾股定理得,????=
??
??
2
???
??
2
=
3
3
2
+
3
2
=6, ∴⊙O的半径是6. (2)∵在Rt△COE中,∠CEO=90°,CO=2OE,∴∠ECO=30°. ∵AB是⊙O的直径,∴∠ACB=90°.∴∠ACO=60°. ∵OA=OC,∴△ACO是等边三角形.∴∠AOC=60°. ∴S阴影=S扇形ACO-S△AOC=
60·π·
6
2
360
?
1
2
·6·6·
3
2
=6π?9
3
. 答:阴影部分的面积是6π?9
3
.
24.【答案】证明:∵AB=AC, ∴∠ABC=∠ACB, ∵弦BD,CE分别平分∠ABC,∠ACB, ∴∠ABD=∠DBC=∠ECB=∠ACE, ∵BE=BC, ∴
????
∧
=
????
∧
∴∠BEC=∠BCE, ∵∠BCA=∠BEC, ∴∠ABD=∠DBC=∠ECB=∠ACE=∠BAC, ∴
????
∧
=
????
∧
=
????
∧
=
????
∧
=
????
∧
, ∴五边形AEBCD是正五边形. /
25.【答案】解:连接CE,则∠E=∠B, / ∵AE是⊙O的直径, ∴∠ACE=90°, 又∵AD⊥BC, ∴∠ACE=∠ADB=90°, ∴△ACE∽△ADB, ∴
????
????
=
????
????
, 即
11
6
=
8
????
, 解得AD=
48
11
26.【答案】
27.【答案】解:如图:作点C关于AB的对称点M,点E关于AB的对称点N,连结CM、FM,设CM交AB于点Q, 依题可得AB⊥CM,CQ=MQ, ∴∠CFA=∠AFM, 又∵∠CFA=∠DFB, ∴∠AFM=∠DFB, ∴D、F、M三点共线, 同理可得D、G、N三点共线, 又∵弧AC=60°,弧BE=20°, ∴弧AM=弧AC=60°,弧BN=弧BE=20°, ∴弧MN=180°-60°-20°=100°, ∴∠FDG=
1
2
×100°=50°. /
28.【答案】解:(1)∵BC是半圆O的直径,∴∠BDC=900. ∵CE=
5
,CD=2,∴根据勾股定理,得DE=1. ∵D是弧AC的中点,∴AD=CD=2. 易证△ADE∽△BCE,∴
????
????
=
????
????
,即
2
????
=
1
5
,解得BC=2
5
. (2) 易证△ABE∽△DCE, ∴
????
????
=
????
????
=
1
2
. 设AE=x , 则AB=2x,AC=x+
5
, ∵AB2+AC2=BC2,∴(2x)2+(x+
5
)2=(2
5
)2 , 解得x=
?2
5
±8
5
10
. ∵x>0,∴x=
3
5
5
.∴AB=2x=
6
5
5
.
