江苏省高邮市朝阳中学2018-2019年八年级数学5.2平面直角坐标系教案
文档属性
| 名称 | 江苏省高邮市朝阳中学2018-2019年八年级数学5.2平面直角坐标系教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-24 00:00:00 | ||
图片预览


文档简介
5.2《平面直角坐标系》教案
教学目标
1.认识平面直角坐标系,知道点的坐标及象限的含义.
2.能根据点的坐标指出点的位置,会由点的位置写出点的坐标.在给定的平面直角坐标系中,会根据坐标描出点的位置.
教学重点
能根据点的坐标指出点的位置.
教学难点
会由点的位置写出点的坐标.
教学过程
一、回顾旧知:
1、通过上一节的学习,你已经掌握了几种确定物体位置的方法?
2、_________________________________________是数轴.数轴上的点与_________________一一对应.
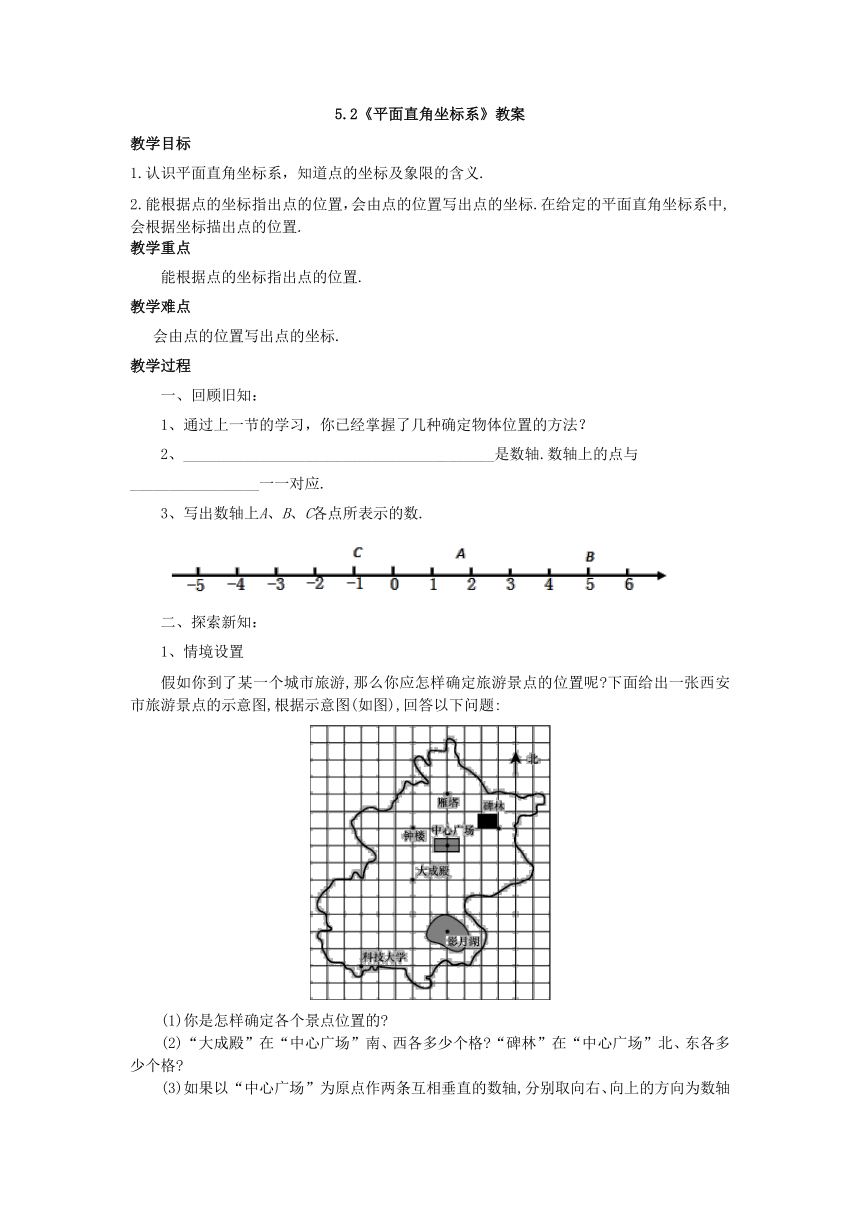
3、写出数轴上A、B、C各点所表示的数.
二、探索新知:
1、情境设置
假如你到了某一个城市旅游,那么你应怎样确定旅游景点的位置呢?下面给出一张西安市旅游景点的示意图,根据示意图(如图),回答以下问题:
(1)你是怎样确定各个景点位置的?
(2)“大成殿”在“中心广场”南、西各多少个格?“碑林”在“中心广场”北、东各多少个格?
(3)如果以“中心广场”为原点作两条互相垂直的数轴,分别取向右、向上的方向为数轴的正方向,一个方格的边长看作一个单位长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢?
合作探究
1.平面直角坐标系、横轴、纵轴、横坐标、纵坐标、原点的定义和象限的划分.
在了解有关平面直角坐标系的知识后,再返回刚才讨论的问题.
结论:如果以“中心广场”为原点作两条互相垂直的数轴,分别取向右、向上的方向为数轴的正方向,一个方格的边长看作一个单位长度,则“碑林”的位置是(3,1),“大成殿”的位置是(-2,-2).
问题:在(3)的条件下,你能把其他景点的位置表示出来吗?
结论:能,钟楼的位置是(-2,1),雁塔的位置是(0,3),影月湖的位置是(0,-5),科技大学的位置是(-5,-7).
小结归纳:
平面上有公共原点且互相垂直的2条数轴构成平面直角坐标系,简称为直角坐标系.水平方向的数轴称为x轴或横轴,竖直方向的数轴称为y轴或纵轴,它们统称为坐标轴.公共原点O称为坐标原点.
2条坐标轴将平面分成4个区域称为象限,按逆时针顺序分别记为:第一象限、第二象限、第三象限、第四象限.
注意:坐标轴上的点不属于任何象限.
例1:写出图中多边形ABCDEF各顶点的坐标.此图中各顶点的坐标是否永远不变?你能举个例子吗?
[解析] 多边形ABCDEF各顶点的坐标分别为A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3).不是.当坐标轴的位置发生变动时,各点的坐标相应地变化.若以线段BC所在的直线为x轴,纵轴(y轴)位置不变,如图,
则六个顶点的坐标分别为A(-2,3),B(0,0),C(3,0),D(4,3),E(3,6),F(0,6).再思考这个结论是否是永恒的.
结论:不是.还能再改变坐标轴的位置,得出不同的坐标.继续进行坐标轴的变换,总结一下共有多少种不同的变换方式.
练习:如图,确定点A,B,C,D,E,F,G的坐标.
[解析] 点A(-1,-1),点B(0,-3),点C(2,-5),点D(4,-1),点E(3,2),点F(-2,3),点G(2,-2).
例2:在图中的平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来,观察所得的图形,看一看像什么?
(1)(0,0),(1,3),(2,0),(3,3),(4,0);
(2)(0,3),(1,0),(2,3),(3,0),(4,3).
归纳总结:在平面直角坐标系中,通过找点、连线、观察,确定图形的大致形状,进一步掌握平面直角坐标系的基本内容
三、课内反馈:
1、已知点A的坐标是(-2,3),则它在第几象限.
2、已知P点坐标为(2a+1,a-3)
(1)点P在x轴上,则a=________;②点P在y轴上,则a=______.
(2)点P到x轴距离为2,则点P到原点的距离为_______.
3、当x=_____时,点M(2x-4,6)在y轴上.
4、已知点P的坐标是(4,-6),则这个点到x轴的距离是_______.
5、若点A(a-1,a)在第二象限,则点B(a,1-a)在第________象限.
6、若某点向右平移2个单位,再向下平移3个单位后,所得的点是坐标原点,则这点的坐标是_________.
7、若点P(x,y)在第四象限,到x轴距离为4,到原点距离为5,求P点的坐标.
四、课堂小结:本节课你有哪些收获?
教学反思:引导学生去学习找点的位置和它们的坐标之间的关系,形成数形结合的思想,用数字特征去描述它们之间的关系.
课后作业:;
1、两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴叫做或,铅直的数轴叫做 或,它们的公共原点O称为.
2、对于平面内任意一点,过点分别向轴、轴作垂线,垂足在轴、轴上对应的数,分别叫做点的______、_______,有序数对(,)叫做点的坐标.
3、各个象限内的点的坐标特征:
第一象限( , ) 第二象限( , ) 第三象限( , ) 第四象限( , )
4、如果点P(a+3,2a+4)在y轴上,则点P的坐标是()
A.(-2,0) B.(0,-2) C.(0,1) D.(1,0)
5、 已知点A(-3,2),点B(1,4),
⑴ 若CA平行于x轴,BC平行于y轴,则点C的坐标是;
⑵ 若CA平行于y轴,BC平行于x轴,则点C的坐标是.
6、如果点M到x轴和y轴的距离相等,则点M的横、纵坐标的关系是( )
A. 相等 B. 互为相反数 C. 互为倒数 D. 相等或互为相反数
7、若点P(在第一象限内两坐标轴夹角的平分线上,则若点Q(在第四象限内两坐标轴夹角的平分线上,则n=_______.
8、如果点P(在轴上方,轴的右侧,且该点到轴与到轴的距离相等,则的值为_______.
9、在平面直角坐标系中有A、B两点,若以B点为原点建立直角坐标系,则A点的坐标为若以A点为原点建立直角坐标系(两直角坐标系x轴、y轴方向一致),则B点的坐标是( )
A. B.C. D.
10、如图,△AOB为正三角形,点A,B的坐标分别为(2,a),(b,0),求a,b的值及△AOB的面积.
11、如图,三角形ABC中,A,B两点坐标分别为A(3,3),B(4,0),求出三角形ABC面积.
教学目标
1.认识平面直角坐标系,知道点的坐标及象限的含义.
2.能根据点的坐标指出点的位置,会由点的位置写出点的坐标.在给定的平面直角坐标系中,会根据坐标描出点的位置.
教学重点
能根据点的坐标指出点的位置.
教学难点
会由点的位置写出点的坐标.
教学过程
一、回顾旧知:
1、通过上一节的学习,你已经掌握了几种确定物体位置的方法?
2、_________________________________________是数轴.数轴上的点与_________________一一对应.
3、写出数轴上A、B、C各点所表示的数.
二、探索新知:
1、情境设置
假如你到了某一个城市旅游,那么你应怎样确定旅游景点的位置呢?下面给出一张西安市旅游景点的示意图,根据示意图(如图),回答以下问题:
(1)你是怎样确定各个景点位置的?
(2)“大成殿”在“中心广场”南、西各多少个格?“碑林”在“中心广场”北、东各多少个格?
(3)如果以“中心广场”为原点作两条互相垂直的数轴,分别取向右、向上的方向为数轴的正方向,一个方格的边长看作一个单位长度,那么你能表示“碑林”的位置吗?“大成殿”的位置呢?
合作探究
1.平面直角坐标系、横轴、纵轴、横坐标、纵坐标、原点的定义和象限的划分.
在了解有关平面直角坐标系的知识后,再返回刚才讨论的问题.
结论:如果以“中心广场”为原点作两条互相垂直的数轴,分别取向右、向上的方向为数轴的正方向,一个方格的边长看作一个单位长度,则“碑林”的位置是(3,1),“大成殿”的位置是(-2,-2).
问题:在(3)的条件下,你能把其他景点的位置表示出来吗?
结论:能,钟楼的位置是(-2,1),雁塔的位置是(0,3),影月湖的位置是(0,-5),科技大学的位置是(-5,-7).
小结归纳:
平面上有公共原点且互相垂直的2条数轴构成平面直角坐标系,简称为直角坐标系.水平方向的数轴称为x轴或横轴,竖直方向的数轴称为y轴或纵轴,它们统称为坐标轴.公共原点O称为坐标原点.
2条坐标轴将平面分成4个区域称为象限,按逆时针顺序分别记为:第一象限、第二象限、第三象限、第四象限.
注意:坐标轴上的点不属于任何象限.
例1:写出图中多边形ABCDEF各顶点的坐标.此图中各顶点的坐标是否永远不变?你能举个例子吗?
[解析] 多边形ABCDEF各顶点的坐标分别为A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3).不是.当坐标轴的位置发生变动时,各点的坐标相应地变化.若以线段BC所在的直线为x轴,纵轴(y轴)位置不变,如图,
则六个顶点的坐标分别为A(-2,3),B(0,0),C(3,0),D(4,3),E(3,6),F(0,6).再思考这个结论是否是永恒的.
结论:不是.还能再改变坐标轴的位置,得出不同的坐标.继续进行坐标轴的变换,总结一下共有多少种不同的变换方式.
练习:如图,确定点A,B,C,D,E,F,G的坐标.
[解析] 点A(-1,-1),点B(0,-3),点C(2,-5),点D(4,-1),点E(3,2),点F(-2,3),点G(2,-2).
例2:在图中的平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来,观察所得的图形,看一看像什么?
(1)(0,0),(1,3),(2,0),(3,3),(4,0);
(2)(0,3),(1,0),(2,3),(3,0),(4,3).
归纳总结:在平面直角坐标系中,通过找点、连线、观察,确定图形的大致形状,进一步掌握平面直角坐标系的基本内容
三、课内反馈:
1、已知点A的坐标是(-2,3),则它在第几象限.
2、已知P点坐标为(2a+1,a-3)
(1)点P在x轴上,则a=________;②点P在y轴上,则a=______.
(2)点P到x轴距离为2,则点P到原点的距离为_______.
3、当x=_____时,点M(2x-4,6)在y轴上.
4、已知点P的坐标是(4,-6),则这个点到x轴的距离是_______.
5、若点A(a-1,a)在第二象限,则点B(a,1-a)在第________象限.
6、若某点向右平移2个单位,再向下平移3个单位后,所得的点是坐标原点,则这点的坐标是_________.
7、若点P(x,y)在第四象限,到x轴距离为4,到原点距离为5,求P点的坐标.
四、课堂小结:本节课你有哪些收获?
教学反思:引导学生去学习找点的位置和它们的坐标之间的关系,形成数形结合的思想,用数字特征去描述它们之间的关系.
课后作业:;
1、两条数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向.水平的数轴叫做或,铅直的数轴叫做 或,它们的公共原点O称为.
2、对于平面内任意一点,过点分别向轴、轴作垂线,垂足在轴、轴上对应的数,分别叫做点的______、_______,有序数对(,)叫做点的坐标.
3、各个象限内的点的坐标特征:
第一象限( , ) 第二象限( , ) 第三象限( , ) 第四象限( , )
4、如果点P(a+3,2a+4)在y轴上,则点P的坐标是()
A.(-2,0) B.(0,-2) C.(0,1) D.(1,0)
5、 已知点A(-3,2),点B(1,4),
⑴ 若CA平行于x轴,BC平行于y轴,则点C的坐标是;
⑵ 若CA平行于y轴,BC平行于x轴,则点C的坐标是.
6、如果点M到x轴和y轴的距离相等,则点M的横、纵坐标的关系是( )
A. 相等 B. 互为相反数 C. 互为倒数 D. 相等或互为相反数
7、若点P(在第一象限内两坐标轴夹角的平分线上,则若点Q(在第四象限内两坐标轴夹角的平分线上,则n=_______.
8、如果点P(在轴上方,轴的右侧,且该点到轴与到轴的距离相等,则的值为_______.
9、在平面直角坐标系中有A、B两点,若以B点为原点建立直角坐标系,则A点的坐标为若以A点为原点建立直角坐标系(两直角坐标系x轴、y轴方向一致),则B点的坐标是( )
A. B.C. D.
10、如图,△AOB为正三角形,点A,B的坐标分别为(2,a),(b,0),求a,b的值及△AOB的面积.
11、如图,三角形ABC中,A,B两点坐标分别为A(3,3),B(4,0),求出三角形ABC面积.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
