2018年秋季学期期末复习专用:北师大版七年级数学第四章《基本平面图形》单元检测试题及答案解析
文档属性
| 名称 | 2018年秋季学期期末复习专用:北师大版七年级数学第四章《基本平面图形》单元检测试题及答案解析 |  | |
| 格式 | zip | ||
| 文件大小 | 240.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-24 08:58:51 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
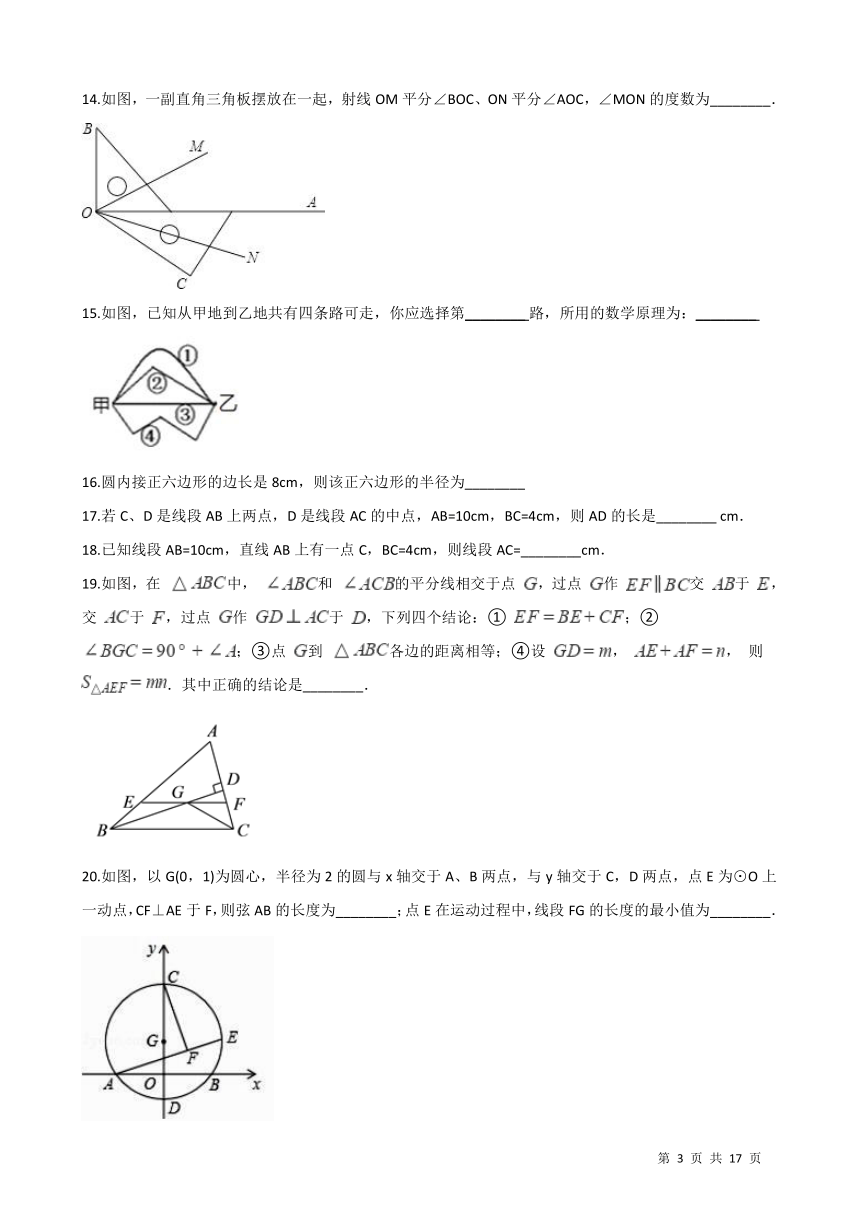
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
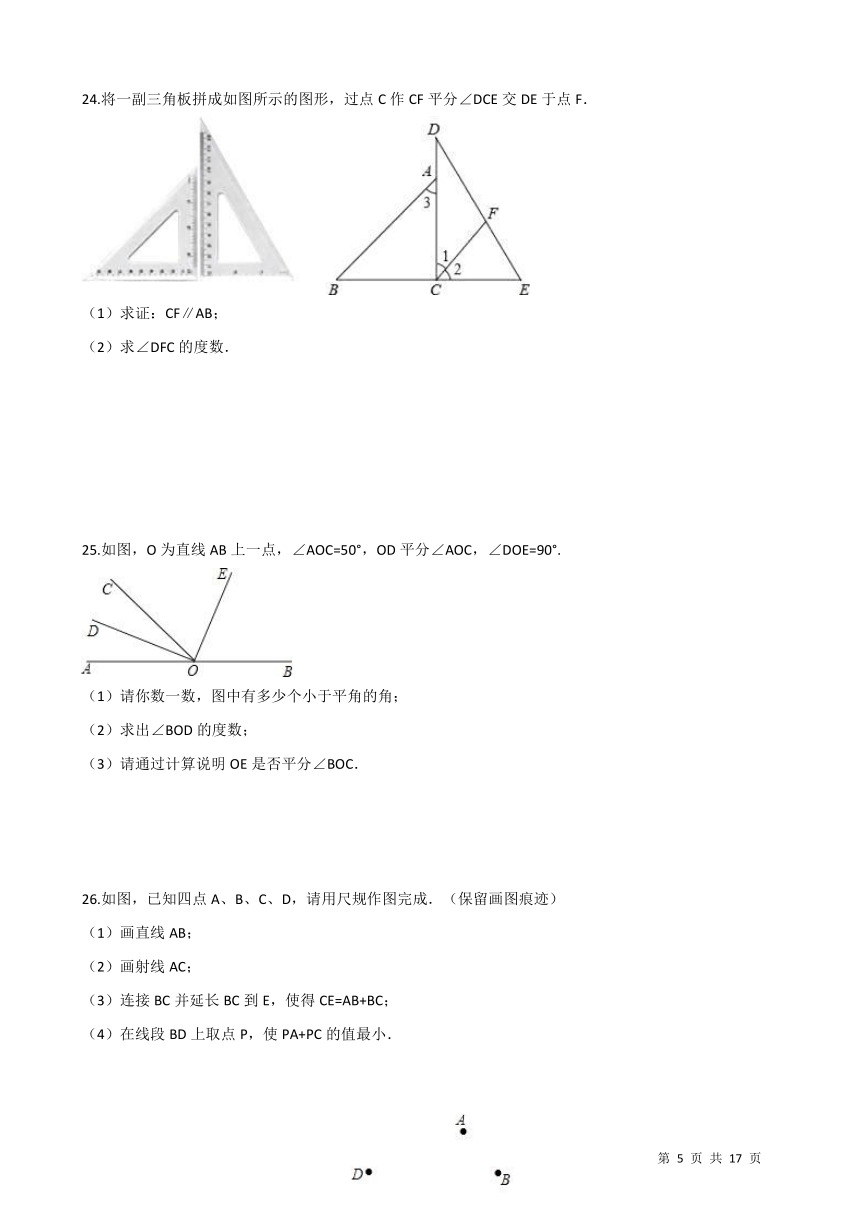
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大七年级数学第四章《基本平面图形》单元检测试题及答案解析
一、单选题(共10题;共20分)
1.钟表在3点半时,它的时针与分针所成锐角是(????)
A.?70 ??????????????????????????????????????B.?85 ??????????????????????????????????????C.?75 ??????????????????????????????????????D.?90 ?
2.由上饶到南昌的某一次列车,运行途中停靠的车站依次是:上饶﹣横峰﹣弋阳﹣贵溪﹣鹰潭﹣余江﹣东乡﹣莲塘﹣南昌,那么要为这次列车制作的火车票有(?? )
A.?9种?????????????????????????????????????B.?18种?????????????????????????????????????C.?36种?????????????????????????????????????D.?72种
3.下列说法:①两条直线最多有一个公共点,②两条直线可能有无数个公共点,③两条线段可能有无数个公共点,④一条直线和一条线段可能有无数个公共点,其中正确的个数为( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.下列说法正确的是(?? )
A.最小的有理数是0 B.射线OM的长度是5cm
C.两数相加,和一定大于任何一个加数 D.两点确定一条直线
5.已知∠AOB=50°,∠COB=30°,则∠AOC等于( )
A.?80°?????????????????????????????????B.?20°?????????????????????????????????C.?80°或20°?????????????????????????????????D.?无法确定
6.如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE等于( )
A.?18°???????????????????????????????????????B.?36°???????????????????????????????????????C.?45°???????????????????????????????????????D.?54°
7.下面表示∠ABC的图是(?? )
A.
B.
C.
D.
8.如图,量一量线段AB,BC,CA的长度,就能得到结论(?? )
A.?AB=BC+CA??????????????????B.?AB<BC+CA??????????????????C.?AB<|CA﹣BC|??????????????????D.?AB=|CA﹣BC|
9.如图,在直角△ABC中,∠C=90°,AD平分∠BAC,∠BAD=20°,则∠B的度数为(?? )
A.?40°???????????????????????????????????????B.?30°???????????????????????????????????????C.?60°???????????????????????????????????????D.?50°
10.下列语句,正确的是(? ).
A.?直线可表示一个平角;???????????????????????????????????B.?平角的两边向左右无限延伸;
C.?延长线段AB至点C,则∠ACB=180°;????????????D.?在一条直线上顺次取三点A、B、C,则∠ABC=180°
二、填空题(共10题;共24分)
11.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因________.
12.如图,正六边形ABCDEF的边长为2cm,点P为六边形内任一点.则点P到各边距离之和为________cm.
13.21°17′×5=________.
14.如图,一副直角三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC,∠MON的度数为________.
15.如图,已知从甲地到乙地共有四条路可走,你应选择第________?路,所用的数学原理为:________?
16.圆内接正六边形的边长是8cm,则该正六边形的半径为________
17.若C、D是线段AB上两点,D是线段AC的中点,AB=10cm,BC=4cm,则AD的长是________?cm.
18.已知线段AB=10cm,直线AB上有一点C,BC=4cm,则线段AC=________cm.
19.如图,在 中, 和 的平分线相交于点 ,过点 作 交 于 ,交 于 ,过点 作 于 ,下列四个结论:① ;② ;③点 到 各边的距离相等;④设 , , 则 .其中正确的结论是________.
20.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.
三、作图题(共2题;共10分)
21.如图,A、B、C三点不在同一条直线上,按要求画图:
( 1 )画直线AB;(2)画射线BC;(3)画线段CA.
22.已知四点A,B,C,D.根据下列语句,画出图形
①画直线AB;
②连接AC,BD,相交于点O;
③画射线AD,BC,交于点P.
四、综合题(共5题;共46分)
23.如图,直线AB与CD相交于点O, .
(1)如图1,若OC平分 ,求 的度数;
(2)如图2,若 ,且OM平分 ,求 的度数.
24.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
25.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
26.如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得CE=AB+BC;
(4)在线段BD上取点P,使PA+PC的值最小.
27.如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后,OM恰好平分∠BOC.①求t的值;②此时ON是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠MON?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠MOB?请画图并说明理由
答案解析部分
一、单选题
1.【答案】C
【解析】
∵3点半时,时针指向3和4中间,分针指向6.
钟表12个数字,每相邻两个数字之间的夹角为30°,半个格是15°,
∴3点半时,分针与时针的夹角正好是30°×2+15°=75度.
故选C.
2.【答案】C
【解析】解:每两站点都要设火车票,所以从一个城市出发到其他8个城市有8种车票,
但是已知中是由上饶到南昌的某一次列车,运行途中停靠的车站依次是:上饶﹣横峰﹣弋阳﹣贵溪﹣鹰潭﹣余江﹣东乡﹣莲塘﹣南昌,故没有往返车票,是单程车票,
所以要为这次列车制作的火车票有 ×8×9=36(种).
故选:C.
每两站点都要设火车票,从一个城市出发到其他8个城市有8种车票,进而得出答案.
3.【答案】C
【解析】解:①两条直线最多有一个公共点,错误;
②两条直线可能有无数个公共点,正确;
③两条线段可能有无数个公共点,正确;
④一条直线和一条线段可能有无数个公共点,正确.
故选C
根据直线、线段的相交的交点个数进行判断即可.
4.【答案】D
【解析】解:A、没有最小的有理数,故A不符合题意;
B、射线没有长度,故B不符合题意;
C、两个负数相加和小于任何一个加数,故C不符合题意;
D、两点确定一条直线,故D符合题意;
故选:D.
根据有理数的意义,有理数的加法,直线的性质,射线的定义,可得答案.
5.【答案】C
【解析】解:①如图1,OC在∠AOB内,
∵∠AOB=50°,∠COB=30°,
∴∠AOC=∠AOB﹣∠COB=50°﹣30°=20°;
②如图2,OC在∠AOB外,
∵∠AOB=50°,∠COB=30°,
∴∠AOC=∠AOB+∠COB=50°+30°=80°;
综上所述,∠AOC的度数是20°或80°.
故选:C.
解答此题的关键是明确此题射线OC的位置,有2种可能,然后根据图形和∠AOB=50°,即可求出∠AOC的度数.
6.【答案】A
【解析】解:∵AB∥CD,
∴∠BCD=∠B=36°,
∵CE平分∠BCD,
∴∠DC=18°
故选:A.
根据两直线平行,内错角相等可得∠BCD=∠B,再根据角平分线的定义求出∠DCE,从而求解.本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.
7.【答案】C
【解析】解:A、有四个小于平角的角,没有∠ABC,故错误;
B、用三个大写字母表示角,表示角顶点的字母在中间,应为∠BCA,故错误;
C、用三个大写字母表示角,表示角顶点的字母在中间,应为∠ABC,故正确;
D、用三个大写字母表示角,表示角顶点的字母在中间,应为∠BAC,故错误.
故选:C.
根据角的概念,对选项进行一一分析,排除错误答案.
8.【答案】B
【解析】解:根据两边之和大于第三边可得:BC+CA>AB, 故可得B正确.
故选B.
根据三角形的三边关系:两边之和大于第三边即可得出答案.
9.【答案】D
【解析】分析】利用角平分线的性质计算.
∵AD的平分∠BAC,∠BAD=20°
∴∠CAB=40°
又∵∠C=90°
∴∠B=50°
故选D.
【点评】此题综合考查角平分线,直角三角形的两锐角互余.
10.【答案】D
【解析】A. 一个角由有公共端点的两射线组成,一个平角的两边在一条直线上,则一条直线不是一个平角,所以错误;B.角的两边是射线,射线是无限长的,不能说无限延伸射线,故说法错误;? C.角的两边应该是射线,延长线段AB至点C,AB和BC都是线段,故错误;?? D . 在一条直线上顺次取三点A、B、C,则∠ABC是平角,等于180°,正确;故答案选D.
根据角的定义意义进行分析,然后排出错误的答案.
二、填空题
11.【答案】两点之间线段最短
【解析】解:为抄近路践踏草坪原因是:两点之间线段最短.
故答案为:两点之间线段最短.
为抄近路践踏草坪原因是:两点之间线段最短.
12.【答案】18
【解析】解:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=2×2×=6,
∴点P到各边距离之和为3BD=3×6=18.
故答案为:18.
过P作AB的垂线,交AB、DE分别为H、K,连接BD,由正六边形的性质可知AB∥DE,AF∥CD,BC∥EF,故HK⊥DE,过C作CG⊥BD,由等腰三角形的性质及正六边形的内角和定理可知,DB⊥AB⊥DE,再由锐角三角函数的定义可求出BG的长,进而可求出BD的长,由正六边形的性质可知点P到AF与CD的距离和及P到EF、BC的距离和均为BD的长,故可得出结论.
13.【答案】106°25′
【解析】解:21°17′×5=105°85′=106°25′.
故答案为:106°25′.
先进行乘法运算,注意满60进1.
14.【答案】45°
【解析】解:∵∠BOC=∠AOB+∠AOC=90°+30°=120°,射线OM平分∠BOC,
∴∠COM= ∠BOC= ×120°=60°,
∵ON平分∠AOC,
∴∠CON= ∠AOC= ×30°=15°,
∴∠MON=∠COM﹣∠CON=60°﹣15°=45°.
故答案为:45°.
根据∠BOC=∠AOB+∠AOC算出∠BOC的度数,根据角平分线的定义由∠COM=?∠BOC,∠CON=?∠AOC,算出∠COM和∠CON的度数,再根据∠MON=∠COM﹣∠CON即可算出答案。
15.【答案】③;两点之间线段最短
【解析】解:结合图形可得应选择第③条路,所用的数学原理为两点之间线段最短.
故答案为:③,两点之间线段最短.
根据线段的性质,两点之间线段最短解答即可.
16.【答案】8
【解析】解:连接OA,OB,
∵正六边形,
∴∠AOB= =60°,
又OA=OB,
∴△AOB是等边三角形,
∴AB=OA=8.
故答案为:8.
求出正六边形的中心角,连接两个顶点,可得等边三角形,于是可得到正六边形的边长.
17.【答案】3
【解析】如图:∵AB=10cm,BC=4cm,∴AC=AB﹣BC=6cm,又点D是AC的中点,∴AD=AC=3cm,故答案为:3?
由AB=10cm,BC=4cm,可求出AC=AB﹣BC=6cm,再由点D是AC的中点,则可求得AD的长.
18.【答案】6或14
【解析】解:当点C在线段AB上时,AC=AB﹣BC=6cm,
当点C在线段AB的延长线上时,AC=AB+BC=14cm,
故答案为:6或14.
抓住已知直线AB上有一点C,因此分两种情况:当点C在线段AB上时,AC=AB﹣BC;当点C在线段AB的延长线上时,AC=AB+BC,计算即可得出答案。
19.【答案】①③
【解析】①∵ , 和 为角平分线,
∴ 与 为等腰三角形,
∴ , ,
∴ ,∴①正确;
②∵ 和 的平分线相交于点 ,
∴ ,
∴ ,
∴②错误;
③∵ 和 的平分线相交于点 ,
∴点 是 的内心,
点 到 各边的距离相等,③正确;
④连接 ,
∵点 是 的内心, , ,
∴ ,
∴④错误,
故答案为:①③.
根据平行线的性质及角平分线的性质得出得出∠BGE=∠EBG,根据等角对等边得出BE=EG,同理GF=FC,根据线段的和差及等量代换得出BE+CF=EG+GF=EF;根据角平分线的定义及角的和差得出∠GBC+∠GCB=(∠ABC+∠ACB),再根据三角形的内角和得出∠BGC=180°?(∠GBC+∠GCB)=180°?(180°?∠A)=90°+∠A ;根据三角形内心的定义得出点 G 是 △ABC 的内心,根据三角形内心的性质得出点 G 到 △ABC 各边的距离相等;连接 AG ,由S△AEF=AE?GD+AF?GD=(AE+AF)?GD=mn,综上所述即可得出答案。
20.【答案】;
【解析】解:连接AG,∵G(0,1)
∴OG=1,又AG=2
∴AO=
∵OC⊥AB
∴AB=2AO=
连接AC,过点G作GH⊥AC于点H,延长HG交AE 于点F,此时GF就是最短的,
∵C(0,3)
∴OC=3
根据勾股定理得AC=
∵CF⊥AE
∴HF=,
在Rt△CGH中,CG=OC-OG=3-1=2,CH=,
∴GH=
∴GF=HF-GH=
首先根据G点的坐标,得出OG的长,根据勾股定理算出AO的长,根据垂径定理即可得出AB的长;连接AC,过点G作GH⊥AC于点H,延长HG交AE 于点F,此时GF就是最短的,根据勾股定理得AC的长,根据直角三角形斜边上的中线等于斜边的一半得出HF的长,根据勾股定理算出GH的长,最后根据线段的和差即可算出答案。
三、作图题
21.【答案】解:如图,
【解析】根据直线没有端点,故可以向两个方向延伸,射线只有一个端点,可以向不是端点的方向延伸,线段有两个端点,故两个方向都不能延伸,从而画出图形。
22.【答案】解:如图,
.
【解析】此题主要考查了简单作图,解题的关键是熟练掌握直线、射线、线段的性质,根据直线、射线、线段的画法画图即可.
四、综合题
23.【答案】(1)解:∵∠AOM=90°,OC平分∠AOM???
∴∠AOC= ∠AOM=45°
∵∠AOC+∠AOD=180°
∴∠AOD=180°-∠AOC=180°-45°=135°
(2)解:∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°
∴∠CON=∠COB-∠BON=4x°-x°=3x°
∵OM平分∠CON????
∴∠COM=∠MON= ∠CON= x°
∵
解得:x=36
∴∠MON= x°= ×36°=54°
?即∠MON的度数为54°
【解析】(1)根据OC平分 ∠AOM求出∠AOC的度数,再根据邻补角的定义求出∠AOD的度数即可。
(2)设∠NOB=x°,利用∠BOC=4∠NOB,表示出∠BOC的度数,从而得出∠CON的度数,再根据角平分线的定义得出∠COM=∠MON,再根据∠NOB+∠MON=90°,建立方程求解,再求出∠MON的度数。
24.【答案】(1)解:∵CF平分∠DCE ,∠DCE=90°
∴
又∵∠3=45°
∴∠1=∠3
∴CF∥AB;
(2)解:∵∠D=30°? ∠1=45°
∴∠DFC=180°-∠D-∠1=105°
【解析】(1)根据角平分线的定义 :∠1=45°,根据三角板的各内角得出∠3=45°,从而得出∠1=∠3,根据内错角相等两直线平行得出结论;
(2)根据三角形的内角和得出∠DFC=180°-∠D-∠1=105°。
25.【答案】(1)解:图中小于平角的角∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB
(2)解:∵∠AOC=50°,OD平分∠AOC,
∴∠DOC= ∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
∴∠BOD=∠DOC+∠BOC=155°;
(3)解:∵∠DOE=90°,∠DOC=25°,
∴∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.
又∵∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,
∴∠COE=∠BOE,即OE平分∠BOC.
【解析】(1)结合图形写出小于平角的角即可得答案;
(2)由OD平分∠AOC可求出∠DOC的度数,由平角的定义可求出∠BOC的度数,再由∠BOD=∠DOC+∠BOC可求出答案;
(3)由∠COE=∠DOE﹣∠DOC可求出∠COE的度数,由∠BOE=∠BOD﹣∠DOE求出∠BOE的度数,进而可得答案.
26.【答案】(1)解:如图所画:
(2)解:如图所画:
(3)解:如图所画:
(4)解:如图所画:
【解析】根据直线、射线、线段的概念、两点之间,线段最短画图即可.
27.【答案】(1)解:①∵∠AON+∠BOM=90°,∠COM=∠MOB,∵∠AOC=30°,
∴∠BOC=2∠COM=150°,
∴∠COM=75°,
∴∠CON=15°,
∴∠AON=∠AOC﹣∠CON=30°﹣15°=15°,
解得:t=15°÷3°=5秒;
②是,理由如下:
∵∠CON=15°,∠AON=15°,
∴ON平分∠AOC
(2)解:5秒时OC平分∠MON,理由如下:∵∠AON+∠BOM=90°,∠CON=∠COM,
∵∠MON=90°,
∴∠CON=∠COM=45°,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∵∠AOC﹣∠AON=45°,
可得:6t﹣3t=15°,
解得:t=5秒
(3)解:OC平分∠MOB∵∠AON+∠BOM=90°,∠BOC=∠COM,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∴∠COM为 (90°﹣3t),
∵∠BOM+∠AON=90°,
可得:180°﹣(30°+6t)= (90°﹣3t),
解得:t= 秒;
如图:
【解析】(1)根据图形和题意得出∠AON+∠BOM=90°,∠CON+∠COM=90°,再根据∠AON=∠CON,即可得出OM平分∠BOC;(2)根据图形和题意得出∠AON+∠BOM=90°,∠CON=∠COM=45°,再根据转动速度从而得出答案;(3)分别根据转动速度关系和OC平分∠MOB画图即可.
(
第
6
页
共
17
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大七年级数学第四章《基本平面图形》单元检测试题及答案解析
一、单选题(共10题;共20分)
1.钟表在3点半时,它的时针与分针所成锐角是(????)
A.?70 ??????????????????????????????????????B.?85 ??????????????????????????????????????C.?75 ??????????????????????????????????????D.?90 ?
2.由上饶到南昌的某一次列车,运行途中停靠的车站依次是:上饶﹣横峰﹣弋阳﹣贵溪﹣鹰潭﹣余江﹣东乡﹣莲塘﹣南昌,那么要为这次列车制作的火车票有(?? )
A.?9种?????????????????????????????????????B.?18种?????????????????????????????????????C.?36种?????????????????????????????????????D.?72种
3.下列说法:①两条直线最多有一个公共点,②两条直线可能有无数个公共点,③两条线段可能有无数个公共点,④一条直线和一条线段可能有无数个公共点,其中正确的个数为( )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
4.下列说法正确的是(?? )
A.最小的有理数是0 B.射线OM的长度是5cm
C.两数相加,和一定大于任何一个加数 D.两点确定一条直线
5.已知∠AOB=50°,∠COB=30°,则∠AOC等于( )
A.?80°?????????????????????????????????B.?20°?????????????????????????????????C.?80°或20°?????????????????????????????????D.?无法确定
6.如图,AB∥CD,CE平分∠BCD,∠B=36°,则∠DCE等于( )
A.?18°???????????????????????????????????????B.?36°???????????????????????????????????????C.?45°???????????????????????????????????????D.?54°
7.下面表示∠ABC的图是(?? )
A.
B.
C.
D.
8.如图,量一量线段AB,BC,CA的长度,就能得到结论(?? )
A.?AB=BC+CA??????????????????B.?AB<BC+CA??????????????????C.?AB<|CA﹣BC|??????????????????D.?AB=|CA﹣BC|
9.如图,在直角△ABC中,∠C=90°,AD平分∠BAC,∠BAD=20°,则∠B的度数为(?? )
A.?40°???????????????????????????????????????B.?30°???????????????????????????????????????C.?60°???????????????????????????????????????D.?50°
10.下列语句,正确的是(? ).
A.?直线可表示一个平角;???????????????????????????????????B.?平角的两边向左右无限延伸;
C.?延长线段AB至点C,则∠ACB=180°;????????????D.?在一条直线上顺次取三点A、B、C,则∠ABC=180°
二、填空题(共10题;共24分)
11.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因________.
12.如图,正六边形ABCDEF的边长为2cm,点P为六边形内任一点.则点P到各边距离之和为________cm.
13.21°17′×5=________.
14.如图,一副直角三角板摆放在一起,射线OM平分∠BOC、ON平分∠AOC,∠MON的度数为________.
15.如图,已知从甲地到乙地共有四条路可走,你应选择第________?路,所用的数学原理为:________?
16.圆内接正六边形的边长是8cm,则该正六边形的半径为________
17.若C、D是线段AB上两点,D是线段AC的中点,AB=10cm,BC=4cm,则AD的长是________?cm.
18.已知线段AB=10cm,直线AB上有一点C,BC=4cm,则线段AC=________cm.
19.如图,在 中, 和 的平分线相交于点 ,过点 作 交 于 ,交 于 ,过点 作 于 ,下列四个结论:① ;② ;③点 到 各边的距离相等;④设 , , 则 .其中正确的结论是________.
20.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.
三、作图题(共2题;共10分)
21.如图,A、B、C三点不在同一条直线上,按要求画图:
( 1 )画直线AB;(2)画射线BC;(3)画线段CA.
22.已知四点A,B,C,D.根据下列语句,画出图形
①画直线AB;
②连接AC,BD,相交于点O;
③画射线AD,BC,交于点P.
四、综合题(共5题;共46分)
23.如图,直线AB与CD相交于点O, .
(1)如图1,若OC平分 ,求 的度数;
(2)如图2,若 ,且OM平分 ,求 的度数.
24.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
25.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
26.如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得CE=AB+BC;
(4)在线段BD上取点P,使PA+PC的值最小.
27.如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后,OM恰好平分∠BOC.①求t的值;②此时ON是否平分∠AOC?请说明理由;
(2)在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠MON?请说明理由;
(3)在(2)问的基础上,经过多长时间OC平分∠MOB?请画图并说明理由
答案解析部分
一、单选题
1.【答案】C
【解析】
∵3点半时,时针指向3和4中间,分针指向6.
钟表12个数字,每相邻两个数字之间的夹角为30°,半个格是15°,
∴3点半时,分针与时针的夹角正好是30°×2+15°=75度.
故选C.
2.【答案】C
【解析】解:每两站点都要设火车票,所以从一个城市出发到其他8个城市有8种车票,
但是已知中是由上饶到南昌的某一次列车,运行途中停靠的车站依次是:上饶﹣横峰﹣弋阳﹣贵溪﹣鹰潭﹣余江﹣东乡﹣莲塘﹣南昌,故没有往返车票,是单程车票,
所以要为这次列车制作的火车票有 ×8×9=36(种).
故选:C.
每两站点都要设火车票,从一个城市出发到其他8个城市有8种车票,进而得出答案.
3.【答案】C
【解析】解:①两条直线最多有一个公共点,错误;
②两条直线可能有无数个公共点,正确;
③两条线段可能有无数个公共点,正确;
④一条直线和一条线段可能有无数个公共点,正确.
故选C
根据直线、线段的相交的交点个数进行判断即可.
4.【答案】D
【解析】解:A、没有最小的有理数,故A不符合题意;
B、射线没有长度,故B不符合题意;
C、两个负数相加和小于任何一个加数,故C不符合题意;
D、两点确定一条直线,故D符合题意;
故选:D.
根据有理数的意义,有理数的加法,直线的性质,射线的定义,可得答案.
5.【答案】C
【解析】解:①如图1,OC在∠AOB内,
∵∠AOB=50°,∠COB=30°,
∴∠AOC=∠AOB﹣∠COB=50°﹣30°=20°;
②如图2,OC在∠AOB外,
∵∠AOB=50°,∠COB=30°,
∴∠AOC=∠AOB+∠COB=50°+30°=80°;
综上所述,∠AOC的度数是20°或80°.
故选:C.
解答此题的关键是明确此题射线OC的位置,有2种可能,然后根据图形和∠AOB=50°,即可求出∠AOC的度数.
6.【答案】A
【解析】解:∵AB∥CD,
∴∠BCD=∠B=36°,
∵CE平分∠BCD,
∴∠DC=18°
故选:A.
根据两直线平行,内错角相等可得∠BCD=∠B,再根据角平分线的定义求出∠DCE,从而求解.本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.
7.【答案】C
【解析】解:A、有四个小于平角的角,没有∠ABC,故错误;
B、用三个大写字母表示角,表示角顶点的字母在中间,应为∠BCA,故错误;
C、用三个大写字母表示角,表示角顶点的字母在中间,应为∠ABC,故正确;
D、用三个大写字母表示角,表示角顶点的字母在中间,应为∠BAC,故错误.
故选:C.
根据角的概念,对选项进行一一分析,排除错误答案.
8.【答案】B
【解析】解:根据两边之和大于第三边可得:BC+CA>AB, 故可得B正确.
故选B.
根据三角形的三边关系:两边之和大于第三边即可得出答案.
9.【答案】D
【解析】分析】利用角平分线的性质计算.
∵AD的平分∠BAC,∠BAD=20°
∴∠CAB=40°
又∵∠C=90°
∴∠B=50°
故选D.
【点评】此题综合考查角平分线,直角三角形的两锐角互余.
10.【答案】D
【解析】A. 一个角由有公共端点的两射线组成,一个平角的两边在一条直线上,则一条直线不是一个平角,所以错误;B.角的两边是射线,射线是无限长的,不能说无限延伸射线,故说法错误;? C.角的两边应该是射线,延长线段AB至点C,AB和BC都是线段,故错误;?? D . 在一条直线上顺次取三点A、B、C,则∠ABC是平角,等于180°,正确;故答案选D.
根据角的定义意义进行分析,然后排出错误的答案.
二、填空题
11.【答案】两点之间线段最短
【解析】解:为抄近路践踏草坪原因是:两点之间线段最短.
故答案为:两点之间线段最短.
为抄近路践踏草坪原因是:两点之间线段最短.
12.【答案】18
【解析】解:过P作AB的垂线,交AB、DE分别为H、K,连接BD,
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,且P到AF与CD的距离和及P到EF、BC的距离和均为HK的长,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,
∴BD∥HK,且BD=HK,
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=2×2×=6,
∴点P到各边距离之和为3BD=3×6=18.
故答案为:18.
过P作AB的垂线,交AB、DE分别为H、K,连接BD,由正六边形的性质可知AB∥DE,AF∥CD,BC∥EF,故HK⊥DE,过C作CG⊥BD,由等腰三角形的性质及正六边形的内角和定理可知,DB⊥AB⊥DE,再由锐角三角函数的定义可求出BG的长,进而可求出BD的长,由正六边形的性质可知点P到AF与CD的距离和及P到EF、BC的距离和均为BD的长,故可得出结论.
13.【答案】106°25′
【解析】解:21°17′×5=105°85′=106°25′.
故答案为:106°25′.
先进行乘法运算,注意满60进1.
14.【答案】45°
【解析】解:∵∠BOC=∠AOB+∠AOC=90°+30°=120°,射线OM平分∠BOC,
∴∠COM= ∠BOC= ×120°=60°,
∵ON平分∠AOC,
∴∠CON= ∠AOC= ×30°=15°,
∴∠MON=∠COM﹣∠CON=60°﹣15°=45°.
故答案为:45°.
根据∠BOC=∠AOB+∠AOC算出∠BOC的度数,根据角平分线的定义由∠COM=?∠BOC,∠CON=?∠AOC,算出∠COM和∠CON的度数,再根据∠MON=∠COM﹣∠CON即可算出答案。
15.【答案】③;两点之间线段最短
【解析】解:结合图形可得应选择第③条路,所用的数学原理为两点之间线段最短.
故答案为:③,两点之间线段最短.
根据线段的性质,两点之间线段最短解答即可.
16.【答案】8
【解析】解:连接OA,OB,
∵正六边形,
∴∠AOB= =60°,
又OA=OB,
∴△AOB是等边三角形,
∴AB=OA=8.
故答案为:8.
求出正六边形的中心角,连接两个顶点,可得等边三角形,于是可得到正六边形的边长.
17.【答案】3
【解析】如图:∵AB=10cm,BC=4cm,∴AC=AB﹣BC=6cm,又点D是AC的中点,∴AD=AC=3cm,故答案为:3?
由AB=10cm,BC=4cm,可求出AC=AB﹣BC=6cm,再由点D是AC的中点,则可求得AD的长.
18.【答案】6或14
【解析】解:当点C在线段AB上时,AC=AB﹣BC=6cm,
当点C在线段AB的延长线上时,AC=AB+BC=14cm,
故答案为:6或14.
抓住已知直线AB上有一点C,因此分两种情况:当点C在线段AB上时,AC=AB﹣BC;当点C在线段AB的延长线上时,AC=AB+BC,计算即可得出答案。
19.【答案】①③
【解析】①∵ , 和 为角平分线,
∴ 与 为等腰三角形,
∴ , ,
∴ ,∴①正确;
②∵ 和 的平分线相交于点 ,
∴ ,
∴ ,
∴②错误;
③∵ 和 的平分线相交于点 ,
∴点 是 的内心,
点 到 各边的距离相等,③正确;
④连接 ,
∵点 是 的内心, , ,
∴ ,
∴④错误,
故答案为:①③.
根据平行线的性质及角平分线的性质得出得出∠BGE=∠EBG,根据等角对等边得出BE=EG,同理GF=FC,根据线段的和差及等量代换得出BE+CF=EG+GF=EF;根据角平分线的定义及角的和差得出∠GBC+∠GCB=(∠ABC+∠ACB),再根据三角形的内角和得出∠BGC=180°?(∠GBC+∠GCB)=180°?(180°?∠A)=90°+∠A ;根据三角形内心的定义得出点 G 是 △ABC 的内心,根据三角形内心的性质得出点 G 到 △ABC 各边的距离相等;连接 AG ,由S△AEF=AE?GD+AF?GD=(AE+AF)?GD=mn,综上所述即可得出答案。
20.【答案】;
【解析】解:连接AG,∵G(0,1)
∴OG=1,又AG=2
∴AO=
∵OC⊥AB
∴AB=2AO=
连接AC,过点G作GH⊥AC于点H,延长HG交AE 于点F,此时GF就是最短的,
∵C(0,3)
∴OC=3
根据勾股定理得AC=
∵CF⊥AE
∴HF=,
在Rt△CGH中,CG=OC-OG=3-1=2,CH=,
∴GH=
∴GF=HF-GH=
首先根据G点的坐标,得出OG的长,根据勾股定理算出AO的长,根据垂径定理即可得出AB的长;连接AC,过点G作GH⊥AC于点H,延长HG交AE 于点F,此时GF就是最短的,根据勾股定理得AC的长,根据直角三角形斜边上的中线等于斜边的一半得出HF的长,根据勾股定理算出GH的长,最后根据线段的和差即可算出答案。
三、作图题
21.【答案】解:如图,
【解析】根据直线没有端点,故可以向两个方向延伸,射线只有一个端点,可以向不是端点的方向延伸,线段有两个端点,故两个方向都不能延伸,从而画出图形。
22.【答案】解:如图,
.
【解析】此题主要考查了简单作图,解题的关键是熟练掌握直线、射线、线段的性质,根据直线、射线、线段的画法画图即可.
四、综合题
23.【答案】(1)解:∵∠AOM=90°,OC平分∠AOM???
∴∠AOC= ∠AOM=45°
∵∠AOC+∠AOD=180°
∴∠AOD=180°-∠AOC=180°-45°=135°
(2)解:∵∠BOC=4∠NOB
∴设∠NOB=x°,∠BOC=4x°
∴∠CON=∠COB-∠BON=4x°-x°=3x°
∵OM平分∠CON????
∴∠COM=∠MON= ∠CON= x°
∵
解得:x=36
∴∠MON= x°= ×36°=54°
?即∠MON的度数为54°
【解析】(1)根据OC平分 ∠AOM求出∠AOC的度数,再根据邻补角的定义求出∠AOD的度数即可。
(2)设∠NOB=x°,利用∠BOC=4∠NOB,表示出∠BOC的度数,从而得出∠CON的度数,再根据角平分线的定义得出∠COM=∠MON,再根据∠NOB+∠MON=90°,建立方程求解,再求出∠MON的度数。
24.【答案】(1)解:∵CF平分∠DCE ,∠DCE=90°
∴
又∵∠3=45°
∴∠1=∠3
∴CF∥AB;
(2)解:∵∠D=30°? ∠1=45°
∴∠DFC=180°-∠D-∠1=105°
【解析】(1)根据角平分线的定义 :∠1=45°,根据三角板的各内角得出∠3=45°,从而得出∠1=∠3,根据内错角相等两直线平行得出结论;
(2)根据三角形的内角和得出∠DFC=180°-∠D-∠1=105°。
25.【答案】(1)解:图中小于平角的角∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB
(2)解:∵∠AOC=50°,OD平分∠AOC,
∴∠DOC= ∠AOC=25°,∠BOC=180°﹣∠AOC=130°,
∴∠BOD=∠DOC+∠BOC=155°;
(3)解:∵∠DOE=90°,∠DOC=25°,
∴∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.
又∵∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,
∴∠COE=∠BOE,即OE平分∠BOC.
【解析】(1)结合图形写出小于平角的角即可得答案;
(2)由OD平分∠AOC可求出∠DOC的度数,由平角的定义可求出∠BOC的度数,再由∠BOD=∠DOC+∠BOC可求出答案;
(3)由∠COE=∠DOE﹣∠DOC可求出∠COE的度数,由∠BOE=∠BOD﹣∠DOE求出∠BOE的度数,进而可得答案.
26.【答案】(1)解:如图所画:
(2)解:如图所画:
(3)解:如图所画:
(4)解:如图所画:
【解析】根据直线、射线、线段的概念、两点之间,线段最短画图即可.
27.【答案】(1)解:①∵∠AON+∠BOM=90°,∠COM=∠MOB,∵∠AOC=30°,
∴∠BOC=2∠COM=150°,
∴∠COM=75°,
∴∠CON=15°,
∴∠AON=∠AOC﹣∠CON=30°﹣15°=15°,
解得:t=15°÷3°=5秒;
②是,理由如下:
∵∠CON=15°,∠AON=15°,
∴ON平分∠AOC
(2)解:5秒时OC平分∠MON,理由如下:∵∠AON+∠BOM=90°,∠CON=∠COM,
∵∠MON=90°,
∴∠CON=∠COM=45°,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∵∠AOC﹣∠AON=45°,
可得:6t﹣3t=15°,
解得:t=5秒
(3)解:OC平分∠MOB∵∠AON+∠BOM=90°,∠BOC=∠COM,
∵三角板绕点O以每秒3°的速度,射线OC也绕O点以每秒6°的速度旋转,
设∠AON为3t,∠AOC为30°+6t,
∴∠COM为 (90°﹣3t),
∵∠BOM+∠AON=90°,
可得:180°﹣(30°+6t)= (90°﹣3t),
解得:t= 秒;
如图:
【解析】(1)根据图形和题意得出∠AON+∠BOM=90°,∠CON+∠COM=90°,再根据∠AON=∠CON,即可得出OM平分∠BOC;(2)根据图形和题意得出∠AON+∠BOM=90°,∠CON=∠COM=45°,再根据转动速度从而得出答案;(3)分别根据转动速度关系和OC平分∠MOB画图即可.
(
第
6
页
共
17
页
)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
