2018年秋季学期期末复习专用:北师大版七年级数学第六章《数据的收集与整理》单元检测试题及答案解析
文档属性
| 名称 | 2018年秋季学期期末复习专用:北师大版七年级数学第六章《数据的收集与整理》单元检测试题及答案解析 |  | |
| 格式 | zip | ||
| 文件大小 | 333.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-24 09:03:04 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大七年级数学第六章《数据的收集与整理》单元检测试题及答案解析
一、单选题(共10题;共20分)
1.下列说法,错误的是(?? )
A.?为了解一种灯泡的使用寿命,宜采用普查的方法
B.?众数在一组数据中若存在,可以不唯一
C.?方差反映了一组数据与其平均数的偏离程度
D.?对于简单随机样本,可以用样本的方差去估计总体的方差
2.下面的折线图描述了某地某日的气温变化情况.根据图中信息,下列说法错误的是( )
A.?4:00气温最低???????????????????????????????????????????????????B.?6:00气温为24℃
C.?14:00气温最高?????????????????????????????????????????????????D.?气温是30℃的时刻为16:00
3.(2013?盘锦)下列调查中适合采用全面调查的是( )
A.?调查市场上某种白酒的塑化剂的含量???????????????????????B.?调查鞋厂生产的鞋底能承受弯折次数
C.?了解某火车的一节车厢内感染禽流感病毒的人数?????D.?了解某城市居民收看辽宁卫视的时间
4.如图是甲乙两个学校男女人数统计图,女生人数多的学校是( )
A.?甲校??????????????????????????B.?乙校?????????????????????????C.?两个学校人数一样多???????????????????????????D.?无法确定
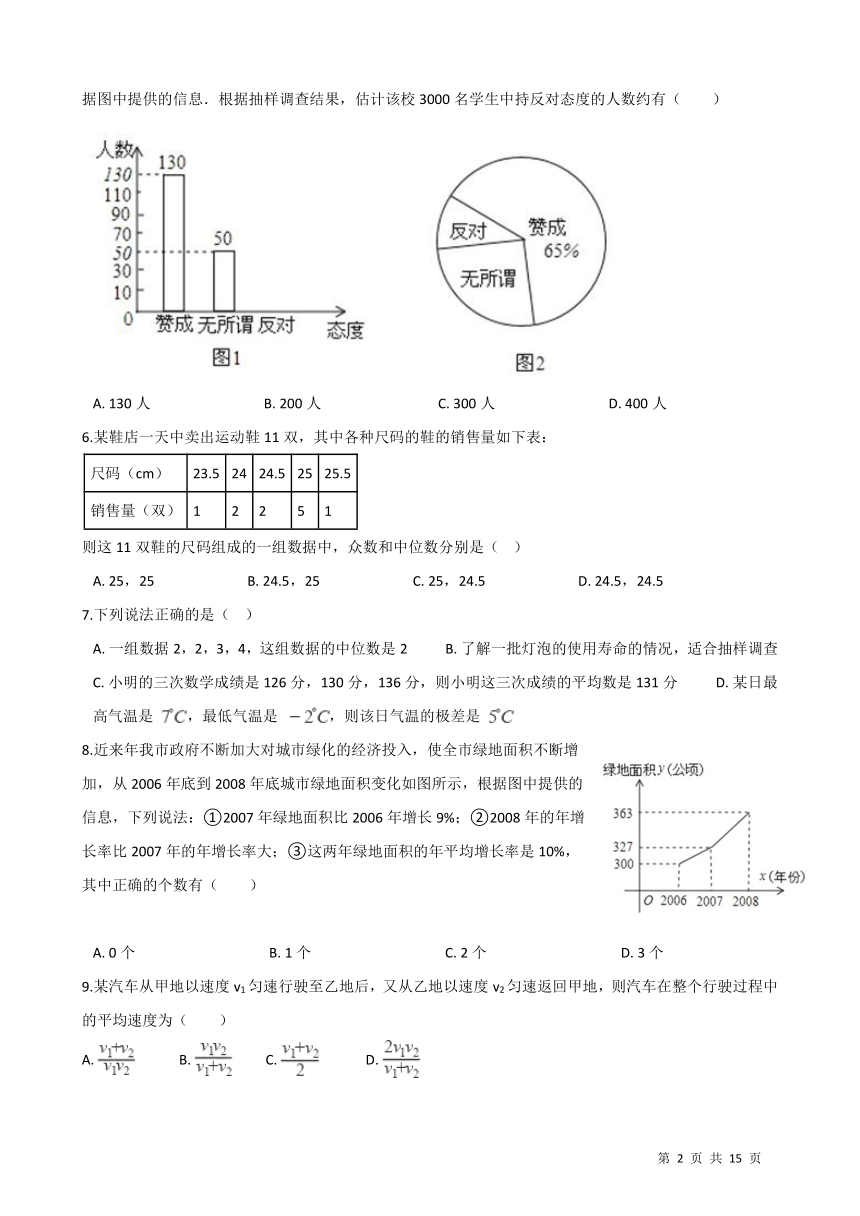
5.以“光盘”为主题的公益活动越来越受到社会的关注,某校为培养学生勤俭节约的习惯,随机抽查了部分学生(态度分为:赞成、无所谓、反对),并将抽查结果绘制成图1和图2两个统计图(不完整),请根据图中提供的信息.根据抽样调查结果,估计该校3000名学生中持反对态度的人数约有( )
A.?130人?????????????????????????????????B.?200人??????????????????????????????????C.?300人?????????????????????????????????D.?400人
6.某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:
尺码(cm) 23.5 24 24.5 25 25.5
销售量(双) 1 2 2 5 1
则这11双鞋的尺码组成的一组数据中,众数和中位数分别是(????)
A.?25,25???????????????????????????B.?24.5,25???????????????????????????C.?25,24.5???????????????????????????D.?24.5,24.5
7.下列说法正确的是(?? )
A.?一组数据2,2,3,4,这组数据的中位数是2???????????B.?了解一批灯泡的使用寿命的情况,适合抽样调查
C.?小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分???????????D.?某日最高气温是 ,最低气温是 ,则该日气温的极差是
8.近来年我市政府不断加大对城市绿化的经济投入,使全市绿地面积不断增加,从2006年底到2008年底城市绿地面积变化如图所示,根据图中提供的信息,下列说法:①2007年绿地面积比2006年增长9%;②2008年的年增长率比2007年的年增长率大;③这两年绿地面积的年平均增长率是10%,其中正确的个数有( )
?
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
9.某汽车从甲地以速度v1匀速行驶至乙地后,又从乙地以速度v2匀速返回甲地,则汽车在整个行驶过程中的平均速度为( )
A.?????????????B.??????????C.??????????????D.?
10.如图是甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是(???)
A.?甲户比乙户多?????????????B.?乙户比甲户多?????????????C.?甲、乙两户一样多?????????????D.?无法确定哪一户多
二、填空题(共10题;共13分)
11.分析下列四种调查:①了解我们学校所有八年级学生的视力状况;②估计小明家一年总用电量;③登飞机前,对所有旅客进行安全检查;④了解中小学生的主要娱乐方式;其中应作普查的是:________(填序号)
12.某县有80万人口,其中各民族所占比例如上图所示,则该县少数民族
人口共有________万人.
13.空气是由多种气体混合而成的,教师为了简明扼要的向学生介绍空气的
组成情况,使用________?统计图描述数据较好.
14.某校九年级准备开展春季研学活动,对全年级学生各自最想去的活动地点进行了调查,把调查结果制成了如下扇形统计图,则“世界之窗”对应扇形的圆心角为________度.
15.将容量为n的样本中的数据分成6组,绘制频率分布直方图.若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于________?.
16.(2015?绥化)在2015年的体育考试中某校6名学生的体育成绩统计如图所示,这组数据的中位数是?________.
?
17.(2011?防城港)如图,是某校三个年级学生人数分布扇形统计图,则九年级学生人数所占扇形的圆心角的度数为________.
18.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有________人.
19.新华高科技股份有限公司董事会决定今年用13亿资金投资发展项目,现有6个项目可供选择(每个项目或者被全部投资,或者不被投资),各项目所需投资金额和预计年均收益如下表:
?项目 ?A ?B C D ?E ?F
投资(亿元) ?5 ?2 ?6 ?4 ?6 ?8
?收益(亿元) ?0.55 ?0.4 0.6 ?0.4 ?0.9 ?1
如果要求所有投资的项目的收益总额不得低于1.6亿元,那么,当选择的投资项目是________?时,投资的收益总额最大.
20.为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(Ⅰ)被抽样调查的学生有 ________?人,并补全条形统计图________?;
(Ⅱ)每天户外活动时间的中位数是?________? (小时);
(Ⅲ)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有________?人?
三、综合题(共5题;共69分)
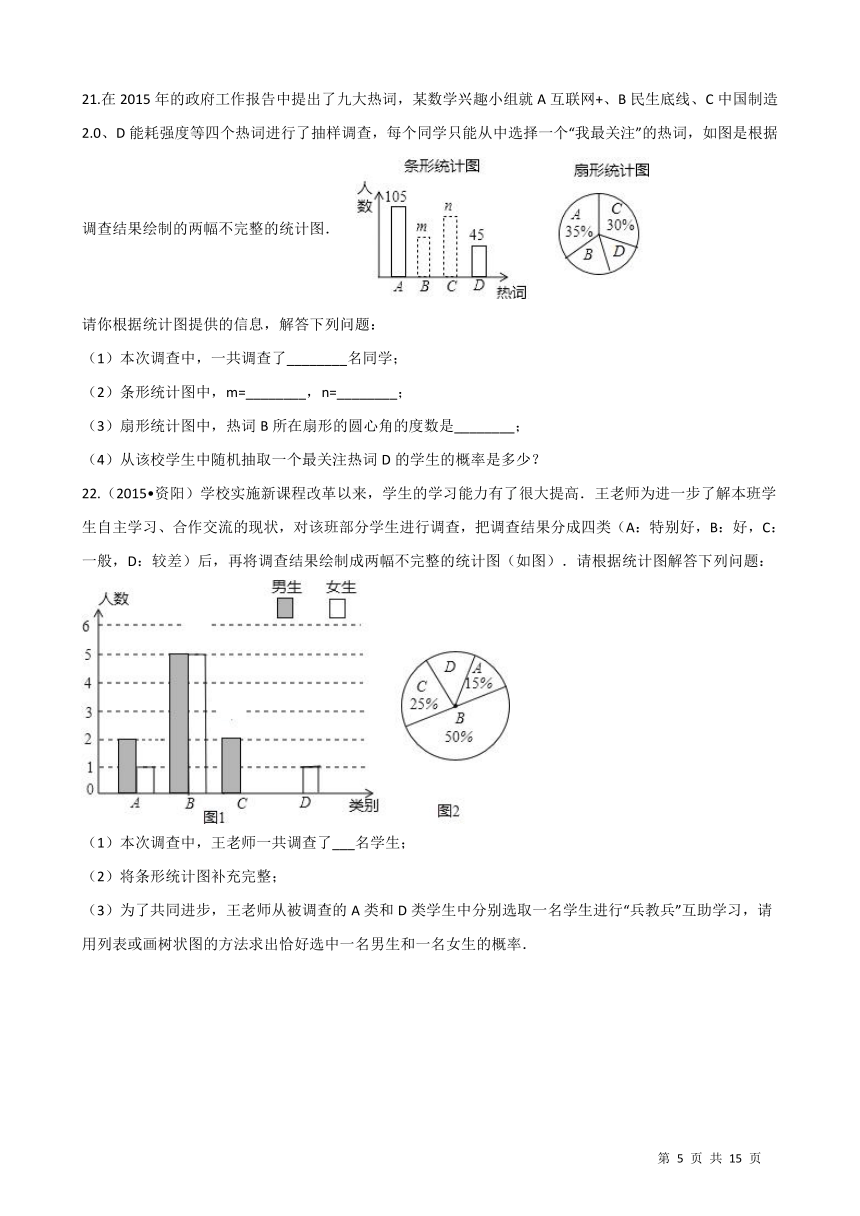
21.在2015年的政府工作报告中提出了九大热词,某数学兴趣小组就A互联网+、B民生底线、C中国制造2.0、D能耗强度等四个热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了________名同学;
(2)条形统计图中,m=________,n=________;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是________;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
22.(2015?资阳)学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了___名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
23.“知识改变命运,科技繁荣祖国”,某区中小学每年都要举办一届科技比赛,如图为某区某校2017年参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图.
(1)该校参加机器人、建模比赛的人数分别是________人和________人;
(2)该校参加科技比赛的总人数是________人,电子百拼所在扇形的圆心角的度数是________°,并把条形统计图补充完整;
(3)从全区中小学参加科技比赛选手中随机抽取85人,其中有34人获奖.2017年某区中小学参加科技比赛人数共有3625人,请你估算2017年参加科技比赛的获奖人数约是多少人?
24.为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2.
(1)该班共有多少名学生?
(2)请在图1中将“乒乓球”部分的图形补充完整;
(3)若全年级共有1200名学生,估计全年级参加乒乓球活动的学生有多少名?
(4)求出扇形统计图中表示“足球”的扇形的圆心角度数.
25.“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.
答案解析部分
一、单选题
1.【答案】A
【解析】A一种灯泡有很多,数量很庞大,了解它的使用寿命时宜采用抽样的方法,所以A错误;
B众数在一组数据中若存在,可以有一个,也可有有两个、三个,所以B正确;
根据方差的意义,方差反映的是一组数据的波动大小,所以C正确;
D对于简单随机样本,总体数目不大,我们可以用样本的方差去估计总体的方差,所以D正确。
2.【答案】D
【解析】解:A、由横坐标看出4:00气温最低是24℃,故A正确;
B、由纵坐标看出6:00气温为24℃,故B正确;
C、由横坐标看出14:00气温最高31℃;
D、由横坐标看出气温是30℃的时刻是12:00,16:00,故D错误;
故选:D.
根据观察函数图象的横坐标,可得时间,根据观察函数图象的纵坐标,可得气温.
3.【答案】C
【解析】解:A、数量较大,具有破坏性,适合抽查;
B、数量较大,具有破坏性,适合抽查;
C、事关重大,因而必须进行全面调查;
D、数量较大,不容易普查,适合抽查.
故选C.
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
4.【答案】D
【解析】解:∵两校的人数不能确定,
∴通过扇形统计图无法比较女生人数的多少.
故选D.
根据扇形统计图的特点进行解答即可.
5.【答案】C
【解析】解:130÷65%=200(名),
200﹣130﹣50=20(名),
3000×=300(名),
答:该校3000名学生中持反对态度的人数约有300人,
故选:C.
根据赞成是130人,占65%即可求得总人数,利用总人数减去另外两项的人数,求得反对的人数,利用3000乘以持反对态度的比例即可.
6.【答案】A
【解析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
从小到大排列此数据为:23.5、24、24、24.5、24.5、25、25、25、25、25、26,
数据25出现了五次最多为众数.
25处在第6位为中位数.所以中位数是25,众数是25.
故选A.
7.【答案】B
【解析】解:A、一组数据2,2,3,4,这组数据的中位数是2.5,不符合题意;
B、了解一批灯泡的使用寿命的情况,适合抽样调查,符合题意;
C、小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是130 分,不符合题意;
D、某日最高气温是7℃,最低气温是-2℃,则改日气温的极差是7-(-2)=9℃,不符合题意;
故答案为:B.
根据中位数的定义,一组数据从小到大排列后,处于最中间位置的数就是中位数,如果这组数据的个数是偶数个,则处于中间位置的两个数的平均数就是该组数据的中位数;抽样调查适合于要求的数据不是那么精准,具有破坏性,等的调查;根据平均数的计算方法,把该组数据的总和除以该组数据的个数即可得出该组数据的平均数;求一天温差就是用当天的最高温度减去最低温度,根据有理数的减法法则即可得出答案。
8.【答案】D
【解析】解:①2007年绿地面积比2006年增长=9%,正确;
②2008年的年增长率是≈11%>9%,所以比2007年的年增长率大,正确;
③这两年绿地面积的年平均增长率是=10%,正确.
故选D.
解决本题需要从统计图获取信息,由此关键是明确图表中数据的来源及所表示的意义,依据所示的实际意义获取正确的信息.
9.【答案】D
【解析】解:设两地距离为S,从甲地行驶至乙地的时间为T1 , 从乙地返回甲地的时间为T2 ,
则有T1=, T2=;
∴平均速度===;
故本题选D.
由题意知,设两地距离为S,从甲地行驶至乙地的时间为T1 , 从乙地返回甲地的时间为T2 , 则关键时间的计算公式求得T1及T2 , 再关键平均速度的计算公式即可求得平均速度.
10.【答案】D
【解析】根据扇形统计图的特征分析即可.
不知道甲、乙两户居民家庭全年支出的总费用,只知道百分比,无法确定哪一户多,故选D.
二、填空题
11.【答案】③
【解析】根据普查的特征,易得③,其余选用抽样调查合适.
普查适合于工作量比较小,不具有破坏性,对调查结果要求比较精确等的调查,根据普查的意义即可一一判断。
12.【答案】12
【解析】80×(8%+4%+3%)
=80×15%
=12(万人)
故答案为:12
把总人数看作单位“1”,用总人数乘少数民族所占的分率和即可求出少数民族的人口数.
13.【答案】扇形
【解析】解:根据题意,得
要直观的、简明扼要的向学生介绍空气的组成情况,即所占的比例,应选用扇形统计图.
扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
14.【答案】90
【解析】解:“世界之窗”对应扇形的圆心角=360°×(1-10%-30%-20%-15%)=90°,
故答案为:90.
“世界之窗”对应扇形的圆心角的度数=360°世界之窗”所占的百分比,计算即可。
15.【答案】60
【解析】解:设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x,x,?则2x+3x+4x+6x+4x+x=1,
?解得 ,
?所以前三组数据的频率分别是 ,
?故前三组数据的频数之和等于 =27,
?解得n=60.故答案为60.
根据题意得到第一组至第六组数据的频率之和是1,得到前三组数据的频率分别是2÷20,3÷20,4÷20;由前三组数据的频数之和等于27,求出样本容量n的值.
16.【答案】26
【解析】解:把这组数据从小到大排列,最中间两个数的平均数是(26+26)÷2=26,则中位数是26.
故答案为:26.
根据中位数的定义,即可解答.
17.【答案】144°
【解析】解:由图可知九年级学生人数所占扇形统计图的百分比为:1﹣35%﹣25%=40%,
∴九年级学生人数所占扇形的圆心角的度数为360×40%=144°,
故答案为144°.
先根据图求出九年级学生人数所占扇形统计图的百分比为40%,又知整个扇形统计图的圆心角为360度,再由360乘以40%即可得到答案.
18.【答案】10
【解析】解:全班的人数是:20÷40%=50(人), AB型的所占的百分比是: =10%,
则O型血的人数是:50(1﹣40%﹣30%﹣10%)=10(人).
故答案为:10.
根据A型血的有20人,所占的百分比是40%即可求得班级总人数,根据AB型所对应的扇形圆心角的度数求得对应的百分比,则用总人数乘以O型血所对应的百分比即可求解.
19.【答案】A、B、E
【解析】解:A:=0.11,B:=0.2,C:, D:=0.1,E:=0.15,F:=0.125
收益从大到小依次是:B>F>E>A>C=D
又∵总投资不能超过13亿,收益总额不低于1.6亿,
∴只有A,B,E比较符合要求
故选:A,B,E
分别求出收益与投资的比例,结合总投资不能超过13亿,收益总额不低于1.6亿,可求出.
20.【答案】500;;1;800
【解析】解:(Ⅰ)∵0.5小时的有100人占被调查总人数的20%,
∴被调查的人数有:100÷20%=500,
1.5小时的人数有:500﹣100﹣200﹣80=120,
补全的条形统计图如下图所示,
故答案为:500;(Ⅱ)由(1)可知被调查学生500人,由条形统计图可得,中位数是1小时,
故答案为:1;(Ⅲ)由题意可得,
该校每天户外活动时间超过1小时的学生数为: ×2000=800人,
即该校每天户外活动时间超过1小时的学生有800人.
(Ⅰ)根据条形统计图和扇形统计图可以求得被调查学生总数和1.5小时的学生数,从而可以将条形统计图补充完整;(Ⅱ)根据条形统计图可以得到这组数据的中位数;(Ⅲ)根据条形统计图可以求得校共有2000名学生,该校每天户外活动时间超过1小时的学生有多少人.
三、综合题
21.【答案】(1)300
(2)60;90
(3)72°
(4)解: . 答:从该校学生中随机抽取一个最关注热词D的学生的概率是
【解析】解:(1.)105÷35%=300(人). 故答案为:300;
(2.)n=300×30%=90(人),m=300﹣105﹣90﹣45=60(人).
故答案为:60,90;
(3.) ×360°=72°.
故答案为:72°;
(1)根据A的人数为105人,所占的百分比为35%,求出总人数,即可解答;(2)C所对应的人数为:总人数×30%,B所对应的人数为:总人数﹣A所对应的人数﹣C所对应的人数﹣D所对应的人数,即可解答;(3)根据B所占的百分比×360°,即可解答;(4)根据概率公式,即可解答.
22.【答案】(1)解:根据题意得:王老师一共调查学生:(2+1)÷15%=20(名);
故答案为:20;
(2)解:∵C类女生:20×25%﹣2=3(名);D类男生:20×(1﹣15%﹣50%﹣25%)﹣1=1(名);
如图:
(3)解:列表如下:A类中的两名男生分别记为A1和A2,
男A1 男A2 …(7分)
女A
男D 男A1男D 男A2男D 女A男D
女D 男A1女D 男A2女D 女A女D
共有6种等可能的结果,其中,一男一女的有3种,所以所选两位同学恰好是一位男生和一位女生的概率为:=.
【解析】(1)由题意可得:王老师一共调查学生:(2+1)÷15%=20(名);
(2)由题意可得:C类女生:20×25%﹣2=3(名);D类男生:20×(1﹣15%﹣50%﹣25%)﹣1=1(名);继而可补全条形统计图;
(3)首先根据题意列出表格,再利用表格求得所有等可能的结果与恰好选中一名男生和一名女生的情况,继而求得答案.
23.【答案】(1)4.;6.
(2)24.;120.
(3)解:34÷85=0.4,
0.4×3625=1450(人).
答:今年参加科技比赛比赛的获奖人数约是1450人.
【解析】解:(1)由条形统计图可得:该校参加机器人、建模比赛的人数分别是4人,6人,
故答案为:4人,6人.
(2)该校参加科技比赛的总人数是:6÷25%=24,
电子百拼所在扇形的圆心角的度数是:(24﹣6﹣6﹣4)÷24×360°=120°,
故答案为:24,120°.
条形统计图补充如下:
(1)由条形统计图即可得该校参加机器人、建模比赛的人数.
(2)由条形统计图和扇形统计图可得建模的人数和百分比,再根据总数=频数÷频率即可得出该校参加科技比赛的总人数.
(3)根据频率=频数÷总数,再用频数=总数×频率即可得出今年参加科技比赛比赛的获奖人数.
24.【答案】(1)解:20÷0.4=50(名)
(2)解:乒乓球”部分的人数是:50-15-10-20=5
(3)解:参加乒乓球活动的学生是:1200× =120(名)
(4)解:360°× =72°
【解析】(1)根据统计图中篮球的人数和百分比求出该班共有的学生数;(2)由(1)中的总人数求出“乒乓球”的人数,补全统计图;(3)由(1)(2)求出乒乓球的百分比,求出全年级参加乒乓球活动的学生的人数;(4)根据足球的百分比求出“足球”的扇形的圆心角度数.
25.【答案】(1)解:家长总数:200÷50%=400名, 表示“无所谓”人数:400﹣200﹣16﹣400×26%=80名,补全图①,
(2)解:80÷400×360°=72°
(3)解:16÷400=
【解析】(1)由图象可以得出基本赞成的有200人占50%,可以求出总数,由总数可以求出非常赞成的人数和无所谓的人数.(2)由(1)的总数求出无所谓的百分比再乘以360°就可以求出圆心角的度数.(3)这次受调查的家长不赞成的人数除以总数就是抽到恰好是“不赞成”态度的家长的概率.
(
第
1
页
共
16
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
北师大七年级数学第六章《数据的收集与整理》单元检测试题及答案解析
一、单选题(共10题;共20分)
1.下列说法,错误的是(?? )
A.?为了解一种灯泡的使用寿命,宜采用普查的方法
B.?众数在一组数据中若存在,可以不唯一
C.?方差反映了一组数据与其平均数的偏离程度
D.?对于简单随机样本,可以用样本的方差去估计总体的方差
2.下面的折线图描述了某地某日的气温变化情况.根据图中信息,下列说法错误的是( )
A.?4:00气温最低???????????????????????????????????????????????????B.?6:00气温为24℃
C.?14:00气温最高?????????????????????????????????????????????????D.?气温是30℃的时刻为16:00
3.(2013?盘锦)下列调查中适合采用全面调查的是( )
A.?调查市场上某种白酒的塑化剂的含量???????????????????????B.?调查鞋厂生产的鞋底能承受弯折次数
C.?了解某火车的一节车厢内感染禽流感病毒的人数?????D.?了解某城市居民收看辽宁卫视的时间
4.如图是甲乙两个学校男女人数统计图,女生人数多的学校是( )
A.?甲校??????????????????????????B.?乙校?????????????????????????C.?两个学校人数一样多???????????????????????????D.?无法确定
5.以“光盘”为主题的公益活动越来越受到社会的关注,某校为培养学生勤俭节约的习惯,随机抽查了部分学生(态度分为:赞成、无所谓、反对),并将抽查结果绘制成图1和图2两个统计图(不完整),请根据图中提供的信息.根据抽样调查结果,估计该校3000名学生中持反对态度的人数约有( )
A.?130人?????????????????????????????????B.?200人??????????????????????????????????C.?300人?????????????????????????????????D.?400人
6.某鞋店一天中卖出运动鞋11双,其中各种尺码的鞋的销售量如下表:
尺码(cm) 23.5 24 24.5 25 25.5
销售量(双) 1 2 2 5 1
则这11双鞋的尺码组成的一组数据中,众数和中位数分别是(????)
A.?25,25???????????????????????????B.?24.5,25???????????????????????????C.?25,24.5???????????????????????????D.?24.5,24.5
7.下列说法正确的是(?? )
A.?一组数据2,2,3,4,这组数据的中位数是2???????????B.?了解一批灯泡的使用寿命的情况,适合抽样调查
C.?小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是131分???????????D.?某日最高气温是 ,最低气温是 ,则该日气温的极差是
8.近来年我市政府不断加大对城市绿化的经济投入,使全市绿地面积不断增加,从2006年底到2008年底城市绿地面积变化如图所示,根据图中提供的信息,下列说法:①2007年绿地面积比2006年增长9%;②2008年的年增长率比2007年的年增长率大;③这两年绿地面积的年平均增长率是10%,其中正确的个数有( )
?
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
9.某汽车从甲地以速度v1匀速行驶至乙地后,又从乙地以速度v2匀速返回甲地,则汽车在整个行驶过程中的平均速度为( )
A.?????????????B.??????????C.??????????????D.?
10.如图是甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是(???)
A.?甲户比乙户多?????????????B.?乙户比甲户多?????????????C.?甲、乙两户一样多?????????????D.?无法确定哪一户多
二、填空题(共10题;共13分)
11.分析下列四种调查:①了解我们学校所有八年级学生的视力状况;②估计小明家一年总用电量;③登飞机前,对所有旅客进行安全检查;④了解中小学生的主要娱乐方式;其中应作普查的是:________(填序号)
12.某县有80万人口,其中各民族所占比例如上图所示,则该县少数民族
人口共有________万人.
13.空气是由多种气体混合而成的,教师为了简明扼要的向学生介绍空气的
组成情况,使用________?统计图描述数据较好.
14.某校九年级准备开展春季研学活动,对全年级学生各自最想去的活动地点进行了调查,把调查结果制成了如下扇形统计图,则“世界之窗”对应扇形的圆心角为________度.
15.将容量为n的样本中的数据分成6组,绘制频率分布直方图.若第一组至第六组数据的频率之比为2:3:4:6:4:1,且前三组数据的频数之和等于27,则n等于________?.
16.(2015?绥化)在2015年的体育考试中某校6名学生的体育成绩统计如图所示,这组数据的中位数是?________.
?
17.(2011?防城港)如图,是某校三个年级学生人数分布扇形统计图,则九年级学生人数所占扇形的圆心角的度数为________.
18.小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有________人.
19.新华高科技股份有限公司董事会决定今年用13亿资金投资发展项目,现有6个项目可供选择(每个项目或者被全部投资,或者不被投资),各项目所需投资金额和预计年均收益如下表:
?项目 ?A ?B C D ?E ?F
投资(亿元) ?5 ?2 ?6 ?4 ?6 ?8
?收益(亿元) ?0.55 ?0.4 0.6 ?0.4 ?0.9 ?1
如果要求所有投资的项目的收益总额不得低于1.6亿元,那么,当选择的投资项目是________?时,投资的收益总额最大.
20.为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(Ⅰ)被抽样调查的学生有 ________?人,并补全条形统计图________?;
(Ⅱ)每天户外活动时间的中位数是?________? (小时);
(Ⅲ)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有________?人?
三、综合题(共5题;共69分)
21.在2015年的政府工作报告中提出了九大热词,某数学兴趣小组就A互联网+、B民生底线、C中国制造2.0、D能耗强度等四个热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了________名同学;
(2)条形统计图中,m=________,n=________;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是________;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
22.(2015?资阳)学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了___名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
23.“知识改变命运,科技繁荣祖国”,某区中小学每年都要举办一届科技比赛,如图为某区某校2017年参加科技比赛(包括电子百拼、航模、机器人、建模四个类别)的参赛人数统计图.
(1)该校参加机器人、建模比赛的人数分别是________人和________人;
(2)该校参加科技比赛的总人数是________人,电子百拼所在扇形的圆心角的度数是________°,并把条形统计图补充完整;
(3)从全区中小学参加科技比赛选手中随机抽取85人,其中有34人获奖.2017年某区中小学参加科技比赛人数共有3625人,请你估算2017年参加科技比赛的获奖人数约是多少人?
24.为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2.
(1)该班共有多少名学生?
(2)请在图1中将“乒乓球”部分的图形补充完整;
(3)若全年级共有1200名学生,估计全年级参加乒乓球活动的学生有多少名?
(4)求出扇形统计图中表示“足球”的扇形的圆心角度数.
25.“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少.
答案解析部分
一、单选题
1.【答案】A
【解析】A一种灯泡有很多,数量很庞大,了解它的使用寿命时宜采用抽样的方法,所以A错误;
B众数在一组数据中若存在,可以有一个,也可有有两个、三个,所以B正确;
根据方差的意义,方差反映的是一组数据的波动大小,所以C正确;
D对于简单随机样本,总体数目不大,我们可以用样本的方差去估计总体的方差,所以D正确。
2.【答案】D
【解析】解:A、由横坐标看出4:00气温最低是24℃,故A正确;
B、由纵坐标看出6:00气温为24℃,故B正确;
C、由横坐标看出14:00气温最高31℃;
D、由横坐标看出气温是30℃的时刻是12:00,16:00,故D错误;
故选:D.
根据观察函数图象的横坐标,可得时间,根据观察函数图象的纵坐标,可得气温.
3.【答案】C
【解析】解:A、数量较大,具有破坏性,适合抽查;
B、数量较大,具有破坏性,适合抽查;
C、事关重大,因而必须进行全面调查;
D、数量较大,不容易普查,适合抽查.
故选C.
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
4.【答案】D
【解析】解:∵两校的人数不能确定,
∴通过扇形统计图无法比较女生人数的多少.
故选D.
根据扇形统计图的特点进行解答即可.
5.【答案】C
【解析】解:130÷65%=200(名),
200﹣130﹣50=20(名),
3000×=300(名),
答:该校3000名学生中持反对态度的人数约有300人,
故选:C.
根据赞成是130人,占65%即可求得总人数,利用总人数减去另外两项的人数,求得反对的人数,利用3000乘以持反对态度的比例即可.
6.【答案】A
【解析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
从小到大排列此数据为:23.5、24、24、24.5、24.5、25、25、25、25、25、26,
数据25出现了五次最多为众数.
25处在第6位为中位数.所以中位数是25,众数是25.
故选A.
7.【答案】B
【解析】解:A、一组数据2,2,3,4,这组数据的中位数是2.5,不符合题意;
B、了解一批灯泡的使用寿命的情况,适合抽样调查,符合题意;
C、小明的三次数学成绩是126分,130分,136分,则小明这三次成绩的平均数是130 分,不符合题意;
D、某日最高气温是7℃,最低气温是-2℃,则改日气温的极差是7-(-2)=9℃,不符合题意;
故答案为:B.
根据中位数的定义,一组数据从小到大排列后,处于最中间位置的数就是中位数,如果这组数据的个数是偶数个,则处于中间位置的两个数的平均数就是该组数据的中位数;抽样调查适合于要求的数据不是那么精准,具有破坏性,等的调查;根据平均数的计算方法,把该组数据的总和除以该组数据的个数即可得出该组数据的平均数;求一天温差就是用当天的最高温度减去最低温度,根据有理数的减法法则即可得出答案。
8.【答案】D
【解析】解:①2007年绿地面积比2006年增长=9%,正确;
②2008年的年增长率是≈11%>9%,所以比2007年的年增长率大,正确;
③这两年绿地面积的年平均增长率是=10%,正确.
故选D.
解决本题需要从统计图获取信息,由此关键是明确图表中数据的来源及所表示的意义,依据所示的实际意义获取正确的信息.
9.【答案】D
【解析】解:设两地距离为S,从甲地行驶至乙地的时间为T1 , 从乙地返回甲地的时间为T2 ,
则有T1=, T2=;
∴平均速度===;
故本题选D.
由题意知,设两地距离为S,从甲地行驶至乙地的时间为T1 , 从乙地返回甲地的时间为T2 , 则关键时间的计算公式求得T1及T2 , 再关键平均速度的计算公式即可求得平均速度.
10.【答案】D
【解析】根据扇形统计图的特征分析即可.
不知道甲、乙两户居民家庭全年支出的总费用,只知道百分比,无法确定哪一户多,故选D.
二、填空题
11.【答案】③
【解析】根据普查的特征,易得③,其余选用抽样调查合适.
普查适合于工作量比较小,不具有破坏性,对调查结果要求比较精确等的调查,根据普查的意义即可一一判断。
12.【答案】12
【解析】80×(8%+4%+3%)
=80×15%
=12(万人)
故答案为:12
把总人数看作单位“1”,用总人数乘少数民族所占的分率和即可求出少数民族的人口数.
13.【答案】扇形
【解析】解:根据题意,得
要直观的、简明扼要的向学生介绍空气的组成情况,即所占的比例,应选用扇形统计图.
扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
14.【答案】90
【解析】解:“世界之窗”对应扇形的圆心角=360°×(1-10%-30%-20%-15%)=90°,
故答案为:90.
“世界之窗”对应扇形的圆心角的度数=360°世界之窗”所占的百分比,计算即可。
15.【答案】60
【解析】解:设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x,x,?则2x+3x+4x+6x+4x+x=1,
?解得 ,
?所以前三组数据的频率分别是 ,
?故前三组数据的频数之和等于 =27,
?解得n=60.故答案为60.
根据题意得到第一组至第六组数据的频率之和是1,得到前三组数据的频率分别是2÷20,3÷20,4÷20;由前三组数据的频数之和等于27,求出样本容量n的值.
16.【答案】26
【解析】解:把这组数据从小到大排列,最中间两个数的平均数是(26+26)÷2=26,则中位数是26.
故答案为:26.
根据中位数的定义,即可解答.
17.【答案】144°
【解析】解:由图可知九年级学生人数所占扇形统计图的百分比为:1﹣35%﹣25%=40%,
∴九年级学生人数所占扇形的圆心角的度数为360×40%=144°,
故答案为144°.
先根据图求出九年级学生人数所占扇形统计图的百分比为40%,又知整个扇形统计图的圆心角为360度,再由360乘以40%即可得到答案.
18.【答案】10
【解析】解:全班的人数是:20÷40%=50(人), AB型的所占的百分比是: =10%,
则O型血的人数是:50(1﹣40%﹣30%﹣10%)=10(人).
故答案为:10.
根据A型血的有20人,所占的百分比是40%即可求得班级总人数,根据AB型所对应的扇形圆心角的度数求得对应的百分比,则用总人数乘以O型血所对应的百分比即可求解.
19.【答案】A、B、E
【解析】解:A:=0.11,B:=0.2,C:, D:=0.1,E:=0.15,F:=0.125
收益从大到小依次是:B>F>E>A>C=D
又∵总投资不能超过13亿,收益总额不低于1.6亿,
∴只有A,B,E比较符合要求
故选:A,B,E
分别求出收益与投资的比例,结合总投资不能超过13亿,收益总额不低于1.6亿,可求出.
20.【答案】500;;1;800
【解析】解:(Ⅰ)∵0.5小时的有100人占被调查总人数的20%,
∴被调查的人数有:100÷20%=500,
1.5小时的人数有:500﹣100﹣200﹣80=120,
补全的条形统计图如下图所示,
故答案为:500;(Ⅱ)由(1)可知被调查学生500人,由条形统计图可得,中位数是1小时,
故答案为:1;(Ⅲ)由题意可得,
该校每天户外活动时间超过1小时的学生数为: ×2000=800人,
即该校每天户外活动时间超过1小时的学生有800人.
(Ⅰ)根据条形统计图和扇形统计图可以求得被调查学生总数和1.5小时的学生数,从而可以将条形统计图补充完整;(Ⅱ)根据条形统计图可以得到这组数据的中位数;(Ⅲ)根据条形统计图可以求得校共有2000名学生,该校每天户外活动时间超过1小时的学生有多少人.
三、综合题
21.【答案】(1)300
(2)60;90
(3)72°
(4)解: . 答:从该校学生中随机抽取一个最关注热词D的学生的概率是
【解析】解:(1.)105÷35%=300(人). 故答案为:300;
(2.)n=300×30%=90(人),m=300﹣105﹣90﹣45=60(人).
故答案为:60,90;
(3.) ×360°=72°.
故答案为:72°;
(1)根据A的人数为105人,所占的百分比为35%,求出总人数,即可解答;(2)C所对应的人数为:总人数×30%,B所对应的人数为:总人数﹣A所对应的人数﹣C所对应的人数﹣D所对应的人数,即可解答;(3)根据B所占的百分比×360°,即可解答;(4)根据概率公式,即可解答.
22.【答案】(1)解:根据题意得:王老师一共调查学生:(2+1)÷15%=20(名);
故答案为:20;
(2)解:∵C类女生:20×25%﹣2=3(名);D类男生:20×(1﹣15%﹣50%﹣25%)﹣1=1(名);
如图:
(3)解:列表如下:A类中的两名男生分别记为A1和A2,
男A1 男A2 …(7分)
女A
男D 男A1男D 男A2男D 女A男D
女D 男A1女D 男A2女D 女A女D
共有6种等可能的结果,其中,一男一女的有3种,所以所选两位同学恰好是一位男生和一位女生的概率为:=.
【解析】(1)由题意可得:王老师一共调查学生:(2+1)÷15%=20(名);
(2)由题意可得:C类女生:20×25%﹣2=3(名);D类男生:20×(1﹣15%﹣50%﹣25%)﹣1=1(名);继而可补全条形统计图;
(3)首先根据题意列出表格,再利用表格求得所有等可能的结果与恰好选中一名男生和一名女生的情况,继而求得答案.
23.【答案】(1)4.;6.
(2)24.;120.
(3)解:34÷85=0.4,
0.4×3625=1450(人).
答:今年参加科技比赛比赛的获奖人数约是1450人.
【解析】解:(1)由条形统计图可得:该校参加机器人、建模比赛的人数分别是4人,6人,
故答案为:4人,6人.
(2)该校参加科技比赛的总人数是:6÷25%=24,
电子百拼所在扇形的圆心角的度数是:(24﹣6﹣6﹣4)÷24×360°=120°,
故答案为:24,120°.
条形统计图补充如下:
(1)由条形统计图即可得该校参加机器人、建模比赛的人数.
(2)由条形统计图和扇形统计图可得建模的人数和百分比,再根据总数=频数÷频率即可得出该校参加科技比赛的总人数.
(3)根据频率=频数÷总数,再用频数=总数×频率即可得出今年参加科技比赛比赛的获奖人数.
24.【答案】(1)解:20÷0.4=50(名)
(2)解:乒乓球”部分的人数是:50-15-10-20=5
(3)解:参加乒乓球活动的学生是:1200× =120(名)
(4)解:360°× =72°
【解析】(1)根据统计图中篮球的人数和百分比求出该班共有的学生数;(2)由(1)中的总人数求出“乒乓球”的人数,补全统计图;(3)由(1)(2)求出乒乓球的百分比,求出全年级参加乒乓球活动的学生的人数;(4)根据足球的百分比求出“足球”的扇形的圆心角度数.
25.【答案】(1)解:家长总数:200÷50%=400名, 表示“无所谓”人数:400﹣200﹣16﹣400×26%=80名,补全图①,
(2)解:80÷400×360°=72°
(3)解:16÷400=
【解析】(1)由图象可以得出基本赞成的有200人占50%,可以求出总数,由总数可以求出非常赞成的人数和无所谓的人数.(2)由(1)的总数求出无所谓的百分比再乘以360°就可以求出圆心角的度数.(3)这次受调查的家长不赞成的人数除以总数就是抽到恰好是“不赞成”态度的家长的概率.
(
第
1
页
共
16
页
)
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
