【专题突破训练】冀教版九年级数学上册《第26章解直角三角形》单元检测试卷(含答案)
文档属性
| 名称 | 【专题突破训练】冀教版九年级数学上册《第26章解直角三角形》单元检测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 124.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-24 19:30:02 | ||
图片预览


文档简介
【专题突破训练】冀教版九年级数学上册 第26章 解直角三角形 单元检测试卷
一、单选题(共10题;共30分)
1.在Rt△ABC中,∠C=90o,AB=10,AC=8,则sinA的值是()
A.?
4
5
??????????????????????????????????????????B.?
3
5
??????????????????????????????????????????C.?
3
4
??????????????????????????????????????????D.?
4
3
2.在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为( ??)
A.?
5
13
??????????????????????????????????????/B.?
12
13
??????????????????????????????????????/C.?
5
12
??????????????????????????????????????/D.?
12
5
?
3.△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,且c2﹣4ac+4a2=0,则sinA+cosA的值为(?? )
A.?
1+
3
2
??????????????????????????????????/B.?
1+
2
2
??????????????????????????????????/C.?
2
+
3
2
??????????????????????????????????/D.?
2
4.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为(????).
A.?7sin35°?????????????????????????????/B.?
7
cos35°
?????????????????????????????/C.?7cos35°?????????????????????????????/D.?7tan35°
5.如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,则cosB的值为 /
A.?
5
4
??????????????????????????????????????????B.?
5
3
??????????????????????????????????????????C.?
4
5
??????????????????????????????????????????D.?
3
5
6.数学实践探究课中,老师布置同学们测量学校旗杆的高度.如图所示,小明所在的学习小组在距离旗杆底部10米的地方,用测角仪测得旗杆顶端的仰角为60°,则旗杆的高度是( )米. /
A.??10?
2
??????????????????????????????????/B.?20???????????????????????????????????/C.?
10
3
3
??????????????????????????????????/D.?10
3
7.在正方形网格中,△ABC的位置如图所示,则cosB的值为(?? ) /
A.?
1
2
???????????????????????????????????????/B.?
2
2
???????????????????????????????????????/C.?
3
2
???????????????????????????????????????/D.?
3
3
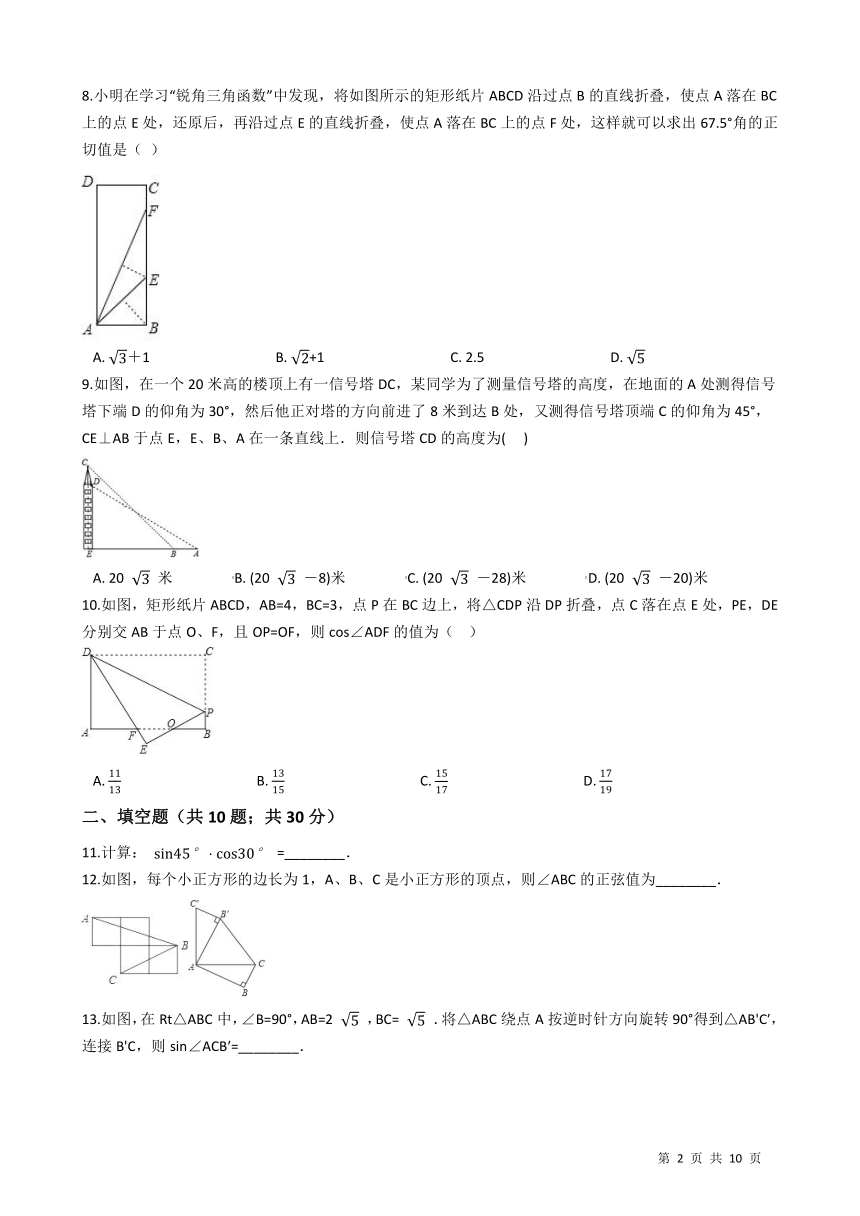
8.小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( ) /
A.?
3
+1????????????????????????????????????/B.?
2
+1????????????????????????????????????/C.?2.5????????????????????????????????????/D.?
5
9.如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为(??? )
/
A.?20
3
米?????????????????/B.?(20
3
-8)米?????????????????/C.?(20
3
-28)米?????????????????/D.?(20
3
-20)米
10.如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为(?? ) /
A.?
11
13
???????????????????????????????????????/B.?
13
15
???????????????????????????????????????/C.?
15
17
???????????????????????????????????????/D.?
17
19
二、填空题(共10题;共30分)
11.计算: sin45°?cos30° =________.
12.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为________. //
13.如图,在Rt△ABC中,∠B=90°,AB=2
5
,BC=
5
.将△ABC绕点A按逆时针方向旋转90°得到△AB'C′,连接B'C,则sin∠ACB′=________.
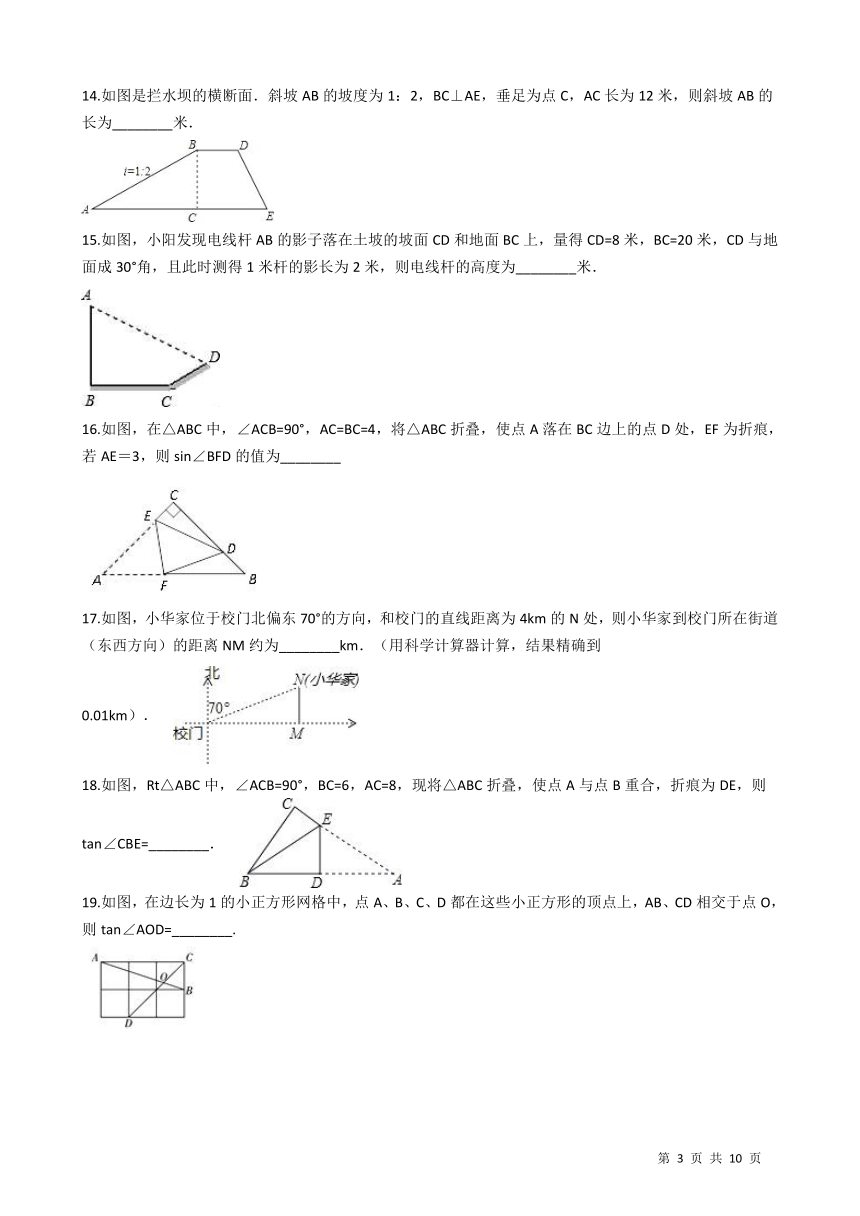
14.如图是拦水坝的横断面.斜坡AB的坡度为1:2,BC⊥AE,垂足为点C,AC长为12米,则斜坡AB的长为________米. /
15.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为________米. /
16.如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为________ /
17.如图,小华家位于校门北偏东70°的方向,和校门的直线距离为4km的N处,则小华家到校门所在街道(东西方向)的距离NM约为________km.(用科学计算器计算,结果精确到0.01km). /
18.如图,Rt△ABC中,∠ACB=90°,BC=6,AC=8,现将△ABC折叠,使点A与点B重合,折痕为DE,则tan∠CBE=________. /
19.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=________. /
20.如图,在□ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=
29
,AE=7,tan∠EAF=
5
2
,则线段BF的长为________ /
三、解答题(共8题;共60分)
21.计算:
12
?|?2|+
(1?
3
)
0
?9tan30°
22.如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和30°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.(结果保留根号) /
23.如图,在△ABC中,∠BCA=90°,BC=1.5,点F,A,C在同一直线上,∠BAC=30°,DE⊥AB于点D,BE与AB的夹角∠EBD=60°,AD=1,过E点作AC的垂线,交AC的反向延长线于F.求BE及EF的长.
/
24.小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)(参考数据:sin37°≈
3
5
,tan37°≈
3
4
,sin48°≈
7
10
,tan48°≈
11
10
) /
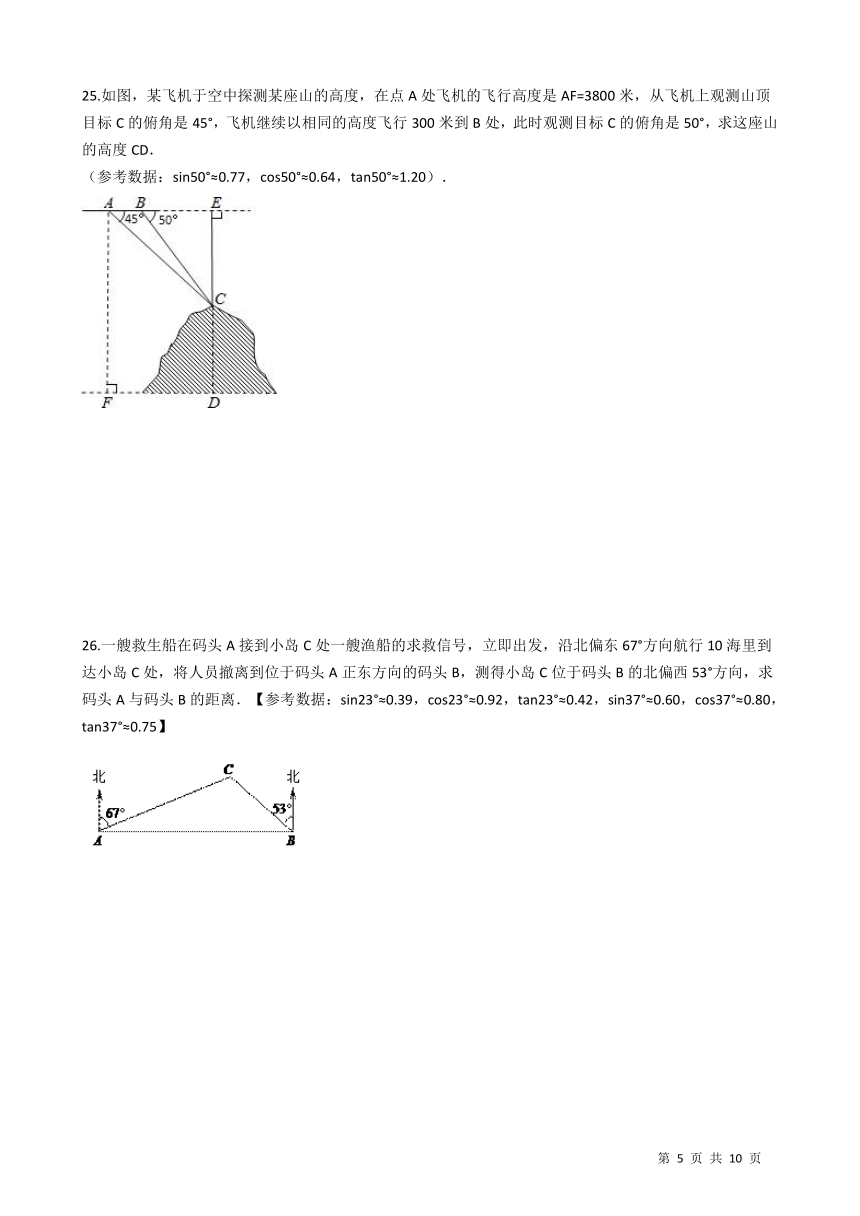
25.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3800米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD. (参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20). /
26.一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,测得小岛C位于码头B的北偏西53°方向,求码头A与码头B的距离.【参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.42,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】 /
27.如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据: /≈1.41). /
28.某市开展一项自行车旅游活动,线路需经A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,
2
≈1.4,
3
≈1.7 ) /
答案解析部分
一、单选题
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】C
二、填空题
11.【答案】
6
4
?
12.【答案】
2
2
13.【答案】
4
5
14.【答案】6
5
.
15.【答案】14+2
3
16.【答案】
1
3
17.【答案】1.37
18.【答案】
7
24
19.【答案】2
20.【答案】
13
5
三、解答题
21.【答案】 -1-
3
22.【答案】解:如图,过点A作AD⊥BC于点D, / 根据题意可得,∠DAB=∠BAC=∠C=30°,BC=100m, ∴AB=BC=100m, 在Rt△ADB中,AB=100m,∠DAB =30°, ∴AD=cos30°·AB=
3
2
×100 =50
3
m. 答:热气球离地面的高度为50
3
m
23.【答案】解:如图,过点B作BH⊥EF于H.
/
∵在Rt△ABC中,∠BAC=30°,BC=1.5,
∴AB=3.又∵AD=1,∴BD=2.∵ED⊥AB,∠DBE=60°,∴在Rt△DBE中,cos ∠DBE=
????
????
=
1
2
∴BE=4.∵∠BCA=∠BHF=∠HFC=90°,∴四边形HFCB为矩形.
∴HF=BC=1.5,CF∥BH.∴∠HBA=∠BAC=30°.∴∠EBH=∠EBD-∠HBA=30°.
∴在Rt△EBH中,EH=
1
2
BE=2.∴EF=EH+HF=2+1.5=3.5.
24.【答案】解:设CD = x米,在Rt△ACD中, tan37°=
????
????
, 则
3
4
=
????
??
, ∴.AD=
3
4
x 在Rt△BCD中, tan48° =
????
????
, 则
11
10
=
????
??
, ∴. BD=
11
10
x ∵AD+BD = AB, ∴
3
4
x+
11
10
x=80. 解得:x≈43. 答:小明家所在居民楼与大厦的距离CD大约是43米.
25.【答案】解:设EC=x, 在Rt△BCE中,tan∠EBC=
????
????
, 则BE=
????
??????∠??????
=
5
6
x, 在Rt△ACE中,tan∠EAC=
????
????
, 则AE=
????
??????∠??????
=x, ∵AB+BE=AE, ∴300+
5
6
x=x, 解得:x=1800, 这座山的高度CD=DE﹣EC=3800﹣1800=2000(米). 答:这座山的高度是2000米.
26.【答案】解:过点C作CD⊥AB,垂足为D,由题意得∠CAD=23°, / ∠CBD=37°, 在Rt△ACD中, ∵sin∠CAD=
????
????
, ∴CD=sin∠CAD·AC=0.39×10=3.9, ∵cos∠CAD=
????
????
, ∴AD=cos∠CAD·AC=0.92×10=9.2 . 在Rt△CDB中, ∵tan∠CBD=
????
????
, ∴DB=
????
tan∠??????
=
3.9
0.75
=5.2 , ∴AB=AD+BD=9.2+5.2=14.4 . 答:码头A与码头B相距14.4海里.
27.【答案】解:作EF⊥AC, / 根据题意,CE=18×15=270米, ∵tan∠CED=1, ∴∠CED=∠DCE=45°, ∵∠ECF=90°-45°-15°=30°, ∴EF=
1
2
CE=135米, ∵∠CEF=60°,∠AEB=30°, ∴∠AEF=180°-45°-60°-30°=45°, ∴AE=135
2
∴AB=
1
2
×135
2
≈95.2米.
28.【答案】解:由题意可知∠DCA=180°﹣75°﹣45°=60°, ∵BC=CD, ∴△BCD是等边三角形. 过点B作BE⊥AD,垂足为E,如图所示: / 由题意可知∠DAC=75°﹣30°=45°, ∵△BCD是等边三角形, ∴∠DBC=60° BD=BC=CD=20km, ∴∠ADB=∠DBC﹣∠DAC=15°, ∴BE=sin15°BD≈0.25×20≈5m, ∴AB=
????
??????45°
=
5
2
2
≈7m, ∴AB+BC+CD≈7+20+20≈47m. 答:从A地跑到D地的路程约为47m.
一、单选题(共10题;共30分)
1.在Rt△ABC中,∠C=90o,AB=10,AC=8,则sinA的值是()
A.?
4
5
??????????????????????????????????????????B.?
3
5
??????????????????????????????????????????C.?
3
4
??????????????????????????????????????????D.?
4
3
2.在Rt△ABC中,∠C=90°,AB=13,AC=5,则sinA的值为( ??)
A.?
5
13
??????????????????????????????????????/B.?
12
13
??????????????????????????????????????/C.?
5
12
??????????????????????????????????????/D.?
12
5
?
3.△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,且c2﹣4ac+4a2=0,则sinA+cosA的值为(?? )
A.?
1+
3
2
??????????????????????????????????/B.?
1+
2
2
??????????????????????????????????/C.?
2
+
3
2
??????????????????????????????????/D.?
2
4.在Rt△ABC中,∠C=90°,∠B=35°,AB=7,则BC的长为(????).
A.?7sin35°?????????????????????????????/B.?
7
cos35°
?????????????????????????????/C.?7cos35°?????????????????????????????/D.?7tan35°
5.如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,则cosB的值为 /
A.?
5
4
??????????????????????????????????????????B.?
5
3
??????????????????????????????????????????C.?
4
5
??????????????????????????????????????????D.?
3
5
6.数学实践探究课中,老师布置同学们测量学校旗杆的高度.如图所示,小明所在的学习小组在距离旗杆底部10米的地方,用测角仪测得旗杆顶端的仰角为60°,则旗杆的高度是( )米. /
A.??10?
2
??????????????????????????????????/B.?20???????????????????????????????????/C.?
10
3
3
??????????????????????????????????/D.?10
3
7.在正方形网格中,△ABC的位置如图所示,则cosB的值为(?? ) /
A.?
1
2
???????????????????????????????????????/B.?
2
2
???????????????????????????????????????/C.?
3
2
???????????????????????????????????????/D.?
3
3
8.小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°角的正切值是( ) /
A.?
3
+1????????????????????????????????????/B.?
2
+1????????????????????????????????????/C.?2.5????????????????????????????????????/D.?
5
9.如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达B处,又测得信号塔顶端C的仰角为45°,CE⊥AB于点E,E、B、A在一条直线上.则信号塔CD的高度为(??? )
/
A.?20
3
米?????????????????/B.?(20
3
-8)米?????????????????/C.?(20
3
-28)米?????????????????/D.?(20
3
-20)米
10.如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为(?? ) /
A.?
11
13
???????????????????????????????????????/B.?
13
15
???????????????????????????????????????/C.?
15
17
???????????????????????????????????????/D.?
17
19
二、填空题(共10题;共30分)
11.计算: sin45°?cos30° =________.
12.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为________. //
13.如图,在Rt△ABC中,∠B=90°,AB=2
5
,BC=
5
.将△ABC绕点A按逆时针方向旋转90°得到△AB'C′,连接B'C,则sin∠ACB′=________.
14.如图是拦水坝的横断面.斜坡AB的坡度为1:2,BC⊥AE,垂足为点C,AC长为12米,则斜坡AB的长为________米. /
15.如图,小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为________米. /
16.如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为________ /
17.如图,小华家位于校门北偏东70°的方向,和校门的直线距离为4km的N处,则小华家到校门所在街道(东西方向)的距离NM约为________km.(用科学计算器计算,结果精确到0.01km). /
18.如图,Rt△ABC中,∠ACB=90°,BC=6,AC=8,现将△ABC折叠,使点A与点B重合,折痕为DE,则tan∠CBE=________. /
19.如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=________. /
20.如图,在□ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=
29
,AE=7,tan∠EAF=
5
2
,则线段BF的长为________ /
三、解答题(共8题;共60分)
21.计算:
12
?|?2|+
(1?
3
)
0
?9tan30°
22.如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和30°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.(结果保留根号) /
23.如图,在△ABC中,∠BCA=90°,BC=1.5,点F,A,C在同一直线上,∠BAC=30°,DE⊥AB于点D,BE与AB的夹角∠EBD=60°,AD=1,过E点作AC的垂线,交AC的反向延长线于F.求BE及EF的长.
/
24.小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)(参考数据:sin37°≈
3
5
,tan37°≈
3
4
,sin48°≈
7
10
,tan48°≈
11
10
) /
25.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3800米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD. (参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20). /
26.一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到位于码头A正东方向的码头B,测得小岛C位于码头B的北偏西53°方向,求码头A与码头B的距离.【参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.42,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】 /
27.如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据: /≈1.41). /
28.某市开展一项自行车旅游活动,线路需经A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,
2
≈1.4,
3
≈1.7 ) /
答案解析部分
一、单选题
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】C
二、填空题
11.【答案】
6
4
?
12.【答案】
2
2
13.【答案】
4
5
14.【答案】6
5
.
15.【答案】14+2
3
16.【答案】
1
3
17.【答案】1.37
18.【答案】
7
24
19.【答案】2
20.【答案】
13
5
三、解答题
21.【答案】 -1-
3
22.【答案】解:如图,过点A作AD⊥BC于点D, / 根据题意可得,∠DAB=∠BAC=∠C=30°,BC=100m, ∴AB=BC=100m, 在Rt△ADB中,AB=100m,∠DAB =30°, ∴AD=cos30°·AB=
3
2
×100 =50
3
m. 答:热气球离地面的高度为50
3
m
23.【答案】解:如图,过点B作BH⊥EF于H.
/
∵在Rt△ABC中,∠BAC=30°,BC=1.5,
∴AB=3.又∵AD=1,∴BD=2.∵ED⊥AB,∠DBE=60°,∴在Rt△DBE中,cos ∠DBE=
????
????
=
1
2
∴BE=4.∵∠BCA=∠BHF=∠HFC=90°,∴四边形HFCB为矩形.
∴HF=BC=1.5,CF∥BH.∴∠HBA=∠BAC=30°.∴∠EBH=∠EBD-∠HBA=30°.
∴在Rt△EBH中,EH=
1
2
BE=2.∴EF=EH+HF=2+1.5=3.5.
24.【答案】解:设CD = x米,在Rt△ACD中, tan37°=
????
????
, 则
3
4
=
????
??
, ∴.AD=
3
4
x 在Rt△BCD中, tan48° =
????
????
, 则
11
10
=
????
??
, ∴. BD=
11
10
x ∵AD+BD = AB, ∴
3
4
x+
11
10
x=80. 解得:x≈43. 答:小明家所在居民楼与大厦的距离CD大约是43米.
25.【答案】解:设EC=x, 在Rt△BCE中,tan∠EBC=
????
????
, 则BE=
????
??????∠??????
=
5
6
x, 在Rt△ACE中,tan∠EAC=
????
????
, 则AE=
????
??????∠??????
=x, ∵AB+BE=AE, ∴300+
5
6
x=x, 解得:x=1800, 这座山的高度CD=DE﹣EC=3800﹣1800=2000(米). 答:这座山的高度是2000米.
26.【答案】解:过点C作CD⊥AB,垂足为D,由题意得∠CAD=23°, / ∠CBD=37°, 在Rt△ACD中, ∵sin∠CAD=
????
????
, ∴CD=sin∠CAD·AC=0.39×10=3.9, ∵cos∠CAD=
????
????
, ∴AD=cos∠CAD·AC=0.92×10=9.2 . 在Rt△CDB中, ∵tan∠CBD=
????
????
, ∴DB=
????
tan∠??????
=
3.9
0.75
=5.2 , ∴AB=AD+BD=9.2+5.2=14.4 . 答:码头A与码头B相距14.4海里.
27.【答案】解:作EF⊥AC, / 根据题意,CE=18×15=270米, ∵tan∠CED=1, ∴∠CED=∠DCE=45°, ∵∠ECF=90°-45°-15°=30°, ∴EF=
1
2
CE=135米, ∵∠CEF=60°,∠AEB=30°, ∴∠AEF=180°-45°-60°-30°=45°, ∴AE=135
2
∴AB=
1
2
×135
2
≈95.2米.
28.【答案】解:由题意可知∠DCA=180°﹣75°﹣45°=60°, ∵BC=CD, ∴△BCD是等边三角形. 过点B作BE⊥AD,垂足为E,如图所示: / 由题意可知∠DAC=75°﹣30°=45°, ∵△BCD是等边三角形, ∴∠DBC=60° BD=BC=CD=20km, ∴∠ADB=∠DBC﹣∠DAC=15°, ∴BE=sin15°BD≈0.25×20≈5m, ∴AB=
????
??????45°
=
5
2
2
≈7m, ∴AB+BC+CD≈7+20+20≈47m. 答:从A地跑到D地的路程约为47m.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
