沪科版九年级下册第24章圆检测卷(含答案)
文档属性
| 名称 | 沪科版九年级下册第24章圆检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 435.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-26 08:27:01 | ||
图片预览


文档简介
第24章检测卷
(120分钟 150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
B
D
D
C
B
C
C
B
A
B
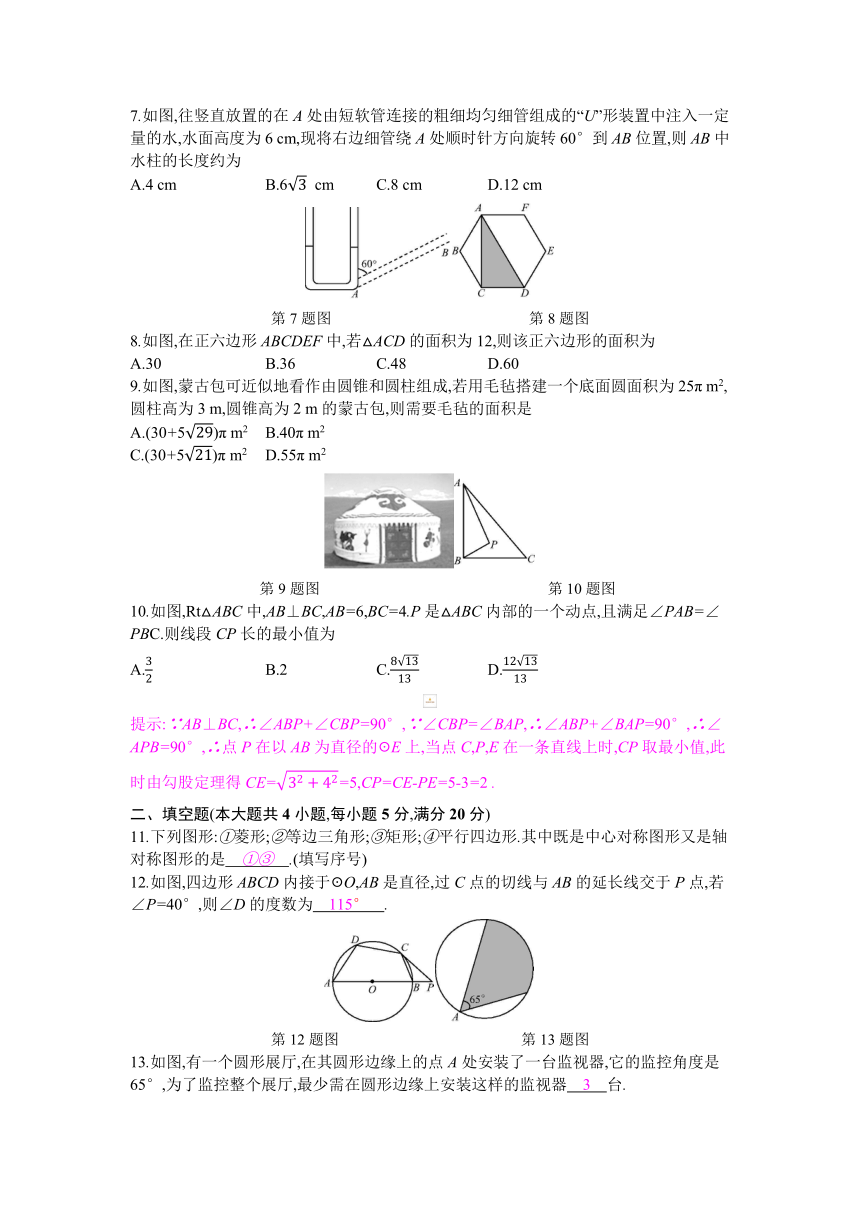
1.将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是
/
2.如图,已知圆心角∠AOB=110°,则圆周角∠ACB=
/
A.55° B.110° C.120° D.125°
3.下列说法正确的是
A.三角形的内心到三角形三个顶点的距离相等
B.三点确定一个圆
C.平分弦的直径垂直于弦
D.同圆或等圆中,相等的弧所对的圆心角相等
4.如图,圆上有A,B,C,D四点,圆内有E,F两点且点E,F在BC上.若四边形AEFD为正方形,则下列弧长关系中,正确的是
A.
????
<
????
B.
????
=
????
C.
????
<
????
D.
????
=
????
//
第4题图 第5题图
5.如图,一段公路的转弯处是一段圆弧(
????
),则
????
的长度为
A.3π B.6π C.9π D.12π
6.在△ABC中,AC=3,CB=4,以C为圆心r为半径作圆,如果点A、点B只有一个点在圆内,那么半径r的取值范围是
A.r>3 B.r≥4 C.3
A.4 cm B.6
3
cm C.8 cm D.12 cm
//
第7题图 第8题图
8.如图,在正六边形ABCDEF中,若△ACD的面积为12,则该正六边形的面积为
A.30 B.36 C.48 D.60
9.如图,蒙古包可近似地看作由圆锥和圆柱组成,若用毛毡搭建一个底面圆面积为25π m2,圆柱高为3 m,圆锥高为2 m的蒙古包,则需要毛毡的面积是
A.(30+5
29
)π m2 B.40π m2
C.(30+5
21
)π m2 D.55π m2
//
第9题图 第10题图
10.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4.P是△ABC内部的一个动点,且满足∠PAB=∠PBC.则线段CP长的最小值为
A.
3
2
B.2 C.
8
13
13
D.
12
13
13
/
提示:∵AB⊥BC,∴∠ABP+∠CBP=90°,∵∠CBP=∠BAP,∴∠ABP+∠BAP=90°,∴∠APB=90°,∴点P在以AB为直径的☉E上,当点C,P,E在一条直线上时,CP取最小值,此时由勾股定理得CE=
3
2
+
4
2
=5,CP=CE-PE=5-3=2 .
二、填空题(本大题共4小题,每小题5分,满分20分)
11.下列图形:①菱形;②等边三角形;③矩形;④平行四边形.其中既是中心对称图形又是轴对称图形的是 ①③ .(填写序号)?
12.如图,四边形ABCD内接于☉O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为 115° .?
//
第12题图 第13题图
13.如图,有一个圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它的监控角度是65°,为了监控整个展厅,最少需在圆形边缘上安装这样的监视器 3 台.?
14.已知☉O的直径CD=10 cm,AB是☉O的弦,AB⊥CD,垂足为M,且AB=8 cm,则AC的长为 2
5
cm或4
5
cm .?
三、(本大题共2小题,每小题8分,满分16分)
/
15.如图所示,AB为☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
解:连接OD.
∵AB=2DE,AB=2OD,∴OD=DE,
∴∠DOE=∠E=20°,∴∠CDO=∠DOE+∠E=40°,
∵OC=OD,∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
16.已知△ABC,求作☉O,使☉O经过△ABC的三个顶点.(不写作法,保留作图痕迹)
/
解:如图所示.
/
四、(本大题共2小题,每小题8分,满分16分)
17.如果从半径为5 cm的圆形纸片上剪去
1
5
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),求这个圆锥的高.
解:∵从半径为5 cm的圆形纸片上剪去
1
5
圆周的一个扇形,
∴留下的扇形的弧长为
4×2π×5
5
=8π cm,
根据圆锥底面圆的周长等于扇形弧长,
∴圆锥的底面半径r=
8π
2π
=4 cm,
∴圆锥的高为
5
2
-
4
2
=3 cm.
/
18.如图,E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆☉O的直径是6,求BD的长.
解:(1)∵E是△ABC的内心,
∴∠BAD=∠CAD,∠ABE=∠CBE,
∵∠CBD=∠CAD,∴∠BAD=∠CBD,
∵∠BED=∠ABE+∠BAD,
∴∠BED=∠CBE+∠CBD,
∵∠EBD=∠CBE+∠CBD,∴∠BED=∠EBD,∴ED=BD.
(2)连接CD.
∵∠BAC=90°,∴BC是☉O的直径,∴∠BDC=90°,
∵☉O的直径为6,∴BC=6,
∵E为△ABC的内切圆的圆心,
∴∠BAD=∠CAD,∴BD=DC,
∴BD=DC=
2
2
BC=3
2
.
五、(本大题共2小题,每小题10分,满分20分)
19.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,求球的半径长.
/
解:如图,取EF的中点M,作MN⊥AD交BC于点N,则MN经过球心O,连接OF.
∵四边形ABCD是矩形,∴∠C=∠D=90°,
∴四边形CDMN是矩形,∴MN=CD=4,
设OF=x,则ON=OF,
∴OM=MN-ON=4-x,MF=2,
在Rt△OMF中,OM2+MF2=OF2,
即(4-x)2+22=x2,解得x=2.5.
答:球的半径长为2.5 cm.
/
20.如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3),B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1,B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
/
解:(1)△A1B1C如图所示.
/
由A(4,3),B(4,1)可建立如图所示的平面直角坐标系,
则点A1的坐标为(-1,4),点B1的坐标为(1,4).
(2)∵AC=
??
??
2
+??
??
2
=
2
2
+
3
2
=
13
,∠ACA1=90°,
∴在旋转过程中,△ABC所扫过的面积为
??
扇形????
??
1
+S△ABC=
90π·(
13
)
2
360
+
1
2
×3×2=
13π
4
+3.
六、(本题满分12分)
/
21.如图,已知△ABC为直角三角形,∠C=90°,边BC是☉O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=
3
4
,求☉O的半径.
解:(1)连接OD.
∵BC是☉O的切线,∴OD⊥BC,∴∠ODB=90°,
又∵∠C=90°,∴AC∥OD,∴∠CAD=∠ADO,
又∵OA=OD,∴∠OAD=∠ADO,∴∠CAD=∠OAD,
∴ AD平分∠BAC.
(2)连接DE.
在Rt△ACD中,∵tan ∠DAC=
????
????
=
3
4
,AC=8,∴CD=6,
∴AD=
??
??
2
+??
??
2
=10.
∵AE为☉O的直径,∴∠ADE=90°,∴∠ADE=∠C,
∵∠CAD=∠OAD,∴△ACD∽△ADE,
∴
????
????
=
????
????
,即
10
8
=
????
10
,∴AE=
25
2
,∴☉O的半径是
25
4
.
七、(本题满分12分)
/
22.如图,☉O是正五边形ABCDE的外接圆,F是
????
的中点,连接CF,EF.
(1)请直接写出∠CFE= 72 °;?
(2)求证:EF=CF;
(3)若☉O的半径为5,求
????
的长.
解:(2)∵五边形ABCDE是正五边形,∴AE=BC,∴
????
=
????
,
又∵F是
????
的中点,∴
????
=
????
,
∴
????
+
????
=
????
+
????
,∴
????
=
????
,∴EF=CF.
(3)∵☉O是正五边形ABCDE的外接圆,
∴
????
=
????
=
????
=
????
=
????
,
∵R=5,∴
??
????
=
??
????
=
1
5
×2πR=2π,
又∵
??
????
=
1
2
??
????
=π,∴
??
????
=
??
????
+
??
????
=3π.
八、(本题满分14分)
23.如图,在直角三角形ABC中,∠ACB=90°,H是△ABC的内心,
AH的延长线和△ABC的外接圆O相交于点D,连接DB.
(1)求证:DH=DB;
(2)过点D作BC的平行线交AC,AB的延长线分别于点E,F,已知CE=1,圆O的直径为5.
①求证:EF为圆O的切线;
②求DF的长.
/
解:(1)连接HB.
∵H是△ABC的内心,
∴∠DAC=∠DAB,∠ABH=∠CBH,
∵∠DBC=∠DAC,
∴∠DHB=∠DAB+∠ABH=∠DAC+∠CBH,
∵∠DBH=∠DBC+∠CBH,
∴∠DHB=∠DBH,∴DH=DB.
(2)①连接OD.∵∠DOB=2∠DAB=∠BAC,
∴OD∥AC,∵AC⊥BC,BC∥EF,
∴AC⊥EF,∴OD⊥EF,
∵点D在☉O上,∴EF是☉O的切线.
②连接CD,过点D作DG⊥AB于点G.
∵∠EAD=∠DAB,∴DE=DG,
∵DC=DB,∠CED=∠DGB=90°,
∴△CDE≌△BDG,
∴GB=CE=1,
在Rt△ADB中,DG⊥AB,∴∠DAB=∠BDG,
∵∠DBG=∠ABD,∴△DBG∽△ABD,
∴
????
????
=
????
????
,∴DB2=AB·BG=5×1=5,
∴DB=
5
,DG=2,∴ED=2,
∵H是内心,∴AE=AG=4,
∵DO∥AE,∴△OFD∽△AFE,
∴
????
????
=
????
????
,∴
????
????+2
=
5
2
4
,
∴DF=
10
3
.
