沪科版九年级下册第25章投影与视图检测卷(含答案)
文档属性
| 名称 | 沪科版九年级下册第25章投影与视图检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 654.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-26 08:26:26 | ||
图片预览

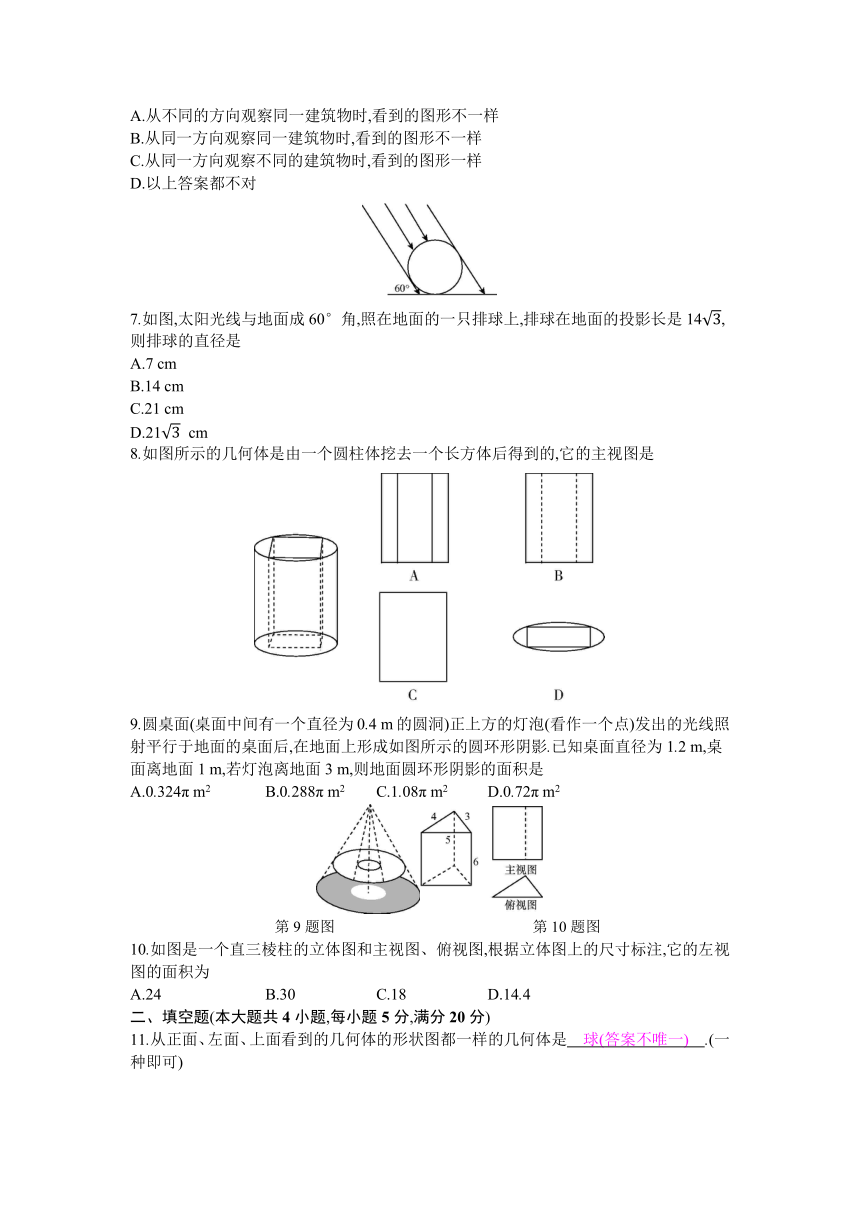
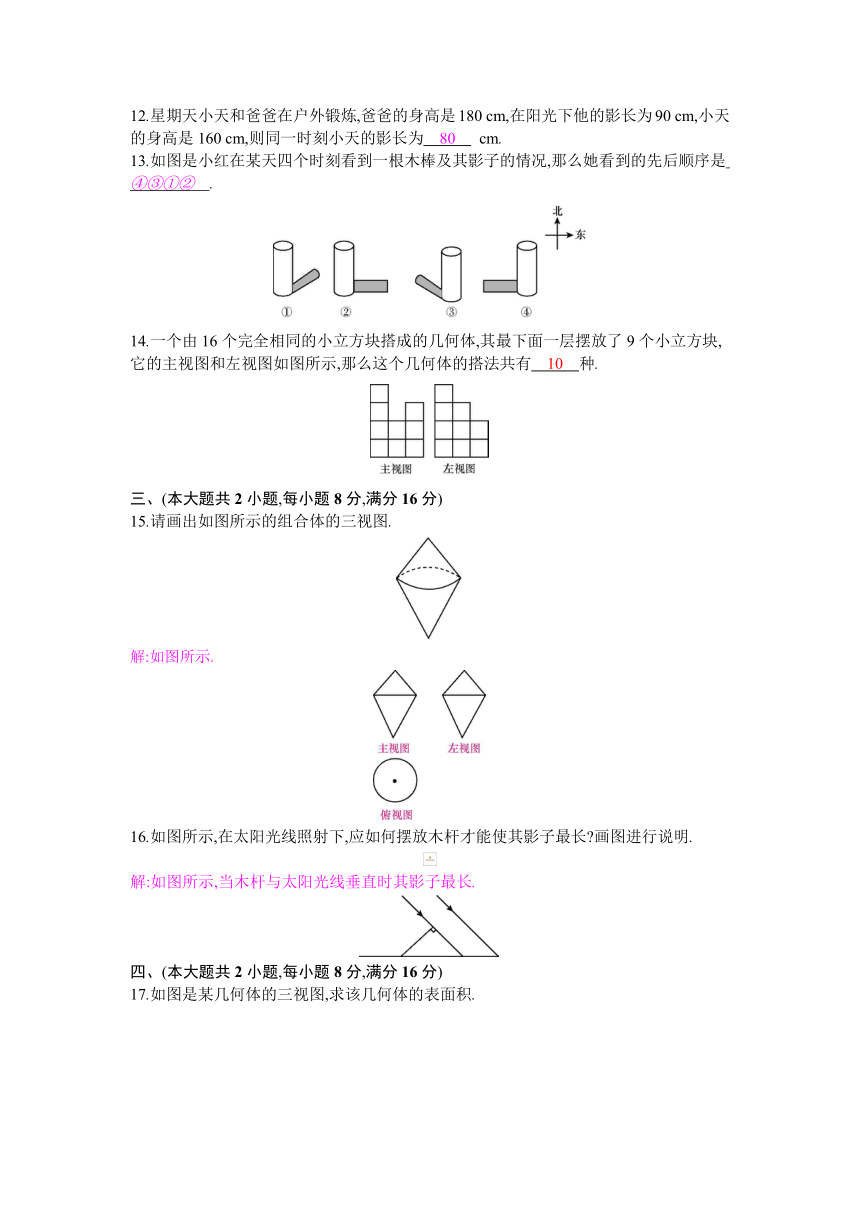
文档简介
第25章检测卷
(120分钟 150分)
一、选择题(本大题共10小题,每小题4分,满分40分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
D
B
C
A
C
A
C
B
D
D
1.下列四幅图中,表示两棵小树在同一时刻阳光下的影子的可能是
/
2.下列几何体中,主视图和俯视图都为矩形的是
/
3.今年“父亲节”佳佳给父亲送了一个礼盒,该礼盒的主视图是
/
4.如图,该几何体的俯视图是
/
5.如图是由三个相同的小正方体组成的几何体,则该几何体的左视图是
/
6.“横看成岭侧成峰”从数学的角度解释为
A.从不同的方向观察同一建筑物时,看到的图形不一样
B.从同一方向观察同一建筑物时,看到的图形不一样
C.从同一方向观察不同的建筑物时,看到的图形一样
D.以上答案都不对
/
7.如图,太阳光线与地面成60°角,照在地面的一只排球上,排球在地面的投影长是14
3
,则排球的直径是
A.7 cm
B.14 cm
C.21 cm
D.21
3
cm
8.如图所示的几何体是由一个圆柱体挖去一个长方体后得到的,它的主视图是
/
9.圆桌面(桌面中间有一个直径为0.4 m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2 m,桌面离地面1 m,若灯泡离地面3 m,则地面圆环形阴影的面积是
A.0.324π m2 B.0.288π m2 C.1.08π m2 D.0.72π m2
//
第9题图 第10题图
10.如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为
A.24 B.30 C.18 D.14.4
二、填空题(本大题共4小题,每小题5分,满分20分)
11.从正面、左面、上面看到的几何体的形状图都一样的几何体是 球(答案不唯一) .(一种即可)?
12.星期天小天和爸爸在户外锻炼,爸爸的身高是180 cm,在阳光下他的影长为90 cm,小天的身高是160 cm,则同一时刻小天的影长为 80 cm.?
13.如图是小红在某天四个时刻看到一根木棒及其影子的情况,那么她看到的先后顺序是 ④③①② .?
/
14.一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有 10 种.?
/
三、(本大题共2小题,每小题8分,满分16分)
15.请画出如图所示的组合体的三视图.
/
解:如图所示.
/
16.如图所示,在太阳光线照射下,应如何摆放木杆才能使其影子最长?画图进行说明.
/
解:如图所示,当木杆与太阳光线垂直时其影子最长.
/
四、(本大题共2小题,每小题8分,满分16分)
17.如图是某几何体的三视图,求该几何体的表面积.
/
/
解:由三视图还原几何体如图.
该几何体为组合体,下半部分是圆柱,圆柱的底面半径为5,高是20,上半部分为圆锥,底面半径为5,高为5,
则圆柱的底面积为25π,侧面积为10π×20=200π,
圆锥的侧面积为
1
2
×10π×
5
2
+
5
2
=25
2
π.
∴该几何体的表面积为(225+25
2
)π.
18.由若干小立方体叠成的几何体的三视图如图所示:
(1)分别说出A,B,C,D这4个方格位置上的小立方体的个数;
(2)这个几何体共有多少个小立方体?
/
解:(1)结合三个视图,可知A位置有2个小立方体,B位置有2个小立方体,C位置有1个小立方体,D位置有3个小立方体.
(2)结合(1)中的分析,该几何体共有两层,上层有1个小立方体,下层有4个小立方体,共有5个小立方体.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子,已知窗框的影子DE到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).
/
解:连接AB.由于阳光是平行光线,即AE∥BD,
所以∠AEC=∠BDC.
又因为∠C是公共角,所以△AEC∽△BDC,从而有
????
????
=
????
????
.
又因为AC=AB+BC,DC=EC-ED,EC=3.9,ED=2.1,BC=1.2,
所以有
????+1.2
1.2
=
3.9
3.9-2.1
,解得AB=1.4 m.
答:窗口的高度为1.4 m.
20.已知一个圆锥的三视图如图所示,求这个圆锥的侧面积和体积.
/
解:根据三视图得到圆锥的底面圆的直径为8,即底面圆的半径r为4,圆锥的高为3,
所以圆锥的母线长l=
3
2
+
4
2
=5,
所以这个圆锥的侧面积是π×4×5=20π,
体积是
1
3
π×42×3=16π.
六、(本题满分12分)
/
21.如图所示,一幢楼房AB背后有台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶MN上晒太阳.
(1)求楼房的高度约为多少米?(结果精确到0.1米)
(2)过了一会儿,当α=45°时,小猫还能不能晒到太阳?请说明理由.(参考数据:
3
≈1.732)
解:(1)当α=60°时,在Rt△ABE中,
∵tan 60°=
????
????
=
????
10
,
∴AB=10·tan 60°=10
3
≈10×1.73=17.3米.
∴楼房的高度约为17.3米.
/
(2)当α=45°时,小猫还能晒到太阳.
理由:假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为F,与MC的交点为H.
∵∠BFA=45°,∴tan 45°=
????
????
=1,
此时的影长AF=AB=17.3米,
∴CF=AF-AC=0.1米,∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫还能晒到太阳.
七、(本题满分12分)
22.有一个几何体的形状为直三棱柱,如图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.
/
解:(1)俯视图如图所示.
/
(2)由勾股定理得底面的斜边长为10 cm,
S底=
1
2
×8×6=24 cm2,S侧=(8+6+10)×3=72 cm2,
∴S全=72+24×2=120 cm2.
八、(本题满分14分)
23.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6 m的小明(AB)的影子BC长是3 m,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得HB=6 m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
(2)求路灯灯泡的垂直高度GH;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH的中点B1处时,其影子长为B1C1;当小明继续走剩下路程的
1
3
到B2处时,其影子长为B2C2;当小明继续走剩下路程的
1
4
到B3处,…,按此规律继续走下去,当小明走剩下路程的
1
??+1
到Bn处时,其影子BnCn的长为?
3
??+1
m.(直接用含n的代数式表示)?
/
解:(1)形成影子的光线如图所示,路灯灯泡所在的位置为点G.
/
(2)根据题意,得△ABC∽△GHC,∴
????
????
=
????
????
,∴
1.6
????
=
3
6+3
,解得GH=4.8 m.
答:路灯灯泡的垂直高度GH是4.8 m.
(3)提示:同理可得△A1B1C1∽△GHC1,∴
??
1
??
1
????
=
??
1
??
1
??
??
1
,
设B1C1长为x m,则
1.6
4.8
=
??
??+3
,
解得x=1.5,即B1C1=1.5 m.
同理
1.6
4.8
=
??
2
??
2
??
2
??
2
+2
,解得B2C2=1 m,
∴
1.6
4.8
=
??
??
??
??
??
??
??
??
+
1
??+1
×6
,解得BnCn=
3
??+1
.
