九年级上《第26章解直角三角形》单元试卷(含答案)
文档属性
| 名称 | 九年级上《第26章解直角三角形》单元试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 129.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-26 19:10:46 | ||
图片预览




文档简介
【期末专题复习】冀教版九年级数学上册第26章解直角三角形_单元检测试卷
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 在????△??????中,如果各边长度都扩大2倍,则锐角??的正弦值和正切值( )
A.都缩小
1
2
B.都扩大2倍
C.都没有变化
D.不能确定
?2. sin
30
°
的值是( )
A.
1
2
B.
2
2
C.
3
2
D.1
?3. 已知??、??都是锐角,且sin??A.??>??
B.tan??>tan??
C.cos??>cos??
D.??=??
?4. 如果??是锐角,则下列成立的是( )
A.sin??+cos??=1
B.sin??+cos??>1
C.sin??+cos??<1
D.sin??+cos??≤1
?5. 如图,△??????中,????=5,cos??=
2
2
,sin??=
3
5
,则△??????的面积为( )
/
A.
21
2
B.12
C.14
D.21
?6. 如图,??是∠??的边????上一点,且点??的坐标为(3,?4),则cos??=( )
/
A.
3
5
B.
4
5
C.
3
4
D.
4
3
?7. 小明(??)和小丽(??)两人一前一后放风筝,结果风筝在空中??处纠缠在一起(如示意图).若∠??????=
45
°
,小丽、小明之间的距离与小丽已用的放风筝线的长度相等,则∠??的正切值是( )
/
A.2+
3
B.2?
3
C.
2
+1
D.
2
?1
?8. 温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市??的正西方向300千米的??处(如图),以每小时10
7
千米的速度向东偏南
30
°
的????方向移动,并检测到台风中心在移动过程中,温州市??将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市??的时间会持续多长?( )
/
A.5
B.6
C.8
D.10
?
9. 一人乘雪橇沿坡比1:
3
的斜坡笔直滑下,滑下的距离??(??)与时间??(??)间的关系为??=10??+2
??
2
,若滑到坡底的时间为4??,则此人下降的高度为( )
/
A.72??
B.36
3
??
C.36??
D.18
3
??
?10. 如图,为了测得电视塔的高度????,在??处用高为1米的测角仪????,测得电视塔顶端??的仰角为
30
°
,再向电视塔方向前进120米达到??处,又测得电视塔顶端??的仰角为
60
°
,则这个电视塔的高度????(单位:米)为( )
/
A.60
3
B.61
C.60
3
+1
D.121
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?11. 求值:
sin
2
60
°
+
cos
2
60
°
=________.
?12. 如图,一艘轮船由西向东航行,在??处测得北偏东
68.7
°
反向有小岛??,继续前进60海里到达??处,此时测得小岛??在船的北偏东
26.5
°
方向,则船继续向东航行________海里,离小岛最近(精确到0.1海里,参考数据tan
21.3
°
≈0.39,tan
63.5
°
≈2.01).
/
?13. 在△??????中,∠??=
90
°
,cos??=
2
3
,则??﹕??﹕??为________.
?14. 在????△??????中,∠??=
90
°
,????=3,????=4,那么cos??的值是________.
?15. 已知在????△??????中,∠??=
90
°
,sin??=
3
5
,则tan??的值为________. ?
16. 如示意图,若斜坡????的坡度??=1:3,∠??????=
90
°
,????=23米,则????的长为________米.
/?
17. 如图,某建筑物????上有一旗杆????,从与????相距38??的??处观测旗杆顶部??的仰角为
50
°
,观测旗杆底部??的仰角为
45
°
,则旗杆的高度约为________??.(结果精确到0.1??,参考数据:sin
50
°
≈0.77,cos
50
°
≈0.64,tan
50
°
≈1.19)
/
?
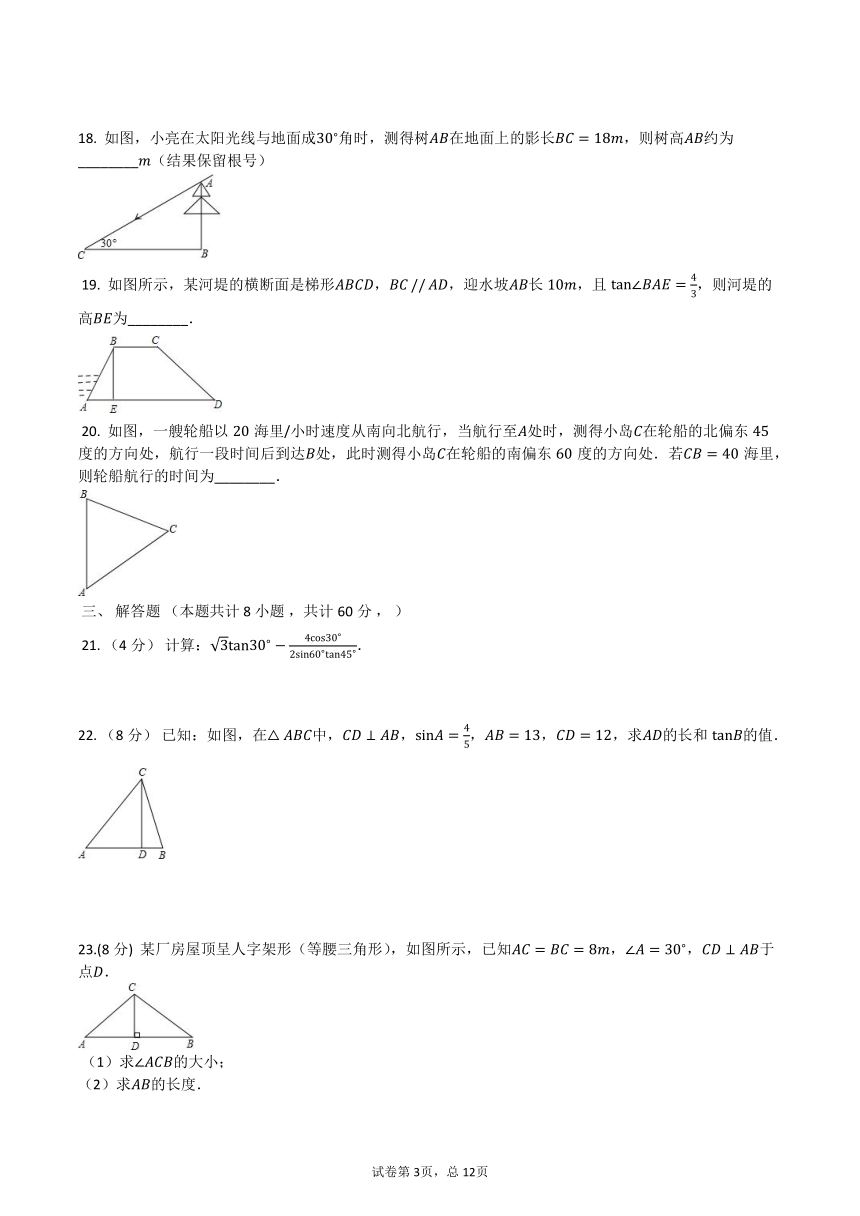
18. 如图,小亮在太阳光线与地面成
30
°
角时,测得树????在地面上的影长????=18??,则树高????约为________??(结果保留根号)
/
?19. 如图所示,某河堤的横断面是梯形????????,?????//?????,迎水坡????长10??,且tan∠??????=
4
3
,则河堤的高????为________.
/
?20. 如图,一艘轮船以20海里/小时速度从南向北航行,当航行至??处时,测得小岛??在轮船的北偏东45度的方向处,航行一段时间后到达??处,此时测得小岛??在轮船的南偏东60度的方向处.若????=40海里,则轮船航行的时间为________.
/
三、 解答题 (本题共计 8 小题 ,共计60分 , )
?21. (4分) 计算:
3
tan
30
°
?
4cos
30
°
2sin
60
°
tan
45
°
.
?
22. (8分) 已知:如图,在△??????中,????⊥????,sin??=
4
5
,????=13,????=12,求????的长和tan??的值.
/
?
23.(8分) 某厂房屋顶呈人字架形(等腰三角形),如图所示,已知????=????=8??,∠??=
30
°
,????⊥????于点??.
/
(1)求∠??????的大小;
(2)求????的长度.
?
24. (8分) 如图,有一电线杆????直立于地面,它的影子正好射在地面????段和与地面成
45
°
角的土坡????上,已知∠??????=
60
°
,????=8米,????=2
2
米,求电线杆????的高.(结果保留3个有效数字,
3
≈1.732)
/
?
25. (8分) 轮船沿着正北方向航行,在??处看到某目标岛屿??在北偏西
30
°
方向,继续向南航行40海里到??处测得这个岛屿方向变成了北偏西
45
°
,若轮船保持航行的方向,则它与目标岛屿最近距离是多少?(结果精确到1海里,参考数据:
2
=1.414,
3
=1.732)
/
?
26. (8分) 已知:如图,在山脚的??处测得山顶??的仰角为
53
°
,沿着坡度为
30
°
的斜坡前进400米到??处(即∠??????=
30
°
,????=400米),测得??的仰角为
63
°
,求此山的高度????.(答案保留根号) (参考数据:sin
53
°
≈
4
5
,cos
53
°
≈
3
5
,tan
53
°
≈
4
3
,sin
63
°
≈
12
13
,cos
63
°
≈
5
13
,tan
63
°
≈
12
5
)
/
?
27. (8分) 酷爱写诗的陈老师,某日到南山采风,结束后步行下山回家,发现下山路????为一条坡度为??=5:12的斜坡,在斜坡下端??处有一座塔,陈老师在??处测得塔顶??的俯角为
14
°
,沿斜坡前行65米到达??处,请根据以上条件求塔的高度????.(参考数据:tan
14
°
≈0.25,sin
14
°
≈0.24,cos
14
°
≈0.97)
/
?
28.(8分) 中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为??(0,?0)、??(80,?0)、??(80,?60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为??的圆形区域(只考虑在海平面上的探测).
/
(1)若在三艘海监船组成的△??????区域内没有探测盲点,则雷达的有效探测半径??至少为________海里;
(2)某时刻海面上出现一艘菲律宾海警船??,在海监船??测得点??位于南偏东
60
°
方向上,同时在海监船??测得??位于北偏东
45
°
方向上,海警船??正以每小时20海里的速度向正西方向移动,我海监船??立刻向北偏东
15
°
方向运动进行拦截,问我海监船??至少以多少速度才能在此方向上拦截到菲律宾海警船???
参考答案与试题解析
【期末专题复习】冀教版九年级数学上册_第26章_解直角三角形_单元检测试卷
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【考点】
锐角三角函数的定义
【解析】
根据锐角三角函数的概念:锐角??的各个三角函数值等于直角三角形的边的比值可直接得到答案.
2.
【答案】
A
【考点】
特殊角的三角函数值
【解析】
直接根据特殊角的三角函数值进行计算即可.
3.
【答案】
C
【考点】
锐角三角函数的增减性
【解析】
先根据锐角三角函数的增减性由sin??4.
【答案】
B
【考点】
同角三角函数的关系
【解析】
根据正弦函数是对边比斜边,余弦函数是邻边比斜边,三角形的两边之和大于第三边,可得答案.
5.
【答案】
A
【考点】
解直角三角形
【解析】
根据锐角三角形函数可以求得????、????和????的长,从而可以求得△??????的面积.
6.
【答案】
A
【考点】
锐角三角函数的定义
【解析】
过点??作????⊥??轴于点??,那么在直角△??????中,????=3,????=4,由勾股定理可得????=5,再由余弦函数的定义得出cos??的值.
7.
【答案】
D
【考点】
解直角三角形的应用
【解析】
首先过点??作????⊥????于点??,得出????=????,????=????,sin
45
°
=
????
????
,进而将各边长用????表示得出即可.
8.
【答案】
D
【考点】
解直角三角形的应用-方向角问题
【解析】
首先过??作作????⊥????于??,求得????的长;设台风中心距??点200????处,刚好处在????上的??,??两点则,在直角三角形中,求得????,????的长,已知速度,则可以求得受影响的时间.
9.
【答案】
C
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
首先设出下降的高度,表示出水平宽度,利用勾股定理即可求解.
10.
【答案】
C
【考点】
解直角三角形的应用-仰角俯角问题
【解析】
根据题意求出????的长,根据三角形的外角的性质和等腰三角形的性质求出????的长,根据正弦的定义计算即可.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
1
【考点】
特殊角的三角函数值
【解析】
将特殊角的三角函数值代入求解即可.
12.
【答案】
15
【考点】
解直角三角形的应用-方向角问题
【解析】
过??作????的垂线,交直线????于点??,分别在????△??????与????△??????中用式子表示????,从而求得????的值,即离小岛??最近的距离.
13.
【答案】
2:
5
:3
【考点】
解直角三角形
【解析】
先利用余弦的定义得到cos??=
????
????
=
2
3
,则可设????=2??,????=3??,再利用勾股定理计算出????,然后计算三角形三边的比.
14.
【答案】
4
5
【考点】
锐角三角函数的定义
【解析】
在直角△??????中利用勾股定理求得????的长,然后利用三角函数的定义求解.
15.
【答案】
4
3
【考点】
互余两角三角函数的关系
【解析】
根据所给的角的正弦值可得两条边的比,进而可得第三边长,tan??的值=∠??的对边与邻边之比.
16.
【答案】
69
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
根据坡度??=1:3,可得出tan??=
????
????
=
1
3
,继而代入数据可求出????的长.
17.
【答案】
7.2
【考点】
解直角三角形的应用-仰角俯角问题
【解析】
根据题意分别在两个直角三角形中求得????和????的长后求差即可得到旗杆的高度.
18.
【答案】
6
3
【考点】
解直角三角形的应用
【解析】
利用所给
30
°
角的正切函数求解即可.
19.
【答案】
8
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
根据tan∠??????=
4
3
得出????,????的关系,根据勾股定理表示出????,再根据????=10,从而得出????的长.
20.
【答案】
(1+
3
)小时
【考点】
解直角三角形的应用-方向角问题
【解析】
作????⊥????于点??,根据题意得:∠??=
45
°
,∠??=
60
°
,然后分别在????△??????中和????△??????中,求得????和????,从而求得线段????的长,利用路程除以速度求得航行的时间.
三、 解答题 (本题共计 8 小题 ,共计60分 )
21.
【答案】
解:原式=
3
×
3
3
?
4×
3
2
2×
3
2
×1
=1?2 =?1.
【考点】
特殊角的三角函数值
【解析】
把特殊角的三角函数值代入后进行二次根式的运算即可.
22.
【答案】
解:∵????⊥????, ∴∠??????=
90
°
… ∵sin??=
????
????
=
4
5
∴????=15.… ∴????=9.… ∴????=4.… ∴tan??=
????
????
=3…
【考点】
解直角三角形
锐角三角函数的定义
【解析】
由sin??=
4
5
,????=12,根据三角函数可得????=15,根据勾股定理可得????=9,则????=4,再根据正切的定义求出tan??的值.
23.
【答案】
解:(1)∵????=????,∠??=
30
°
, ∴∠??=∠??=
30
°
.????????????????????
/
∵∠??+∠??+∠??????=
180
°
, ∴∠??????=
180
°
?∠???∠?? =
180
°
?
30
°
?
30
°
=
120
°
.???????????????????????????
(2)∵????=????,????⊥????, ∴????=2????.????????????????????????? 在????△??????中,∠??=
30
°
,????=8, ∴????=?????cos???????????????????????? =8?cos
30
°
=8×
3
2
=4
3
. ∴????=2????=8
3
(??).?????????????
【考点】
解直角三角形的应用
【解析】
(1)根据等腰三角形的性质,可求得∠??的度数,再根据三角形内角和定理求解;
(2)根据等腰三角形的性质,????=2????.在直角△??????中,根据三角函数求得????的长.从而求解.
24.
【答案】
解:延长????交????的延长线于点??,则∠??=
30
°
,
/
∵∠??????=
45
°
,????⊥????,????=2?
2
米, ∴????=????=2, 在直角三角形??????中,????=
????
tan
30
°
=2?
3
米, ∴????=????+????+????=(10+2?
3
)米, 在直角三角形??????中,????=????×tan
30
°
=
10
3
3
+2≈7.77米.
【考点】
解直角三角形的应用
【解析】
构造∠??为直角,∠??为一内角的直角三角形,由????长易得????,????长,在直角三角形??????中利用
30
°
在正切值可求得????的长,那么可求得线段????的长,在直角三角形??????中利用
30
°
的正切值可求得电线杆????的高.
25.
【答案】
它与目标岛屿最近距离约为55海里.
【考点】
解直角三角形的应用-方向角问题
【解析】
过点??作????⊥????延长线于??.则直角△??????和直角△??????有公共边????,在两个直角三角形中,利用三角函数即可用????表示出????与????,根据????=?????????即可列方程,从而求得????的长,即为所求.
26.
【答案】
此山的高度????为(600
3
?250)米.
【考点】
解直角三角形的应用-仰角俯角问题
解直角三角形的应用-坡度坡角问题
【解析】
首先根据题意分析图形;作????⊥????于??,作????⊥????于??,构造两个直角三角形,分别求解可得????与????的值,再利用图形关系,进而可求出答案.
27.
【答案】
解:如图,过点??作????⊥????于点??. ∵????=65米,tan∠??????=
????
????
=
5
12
, ∴????:????:????=5:12:13, ∴????=25米,????=60米, ∴????=????=60米, ∴????=?????tan
14
°
=60×0.25=15(米). ∴????=????=25?15=10(米).
/
【考点】
解直角三角形的应用-仰角俯角问题
解直角三角形的应用-坡度坡角问题
【解析】
如图,过点??作????⊥????于点??.通过坡度的定义求得????:????:????=5:12:13,则易得????=25米,????=60米,所以利用矩形的性质和解直角△??????求得????的长度即可.
28.
【答案】
50.
(2)过点??作????⊥????于点??,设????=??,由题意得:????=????=??, 则tan
60
°
=
????
????
, ∴????=
??
3
, ∴??+
??
3
=60, 解得:??=90?30
3
, 设船和舰在点??处相遇,海监船的速度为??海里/小时,过点??作????⊥????于点??,设????=??,由题意得: ????=
2
??,????=2??, ∴
2
??
20
=
2??
??
, 解得:??=20
2
, 答:我海监船??至少以20
2
海里/小时速度才能在此方向上拦截到菲律宾海警船??.
【考点】
解直角三角形的应用-方向角问题
【解析】
(1)利用点的坐标性质得出????的长,进而利用直角三角形外心的性质得出答案;
(2)利用方向角画出图形,进而利用锐角三角角函数关系得出即可.
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 在????△??????中,如果各边长度都扩大2倍,则锐角??的正弦值和正切值( )
A.都缩小
1
2
B.都扩大2倍
C.都没有变化
D.不能确定
?2. sin
30
°
的值是( )
A.
1
2
B.
2
2
C.
3
2
D.1
?3. 已知??、??都是锐角,且sin??
B.tan??>tan??
C.cos??>cos??
D.??=??
?4. 如果??是锐角,则下列成立的是( )
A.sin??+cos??=1
B.sin??+cos??>1
C.sin??+cos??<1
D.sin??+cos??≤1
?5. 如图,△??????中,????=5,cos??=
2
2
,sin??=
3
5
,则△??????的面积为( )
/
A.
21
2
B.12
C.14
D.21
?6. 如图,??是∠??的边????上一点,且点??的坐标为(3,?4),则cos??=( )
/
A.
3
5
B.
4
5
C.
3
4
D.
4
3
?7. 小明(??)和小丽(??)两人一前一后放风筝,结果风筝在空中??处纠缠在一起(如示意图).若∠??????=
45
°
,小丽、小明之间的距离与小丽已用的放风筝线的长度相等,则∠??的正切值是( )
/
A.2+
3
B.2?
3
C.
2
+1
D.
2
?1
?8. 温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市??的正西方向300千米的??处(如图),以每小时10
7
千米的速度向东偏南
30
°
的????方向移动,并检测到台风中心在移动过程中,温州市??将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市??的时间会持续多长?( )
/
A.5
B.6
C.8
D.10
?
9. 一人乘雪橇沿坡比1:
3
的斜坡笔直滑下,滑下的距离??(??)与时间??(??)间的关系为??=10??+2
??
2
,若滑到坡底的时间为4??,则此人下降的高度为( )
/
A.72??
B.36
3
??
C.36??
D.18
3
??
?10. 如图,为了测得电视塔的高度????,在??处用高为1米的测角仪????,测得电视塔顶端??的仰角为
30
°
,再向电视塔方向前进120米达到??处,又测得电视塔顶端??的仰角为
60
°
,则这个电视塔的高度????(单位:米)为( )
/
A.60
3
B.61
C.60
3
+1
D.121
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?11. 求值:
sin
2
60
°
+
cos
2
60
°
=________.
?12. 如图,一艘轮船由西向东航行,在??处测得北偏东
68.7
°
反向有小岛??,继续前进60海里到达??处,此时测得小岛??在船的北偏东
26.5
°
方向,则船继续向东航行________海里,离小岛最近(精确到0.1海里,参考数据tan
21.3
°
≈0.39,tan
63.5
°
≈2.01).
/
?13. 在△??????中,∠??=
90
°
,cos??=
2
3
,则??﹕??﹕??为________.
?14. 在????△??????中,∠??=
90
°
,????=3,????=4,那么cos??的值是________.
?15. 已知在????△??????中,∠??=
90
°
,sin??=
3
5
,则tan??的值为________. ?
16. 如示意图,若斜坡????的坡度??=1:3,∠??????=
90
°
,????=23米,则????的长为________米.
/?
17. 如图,某建筑物????上有一旗杆????,从与????相距38??的??处观测旗杆顶部??的仰角为
50
°
,观测旗杆底部??的仰角为
45
°
,则旗杆的高度约为________??.(结果精确到0.1??,参考数据:sin
50
°
≈0.77,cos
50
°
≈0.64,tan
50
°
≈1.19)
/
?
18. 如图,小亮在太阳光线与地面成
30
°
角时,测得树????在地面上的影长????=18??,则树高????约为________??(结果保留根号)
/
?19. 如图所示,某河堤的横断面是梯形????????,?????//?????,迎水坡????长10??,且tan∠??????=
4
3
,则河堤的高????为________.
/
?20. 如图,一艘轮船以20海里/小时速度从南向北航行,当航行至??处时,测得小岛??在轮船的北偏东45度的方向处,航行一段时间后到达??处,此时测得小岛??在轮船的南偏东60度的方向处.若????=40海里,则轮船航行的时间为________.
/
三、 解答题 (本题共计 8 小题 ,共计60分 , )
?21. (4分) 计算:
3
tan
30
°
?
4cos
30
°
2sin
60
°
tan
45
°
.
?
22. (8分) 已知:如图,在△??????中,????⊥????,sin??=
4
5
,????=13,????=12,求????的长和tan??的值.
/
?
23.(8分) 某厂房屋顶呈人字架形(等腰三角形),如图所示,已知????=????=8??,∠??=
30
°
,????⊥????于点??.
/
(1)求∠??????的大小;
(2)求????的长度.
?
24. (8分) 如图,有一电线杆????直立于地面,它的影子正好射在地面????段和与地面成
45
°
角的土坡????上,已知∠??????=
60
°
,????=8米,????=2
2
米,求电线杆????的高.(结果保留3个有效数字,
3
≈1.732)
/
?
25. (8分) 轮船沿着正北方向航行,在??处看到某目标岛屿??在北偏西
30
°
方向,继续向南航行40海里到??处测得这个岛屿方向变成了北偏西
45
°
,若轮船保持航行的方向,则它与目标岛屿最近距离是多少?(结果精确到1海里,参考数据:
2
=1.414,
3
=1.732)
/
?
26. (8分) 已知:如图,在山脚的??处测得山顶??的仰角为
53
°
,沿着坡度为
30
°
的斜坡前进400米到??处(即∠??????=
30
°
,????=400米),测得??的仰角为
63
°
,求此山的高度????.(答案保留根号) (参考数据:sin
53
°
≈
4
5
,cos
53
°
≈
3
5
,tan
53
°
≈
4
3
,sin
63
°
≈
12
13
,cos
63
°
≈
5
13
,tan
63
°
≈
12
5
)
/
?
27. (8分) 酷爱写诗的陈老师,某日到南山采风,结束后步行下山回家,发现下山路????为一条坡度为??=5:12的斜坡,在斜坡下端??处有一座塔,陈老师在??处测得塔顶??的俯角为
14
°
,沿斜坡前行65米到达??处,请根据以上条件求塔的高度????.(参考数据:tan
14
°
≈0.25,sin
14
°
≈0.24,cos
14
°
≈0.97)
/
?
28.(8分) 中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为??(0,?0)、??(80,?0)、??(80,?60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为??的圆形区域(只考虑在海平面上的探测).
/
(1)若在三艘海监船组成的△??????区域内没有探测盲点,则雷达的有效探测半径??至少为________海里;
(2)某时刻海面上出现一艘菲律宾海警船??,在海监船??测得点??位于南偏东
60
°
方向上,同时在海监船??测得??位于北偏东
45
°
方向上,海警船??正以每小时20海里的速度向正西方向移动,我海监船??立刻向北偏东
15
°
方向运动进行拦截,问我海监船??至少以多少速度才能在此方向上拦截到菲律宾海警船???
参考答案与试题解析
【期末专题复习】冀教版九年级数学上册_第26章_解直角三角形_单元检测试卷
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【考点】
锐角三角函数的定义
【解析】
根据锐角三角函数的概念:锐角??的各个三角函数值等于直角三角形的边的比值可直接得到答案.
2.
【答案】
A
【考点】
特殊角的三角函数值
【解析】
直接根据特殊角的三角函数值进行计算即可.
3.
【答案】
C
【考点】
锐角三角函数的增减性
【解析】
先根据锐角三角函数的增减性由sin??
【答案】
B
【考点】
同角三角函数的关系
【解析】
根据正弦函数是对边比斜边,余弦函数是邻边比斜边,三角形的两边之和大于第三边,可得答案.
5.
【答案】
A
【考点】
解直角三角形
【解析】
根据锐角三角形函数可以求得????、????和????的长,从而可以求得△??????的面积.
6.
【答案】
A
【考点】
锐角三角函数的定义
【解析】
过点??作????⊥??轴于点??,那么在直角△??????中,????=3,????=4,由勾股定理可得????=5,再由余弦函数的定义得出cos??的值.
7.
【答案】
D
【考点】
解直角三角形的应用
【解析】
首先过点??作????⊥????于点??,得出????=????,????=????,sin
45
°
=
????
????
,进而将各边长用????表示得出即可.
8.
【答案】
D
【考点】
解直角三角形的应用-方向角问题
【解析】
首先过??作作????⊥????于??,求得????的长;设台风中心距??点200????处,刚好处在????上的??,??两点则,在直角三角形中,求得????,????的长,已知速度,则可以求得受影响的时间.
9.
【答案】
C
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
首先设出下降的高度,表示出水平宽度,利用勾股定理即可求解.
10.
【答案】
C
【考点】
解直角三角形的应用-仰角俯角问题
【解析】
根据题意求出????的长,根据三角形的外角的性质和等腰三角形的性质求出????的长,根据正弦的定义计算即可.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
1
【考点】
特殊角的三角函数值
【解析】
将特殊角的三角函数值代入求解即可.
12.
【答案】
15
【考点】
解直角三角形的应用-方向角问题
【解析】
过??作????的垂线,交直线????于点??,分别在????△??????与????△??????中用式子表示????,从而求得????的值,即离小岛??最近的距离.
13.
【答案】
2:
5
:3
【考点】
解直角三角形
【解析】
先利用余弦的定义得到cos??=
????
????
=
2
3
,则可设????=2??,????=3??,再利用勾股定理计算出????,然后计算三角形三边的比.
14.
【答案】
4
5
【考点】
锐角三角函数的定义
【解析】
在直角△??????中利用勾股定理求得????的长,然后利用三角函数的定义求解.
15.
【答案】
4
3
【考点】
互余两角三角函数的关系
【解析】
根据所给的角的正弦值可得两条边的比,进而可得第三边长,tan??的值=∠??的对边与邻边之比.
16.
【答案】
69
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
根据坡度??=1:3,可得出tan??=
????
????
=
1
3
,继而代入数据可求出????的长.
17.
【答案】
7.2
【考点】
解直角三角形的应用-仰角俯角问题
【解析】
根据题意分别在两个直角三角形中求得????和????的长后求差即可得到旗杆的高度.
18.
【答案】
6
3
【考点】
解直角三角形的应用
【解析】
利用所给
30
°
角的正切函数求解即可.
19.
【答案】
8
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
根据tan∠??????=
4
3
得出????,????的关系,根据勾股定理表示出????,再根据????=10,从而得出????的长.
20.
【答案】
(1+
3
)小时
【考点】
解直角三角形的应用-方向角问题
【解析】
作????⊥????于点??,根据题意得:∠??=
45
°
,∠??=
60
°
,然后分别在????△??????中和????△??????中,求得????和????,从而求得线段????的长,利用路程除以速度求得航行的时间.
三、 解答题 (本题共计 8 小题 ,共计60分 )
21.
【答案】
解:原式=
3
×
3
3
?
4×
3
2
2×
3
2
×1
=1?2 =?1.
【考点】
特殊角的三角函数值
【解析】
把特殊角的三角函数值代入后进行二次根式的运算即可.
22.
【答案】
解:∵????⊥????, ∴∠??????=
90
°
… ∵sin??=
????
????
=
4
5
∴????=15.… ∴????=9.… ∴????=4.… ∴tan??=
????
????
=3…
【考点】
解直角三角形
锐角三角函数的定义
【解析】
由sin??=
4
5
,????=12,根据三角函数可得????=15,根据勾股定理可得????=9,则????=4,再根据正切的定义求出tan??的值.
23.
【答案】
解:(1)∵????=????,∠??=
30
°
, ∴∠??=∠??=
30
°
.????????????????????
/
∵∠??+∠??+∠??????=
180
°
, ∴∠??????=
180
°
?∠???∠?? =
180
°
?
30
°
?
30
°
=
120
°
.???????????????????????????
(2)∵????=????,????⊥????, ∴????=2????.????????????????????????? 在????△??????中,∠??=
30
°
,????=8, ∴????=?????cos???????????????????????? =8?cos
30
°
=8×
3
2
=4
3
. ∴????=2????=8
3
(??).?????????????
【考点】
解直角三角形的应用
【解析】
(1)根据等腰三角形的性质,可求得∠??的度数,再根据三角形内角和定理求解;
(2)根据等腰三角形的性质,????=2????.在直角△??????中,根据三角函数求得????的长.从而求解.
24.
【答案】
解:延长????交????的延长线于点??,则∠??=
30
°
,
/
∵∠??????=
45
°
,????⊥????,????=2?
2
米, ∴????=????=2, 在直角三角形??????中,????=
????
tan
30
°
=2?
3
米, ∴????=????+????+????=(10+2?
3
)米, 在直角三角形??????中,????=????×tan
30
°
=
10
3
3
+2≈7.77米.
【考点】
解直角三角形的应用
【解析】
构造∠??为直角,∠??为一内角的直角三角形,由????长易得????,????长,在直角三角形??????中利用
30
°
在正切值可求得????的长,那么可求得线段????的长,在直角三角形??????中利用
30
°
的正切值可求得电线杆????的高.
25.
【答案】
它与目标岛屿最近距离约为55海里.
【考点】
解直角三角形的应用-方向角问题
【解析】
过点??作????⊥????延长线于??.则直角△??????和直角△??????有公共边????,在两个直角三角形中,利用三角函数即可用????表示出????与????,根据????=?????????即可列方程,从而求得????的长,即为所求.
26.
【答案】
此山的高度????为(600
3
?250)米.
【考点】
解直角三角形的应用-仰角俯角问题
解直角三角形的应用-坡度坡角问题
【解析】
首先根据题意分析图形;作????⊥????于??,作????⊥????于??,构造两个直角三角形,分别求解可得????与????的值,再利用图形关系,进而可求出答案.
27.
【答案】
解:如图,过点??作????⊥????于点??. ∵????=65米,tan∠??????=
????
????
=
5
12
, ∴????:????:????=5:12:13, ∴????=25米,????=60米, ∴????=????=60米, ∴????=?????tan
14
°
=60×0.25=15(米). ∴????=????=25?15=10(米).
/
【考点】
解直角三角形的应用-仰角俯角问题
解直角三角形的应用-坡度坡角问题
【解析】
如图,过点??作????⊥????于点??.通过坡度的定义求得????:????:????=5:12:13,则易得????=25米,????=60米,所以利用矩形的性质和解直角△??????求得????的长度即可.
28.
【答案】
50.
(2)过点??作????⊥????于点??,设????=??,由题意得:????=????=??, 则tan
60
°
=
????
????
, ∴????=
??
3
, ∴??+
??
3
=60, 解得:??=90?30
3
, 设船和舰在点??处相遇,海监船的速度为??海里/小时,过点??作????⊥????于点??,设????=??,由题意得: ????=
2
??,????=2??, ∴
2
??
20
=
2??
??
, 解得:??=20
2
, 答:我海监船??至少以20
2
海里/小时速度才能在此方向上拦截到菲律宾海警船??.
【考点】
解直角三角形的应用-方向角问题
【解析】
(1)利用点的坐标性质得出????的长,进而利用直角三角形外心的性质得出答案;
(2)利用方向角画出图形,进而利用锐角三角角函数关系得出即可.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
