湘教版九年级下《第一章二次函数》单元试卷(含答案)
文档属性
| 名称 | 湘教版九年级下《第一章二次函数》单元试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-26 19:16:15 | ||
图片预览

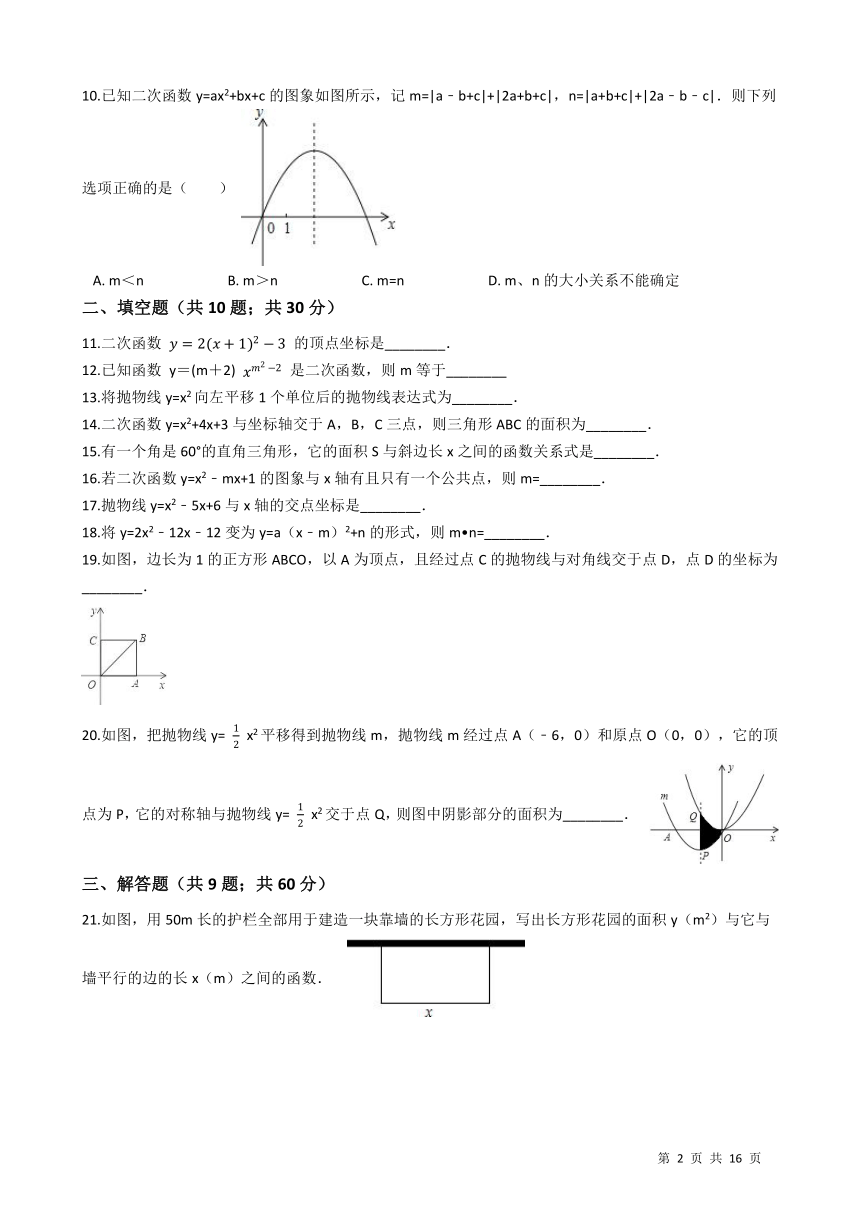
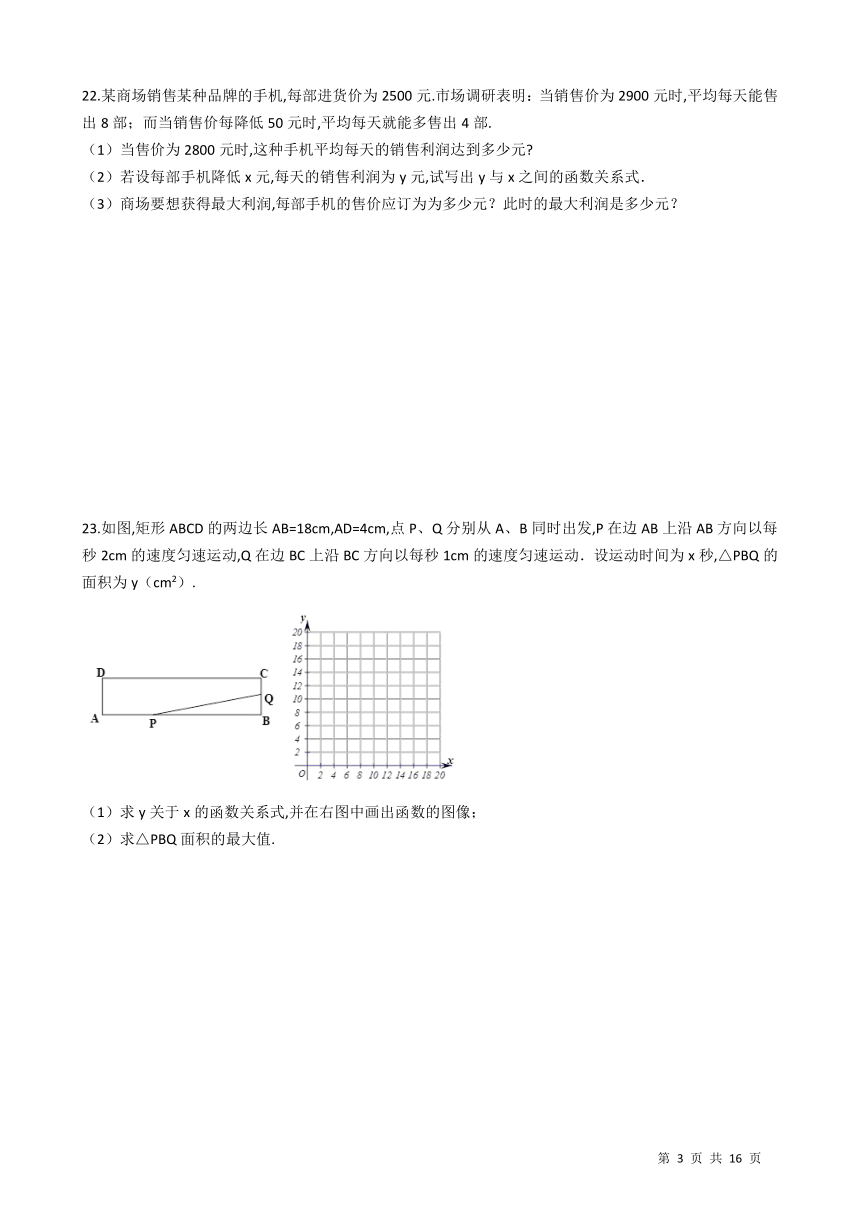


文档简介
【期末专题复习】湘教版九年级数学下册 第一章 二次函数 单元检测试卷
一、单选题(共10题;共30分)
1.下列函数是二次函数的是(? )
A.?y=
1
??
?????????????????????????????/B.?y=2x-3?????????????????????????????/C.?y=3x2+
1
??
2
?????????????????????????????/D.?y=8x2+1
2.已知二次函数y=(x+1)2+(x﹣3)2 , 当函数y取最小值时,x的值是(?? )
A.?x=﹣1????????????????????????????????????/B.?x=3????????????????????????????????????/C.?x=2????????????????????????????????????/D.?x=1
3.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4
0
﹣2
﹣2
0
4
…
下列说法正确的是(?? )
A.?抛物线的开口向下??????????????????????????????????????????????/B.?当x>﹣3时,y随x的增大而增大 C.?二次函数的最小值是﹣2?????????????????????????????????????/D.?抛物线的对称轴是x=﹣
5
2
4.下列抛物线中,与/轴有两个交点的是(?????????)
A.?y=5x2-7x+5????????????????/B.?y=16x2-24x+9????????????????/C.?y=2x2+3x-4????????????????/D.?y=3x2-2
6
x+2
5.y=x2+(1-a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是(?)
A.?a=5?????????????????????????????????????/B.?a≥5?????????????????????????????????????/C.?a=3?????????????????????????????????????/D.?a≥3
6.将抛物线y=x2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为(?? )
A.?y=(x﹣1)2+2????????????/B.?y=(x+1)2+2??????????????/C.?y=(x﹣1)2﹣2????????????/D.?y=(x+1)2﹣2
7.二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论正确的是( ) /
A.?abc>0???????????????????????????????????????????????????????????????/B.?方程ax2+bx+c=0有两个实数根分别为-2和6 C.?a-b+c<0???????????????????????????????????????????????????????????/D.?当y=4时,x的取值只能为0
8.二次函数y=﹣(x﹣1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为(?? )
A.?
5
2
??????????????????????????????????????????/B.?2??????????????????????????????????????????/C.?
3
2
??????????????????????????????????????????/D.?
1
2
9.把抛物线y=ax2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x2-2x+3,则b+c的值为(????)
A.?9?????????????????????????????????????????/B.?12?????????????????????????????????????????/C.?-14?????????????????????????????????????????/D.?10
10.已知二次函数y=ax2+bx+c的图象如图所示,记m=|a﹣b+c|+|2a+b+c|,n=|a+b+c|+|2a﹣b﹣c|.则下列选项正确的是( ) /
A.?m<n????????????????????????/B.?m>n????????????????????????/C.?m=n????????????????????????/D.?m、n的大小关系不能确定
二、填空题(共10题;共30分)
11.二次函数 ??=2
(??+1)
2
?3 的顶点坐标是________.
12.已知函数 y=(m+2)
??
??
2
?2
是二次函数,则m等于________
13.将抛物线y=x2向左平移1个单位后的抛物线表达式为________.
14.二次函数y=x2+4x+3与坐标轴交于A,B,C三点,则三角形ABC的面积为________.
15.有一个角是60°的直角三角形,它的面积S与斜边长x之间的函数关系式是________.
16.若二次函数y=x2﹣mx+1的图象与x轴有且只有一个公共点,则m=________.
17.抛物线y=x2﹣5x+6与x轴的交点坐标是________.
18.将y=2x2﹣12x﹣12变为y=a(x﹣m)2+n的形式,则m?n=________.
19.如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,点D的坐标为________. /
20.如图,把抛物线y=
1
2
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
1
2
x2交于点Q,则图中阴影部分的面积为________. /
三、解答题(共9题;共60分)
21.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数. /
22.某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部. (1)当售价为2800元时,这种手机平均每天的销售利润达到多少元? (2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式. (3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
23.如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2). // (1)求y关于x的函数关系式,并在右图中画出函数的图像; (2)求△PBQ面积的最大值.
24.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴. / (1)求该抛物线的解析式. (2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式. (3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
25.已知二次函数y=-
1
4
??
2
+
3
2
??的图象如图. (1)求它的对称轴与x轴交点D的坐标; (2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式; (3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由. /
26.如图,梯形ABCD中,AB∥CD,AB=14,AD= 4
2
, CD=7.直线l经过A,D两点,且sin∠DAB=
2
2
. 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S. / (1)求腰BC的长; (2)当Q在BC上运动时,求S与t的函数关系式; (3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的
1
4
?若存在,请求出t的值;若不存在,请说明理由; (4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
27.已知直线l:y=kx和抛物线C:y=ax2+bx+1. (Ⅰ)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值; (Ⅱ)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点; (i)求此抛物线的解析式; (ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,求证:OP=PQ.
28.(2017·金华)(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 y=a(x-4
)
2
+h ,已知点O与球网的水平距离为5m,球网的高度1.55m. /
(1)当a=?
1
24
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为
12
5
m的Q处时,乙扣球成功,求a的值.
29.?已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm. 如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5). / 解答下列问题: (1)当t为何值时,点A在线段PQ的垂直平分线上? (2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由. (3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
答案解析部分
一、单选题
1.【答案】D
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】A
二、填空题
11.【答案】(?1,??3)
12.【答案】2
13.【答案】y=(x+1)2
14.【答案】3
15.【答案】
3
8
x2
16.【答案】±2
17.【答案】(3,0),(2,0)
18.【答案】﹣90
19.【答案】(
3?
5
2
,
3?
5
2
)
20.【答案】
27
2
三、解答题
21.【答案】解:∵与墙平行的边的长为x(m),则垂直于墙的边长为: /?=(25﹣0.5x)m, 根据题意得出:y=x(25﹣0.5x)=﹣0.5x2+25x
22.【答案】解:(1)当售价为2800元时,销售价降低100元,平均每天就能售出16部. 所以:这种手机平均每天的销售利润为:16×(2800-2500)=4800(元); (2)根据题意,得y=(2900-2500-x)(8+4×
??
50
), 即y=?
2
25
x2+24x+3200; (3)对于y=?
2
25
x2+24x+3200, 当x=?
24
2×
?
2
25
=150时, y最大值=(2900-2500-150)(8+4×
150
50
)=5000(元) 2900-150=2750(元) 所以,每台手机降价2750元时,商场每天销售这种手机的利润最大,最大利润是5000元.
23.【答案】(1)∵S△PBQ=/?PB·BQ,? PB=AB-AP=18-2x,BQ=x, ∴y=/(18-2x)x, 即y=-x2+9x(024.【答案】解:(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),
∴假设二次函数解析式为:y=a(x-1)(x-3),
将D(0,3),代入y=a(x-1)(x-3),
得:3=3a,∴a=1,
∴抛物线的解析式为:y=a(x-1)(x-3)=x2-4x+3;
(2)∵过点A(-1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,
∴
1
2
AC×BC=6, ∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点, ∴二次函数对称轴为x=2, ∴AC=3, ∴BC=4, ∴B点坐标为:(2,4)或(2,-4), 一次函数解析式为;y=kx+b,当点B为(2,4)时, ∴
4=2??+??
0=???+??
,解得:
??=
4
3
??=
4
3
, ∴y=
4
3
x+
4
3
; 当点B为(2,-4)时,
?4=2??+??
0=???+??
,解得
??=?
4
3
??=?
4
3
, ∴y=?
4
3
x?
4
3
, ∴直线AB的解析式为:y=
4
3
x+
4
3
或y=?
4
3
x?
4
3
; (3)∵当点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切, 设⊙P与AB相切于点Q,与x轴相切于点C; ∴PQ⊥AB,AQ=AC,PQ=PC, ∵AC=1+2=3,BC=4, ∴AB=5,AQ=3, ∴BQ=2, ∵∠QBP=∠ABC, ∠BQP=∠ACB, ∴△ABC∽△PBQ, ∴
????
????
=
????
????
=
????
????
, ∴
2
4
=
????
3
, ∴PC=1.5, P点坐标为:(2,1.5), 同理可得(2,-1.5),(2,-6),(2,6).
25.【答案】解:(1)由y=-
1
4
??
2
+
3
2
??, 得x=﹣
??
2??
=﹣
3
2
2×
?
1
4
=3, ∴D(3,0); (2)方法一: / 如图1,设平移后的抛物线的解析式为y=-
1
4
??
2
+
3
2
??+k, 则C(0,k)OC=k, 令y=0即-
1
4
??
2
+
3
2
??+k=0, 得3+
4??+9
,x2=3﹣
4??+9
, ∴A(3-
4??+9
,0),B(3+
4??+9
,0) ∴AB2=(
4??+9
+3-3+
4??+9
)2=16k+36 AC2+BC2=(3-
4??+9
)2+k2+(3+
4??+9
)2=2k2+8k+36, ∵AC2+BC2=AB2 即:2k2+8k+36=16k+36, 得k1=4,k2=0(舍去), ∴抛物线的解析式为-
1
4
??
2
+
3
2
??+4, 方法二: ∵y=-
1
4
??
2
+
3
2
??,∴顶点坐标(3,
9
4
), 设抛物线向上平移h个单位,则得到C(0,h),顶点坐标M(3,
9
4
+h) ∴平移后的抛物线:y=-
1
4
???3
2
+
9
4
+h, 当y=0时,-
1
4
???3
2
+
9
4
+h,,得x1=3-
4?+9
,x2=3+
4?+9
, ∴A(3-
4?+9
,0),B(3+
4?+9
,0) ∵∠ACB=90°, ∴△AOC∽△COB,则OC2=OA?OB, 即h2=(
4?+9
-3)(
4?+9
+3) 解得h1=4,h2=0(不合题意舍去), ∴平移后的抛物线:y=-
1
4
???3
2
+
9
4
+4=-
1
4
???3
2
+
25
4
(3)方法一: / 如图2,由抛物线的解析式y=-
1
4
??
2
+
3
2
??+4可得, A(﹣2,0),B(8,0),C(0,4),M(3,
25
4
), 过C、M作直线,连接CD,过M作MH垂直y轴于H,则MH=3, ∴??
??
2
=
25
4
2
=
625
16
, ??
??
2
=??
??
2
+??
??
2
=
3
2
+
25
4
?4
2
=
225
16
, 在Rt△COD中,CD=
3
2
+
4
2
=5=AD, ∴点C在⊙D上, ∵??
??
2
=
25
4
2
=
625
16
??
??
2
+??
??
2
=
5
2
+
225
16
=
25
4
2
=
625
16
, ∴DM2=CM2+CD2 ∴△CDM是直角三角形,∴CD⊥CM, ∴直线CM与⊙D相切. 方法二: / 如图3,由抛物线的解析式可得A(﹣2,0),B(8,0),C(0,4),M(3,
25
4
), 作直线CM,过D作DE⊥CM于E,过M作MH垂直y轴于H,则MH=3,DM=
25
4
,由勾股定理得CM=
15
4
, ∵DM∥OC, ∴∠MCH=∠EMD, ∴Rt△CMH∽Rt△DME, ∴
????
????
=
????
????
得DE=5, 由(2)知AB=10,∴⊙D的半径为5. ∴直线CM与⊙D相切.
26.【答案】解:(1)5? (2) 在点P、Q运动的过程中: ①当0<t≤1时,过点Q作QE⊥AB轴于点E,如图1: 则BE=BQ?cos∠CBF=5t?
3
5
=3t. ∴PE=PB﹣BE=(14﹣2t)﹣3t=14﹣5t, S=
1
2
PM?PE=
1
2
×2t×(14﹣5t)=﹣5t2+14t; ②当1<t≤2时,如图2: / 过点C、Q分别作x轴的垂线,垂足分别为F,E, 则CQ=5t﹣5,PE=AF﹣AP﹣EF=11﹣2t﹣(5t﹣5)=16﹣7t, S=
1
2
PM?PE=
1
2
×2t×(16﹣7t)=﹣7t2+16t; ③当点M与点Q相遇时,DM+CQ=CD=7, 即(2t﹣4)+(5t﹣5)=7,解得t=
16
7
. 当2<t<
16
7
时,如图3: / MQ=CD﹣DM﹣CQ=7﹣(2t﹣4)﹣(5t﹣5)=16﹣7t, S=
1
2
PM?MQ=
1
2
×4×(16﹣7t)=﹣14t+32. (3)梯形ABCD的面积为42 ﹣5t2+14t=
1
4
×42,方程无解,所以△MPQ的面积不能为梯形ABCD的
1
4
。 (4)△QMN为等腰三角形,有两种情形: ①如图4所示,点M在线段NM的右侧上 /, MQ=CD-DM-CQ=7-(2t-4)-(5t-5)=16-7t,MN=DM=2t-4, 由MN=MQ,得16-7t=2t-4,解得:t=
20
9
; ②如图5所示,当Q在MN的左侧时,5t-5+(2t-4)-7=(2t-4)+4-4, / 解得:t=
12
5
. 故当t=
20
9
或t=
12
5
时,△QMN为等腰三角形.
27.【答案】解:(Ⅰ)将k=1,b=1代入代入得:抛物线的解析式为y=ax2+x+1,直线的解析式为y=x. ∵y=ax2+x+1=a(x+
1
2??
)2+1﹣
1
4??
, ∴抛物线的顶点为(﹣
1
2??
,1﹣
1
4??
). ∵抛物线的顶点在直线y=x上, ∴﹣
1
2??
=1﹣
1
4??
,解得:a=﹣
1
4
. (Ⅱ)(i)将直线y=kx向上平移k2+1个单位,所得直线的解析式为y=kx+k2+1. ∵无论非零实数k取何值,直线与抛物线都只有一个交点, ∴方程kx+k2+1=ax2+bx+1有两个相等的实数根,即ax2+(b﹣k)x﹣k2=0有两个相等的实数根, ∴△=(b﹣k)2+4ak2=(4a+1)k2﹣2bk+b2=0. ∵无论非零实数k取何值时,(4a+1)k2﹣2bk+b2=0恒成立, ∴4a+1=0且b=0, ∴a=﹣
1
4
,b=0. ∴抛物线的解析式为y=﹣
1
4
x2+1. (ii)证明:根据题意,画出图象如图所示: / 设点P的坐标为(x,﹣
1
4
x2+1)则点Q的坐标为(x,2),D(x,0). ∴PD=|﹣
1
4
x2+1|,OD=|x|,QP=2﹣(﹣
1
4
x2+1)=
1
4
x2+1. 在Rt△OPD中,依据勾股定理得:OP=
??
2
+
(?
1
4
??
2
+1)
2
=
1
16
??
4
+
1
2
??
2
+1
=
1
4
x2+1. ∴OP=PQ
28.【答案】(1)解:①∵a=?
1
24
,P(0,1); ∴1=?
1
24
0?4
2
+h; ∴h=
5
3
; ②把x=5代入y=?
1
24
???4
2
+
5
3
得: y=?
1
24
5?4
2
+
5
3
=1.625; ∵1.625>1.55; ∴此球能过网. (2)解:把(0,1),(7,
12
5
)代入y=a
???4
2
+?得:;
16??+?=1
9??+?=
12
5
;解得:
??=?
1
5
?=
21
5
; ∴a=?
1
5
.
29.【答案】解:(1)∵点A在线段PQ的垂直平分线上, ∴AP = AQ. ∵∠DEF = 45°,∠ACB = 90°,∠DEF+∠ACB+∠EQC = 180°, ∴∠EQC = 45°. ∴∠DEF =∠EQC. ∴CE =" CQ." 由题意知:CE = t,BP ="2" t,?????????? ∴CQ = t. ∴AQ = 8-t. 在Rt△ABC中,由勾股定理得:AB =" 10" cm . 则AP = 10-2 t. ∴10-2 t = 8-t. 解得:t = 2. 答:当t =" 2" s时,点A在线段PQ的垂直平分线上.??????4分 (2)过P作????⊥????,交BE于M,∴∠??????=90°. / 在Rt△ABC和Rt△BPM中,sin??=
????
????
=
????
????
, ∴
????
2??
=
8
10
.??∴PM = ????=
8
5
??. ∵BC =" 6" cm,CE = t,?∴BE = 6-t. ∴y = S△ABC-S△BPE =
1
2
????·?????
1
2
????·????=
1
2
×6×8?
1
2
×
6???
×
8
5
?? =
4
5
??
2
?
24
5
??+24 =
4
5
(???3
)
2
+
84
5
. ∵??=
4
5
>0,∴抛物线开口向上. ∴当t = 3时,y最小=/. 答:当t = 3s时,四边形APEC的面积最小,最小面积为
84
5
cm2.?? 8分 (3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上. / 过P作????⊥????,交AC于N, ∴∠??????=∠??????=∠??????=90°. ∵∠??????=∠??????,∴△PAN ∽△BAC. ∴
????
????
=
????
????
=
????
????
. ∴
????
6
=
10?2??
10
=
????
8
. ∴????=6?
6
5
??,????=8?
8
5
??. ∵NQ = AQ-AN, ∴NQ = 8-t-(8?
8
5
??)=
3
5
??. ∵∠ACB = 90°,B、C(E)、F在同一条直线上, ∴∠QCF = 90°,∠QCF = ∠PNQ. ∵∠FQC = ∠PQN, ∴△QCF∽△QNP . ∴
????
????
=
????
????
.?∴
6?
6
5
??
9???
=
3
5
??
??
.? ∵06?
6
5
??
9???
=
3
5
解得:t = 1. 答:当t = 1s,点P、Q、F三点在同一条直线上.?
一、单选题(共10题;共30分)
1.下列函数是二次函数的是(? )
A.?y=
1
??
?????????????????????????????/B.?y=2x-3?????????????????????????????/C.?y=3x2+
1
??
2
?????????????????????????????/D.?y=8x2+1
2.已知二次函数y=(x+1)2+(x﹣3)2 , 当函数y取最小值时,x的值是(?? )
A.?x=﹣1????????????????????????????????????/B.?x=3????????????????????????????????????/C.?x=2????????????????????????????????????/D.?x=1
3.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4
0
﹣2
﹣2
0
4
…
下列说法正确的是(?? )
A.?抛物线的开口向下??????????????????????????????????????????????/B.?当x>﹣3时,y随x的增大而增大 C.?二次函数的最小值是﹣2?????????????????????????????????????/D.?抛物线的对称轴是x=﹣
5
2
4.下列抛物线中,与/轴有两个交点的是(?????????)
A.?y=5x2-7x+5????????????????/B.?y=16x2-24x+9????????????????/C.?y=2x2+3x-4????????????????/D.?y=3x2-2
6
x+2
5.y=x2+(1-a)x+1是关于x的二次函数,当x的取值范围是1≤x≤3时,y在x=1时取得最大值,则实数a的取值范围是(?)
A.?a=5?????????????????????????????????????/B.?a≥5?????????????????????????????????????/C.?a=3?????????????????????????????????????/D.?a≥3
6.将抛物线y=x2向右平移1个单位长度,再向上平移2个单位长度所得的抛物线解析式为(?? )
A.?y=(x﹣1)2+2????????????/B.?y=(x+1)2+2??????????????/C.?y=(x﹣1)2﹣2????????????/D.?y=(x+1)2﹣2
7.二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论正确的是( ) /
A.?abc>0???????????????????????????????????????????????????????????????/B.?方程ax2+bx+c=0有两个实数根分别为-2和6 C.?a-b+c<0???????????????????????????????????????????????????????????/D.?当y=4时,x的取值只能为0
8.二次函数y=﹣(x﹣1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为(?? )
A.?
5
2
??????????????????????????????????????????/B.?2??????????????????????????????????????????/C.?
3
2
??????????????????????????????????????????/D.?
1
2
9.把抛物线y=ax2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y=x2-2x+3,则b+c的值为(????)
A.?9?????????????????????????????????????????/B.?12?????????????????????????????????????????/C.?-14?????????????????????????????????????????/D.?10
10.已知二次函数y=ax2+bx+c的图象如图所示,记m=|a﹣b+c|+|2a+b+c|,n=|a+b+c|+|2a﹣b﹣c|.则下列选项正确的是( ) /
A.?m<n????????????????????????/B.?m>n????????????????????????/C.?m=n????????????????????????/D.?m、n的大小关系不能确定
二、填空题(共10题;共30分)
11.二次函数 ??=2
(??+1)
2
?3 的顶点坐标是________.
12.已知函数 y=(m+2)
??
??
2
?2
是二次函数,则m等于________
13.将抛物线y=x2向左平移1个单位后的抛物线表达式为________.
14.二次函数y=x2+4x+3与坐标轴交于A,B,C三点,则三角形ABC的面积为________.
15.有一个角是60°的直角三角形,它的面积S与斜边长x之间的函数关系式是________.
16.若二次函数y=x2﹣mx+1的图象与x轴有且只有一个公共点,则m=________.
17.抛物线y=x2﹣5x+6与x轴的交点坐标是________.
18.将y=2x2﹣12x﹣12变为y=a(x﹣m)2+n的形式,则m?n=________.
19.如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,点D的坐标为________. /
20.如图,把抛物线y=
1
2
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
1
2
x2交于点Q,则图中阴影部分的面积为________. /
三、解答题(共9题;共60分)
21.如图,用50m长的护栏全部用于建造一块靠墙的长方形花园,写出长方形花园的面积y(m2)与它与墙平行的边的长x(m)之间的函数. /
22.某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部. (1)当售价为2800元时,这种手机平均每天的销售利润达到多少元? (2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式. (3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
23.如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2). // (1)求y关于x的函数关系式,并在右图中画出函数的图像; (2)求△PBQ面积的最大值.
24.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴. / (1)求该抛物线的解析式. (2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式. (3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
25.已知二次函数y=-
1
4
??
2
+
3
2
??的图象如图. (1)求它的对称轴与x轴交点D的坐标; (2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与x轴,y轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式; (3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由. /
26.如图,梯形ABCD中,AB∥CD,AB=14,AD= 4
2
, CD=7.直线l经过A,D两点,且sin∠DAB=
2
2
. 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S. / (1)求腰BC的长; (2)当Q在BC上运动时,求S与t的函数关系式; (3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的
1
4
?若存在,请求出t的值;若不存在,请说明理由; (4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
27.已知直线l:y=kx和抛物线C:y=ax2+bx+1. (Ⅰ)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值; (Ⅱ)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点; (i)求此抛物线的解析式; (ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,求证:OP=PQ.
28.(2017·金华)(本题8分) 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲 在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 y=a(x-4
)
2
+h ,已知点O与球网的水平距离为5m,球网的高度1.55m. /
(1)当a=?
1
24
时,①求h的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为
12
5
m的Q处时,乙扣球成功,求a的值.
29.?已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm. 如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5). / 解答下列问题: (1)当t为何值时,点A在线段PQ的垂直平分线上? (2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由. (3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
答案解析部分
一、单选题
1.【答案】D
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】A
二、填空题
11.【答案】(?1,??3)
12.【答案】2
13.【答案】y=(x+1)2
14.【答案】3
15.【答案】
3
8
x2
16.【答案】±2
17.【答案】(3,0),(2,0)
18.【答案】﹣90
19.【答案】(
3?
5
2
,
3?
5
2
)
20.【答案】
27
2
三、解答题
21.【答案】解:∵与墙平行的边的长为x(m),则垂直于墙的边长为: /?=(25﹣0.5x)m, 根据题意得出:y=x(25﹣0.5x)=﹣0.5x2+25x
22.【答案】解:(1)当售价为2800元时,销售价降低100元,平均每天就能售出16部. 所以:这种手机平均每天的销售利润为:16×(2800-2500)=4800(元); (2)根据题意,得y=(2900-2500-x)(8+4×
??
50
), 即y=?
2
25
x2+24x+3200; (3)对于y=?
2
25
x2+24x+3200, 当x=?
24
2×
?
2
25
=150时, y最大值=(2900-2500-150)(8+4×
150
50
)=5000(元) 2900-150=2750(元) 所以,每台手机降价2750元时,商场每天销售这种手机的利润最大,最大利润是5000元.
23.【答案】(1)∵S△PBQ=/?PB·BQ,? PB=AB-AP=18-2x,BQ=x, ∴y=/(18-2x)x, 即y=-x2+9x(0
1
2
AC×BC=6, ∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点, ∴二次函数对称轴为x=2, ∴AC=3, ∴BC=4, ∴B点坐标为:(2,4)或(2,-4), 一次函数解析式为;y=kx+b,当点B为(2,4)时, ∴
4=2??+??
0=???+??
,解得:
??=
4
3
??=
4
3
, ∴y=
4
3
x+
4
3
; 当点B为(2,-4)时,
?4=2??+??
0=???+??
,解得
??=?
4
3
??=?
4
3
, ∴y=?
4
3
x?
4
3
, ∴直线AB的解析式为:y=
4
3
x+
4
3
或y=?
4
3
x?
4
3
; (3)∵当点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切, 设⊙P与AB相切于点Q,与x轴相切于点C; ∴PQ⊥AB,AQ=AC,PQ=PC, ∵AC=1+2=3,BC=4, ∴AB=5,AQ=3, ∴BQ=2, ∵∠QBP=∠ABC, ∠BQP=∠ACB, ∴△ABC∽△PBQ, ∴
????
????
=
????
????
=
????
????
, ∴
2
4
=
????
3
, ∴PC=1.5, P点坐标为:(2,1.5), 同理可得(2,-1.5),(2,-6),(2,6).
25.【答案】解:(1)由y=-
1
4
??
2
+
3
2
??, 得x=﹣
??
2??
=﹣
3
2
2×
?
1
4
=3, ∴D(3,0); (2)方法一: / 如图1,设平移后的抛物线的解析式为y=-
1
4
??
2
+
3
2
??+k, 则C(0,k)OC=k, 令y=0即-
1
4
??
2
+
3
2
??+k=0, 得3+
4??+9
,x2=3﹣
4??+9
, ∴A(3-
4??+9
,0),B(3+
4??+9
,0) ∴AB2=(
4??+9
+3-3+
4??+9
)2=16k+36 AC2+BC2=(3-
4??+9
)2+k2+(3+
4??+9
)2=2k2+8k+36, ∵AC2+BC2=AB2 即:2k2+8k+36=16k+36, 得k1=4,k2=0(舍去), ∴抛物线的解析式为-
1
4
??
2
+
3
2
??+4, 方法二: ∵y=-
1
4
??
2
+
3
2
??,∴顶点坐标(3,
9
4
), 设抛物线向上平移h个单位,则得到C(0,h),顶点坐标M(3,
9
4
+h) ∴平移后的抛物线:y=-
1
4
???3
2
+
9
4
+h, 当y=0时,-
1
4
???3
2
+
9
4
+h,,得x1=3-
4?+9
,x2=3+
4?+9
, ∴A(3-
4?+9
,0),B(3+
4?+9
,0) ∵∠ACB=90°, ∴△AOC∽△COB,则OC2=OA?OB, 即h2=(
4?+9
-3)(
4?+9
+3) 解得h1=4,h2=0(不合题意舍去), ∴平移后的抛物线:y=-
1
4
???3
2
+
9
4
+4=-
1
4
???3
2
+
25
4
(3)方法一: / 如图2,由抛物线的解析式y=-
1
4
??
2
+
3
2
??+4可得, A(﹣2,0),B(8,0),C(0,4),M(3,
25
4
), 过C、M作直线,连接CD,过M作MH垂直y轴于H,则MH=3, ∴??
??
2
=
25
4
2
=
625
16
, ??
??
2
=??
??
2
+??
??
2
=
3
2
+
25
4
?4
2
=
225
16
, 在Rt△COD中,CD=
3
2
+
4
2
=5=AD, ∴点C在⊙D上, ∵??
??
2
=
25
4
2
=
625
16
??
??
2
+??
??
2
=
5
2
+
225
16
=
25
4
2
=
625
16
, ∴DM2=CM2+CD2 ∴△CDM是直角三角形,∴CD⊥CM, ∴直线CM与⊙D相切. 方法二: / 如图3,由抛物线的解析式可得A(﹣2,0),B(8,0),C(0,4),M(3,
25
4
), 作直线CM,过D作DE⊥CM于E,过M作MH垂直y轴于H,则MH=3,DM=
25
4
,由勾股定理得CM=
15
4
, ∵DM∥OC, ∴∠MCH=∠EMD, ∴Rt△CMH∽Rt△DME, ∴
????
????
=
????
????
得DE=5, 由(2)知AB=10,∴⊙D的半径为5. ∴直线CM与⊙D相切.
26.【答案】解:(1)5? (2) 在点P、Q运动的过程中: ①当0<t≤1时,过点Q作QE⊥AB轴于点E,如图1: 则BE=BQ?cos∠CBF=5t?
3
5
=3t. ∴PE=PB﹣BE=(14﹣2t)﹣3t=14﹣5t, S=
1
2
PM?PE=
1
2
×2t×(14﹣5t)=﹣5t2+14t; ②当1<t≤2时,如图2: / 过点C、Q分别作x轴的垂线,垂足分别为F,E, 则CQ=5t﹣5,PE=AF﹣AP﹣EF=11﹣2t﹣(5t﹣5)=16﹣7t, S=
1
2
PM?PE=
1
2
×2t×(16﹣7t)=﹣7t2+16t; ③当点M与点Q相遇时,DM+CQ=CD=7, 即(2t﹣4)+(5t﹣5)=7,解得t=
16
7
. 当2<t<
16
7
时,如图3: / MQ=CD﹣DM﹣CQ=7﹣(2t﹣4)﹣(5t﹣5)=16﹣7t, S=
1
2
PM?MQ=
1
2
×4×(16﹣7t)=﹣14t+32. (3)梯形ABCD的面积为42 ﹣5t2+14t=
1
4
×42,方程无解,所以△MPQ的面积不能为梯形ABCD的
1
4
。 (4)△QMN为等腰三角形,有两种情形: ①如图4所示,点M在线段NM的右侧上 /, MQ=CD-DM-CQ=7-(2t-4)-(5t-5)=16-7t,MN=DM=2t-4, 由MN=MQ,得16-7t=2t-4,解得:t=
20
9
; ②如图5所示,当Q在MN的左侧时,5t-5+(2t-4)-7=(2t-4)+4-4, / 解得:t=
12
5
. 故当t=
20
9
或t=
12
5
时,△QMN为等腰三角形.
27.【答案】解:(Ⅰ)将k=1,b=1代入代入得:抛物线的解析式为y=ax2+x+1,直线的解析式为y=x. ∵y=ax2+x+1=a(x+
1
2??
)2+1﹣
1
4??
, ∴抛物线的顶点为(﹣
1
2??
,1﹣
1
4??
). ∵抛物线的顶点在直线y=x上, ∴﹣
1
2??
=1﹣
1
4??
,解得:a=﹣
1
4
. (Ⅱ)(i)将直线y=kx向上平移k2+1个单位,所得直线的解析式为y=kx+k2+1. ∵无论非零实数k取何值,直线与抛物线都只有一个交点, ∴方程kx+k2+1=ax2+bx+1有两个相等的实数根,即ax2+(b﹣k)x﹣k2=0有两个相等的实数根, ∴△=(b﹣k)2+4ak2=(4a+1)k2﹣2bk+b2=0. ∵无论非零实数k取何值时,(4a+1)k2﹣2bk+b2=0恒成立, ∴4a+1=0且b=0, ∴a=﹣
1
4
,b=0. ∴抛物线的解析式为y=﹣
1
4
x2+1. (ii)证明:根据题意,画出图象如图所示: / 设点P的坐标为(x,﹣
1
4
x2+1)则点Q的坐标为(x,2),D(x,0). ∴PD=|﹣
1
4
x2+1|,OD=|x|,QP=2﹣(﹣
1
4
x2+1)=
1
4
x2+1. 在Rt△OPD中,依据勾股定理得:OP=
??
2
+
(?
1
4
??
2
+1)
2
=
1
16
??
4
+
1
2
??
2
+1
=
1
4
x2+1. ∴OP=PQ
28.【答案】(1)解:①∵a=?
1
24
,P(0,1); ∴1=?
1
24
0?4
2
+h; ∴h=
5
3
; ②把x=5代入y=?
1
24
???4
2
+
5
3
得: y=?
1
24
5?4
2
+
5
3
=1.625; ∵1.625>1.55; ∴此球能过网. (2)解:把(0,1),(7,
12
5
)代入y=a
???4
2
+?得:;
16??+?=1
9??+?=
12
5
;解得:
??=?
1
5
?=
21
5
; ∴a=?
1
5
.
29.【答案】解:(1)∵点A在线段PQ的垂直平分线上, ∴AP = AQ. ∵∠DEF = 45°,∠ACB = 90°,∠DEF+∠ACB+∠EQC = 180°, ∴∠EQC = 45°. ∴∠DEF =∠EQC. ∴CE =" CQ." 由题意知:CE = t,BP ="2" t,?????????? ∴CQ = t. ∴AQ = 8-t. 在Rt△ABC中,由勾股定理得:AB =" 10" cm . 则AP = 10-2 t. ∴10-2 t = 8-t. 解得:t = 2. 答:当t =" 2" s时,点A在线段PQ的垂直平分线上.??????4分 (2)过P作????⊥????,交BE于M,∴∠??????=90°. / 在Rt△ABC和Rt△BPM中,sin??=
????
????
=
????
????
, ∴
????
2??
=
8
10
.??∴PM = ????=
8
5
??. ∵BC =" 6" cm,CE = t,?∴BE = 6-t. ∴y = S△ABC-S△BPE =
1
2
????·?????
1
2
????·????=
1
2
×6×8?
1
2
×
6???
×
8
5
?? =
4
5
??
2
?
24
5
??+24 =
4
5
(???3
)
2
+
84
5
. ∵??=
4
5
>0,∴抛物线开口向上. ∴当t = 3时,y最小=/. 答:当t = 3s时,四边形APEC的面积最小,最小面积为
84
5
cm2.?? 8分 (3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上. / 过P作????⊥????,交AC于N, ∴∠??????=∠??????=∠??????=90°. ∵∠??????=∠??????,∴△PAN ∽△BAC. ∴
????
????
=
????
????
=
????
????
. ∴
????
6
=
10?2??
10
=
????
8
. ∴????=6?
6
5
??,????=8?
8
5
??. ∵NQ = AQ-AN, ∴NQ = 8-t-(8?
8
5
??)=
3
5
??. ∵∠ACB = 90°,B、C(E)、F在同一条直线上, ∴∠QCF = 90°,∠QCF = ∠PNQ. ∵∠FQC = ∠PQN, ∴△QCF∽△QNP . ∴
????
????
=
????
????
.?∴
6?
6
5
??
9???
=
3
5
??
??
.? ∵06?
6
5
??
9???
=
3
5
解得:t = 1. 答:当t = 1s,点P、Q、F三点在同一条直线上.?
