青岛版九年级上《第二章解直角三角形》单元试卷(含答案)
文档属性
| 名称 | 青岛版九年级上《第二章解直角三角形》单元试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 149.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-26 19:24:32 | ||
图片预览



文档简介
【期末专题复习】青岛版九年级数学上册 第二章 解直角三角形 单元检测试卷
一、单选题(共10题;共30分)
1.计算:
sin
2
45°+
cos
2
45° 的值为(?? )
A.?
2
?????????????????????????????????????????/B.?
1
2
?????????????????????????????????????????/C.?1?????????????????????????????????????????/D.?
3
2.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为(?? )
A.?
3
5
??????????????????????????????????????????B.?
4
5
??????????????????????????????????????????C.?
3
4
??????????????????????????????????????????D.?
4
3
3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tanB=(?? ) /
A.??
3
2
?????????????????????????????????????/B.??
2
3
?????????????????????????????????????/C.??
6
2
?????????????????????????????????????/D.?
6
3
?
4.梯形护坡石坝的斜坡AB的坡度i=1:3,坝高BC为2米,则斜坡AB的长度是 () ???????????????????????????????????????????????????
A.?2
5
米?????????????????????????????????/B.?2
10
米?????????????????????????????????/C.?4
5
米?????????????????????????????????/D.?6米
5.在直角三角形中,如果各边都扩大1倍,则其锐角的三角函数值( )
A.?都扩大1倍????????????????????B.?都缩小为原来的一半????????????????????C.?都没有变化????????????????????D.?不能确定
6.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB的值等于(?? )
A.??
5
12
??????????????????????????????????????/B.?
12
5
??????????????????????????????????????/C.??
5
13
??????????????????????????????????????/D.?
12
13
7.下列各数中是有理数的是( )
A.?
3
3
???????????????????????????????????/B.?4π???????????????????????????????????/C.?sin45°???????????????????????????????????/D.?
1
cos60°
8.一上山坡路(如图所示),小明测得的数据如图中所示,则该坡路倾斜角α的正切值是(?? ) /
A.?
3
4
??????????????????????????????????????????B.?
4
3
??????????????????????????????????????????C.?
3
5
??????????????????????????????????????????D.?
4
5
9.已知在????????????中,∠??=
90
°
,∠??=??,????=3,那么????的长为(? ? ?? )
A.?3sin??;??????????????????????????????B.?3cos??;??????????????????????????????C.?
3
sin??
;??????????????????????????????D.?
3
cos??
.
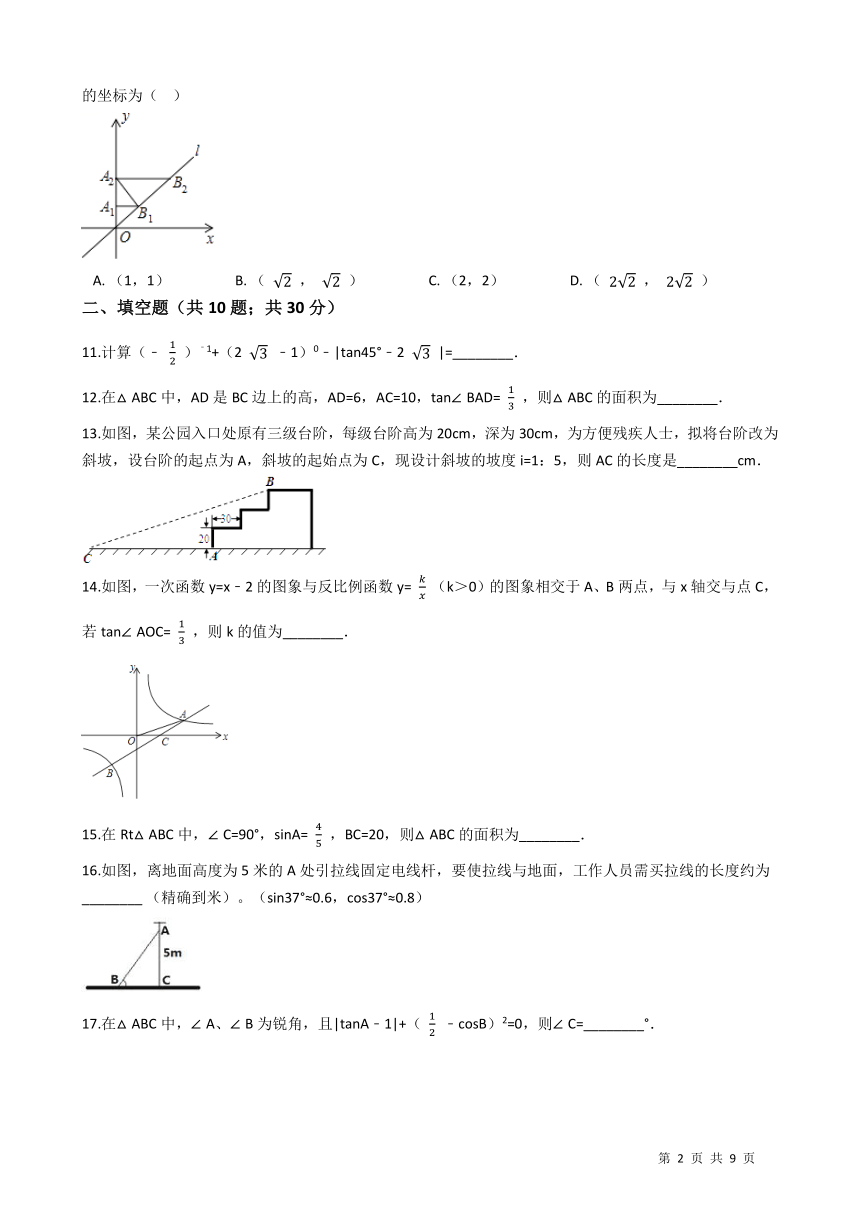
10.如图,在平面直角坐标系中,直线l所对应的函数表达式为y=x.过点A1(0,1)作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;过点A2作y轴的垂线交直线l于点B2 , 则点B2的坐标为(?? ) /
A.?(1,1)???????????????????B.?(
2
,
2
)???????????????????C.?(2,2)???????????????????D.?( 2
2
, 2
2
)
二、填空题(共10题;共30分)
11.计算(﹣
1
2
)﹣1+(2
3
﹣1)0﹣|tan45°﹣2
3
|=________.
12.在△ABC中,AD是BC边上的高,AD=6,AC=10,tan∠BAD=
1
3
,则△ABC的面积为________.
13.如图,某公园入口处原有三级台阶,每级台阶高为20cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡的坡度i=1:5,则AC的长度是________cm. /
14.如图,一次函数y=x﹣2的图象与反比例函数y=
??
??
(k>0)的图象相交于A、B两点,与x轴交与点C,若tan∠AOC=
1
3
,则k的值为________. /
15.在Rt△ABC中,∠C=90°,sinA=
4
5
,BC=20,则△ABC的面积为________.
16.如图,离地面高度为5米的A处引拉线固定电线杆,要使拉线与地面,工作人员需买拉线的长度约为________?(精确到米)。(sin37°≈0.6,cos37°≈0.8) /
17.在△ABC中,∠A、∠B为锐角,且|tanA﹣1|+(
1
2
﹣cosB)2=0,则∠C=________°.
18.如图所示,在△ABC中,∠C=90°,EF∥AB , ∠1=50°,则∠B的度数是________度. /
19.如图所示,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=13,BC=10,则sinC=________. /
20.如图,港口A在观测站O的正东方向,OA=4km , 某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为________km . ?
三、解答题(共8题;共60分)
21.计算:
12
?|?2|+
(1?
3
)
0
?9tan30°
22.如图为护城河改造前后河床的横断面示意图,将河床原竖直迎水面BC改建为坡度1:0.5的迎水坡AB,已知AB=4
5
米,则河床面的宽减少了多少米.(即求AC的长) /
23.中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶? 说明理由.(
3
≈1.732) /
24.如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:
2
≈1.4,
3
≈1.7) /
25.小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
26.如图,取一根9.5m长的标杆AB,在其上系一活动旗帜C,使标杆的影子落在平地和一堤坝的左斜坡上,拉动旗帜使其影子正好落在斜坡底角顶点D处.若测得旗高BC=4.5m,影长BD=9m,影长DE=5m,请计算左斜坡的坡比(假设标杆的影子BD,DE均与坝底线DM垂直).
/
27.如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果保留根号) /
28.如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计). 【参考数据:tan31°≈
3
5
,sin31°≈
1
2
,tan39°≈
9
11
,sin39°≈
7
11
】 /
答案解析部分
一、单选题
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】D
10.【答案】C
二、填空题
11.【答案】﹣2
3
12.【答案】18或30
13.【答案】240
14.【答案】3
15.【答案】150
16.【答案】8
17.【答案】75
18.【答案】40
19.【答案】
12
13
20.【答案】2 /?
三、解答题
21.【答案】 -1-
3
22.【答案】解:设AC的长为x,那么BC的长就为2x. x2+(2x)2=AB2 , x2+(2x)2=(4
5
)2 , x=4. 答:河床面的宽减少了4米.
23.【答案】解:过A作AD⊥CF于D, / 由题意得∠CAG=15°,∴∠ACE=15°, ∵∠ECF=75°,∴∠ACD=60°,在Rt△ACD中,sin∠ACD=
????
????
, 则AD=AC?sin∠ACD=250
3
≈433米,433米>400米,∴不需要改道. 答:消防车不需要改道行驶.
24.【答案】解:如图所示:过点C作CD⊥AB于点D, / 在Rt△ACD中,∠CAD=30°,AC=20km, 则CD=10km,AD=10
3
km, 在Rt△BCD中,∠CBD=45°,CD=10km, 故BD=10km,BC=10
2
km, 则AC+BC﹣AB=20+10
2
﹣10
3
﹣10≈7(km), 答:打通长江路后从A地道B地可少走7km的路程.
25.【答案】解:作AM⊥EF于点M,作BN⊥EF于点N,如右图所示, / 由题意可得,AM=BN=60米,CD=100米,∠ACF=45°,∠BDF=60°, ∴CM=
????
tan45°
=
60
1
=60 米, DN=
????
tan45°
=
60
3
=20
3
米, ∴AB=CD+DN﹣CM=100+20
3
﹣60=(40+20
3
)米, 即A、B两点的距离是40+20
3
米.
26.【答案】解:延长AE交BD的延长线于点F,作EG⊥DF,垂足为G,
/
∵DC∥AF,
∴△BCD∽△BAF.
∴
????
????
=
????
????
,
即
4.5
9.5
=
9
????
,
解得BF=19(m).
∵EG∥AB,
∴△FEG∽△DCB.
∴
????
????
=
????
????
,
即
????
4.5
=
????
9
,
解得FG=2EG.
设EG=x,则FG=2x,DG=19-9-2x=10-2x.
在Rt△DEG中,由勾股定理,得x2+(10-2x)2=52 ,
解得,x1=3,x2=5(舍去).
∴DG=4.
∴左斜坡的坡比i=
????
????
=3:4
27.【答案】解:设楼EF的高为x米,可得EG=EF﹣GF=(x﹣1.5)米, 依题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF(设垂足为G), 在Rt△EGD中,DG=
????
tan∠??????
=
3
3
(x﹣1.5)米,在Rt△EGB中,BG=
3
(x﹣1.5)米, ∴CA=DB=BG﹣DG=
2
3
3
(x﹣1.5)米, ∵CA=12米,∴
2
3
3
(x﹣1.5)=12, 解得:x=6
3
+1.5????????????????? 则楼EF的高度为6
3
+1.5米.
28.【答案】解:过点A作AD⊥BE于D, / 设山AD的高度为(x)m, 在Rt△ABD中, ∵∠ADB=90°,tan31°=
????
????
, ∴BD=
????
??????31°
≈
??
3
5
=
5
3
x, 在Rt△ACD中, ∵∠ADC=90°,tan39°=
????
????
, ∴CD=
????
??????39°
≈
??
9
11
=
11
9
x, ∵BC=BD﹣CD, ∴
5
3
x
11
9
x=80, 解得:x=180. 即山的高度为180米.
一、单选题(共10题;共30分)
1.计算:
sin
2
45°+
cos
2
45° 的值为(?? )
A.?
2
?????????????????????????????????????????/B.?
1
2
?????????????????????????????????????????/C.?1?????????????????????????????????????????/D.?
3
2.在Rt△ABC中,∠C=90°,BC=3,AB=4,则sinA的值为(?? )
A.?
3
5
??????????????????????????????????????????B.?
4
5
??????????????????????????????????????????C.?
3
4
??????????????????????????????????????????D.?
4
3
3.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tanB=(?? ) /
A.??
3
2
?????????????????????????????????????/B.??
2
3
?????????????????????????????????????/C.??
6
2
?????????????????????????????????????/D.?
6
3
?
4.梯形护坡石坝的斜坡AB的坡度i=1:3,坝高BC为2米,则斜坡AB的长度是 () ???????????????????????????????????????????????????
A.?2
5
米?????????????????????????????????/B.?2
10
米?????????????????????????????????/C.?4
5
米?????????????????????????????????/D.?6米
5.在直角三角形中,如果各边都扩大1倍,则其锐角的三角函数值( )
A.?都扩大1倍????????????????????B.?都缩小为原来的一半????????????????????C.?都没有变化????????????????????D.?不能确定
6.在△ABC中,若三边BC,CA,AB满足BC∶CA∶AB=5∶12∶13,则cosB的值等于(?? )
A.??
5
12
??????????????????????????????????????/B.?
12
5
??????????????????????????????????????/C.??
5
13
??????????????????????????????????????/D.?
12
13
7.下列各数中是有理数的是( )
A.?
3
3
???????????????????????????????????/B.?4π???????????????????????????????????/C.?sin45°???????????????????????????????????/D.?
1
cos60°
8.一上山坡路(如图所示),小明测得的数据如图中所示,则该坡路倾斜角α的正切值是(?? ) /
A.?
3
4
??????????????????????????????????????????B.?
4
3
??????????????????????????????????????????C.?
3
5
??????????????????????????????????????????D.?
4
5
9.已知在????????????中,∠??=
90
°
,∠??=??,????=3,那么????的长为(? ? ?? )
A.?3sin??;??????????????????????????????B.?3cos??;??????????????????????????????C.?
3
sin??
;??????????????????????????????D.?
3
cos??
.
10.如图,在平面直角坐标系中,直线l所对应的函数表达式为y=x.过点A1(0,1)作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;过点A2作y轴的垂线交直线l于点B2 , 则点B2的坐标为(?? ) /
A.?(1,1)???????????????????B.?(
2
,
2
)???????????????????C.?(2,2)???????????????????D.?( 2
2
, 2
2
)
二、填空题(共10题;共30分)
11.计算(﹣
1
2
)﹣1+(2
3
﹣1)0﹣|tan45°﹣2
3
|=________.
12.在△ABC中,AD是BC边上的高,AD=6,AC=10,tan∠BAD=
1
3
,则△ABC的面积为________.
13.如图,某公园入口处原有三级台阶,每级台阶高为20cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡的坡度i=1:5,则AC的长度是________cm. /
14.如图,一次函数y=x﹣2的图象与反比例函数y=
??
??
(k>0)的图象相交于A、B两点,与x轴交与点C,若tan∠AOC=
1
3
,则k的值为________. /
15.在Rt△ABC中,∠C=90°,sinA=
4
5
,BC=20,则△ABC的面积为________.
16.如图,离地面高度为5米的A处引拉线固定电线杆,要使拉线与地面,工作人员需买拉线的长度约为________?(精确到米)。(sin37°≈0.6,cos37°≈0.8) /
17.在△ABC中,∠A、∠B为锐角,且|tanA﹣1|+(
1
2
﹣cosB)2=0,则∠C=________°.
18.如图所示,在△ABC中,∠C=90°,EF∥AB , ∠1=50°,则∠B的度数是________度. /
19.如图所示,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=13,BC=10,则sinC=________. /
20.如图,港口A在观测站O的正东方向,OA=4km , 某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为________km . ?
三、解答题(共8题;共60分)
21.计算:
12
?|?2|+
(1?
3
)
0
?9tan30°
22.如图为护城河改造前后河床的横断面示意图,将河床原竖直迎水面BC改建为坡度1:0.5的迎水坡AB,已知AB=4
5
米,则河床面的宽减少了多少米.(即求AC的长) /
23.中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶? 说明理由.(
3
≈1.732) /
24.如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:
2
≈1.4,
3
≈1.7) /
25.小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
26.如图,取一根9.5m长的标杆AB,在其上系一活动旗帜C,使标杆的影子落在平地和一堤坝的左斜坡上,拉动旗帜使其影子正好落在斜坡底角顶点D处.若测得旗高BC=4.5m,影长BD=9m,影长DE=5m,请计算左斜坡的坡比(假设标杆的影子BD,DE均与坝底线DM垂直).
/
27.如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果保留根号) /
28.如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计). 【参考数据:tan31°≈
3
5
,sin31°≈
1
2
,tan39°≈
9
11
,sin39°≈
7
11
】 /
答案解析部分
一、单选题
1.【答案】C
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】D
10.【答案】C
二、填空题
11.【答案】﹣2
3
12.【答案】18或30
13.【答案】240
14.【答案】3
15.【答案】150
16.【答案】8
17.【答案】75
18.【答案】40
19.【答案】
12
13
20.【答案】2 /?
三、解答题
21.【答案】 -1-
3
22.【答案】解:设AC的长为x,那么BC的长就为2x. x2+(2x)2=AB2 , x2+(2x)2=(4
5
)2 , x=4. 答:河床面的宽减少了4米.
23.【答案】解:过A作AD⊥CF于D, / 由题意得∠CAG=15°,∴∠ACE=15°, ∵∠ECF=75°,∴∠ACD=60°,在Rt△ACD中,sin∠ACD=
????
????
, 则AD=AC?sin∠ACD=250
3
≈433米,433米>400米,∴不需要改道. 答:消防车不需要改道行驶.
24.【答案】解:如图所示:过点C作CD⊥AB于点D, / 在Rt△ACD中,∠CAD=30°,AC=20km, 则CD=10km,AD=10
3
km, 在Rt△BCD中,∠CBD=45°,CD=10km, 故BD=10km,BC=10
2
km, 则AC+BC﹣AB=20+10
2
﹣10
3
﹣10≈7(km), 答:打通长江路后从A地道B地可少走7km的路程.
25.【答案】解:作AM⊥EF于点M,作BN⊥EF于点N,如右图所示, / 由题意可得,AM=BN=60米,CD=100米,∠ACF=45°,∠BDF=60°, ∴CM=
????
tan45°
=
60
1
=60 米, DN=
????
tan45°
=
60
3
=20
3
米, ∴AB=CD+DN﹣CM=100+20
3
﹣60=(40+20
3
)米, 即A、B两点的距离是40+20
3
米.
26.【答案】解:延长AE交BD的延长线于点F,作EG⊥DF,垂足为G,
/
∵DC∥AF,
∴△BCD∽△BAF.
∴
????
????
=
????
????
,
即
4.5
9.5
=
9
????
,
解得BF=19(m).
∵EG∥AB,
∴△FEG∽△DCB.
∴
????
????
=
????
????
,
即
????
4.5
=
????
9
,
解得FG=2EG.
设EG=x,则FG=2x,DG=19-9-2x=10-2x.
在Rt△DEG中,由勾股定理,得x2+(10-2x)2=52 ,
解得,x1=3,x2=5(舍去).
∴DG=4.
∴左斜坡的坡比i=
????
????
=3:4
27.【答案】解:设楼EF的高为x米,可得EG=EF﹣GF=(x﹣1.5)米, 依题意得:EF⊥AF,DC⊥AF,BA⊥AF,BD⊥EF(设垂足为G), 在Rt△EGD中,DG=
????
tan∠??????
=
3
3
(x﹣1.5)米,在Rt△EGB中,BG=
3
(x﹣1.5)米, ∴CA=DB=BG﹣DG=
2
3
3
(x﹣1.5)米, ∵CA=12米,∴
2
3
3
(x﹣1.5)=12, 解得:x=6
3
+1.5????????????????? 则楼EF的高度为6
3
+1.5米.
28.【答案】解:过点A作AD⊥BE于D, / 设山AD的高度为(x)m, 在Rt△ABD中, ∵∠ADB=90°,tan31°=
????
????
, ∴BD=
????
??????31°
≈
??
3
5
=
5
3
x, 在Rt△ACD中, ∵∠ADC=90°,tan39°=
????
????
, ∴CD=
????
??????39°
≈
??
9
11
=
11
9
x, ∵BC=BD﹣CD, ∴
5
3
x
11
9
x=80, 解得:x=180. 即山的高度为180米.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
