人教高中数学选修2-1第二章 2.4.2抛物线焦点弦的性质(共20张PPT)
文档属性
| 名称 | 人教高中数学选修2-1第二章 2.4.2抛物线焦点弦的性质(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 566.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-27 22:59:38 | ||
图片预览




文档简介
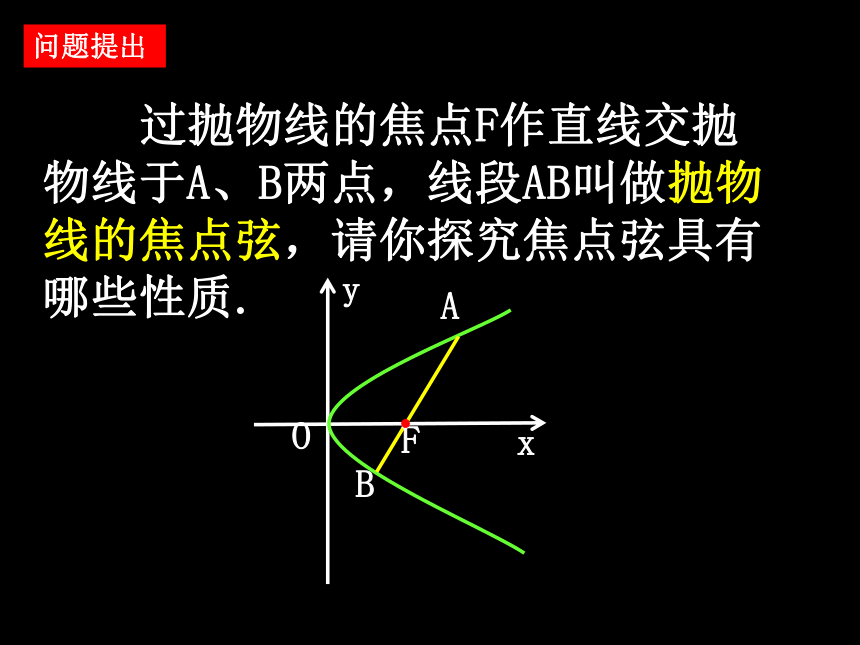
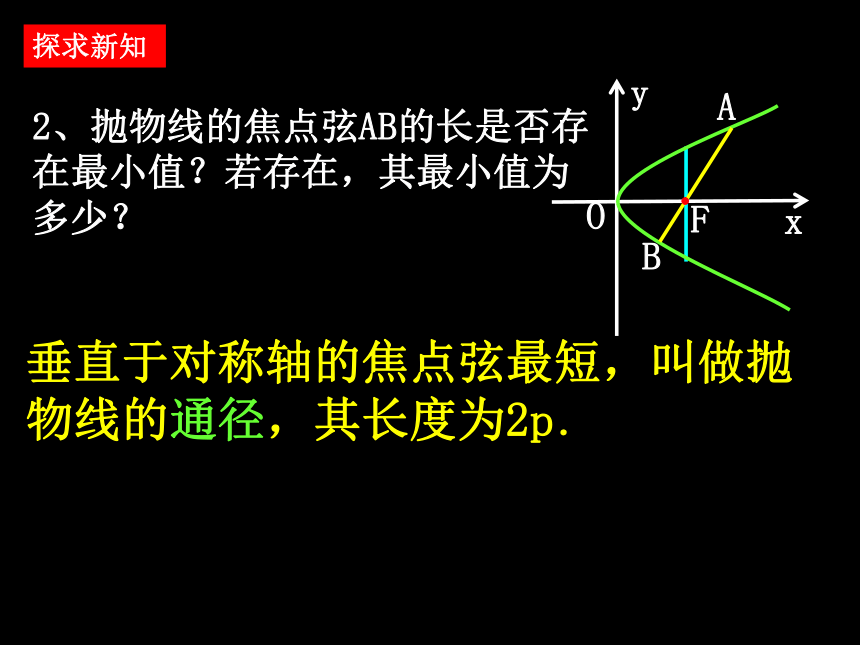
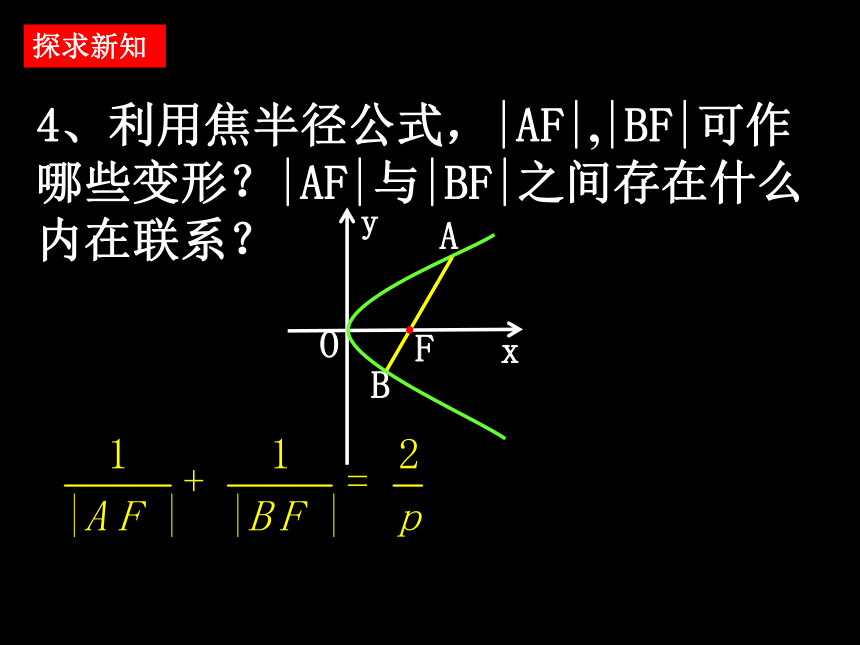
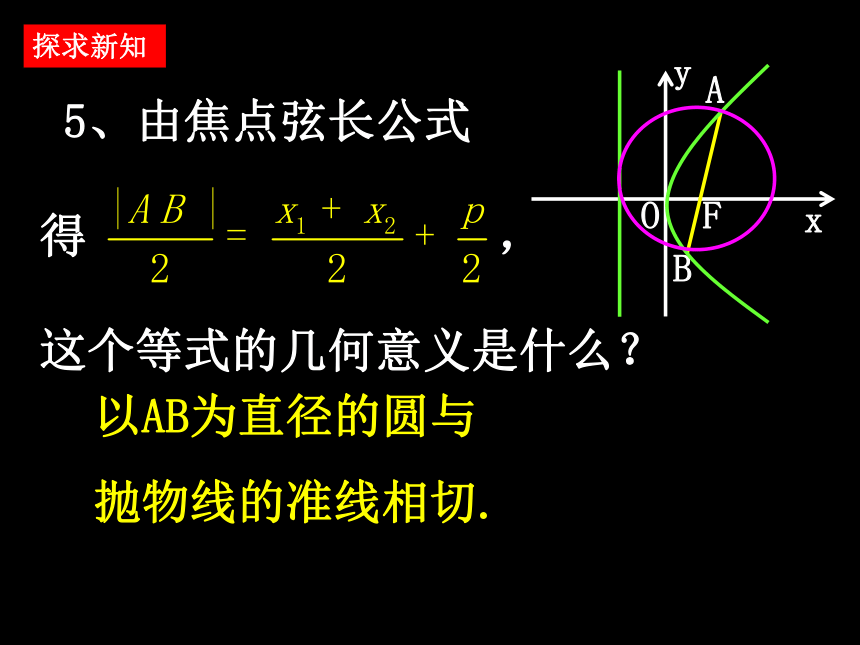
课件20张PPT。2.4.2抛物线的几何性质抛物线焦点弦的性质 1.抛物线y2=2px(p>0)的范围、对称性、顶点、离心率、焦半径分别是什么? 范围:x≥0,y∈R; 对称性:关于x轴对称; 顶点:原点; 离心率:e=1; 复习回顾 过抛物线的焦点F作直线交抛物线于A、B两点,线段AB叫做抛物线的焦点弦,请你探究焦点弦具有哪些性质.问题提出1、焦点弦AB的长如何计算? 设AB为焦点弦.点A(x1,y1),B(x2,y2) |AB|=x1+x2+p 探求新知2、抛物线的焦点弦AB的长是否存在最小值?若存在,其最小值为多少?垂直于对称轴的焦点弦最短,叫做抛物线的通径,其长度为2p.探求新知3、A、B两点的坐标是否存在相关关系?若存在,其坐标之间的关系如何?探求新知4、利用焦半径公式,|AF|,|BF|可作哪些变形?|AF|与|BF|之间存在什么内在联系?探求新知以AB为直径的圆与
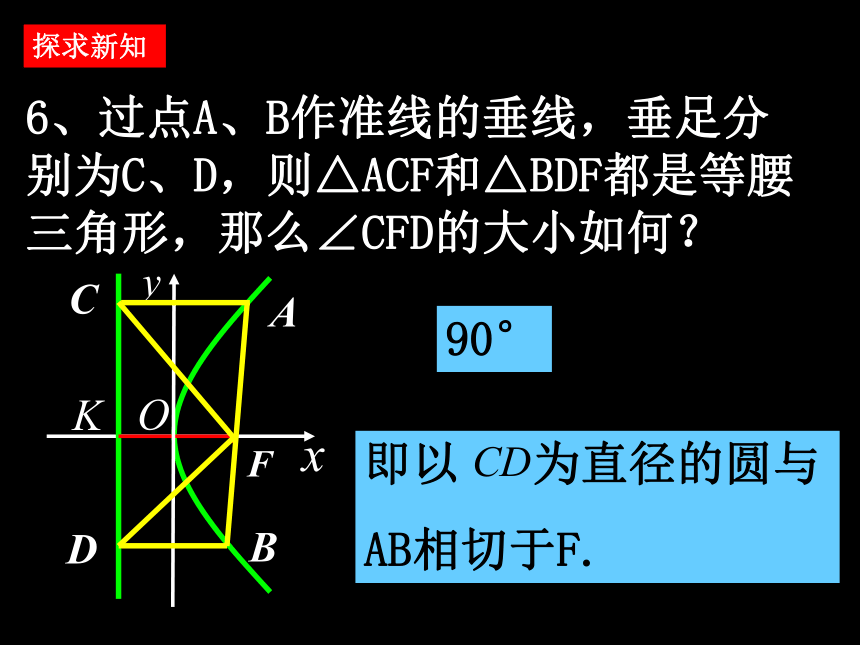
抛物线的准线相切.探求新知6、过点A、B作准线的垂线,垂足分别为C、D,则△ACF和△BDF都是等腰三角形,那么∠CFD的大小如何? 90° 探求新知7、过点A、B作准线的垂线,垂足分别为C、D,A、O、D三点共线吗? 探求新知8、若直线AO交准线于D,DB与X轴平行吗? 探求新知9、设点M为抛物线准线与x轴的交点,
则∠AMF与∠BMF的大小关系如何? 相等 探求新知 过抛物线y2=2px的焦点F作直线交抛物线于A、B两点,焦点弦AB具有如下性质.形成结论OBAFCDM例题8244p 例1 过抛物线焦点F的直线交抛物线于A、B两点,过点A和抛物线顶点的直线交抛物线的准线于点C,求证:直线BC平行于抛物线的对称轴. 例题讲解例题讲解例题讲解OBAOBA例题讲解例题讲解课堂小结1.抛物线有许多几何性质,探究抛物线的几何性质,可作为一个研究性学习课题,其中焦点弦性质中的有些结论会对解题有一定的帮助.2.焦点弦性质y1y2=-p2是对焦点在x轴上的抛物线而言的,对焦点在y轴上的抛物线,类似地有x1x2=-p2.
抛物线的准线相切.探求新知6、过点A、B作准线的垂线,垂足分别为C、D,则△ACF和△BDF都是等腰三角形,那么∠CFD的大小如何? 90° 探求新知7、过点A、B作准线的垂线,垂足分别为C、D,A、O、D三点共线吗? 探求新知8、若直线AO交准线于D,DB与X轴平行吗? 探求新知9、设点M为抛物线准线与x轴的交点,
则∠AMF与∠BMF的大小关系如何? 相等 探求新知 过抛物线y2=2px的焦点F作直线交抛物线于A、B两点,焦点弦AB具有如下性质.形成结论OBAFCDM例题8244p 例1 过抛物线焦点F的直线交抛物线于A、B两点,过点A和抛物线顶点的直线交抛物线的准线于点C,求证:直线BC平行于抛物线的对称轴. 例题讲解例题讲解例题讲解OBAOBA例题讲解例题讲解课堂小结1.抛物线有许多几何性质,探究抛物线的几何性质,可作为一个研究性学习课题,其中焦点弦性质中的有些结论会对解题有一定的帮助.2.焦点弦性质y1y2=-p2是对焦点在x轴上的抛物线而言的,对焦点在y轴上的抛物线,类似地有x1x2=-p2.
