2010江苏高邮赞化学校中考二轮复习-----探讨开放探究性试题解决的方法与策略
文档属性
| 名称 | 2010江苏高邮赞化学校中考二轮复习-----探讨开放探究性试题解决的方法与策略 |

|
|
| 格式 | rar | ||
| 文件大小 | 74.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 化学 | ||
| 更新时间 | 2010-08-23 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
阅 读 理 解 题
班级: 姓名: 学号:
学习目标
阅读理解试题要求考生能透彻理解课本中的所学内容,善于总结解题规律,并能准确阐述自己的思想和观点,考查学生对数学知识的理解水平、数学方法的运用水平及分析推理能力、数据处理能力、文字概括能力、书面表达能力、随机应变能力和知识的迁移能力等.
学习难点
透彻理解所学内容.搞清楚知识的来龙去脉,掌握在研究知识的过程中体现出的数学思想和方法.
教学过程
一、概念型的阅读题
这类试题首先给出一个末知的定义、公式、定理、性质或计算法则,然后据此解决题目中提出的问题.
【例1】(2009年益阳市)阅读材料:
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
二、解题方法型阅读题
主要介绍题某一类题的解题方法,要求考生利用例题中的解题方法且能够模仿例题的解题步骤解答一道与例题类似的问题.
【例2】(2009年邵阳市)阅读下列材料,然后回答问题.
在进行二次根式运算时,我们有时会碰上如 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 一样的式子,其实我们还可以将其进一步化简:
; (Ⅰ)
HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 (Ⅱ)
. (Ⅲ)
以上这种化简的步骤叫做分母有理化.
HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 还可以用以下方法化简:
. (Ⅳ)
(1)请用不同的方法化简 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 .
①参照(Ⅲ)式得=___________________________________________.
②参照(Ⅳ)式得 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 =___________________________________________.
(2)化简:.
三、图象型的阅读题
图形和图象是最直观、最形象的数学语言,它包含着丰富的信息资源.要求学生能根据实际问题中所呈现出来的图形、图象的信息,通过分析、加工等手段解决问题.
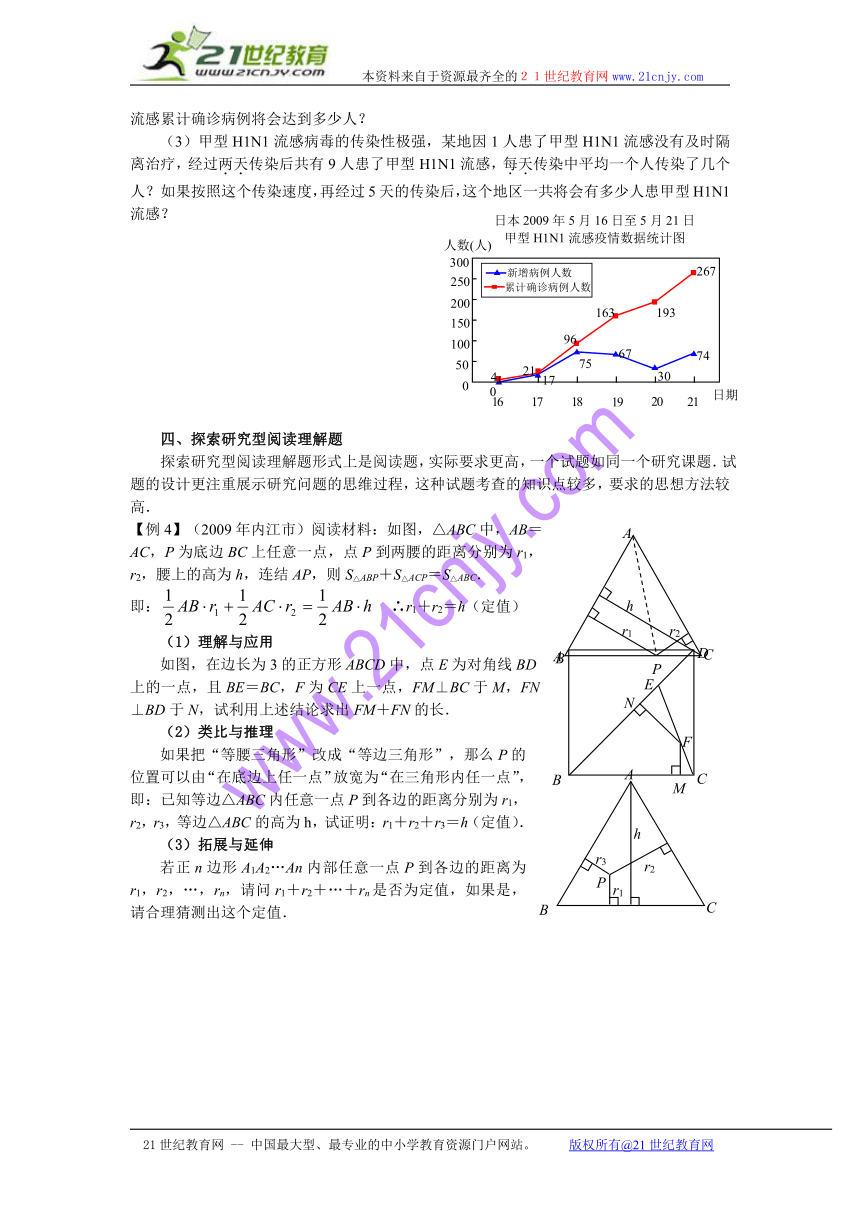
【例3】(2009年衢州市)2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
(1)在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
(2)在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(3)甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
四、探索研究型阅读理解题
探索研究型阅读理解题形式上是阅读题,实际要求更高,一个试题如同一个研究课题.试题的设计更注重展示研究问题的思维过程,这种试题考查的知识点较多,要求的思想方法较高.
【例4】(2009年内江市)阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连结AP,则S△ABP+S△ACP=S△ABC.
即: HYPERLINK " http://www.21cnjy.com" EMBED Equation.KSEE3 ∴r1+r2=h(定值)
(1)理解与应用
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明:r1+r2+r3=h(定值).
(3)拓展与延伸
若正n边形A1A2…An内部任意一点P到各边的距离为r1,r2,…,rn,请问r1+r2+…+rn是否为定值,如果是,请合理猜测出这个定值.
【课后作业】
班级 姓名 学号
1.(2009年鄂州市)为了求1+2+22+23+…+22008的值,可令S=1+2+22+23+…+22008,则2 S=2+22+23+24+…+22009,因此2S-S=22009-1,所以1+2+22+23+…+22008=22009-1.仿照以上推理计算出1+5+52+53+…+52009的值是( )
A. B. C. D.
2.(2008年贵阳市)符号“f”表示一种运算,它对一些数的运算结果如下:(1)f(1)=0,f(2)=1,f(3)=2,f(4)=3,…(2), HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 ,, HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 ,…
利用以上规律计算: .
3.(2009年中山市)小明用下面的方法求出方程 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
方程 换元法得新方程 解新方程 检验 求原方程的解
令 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 则 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 所以
HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4
4.(2009年漳州市)阅读材料,解答问题.
例:用图象法解一元二次不等式:x2-2x-3>0.
解:设y=x2-2x-3,则y是x的二次函数.
∵a=1>0, ∴抛物线开口向上.
又当y=0时,x2-2x-3=0,解得x1=-1,x2=3.
∴由此得抛物线y=x2-2x-3的大致图象如图所示.
观察函数图象可知:当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是:x<-1或x>3.
(1)观察图象,直接写出一元二次不等式:x2-2x-3<0的解集是____________;
(2)仿照上例,用图象法解一元二次不等式:x2-1>0.
5.(2009年山西省)根据山西省统计信息网公布的数据,绘制了山西省2004~2008固定电话和移动电话年末用户条形统计图如下:
(1)填空:2004~2008移动电话年末用户的极差是 万户,固定电话年末用户的中位数是 万户;
(2)你还能从图中获取哪些信息?请写出两条.
6.(2009年济宁市)阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线l的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线m:y=kx+t(t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
7.(2009年咸宁市)问题背景:
在△ABC中,AB、BC、AC三边的长分别为 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 、、 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 ,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上.__________________
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为、 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 、(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新:
(3)若△ABC三边的长分别为 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 、、 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 (,且 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 ),试运用构图法求出这三角形的面积.
8.(2009年河北省)
如图1至图5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c.
阅读理解:
(1)如图1,⊙O从⊙O1的位置出发,沿AB滚动到
⊙O2的位置,当AB = c时,⊙O恰好自转1周.
(2)如图2,∠ABC相邻的补角是n°,⊙O在
∠ABC外部沿A-B-C滚动,在点B处,必须由
⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋
转的角∠O1BO2 = n°,⊙O在点B处自转 ( http: / / www.21cnjy.com )周.
实践应用:
(1)在阅读理解的(1)中,若AB = 2c,则⊙O自转 周; 若AB= l,则⊙O自转 周.在阅读理解的(2)中,若∠ABC =120°,则⊙O在点B处自转 周;若∠ABC =60°,则⊙O在点B处自转 周.
(2)如图3,∠ABC=90°,AB=BC=c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.
拓展联想:
(1)如图4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
(2)如图5,多边形的周长为l,⊙O从与某边相切于
点D的位置出发,在多边形外部,按顺时针方向沿多
边形滚动,又回到与该边相切于点D的位置,直接写
出⊙O自转的周数.
图2
x
C
O
y
A
B
D
1
1
B
C
铅垂高
水平宽
h
a
图1
累计确诊病例人数
新增病例人数
0
4
21
96
163
193
267
17
75
67
30
74
16
17
18
19
20
21
日本2009年5月16日至5月21日
甲型H1N1流感疫情数据统计图
人数(人)
0
50
100
150
200
250
300
日期
A
C
B
P
r1
r2
h
D
C
B
A
E
N
F
M
C
A
B
P
r1
r3
r2
h
1
2
3
1
2
3
x
y
0
200
400
600
800
1000
1200
1400
1600
1800
年份
万户
固定电话年末用户
移动电话年末用户
2004
2005
2006
2007
2008
721.3
753.8
897.8
906.2
885.4
989.6
859.0
1420.4
1689.5
803.0
第5题图
y
x
2
4
6
2
4
6
-2
-2
第6题图
O
(图①)
(图②)
第7题图
A
C
B
图1
A
O1
O
O2
B
B
图2
A
C
n°
D
O1
O2
B
图3
O2
O3
O
A
O1
C
O4
O
A
B
C
图4
D
D
图5
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
阅 读 理 解 题
班级: 姓名: 学号:
学习目标
阅读理解试题要求考生能透彻理解课本中的所学内容,善于总结解题规律,并能准确阐述自己的思想和观点,考查学生对数学知识的理解水平、数学方法的运用水平及分析推理能力、数据处理能力、文字概括能力、书面表达能力、随机应变能力和知识的迁移能力等.
学习难点
透彻理解所学内容.搞清楚知识的来龙去脉,掌握在研究知识的过程中体现出的数学思想和方法.
教学过程
一、概念型的阅读题
这类试题首先给出一个末知的定义、公式、定理、性质或计算法则,然后据此解决题目中提出的问题.
【例1】(2009年益阳市)阅读材料:
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
(3)是否存在一点P,使S△PAB=S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
二、解题方法型阅读题
主要介绍题某一类题的解题方法,要求考生利用例题中的解题方法且能够模仿例题的解题步骤解答一道与例题类似的问题.
【例2】(2009年邵阳市)阅读下列材料,然后回答问题.
在进行二次根式运算时,我们有时会碰上如 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 一样的式子,其实我们还可以将其进一步化简:
; (Ⅰ)
HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 (Ⅱ)
. (Ⅲ)
以上这种化简的步骤叫做分母有理化.
HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 还可以用以下方法化简:
. (Ⅳ)
(1)请用不同的方法化简 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 .
①参照(Ⅲ)式得=___________________________________________.
②参照(Ⅳ)式得 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 =___________________________________________.
(2)化简:.
三、图象型的阅读题
图形和图象是最直观、最形象的数学语言,它包含着丰富的信息资源.要求学生能根据实际问题中所呈现出来的图形、图象的信息,通过分析、加工等手段解决问题.
【例3】(2009年衢州市)2009年5月17日至21日,甲型H1N1流感在日本迅速蔓延,每天的新增病例和累计确诊病例人数如图所示.
(1)在5月17日至5月21日这5天中,日本新增甲型H1N1流感病例最多的是哪一天?该天增加了多少人?
(2)在5月17日至5月21日这5天中,日本平均每天新增加甲型H1N1流感确诊病例多少人?如果接下来的5天中,继续按这个平均数增加,那么到5月26日,日本甲型H1N1流感累计确诊病例将会达到多少人?
(3)甲型H1N1流感病毒的传染性极强,某地因1人患了甲型H1N1流感没有及时隔离治疗,经过两天传染后共有9人患了甲型H1N1流感,每天传染中平均一个人传染了几个人?如果按照这个传染速度,再经过5天的传染后,这个地区一共将会有多少人患甲型H1N1流感?
四、探索研究型阅读理解题
探索研究型阅读理解题形式上是阅读题,实际要求更高,一个试题如同一个研究课题.试题的设计更注重展示研究问题的思维过程,这种试题考查的知识点较多,要求的思想方法较高.
【例4】(2009年内江市)阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连结AP,则S△ABP+S△ACP=S△ABC.
即: HYPERLINK " http://www.21cnjy.com" EMBED Equation.KSEE3 ∴r1+r2=h(定值)
(1)理解与应用
如图,在边长为3的正方形ABCD中,点E为对角线BD上的一点,且BE=BC,F为CE上一点,FM⊥BC于M,FN⊥BD于N,试利用上述结论求出FM+FN的长.
(2)类比与推理
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明:r1+r2+r3=h(定值).
(3)拓展与延伸
若正n边形A1A2…An内部任意一点P到各边的距离为r1,r2,…,rn,请问r1+r2+…+rn是否为定值,如果是,请合理猜测出这个定值.
【课后作业】
班级 姓名 学号
1.(2009年鄂州市)为了求1+2+22+23+…+22008的值,可令S=1+2+22+23+…+22008,则2 S=2+22+23+24+…+22009,因此2S-S=22009-1,所以1+2+22+23+…+22008=22009-1.仿照以上推理计算出1+5+52+53+…+52009的值是( )
A. B. C. D.
2.(2008年贵阳市)符号“f”表示一种运算,它对一些数的运算结果如下:(1)f(1)=0,f(2)=1,f(3)=2,f(4)=3,…(2), HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 ,, HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 ,…
利用以上规律计算: .
3.(2009年中山市)小明用下面的方法求出方程 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
方程 换元法得新方程 解新方程 检验 求原方程的解
令 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 则 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 所以
HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4
4.(2009年漳州市)阅读材料,解答问题.
例:用图象法解一元二次不等式:x2-2x-3>0.
解:设y=x2-2x-3,则y是x的二次函数.
∵a=1>0, ∴抛物线开口向上.
又当y=0时,x2-2x-3=0,解得x1=-1,x2=3.
∴由此得抛物线y=x2-2x-3的大致图象如图所示.
观察函数图象可知:当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是:x<-1或x>3.
(1)观察图象,直接写出一元二次不等式:x2-2x-3<0的解集是____________;
(2)仿照上例,用图象法解一元二次不等式:x2-1>0.
5.(2009年山西省)根据山西省统计信息网公布的数据,绘制了山西省2004~2008固定电话和移动电话年末用户条形统计图如下:
(1)填空:2004~2008移动电话年末用户的极差是 万户,固定电话年末用户的中位数是 万户;
(2)你还能从图中获取哪些信息?请写出两条.
6.(2009年济宁市)阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数y=k1x+b1(k1≠0)的图象为直线l1,一次函数y=k2x+b2(k2≠0)的图象为直线l2,若k1=k2,且b1≠b2,我们就称直线l1与直线l2互相平行.
解答下面的问题:
(1)求过点P(1,4)且与已知直线y=-2x-1平行的直线l的函数表达式,并画出直线l的图象;
(2)设直线l分别与y轴、x轴交于点A、B,如果直线m:y=kx+t(t>0)与直线l平行且交x轴于点C,求出△ABC的面积S关于t的函数表达式.
7.(2009年咸宁市)问题背景:
在△ABC中,AB、BC、AC三边的长分别为 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 、、 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 ,求这个三角形的面积.
小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上.__________________
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为、 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 、(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新:
(3)若△ABC三边的长分别为 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 、、 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 (,且 HYPERLINK " http://www.21cnjy.com" EMBED Equation.DSMT4 ),试运用构图法求出这三角形的面积.
8.(2009年河北省)
如图1至图5,⊙O均作无滑动滚动,⊙O1、⊙O2、⊙O3、⊙O4均表示⊙O与线段AB或BC相切于端点时刻的位置,⊙O的周长为c.
阅读理解:
(1)如图1,⊙O从⊙O1的位置出发,沿AB滚动到
⊙O2的位置,当AB = c时,⊙O恰好自转1周.
(2)如图2,∠ABC相邻的补角是n°,⊙O在
∠ABC外部沿A-B-C滚动,在点B处,必须由
⊙O1的位置旋转到⊙O2的位置,⊙O绕点B旋
转的角∠O1BO2 = n°,⊙O在点B处自转 ( http: / / www.21cnjy.com )周.
实践应用:
(1)在阅读理解的(1)中,若AB = 2c,则⊙O自转 周; 若AB= l,则⊙O自转 周.在阅读理解的(2)中,若∠ABC =120°,则⊙O在点B处自转 周;若∠ABC =60°,则⊙O在点B处自转 周.
(2)如图3,∠ABC=90°,AB=BC=c.⊙O从⊙O1的位置出发,在∠ABC外部沿A-B-C滚动到⊙O4的位置,⊙O自转 周.
拓展联想:
(1)如图4,△ABC的周长为l,⊙O从与AB相切于点D的位置出发,在△ABC外部,按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,⊙O自转了多少周?请说明理由.
(2)如图5,多边形的周长为l,⊙O从与某边相切于
点D的位置出发,在多边形外部,按顺时针方向沿多
边形滚动,又回到与该边相切于点D的位置,直接写
出⊙O自转的周数.
图2
x
C
O
y
A
B
D
1
1
B
C
铅垂高
水平宽
h
a
图1
累计确诊病例人数
新增病例人数
0
4
21
96
163
193
267
17
75
67
30
74
16
17
18
19
20
21
日本2009年5月16日至5月21日
甲型H1N1流感疫情数据统计图
人数(人)
0
50
100
150
200
250
300
日期
A
C
B
P
r1
r2
h
D
C
B
A
E
N
F
M
C
A
B
P
r1
r3
r2
h
1
2
3
1
2
3
x
y
0
200
400
600
800
1000
1200
1400
1600
1800
年份
万户
固定电话年末用户
移动电话年末用户
2004
2005
2006
2007
2008
721.3
753.8
897.8
906.2
885.4
989.6
859.0
1420.4
1689.5
803.0
第5题图
y
x
2
4
6
2
4
6
-2
-2
第6题图
O
(图①)
(图②)
第7题图
A
C
B
图1
A
O1
O
O2
B
B
图2
A
C
n°
D
O1
O2
B
图3
O2
O3
O
A
O1
C
O4
O
A
B
C
图4
D
D
图5
O
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
