苏科版九年级数学下册期末专题复习《第七章锐角三角函数》单元评估检测试卷(有答案)
文档属性
| 名称 | 苏科版九年级数学下册期末专题复习《第七章锐角三角函数》单元评估检测试卷(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 137.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-29 00:00:00 | ||
图片预览



文档简介
期末专题复习:苏科版九年级数学下册 第七章 锐角三角函数 单元评估检测试卷
一、单选题(共10题;共30分)
1.把三角形三边的长度都扩大为原来的2倍,则锐角A的正弦函数值(????)
A.?扩大为原来的2倍??????????????????????/B.?缩小为原来的
1
2
??????????????????????/C.?不变??????????????????????/D.?不能确定
2.在△ABC中,∠C=90°,sinA=
3
2
,则cosB的值为(??? )
A.?1????????????????????????????????????????/B.?
3
2
????????????????????????????????????????/C.?
2
2
????????????????????????????????????????/D.?
1
2
3.△ABC中,∠C=90°,BC=12,AB=13,那么sinA的值等于(????)
A.?
5
13
???????????????????????????????????????/B.?
12
13
???????????????????????????????????????/C.?
5
12
???????????????????????????????????????/D.?
12
5
4.(2016?陕西)已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为(? )
A.?
1
2
????????????????????????????????????????/B.?
5
5
????????????????????????????????????????/C.?
2
5
5
????????????????????????????????????????/D.?2
5.如图,小明要测量河内小岛 B 到河边公路 l 的距离,在 A 点测得∠BAD=30°,在 C 点测得∠BCD=60°,又测得 AC=60米,则小岛 B 到公路 l 的距离为( ) /
A.?30 米?????????????????????????/B.?30
3
米?????????????????????????/C.?40
3
米?????????????????????????/D.?(30+
3
)米
6.Rt△ABC中,∠C=90°,AB=13,AC=5,则sinB的值为( )
A.?
5
13
???/B.?
13
5
?/C.?
12
13
?/D.?
5
12
7.若α是锐角,tanα?tan50°=1,则α的值为(?? )
A.?20°???????????????????????????????????????B.?30°???????????????????????????????????????C.?40°???????????????????????????????????????D.?50°
8.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为(?? ) /
A.?
1
2
???????????????????????????????????????/B.?
3
3
???????????????????????????????????????/C.?
2
2
???????????????????????????????????????/D.?
3
2
9.如图,某侦察机在空中A处发现敌方地面目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=4500米,tanα=
5
6
, 则飞机到目标B的水平距离BC为( ) /
A.?5400
5
米????????????????????????/B.?5400
3
米????????????????????????/C.?5600
5
米????????????????????????/D.?5600
3
米
10.(2017?绵阳)如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2
3
,∠AEO=120°,则FC的长度为(?? ) /
A.?1?????????????????????????????????????????/B.?2?????????????????????????????????????????/C.?
2
?????????????????????????????????????????/D.?
3
二、填空题(共10题;共30分)
11.在△ABC中,∠C=90°,sinA= /,则tanB=________.
12.如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为________米.( sin56°≈0.8 , tan56°≈1.5 ) /
13.已知 ?? 为锐角,且 tan
???
10
°
=
3
3
,则锐角 ?? 的度数是________.
14.在菱形ABCD中,DE⊥AB,cosA=
3
5
,BE=2,则tan∠DBE的值是________. /
15.已知α是锐角且tanα=
3
4
, 则sinα+cosα=________?
16.如图,某公园入口处原有三级台阶,每级台阶高为20cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡的坡度i=1:5,则AC的长度是________cm. /
17.在以O为坐标原点的直角坐标平面内有一点A(2,4),如果AO与x轴正半轴的夹角为α,那么sinα=________ .
18.在△ABC中,AB=AC=10,cosB=
3
5
,如果圆O的半径为2
10
,且经过点B、C,那么线段AO的长等于________.
19.如果一个四边形的某个顶点到其他三个顶点的距离相等,我们把这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.如图,已知梯形ABCD是等距四边形,AB//CD,点B是等距点. 若BC=10, cos??=
10
10
,则CD的长等于________. /
20.如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F。若tanA=
1
2
,则
????
????
=________。如图 2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F。若
????
????
=
1
3
,tanA=
1
2
,则
????
????
=________。 //
三、解答题(共8题;共60分)
21.(2017·金华)(本题6分)计算:2cos60°+(?1)2017+|?3|?(2?1)0.
22.如图,从热气球C处测得地面A,B两点的俯角分别为 30° , 45° ,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离. /
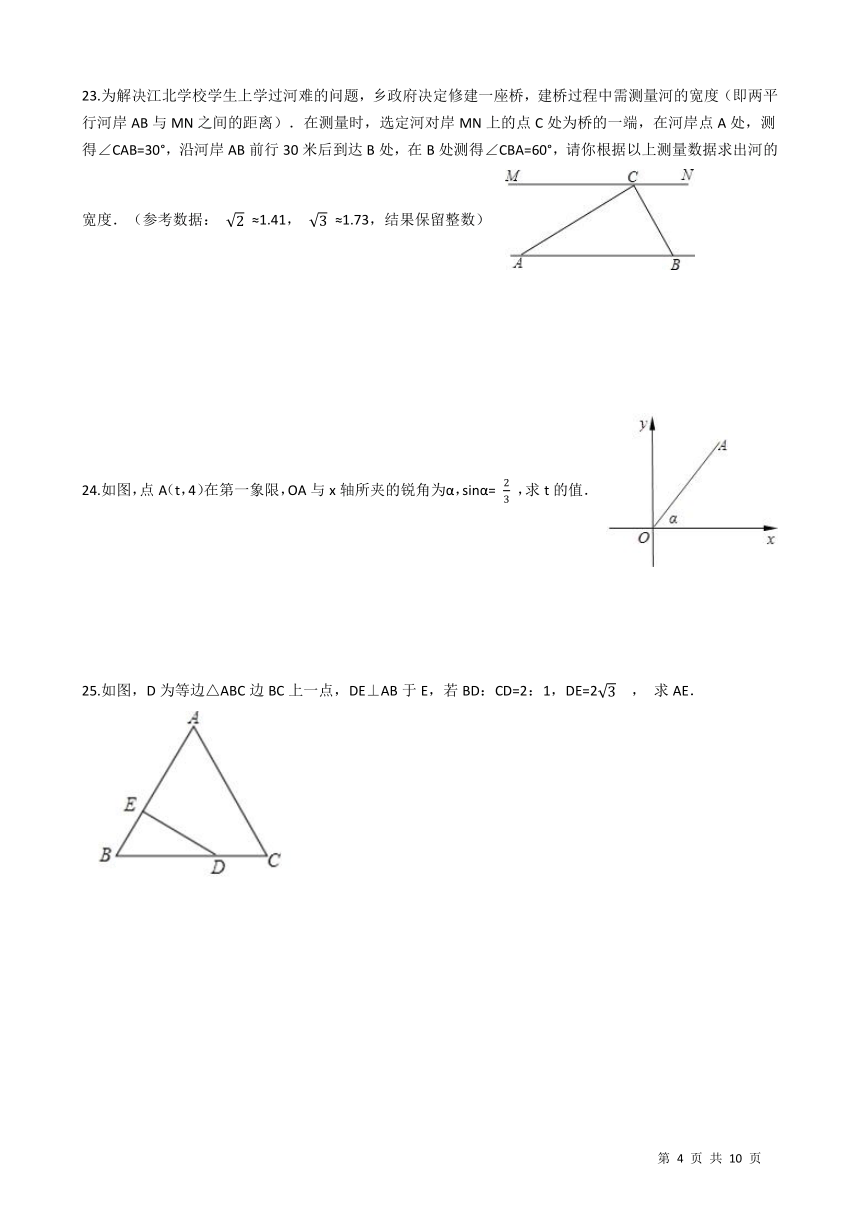
23.为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:
2
≈1.41,
3
≈1.73,结果保留整数) /
24.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα=
2
3
,求t的值. /
25.如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2
3
, 求AE. /
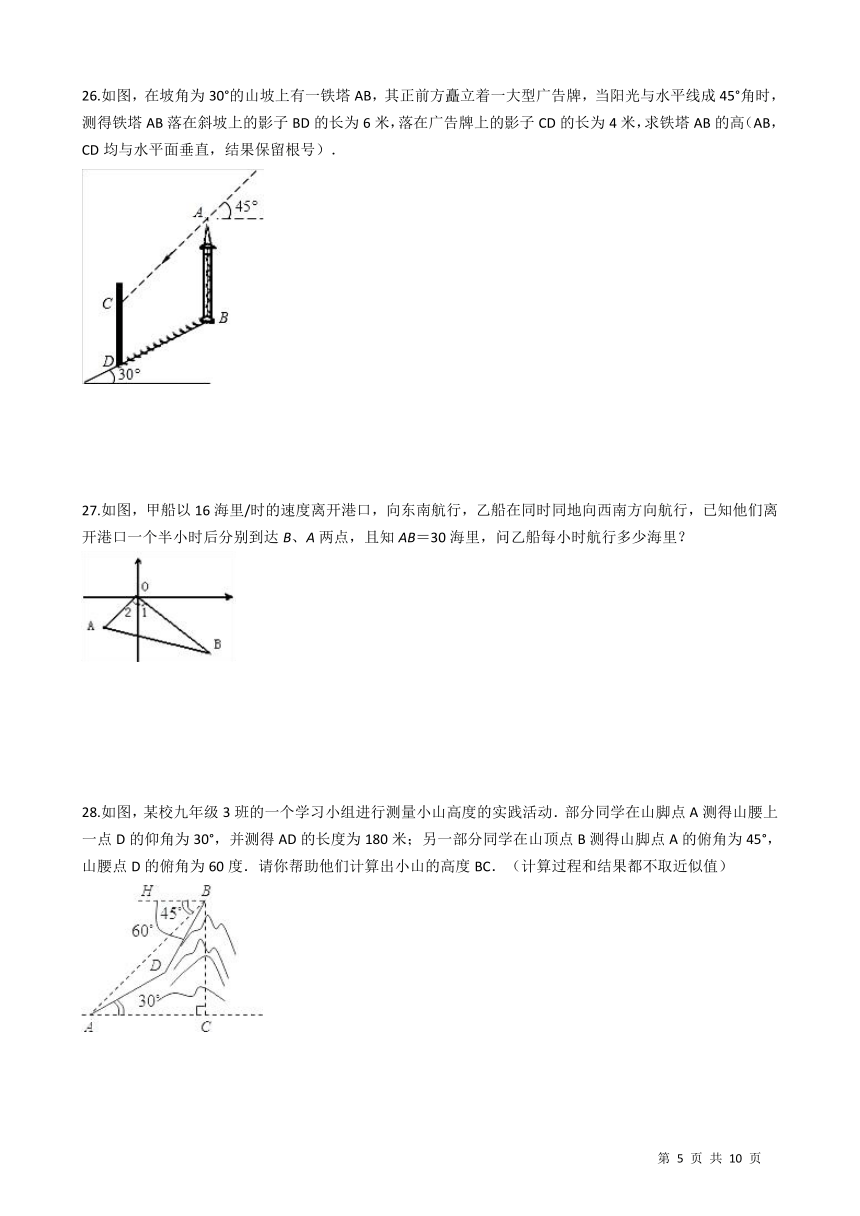
26.如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号). /
27.如图,甲船以16海里/时的速度离开港口,向东南航行,乙船在同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B、A两点,且知AB=30海里,问乙船每小时航行多少海里? /
28.如图,某校九年级3班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60度.请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值) /
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】A
10.【答案】A
二、填空题
11.【答案】
3
4
12.【答案】60
13.【答案】40°
14.【答案】2
15.【答案】
7
5
16.【答案】240
17.【答案】
2
5
5
18.【答案】6或10
19.【答案】16
20.【答案】
6
5
;
44
15
三、解答题
21.【答案】解:原式=2×
1
2
+(-1)+3-1 ???????????? =1-1+3-1 ???????????? =2
22.【答案】解: 过点C作 ????⊥???? 于点D / 由题意得 ∠??=∠??????=30° , ∠??=∠??????=45° ∵在Rt△ACD中, sin??=
????
????
, cos??=
????
????
∴CD=AC sin?? = 400sin30° =400×
1
2
=200(m)? AD= AC cos?? = 400cos30° =400×
3
2
=200
3
(m) ∵在Rt△BCD中, tanB=
????
????
∴BD=
????
tan??
=
200
tan45°
=200 (m) ∴AB=AD+BD= (200
3
+200) m 答:地面上A,B两点间的距离为 (200
3
+200) m .
23.【答案】解:如图,过点C作CD⊥AB于点D, / 设CD=x. ∵在直角△ACD中,∠CAD=30°, ∴AD= /= /x. 同理,在直角△BCD中,BD= /= /x. 又∵AB=30米, ∴AD+BD=30米,即 /x+ /x=30. 解得x=13. 答:河的宽度的13米.
24.【答案】解:过A作AB⊥x轴于B. / ∴ /, ∵ /, ∴ /, ∵A(t,4), ∴AB=4, ∴OA=6, ∴ /.
25.【答案】解:∵△ABC是等边三角形, ∴AB=BC,∠B=60°, ∵DE⊥AB于E, ∴∠DEB=90°, ∴∠BDE=30°, ∴BD=2BE, 在Rt△BDE中,设BE=x,则BD=2x, ∵DE=2
3
, 由勾股定理得:(2x)2﹣x2=(2
3
)2 , 解得:x=2, 所以BE=2,BD=4, ∵BD:CD=2:1, ∴CD=2, ∴BC=BD+CD=6, ∵AB=BC, ∴AB=6, ∵AE=AB﹣BE ∴AE=6﹣2=4.
26.【答案】解:过点C作CE⊥AB于E,过点B作BF⊥CD于F, / 在Rt△BFD中, ∵∠DBF=30°,sin∠DBF=
????
????
=
1
2
,cos∠DBF=
????
????
=
3
2
, ∵BD=6, ∴DF=3,BF=3
3
, ∵AB∥CD,CE⊥AB,BF⊥CD, ∴四边形BFCE为矩形, ∴BF=CE=3
3
,CF=BE=CD﹣DF=1, 在Rt△ACE中,∠ACE=45°, ∴AE=CE=3
3
, ∴AB=3
3
+1. 答:铁塔AB的高为(3
3
+1)m.
27.【答案】解:∵OB=16×1.5=24,AB=30,∠AOB=90°, ∴OA=18, ∴18÷1.5=12(海里/时), 答:乙船每小时航行12 海里
28.【答案】解:如图,过点D作DE⊥AC于点E,作DF⊥BC于点F, 则有DE∥FC,DF∥EC. ∵∠DEC=90°, ∴四边形DECF是矩形, ∴DE=FC. ∵∠HBA=∠BAC=45°, ∴∠BAD=∠BAC﹣∠DAE=45°﹣30°=15度. 又∵∠ABD=∠HBD﹣∠HBA=60°﹣45°=15°, ∴△ADB是等腰三角形.∴AD=BD=180(米). 在Rt△AED中,sin∠DAE=sin30°=
????
????
, ∴DE=180?sin30°=180×
1
2
=90(米),∴FC=90米. 在Rt△BDF中,∠BDF=∠HBD=60°,sin∠BDF=sin60°=
????
????
, ∴BF=180?sin60°=180×
3
2
=90
3
(米). ∴BC=BF+FC=90
3
+90=90(
3
+1)(米). 答:小山的高度BC为90(
3
+1)米. /
一、单选题(共10题;共30分)
1.把三角形三边的长度都扩大为原来的2倍,则锐角A的正弦函数值(????)
A.?扩大为原来的2倍??????????????????????/B.?缩小为原来的
1
2
??????????????????????/C.?不变??????????????????????/D.?不能确定
2.在△ABC中,∠C=90°,sinA=
3
2
,则cosB的值为(??? )
A.?1????????????????????????????????????????/B.?
3
2
????????????????????????????????????????/C.?
2
2
????????????????????????????????????????/D.?
1
2
3.△ABC中,∠C=90°,BC=12,AB=13,那么sinA的值等于(????)
A.?
5
13
???????????????????????????????????????/B.?
12
13
???????????????????????????????????????/C.?
5
12
???????????????????????????????????????/D.?
12
5
4.(2016?陕西)已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为(? )
A.?
1
2
????????????????????????????????????????/B.?
5
5
????????????????????????????????????????/C.?
2
5
5
????????????????????????????????????????/D.?2
5.如图,小明要测量河内小岛 B 到河边公路 l 的距离,在 A 点测得∠BAD=30°,在 C 点测得∠BCD=60°,又测得 AC=60米,则小岛 B 到公路 l 的距离为( ) /
A.?30 米?????????????????????????/B.?30
3
米?????????????????????????/C.?40
3
米?????????????????????????/D.?(30+
3
)米
6.Rt△ABC中,∠C=90°,AB=13,AC=5,则sinB的值为( )
A.?
5
13
???/B.?
13
5
?/C.?
12
13
?/D.?
5
12
7.若α是锐角,tanα?tan50°=1,则α的值为(?? )
A.?20°???????????????????????????????????????B.?30°???????????????????????????????????????C.?40°???????????????????????????????????????D.?50°
8.如图,以O为圆心,任意长为半径画弧,与射线OA交于点B,再以B为圆心,BO长为半径画弧,两弧交于点C,画射线OC,则sin∠AOC的值为(?? ) /
A.?
1
2
???????????????????????????????????????/B.?
3
3
???????????????????????????????????????/C.?
2
2
???????????????????????????????????????/D.?
3
2
9.如图,某侦察机在空中A处发现敌方地面目标B,此时从飞机上看目标B的俯角为α,已知飞行高度AC=4500米,tanα=
5
6
, 则飞机到目标B的水平距离BC为( ) /
A.?5400
5
米????????????????????????/B.?5400
3
米????????????????????????/C.?5600
5
米????????????????????????/D.?5600
3
米
10.(2017?绵阳)如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2
3
,∠AEO=120°,则FC的长度为(?? ) /
A.?1?????????????????????????????????????????/B.?2?????????????????????????????????????????/C.?
2
?????????????????????????????????????????/D.?
3
二、填空题(共10题;共30分)
11.在△ABC中,∠C=90°,sinA= /,则tanB=________.
12.如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为________米.( sin56°≈0.8 , tan56°≈1.5 ) /
13.已知 ?? 为锐角,且 tan
???
10
°
=
3
3
,则锐角 ?? 的度数是________.
14.在菱形ABCD中,DE⊥AB,cosA=
3
5
,BE=2,则tan∠DBE的值是________. /
15.已知α是锐角且tanα=
3
4
, 则sinα+cosα=________?
16.如图,某公园入口处原有三级台阶,每级台阶高为20cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡的坡度i=1:5,则AC的长度是________cm. /
17.在以O为坐标原点的直角坐标平面内有一点A(2,4),如果AO与x轴正半轴的夹角为α,那么sinα=________ .
18.在△ABC中,AB=AC=10,cosB=
3
5
,如果圆O的半径为2
10
,且经过点B、C,那么线段AO的长等于________.
19.如果一个四边形的某个顶点到其他三个顶点的距离相等,我们把这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.如图,已知梯形ABCD是等距四边形,AB//CD,点B是等距点. 若BC=10, cos??=
10
10
,则CD的长等于________. /
20.如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F。若tanA=
1
2
,则
????
????
=________。如图 2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F。若
????
????
=
1
3
,tanA=
1
2
,则
????
????
=________。 //
三、解答题(共8题;共60分)
21.(2017·金华)(本题6分)计算:2cos60°+(?1)2017+|?3|?(2?1)0.
22.如图,从热气球C处测得地面A,B两点的俯角分别为 30° , 45° ,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离. /
23.为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:
2
≈1.41,
3
≈1.73,结果保留整数) /
24.如图,点A(t,4)在第一象限,OA与x轴所夹的锐角为α,sinα=
2
3
,求t的值. /
25.如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2
3
, 求AE. /
26.如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号). /
27.如图,甲船以16海里/时的速度离开港口,向东南航行,乙船在同时同地向西南方向航行,已知他们离开港口一个半小时后分别到达B、A两点,且知AB=30海里,问乙船每小时航行多少海里? /
28.如图,某校九年级3班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60度.请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值) /
答案解析部分
一、单选题
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】A
10.【答案】A
二、填空题
11.【答案】
3
4
12.【答案】60
13.【答案】40°
14.【答案】2
15.【答案】
7
5
16.【答案】240
17.【答案】
2
5
5
18.【答案】6或10
19.【答案】16
20.【答案】
6
5
;
44
15
三、解答题
21.【答案】解:原式=2×
1
2
+(-1)+3-1 ???????????? =1-1+3-1 ???????????? =2
22.【答案】解: 过点C作 ????⊥???? 于点D / 由题意得 ∠??=∠??????=30° , ∠??=∠??????=45° ∵在Rt△ACD中, sin??=
????
????
, cos??=
????
????
∴CD=AC sin?? = 400sin30° =400×
1
2
=200(m)? AD= AC cos?? = 400cos30° =400×
3
2
=200
3
(m) ∵在Rt△BCD中, tanB=
????
????
∴BD=
????
tan??
=
200
tan45°
=200 (m) ∴AB=AD+BD= (200
3
+200) m 答:地面上A,B两点间的距离为 (200
3
+200) m .
23.【答案】解:如图,过点C作CD⊥AB于点D, / 设CD=x. ∵在直角△ACD中,∠CAD=30°, ∴AD= /= /x. 同理,在直角△BCD中,BD= /= /x. 又∵AB=30米, ∴AD+BD=30米,即 /x+ /x=30. 解得x=13. 答:河的宽度的13米.
24.【答案】解:过A作AB⊥x轴于B. / ∴ /, ∵ /, ∴ /, ∵A(t,4), ∴AB=4, ∴OA=6, ∴ /.
25.【答案】解:∵△ABC是等边三角形, ∴AB=BC,∠B=60°, ∵DE⊥AB于E, ∴∠DEB=90°, ∴∠BDE=30°, ∴BD=2BE, 在Rt△BDE中,设BE=x,则BD=2x, ∵DE=2
3
, 由勾股定理得:(2x)2﹣x2=(2
3
)2 , 解得:x=2, 所以BE=2,BD=4, ∵BD:CD=2:1, ∴CD=2, ∴BC=BD+CD=6, ∵AB=BC, ∴AB=6, ∵AE=AB﹣BE ∴AE=6﹣2=4.
26.【答案】解:过点C作CE⊥AB于E,过点B作BF⊥CD于F, / 在Rt△BFD中, ∵∠DBF=30°,sin∠DBF=
????
????
=
1
2
,cos∠DBF=
????
????
=
3
2
, ∵BD=6, ∴DF=3,BF=3
3
, ∵AB∥CD,CE⊥AB,BF⊥CD, ∴四边形BFCE为矩形, ∴BF=CE=3
3
,CF=BE=CD﹣DF=1, 在Rt△ACE中,∠ACE=45°, ∴AE=CE=3
3
, ∴AB=3
3
+1. 答:铁塔AB的高为(3
3
+1)m.
27.【答案】解:∵OB=16×1.5=24,AB=30,∠AOB=90°, ∴OA=18, ∴18÷1.5=12(海里/时), 答:乙船每小时航行12 海里
28.【答案】解:如图,过点D作DE⊥AC于点E,作DF⊥BC于点F, 则有DE∥FC,DF∥EC. ∵∠DEC=90°, ∴四边形DECF是矩形, ∴DE=FC. ∵∠HBA=∠BAC=45°, ∴∠BAD=∠BAC﹣∠DAE=45°﹣30°=15度. 又∵∠ABD=∠HBD﹣∠HBA=60°﹣45°=15°, ∴△ADB是等腰三角形.∴AD=BD=180(米). 在Rt△AED中,sin∠DAE=sin30°=
????
????
, ∴DE=180?sin30°=180×
1
2
=90(米),∴FC=90米. 在Rt△BDF中,∠BDF=∠HBD=60°,sin∠BDF=sin60°=
????
????
, ∴BF=180?sin60°=180×
3
2
=90
3
(米). ∴BC=BF+FC=90
3
+90=90(
3
+1)(米). 答:小山的高度BC为90(
3
+1)米. /
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
