北师大版九年级数学下册期末专题复习第三章圆单元评估检测试卷(有答案)
文档属性
| 名称 | 北师大版九年级数学下册期末专题复习第三章圆单元评估检测试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 184.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-29 23:16:00 | ||
图片预览



文档简介
期末专题复习:北师大版九年级数学下册 第三章 圆 单元评估检测
一、单选题(共10题;共30分)
1.一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为(?? )
A.?6厘米??????????????????????????????/B.?12厘米??????????????????????????????/C.?2
3
厘米??????????????????????????????/D.?
6
厘米
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是( ????) /
A.?∠A﹦∠D???????????????????????????/B.?CE﹦DE???????????????????????????/C.?∠ACB﹦90°???????????????????????????/D.?CE﹦BD
3.如图,平面上⊙O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是(?? ) /
A.?Ll??????????????????????????????????????????B.?L2??????????????????????????????????????????C.?L3??????????????????????????????????????????D.?L4
4.O是△ABC的外心,且∠ABC+∠ACB=100°,则∠BOC=(????? )
A.?100°????????????????????????????????????/B.?120°????????????????????????????????????/C.?130°????????????????????????????????????/D.?160°
5.如图, ???? 是 ⊙?? 直径, ???? 是 ⊙?? 的切线,连接 ???? 交 ⊙?? 于点 ?? ,连接 ???? , ∠??=42° ,则 ∠?????? 的度数是( ??).
/
A.48° B.28° C.34° D.24°
6.若两个圆的周长比为3:7,则它们的面积比为( )
A.?3:7??????????????????????????????????????B.?
3
:
7
??????????????????????????????C.?9:49?????????????????????????????????D.?7:3
7.如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是(?? ) /
A.?△CBE??????????????????????????????????/B.?△ACD??????????????????????????????????/C.?△ABE??????????????????????????????????/D.?△ACE
8.下列命题中是真命题的有( ) ①两个端点能够重合的弧是等弧;②圆的任意一条弦把圆分成优弧和劣弧两部分;③长度相等的弧是等弧;④半径相等的圆是等圆;⑤直径是最大的弦; ⑥半圆所对的弦是直径.
A.?3个???????????????????????????????????????/B.?4个??????????????????????????????????????/C.?5个??????????????????????????????????????/D.?6个
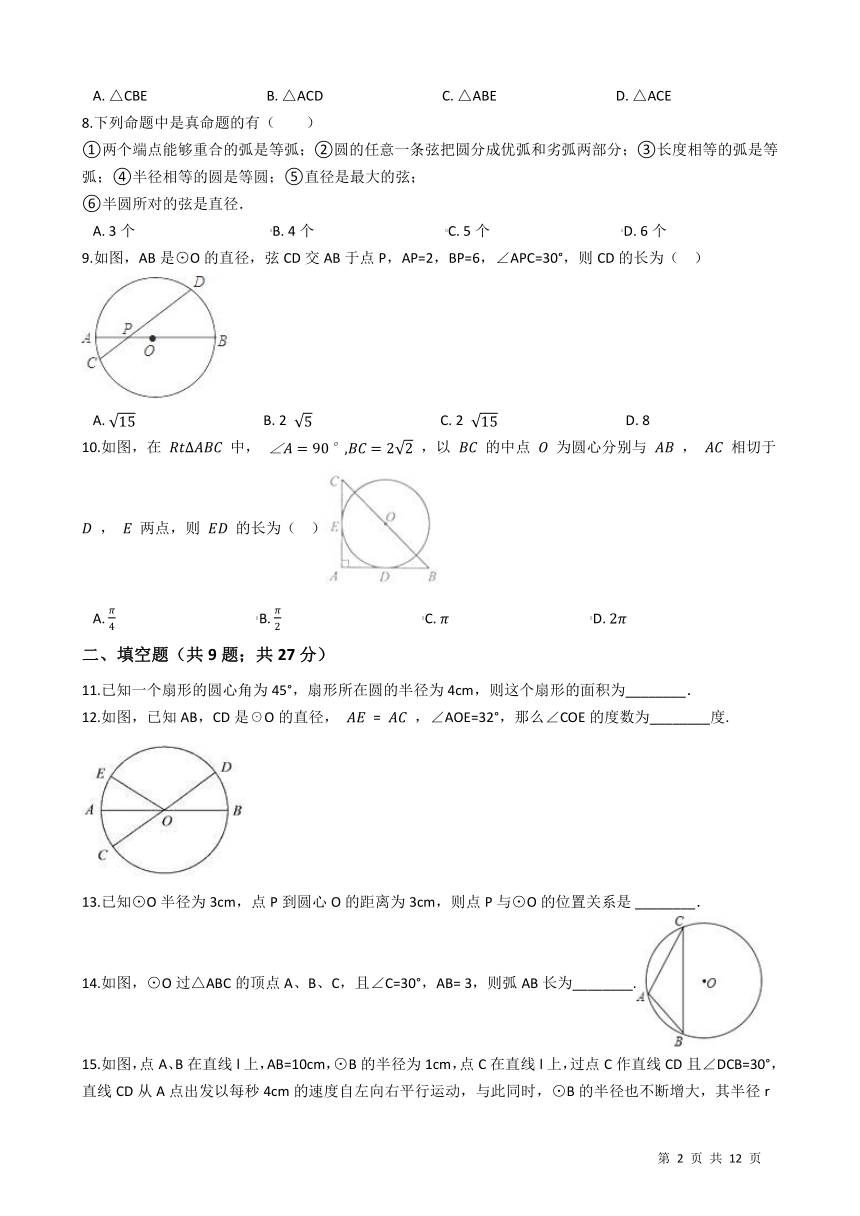
9.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为(?? ) /
A.?
15
?????????????????????????????????????/B.?2
5
?????????????????????????????????????/C.?2
15
?????????????????????????????????????/D.?8
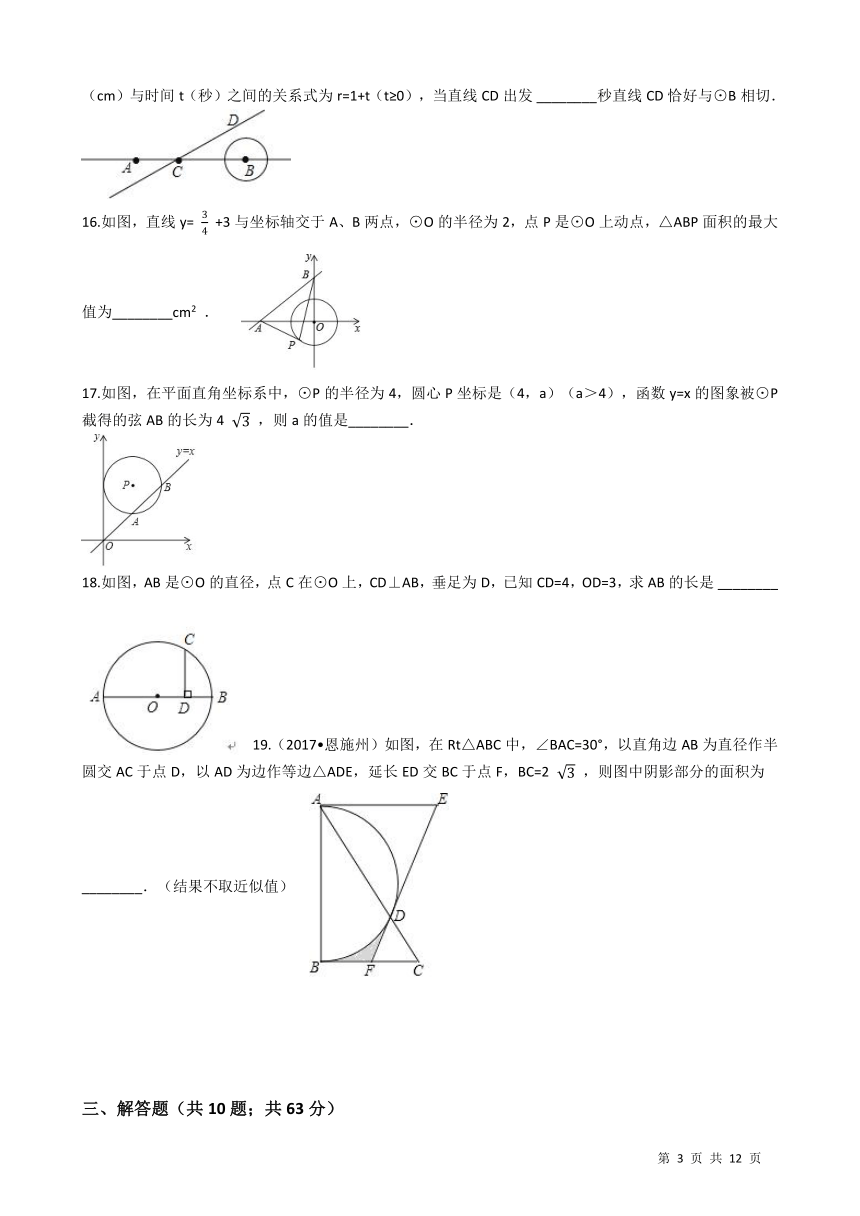
10.如图,在 ???????????? 中, ∠??=90°,????=2
2
,以 ???? 的中点 ?? 为圆心分别与 ???? , ???? 相切于 ?? , ?? 两点,则
????
的长为(?? )/
A.?
??
4
?????????????????????????????????????????/B.?
??
2
?????????????????????????????????????????/C.????????????????????????????????????????????/D.?2??
二、填空题(共9题;共27分)
11.已知一个扇形的圆心角为45°,扇形所在圆的半径为4cm,则这个扇形的面积为________.
12.如图,已知AB,CD是☉O的直径,
????
=
????
,∠AOE=32°,那么∠COE的度数为________度.
/
13.已知⊙O半径为3cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是?________.
14.如图,⊙O过△ABC的顶点A、B、C,且∠C=30°,AB= 3,则弧AB长为________./
15.如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发?________秒直线CD恰好与⊙B相切. /
16.如图,直线y=
3
4
+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为________cm2 . /
17.如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4
3
,则a的值是________. /
18.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是?________
19.(2017?恩施州)如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2
3
,则图中阴影部分的面积为________.(结果不取近似值) /
三、解答题(共10题;共63分)
20.已知:如图,MN、PQ是⊙O的两条弦,且QN=MP, 求证:MN= PQ. /
21.如图,在⊙O中,半径OA⊥OB,∠B=28°,求∠BOC的度数.
/
22.已知抛物线y=x/+bx+c,经过点A(0,5)和点B(3,2) (1)求抛物线的解析式: (2)现有一半径为l,圆心P在抛物线上运动的动圆,问⊙P在运动过程中,是否存在⊙P与坐标轴相切的情况?若存在,请求出圆心P的坐标:若不存在,请说明理由; (3)若⊙Q的半径为r , 点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值
23.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,AC=13,BC=5,弦BD=BA,BE⊥DC交DC的延长线于点E. [MISSING IMAGE: , ] (1)求证:∠BCA=∠BAD; (2)求DE的长.
24.如图,正方形ABCD的外接圆为⊙O,点P在劣弧
????
上(不与C点重合).
/
求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
]25.如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数. /
26.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2
3
. (1)求AC的长度; (2)求图中阴影部分的面积.(计算结果保留根号) /
27.如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F. (1)求证:∠CDB=∠BFD; (2)若AB=10,AC=8,求DF的长. /
28.如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E. (1)求证:BD=ID; (2)求证:ID2=DE?DA. /
29.如图,⊙O的半径均为R. /
(1)请在图①中画出弦AB,CD,使图①为轴对称图形而不是中心对称图形;请在图②中画出弦AB,CD,使图②仍为中心对称图形
(2)如图③,在⊙O中,AB=CD=m(0<m<2R),且AB与CD交于点E,夹角为锐角α.求四边形ACBD的面积(用含m,α的式子表示)
(3)若线段AB,CD是⊙O的两条弦,且AB=CD=
2
R,你认为在以点A,B,C,D为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.
答案解析部分
一、单选题
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】B
二、填空题
11.【答案】2πcm2
12.【答案】64
13.【答案】点P在⊙O上
14.【答案】π
15.【答案】
4
3
或6
16.【答案】11
17.【答案】4+2
2
18.【答案】10
19.【答案】3
3
﹣
3
2
π
三、解答题
20.【答案】证明:∵QN=MP,∴ 弧QN=弧MP,∴弧MN=弧PQ,∴MN=PQ
21.【答案】解:∵OA⊥OB,
∴∠AOB=90°,
∴∠A=90°﹣∠B=90°﹣28°=62°,
∵OA=OC,
∴∠ACO=∠A=62°,
而∠ACO=∠BOC+∠B,
∴∠BOC=62°﹣28°=34°.
22.【答案】解:(1)将A(0,5)和点B(3,2)代入方程??=
??
2
+????+??
2=
3
2
+??×3+??
5=
0
2
+??×0+??
解得:c=5,b=-4 /抛物线的解析式为:??=
??
2
?4??+5 (2)??=
??
2
?4??+5=
???2
2
+1 /抛物线的顶点是(2,1),和y轴的交点是(0,5) ⊙P上一点和坐标轴相切就意味着抛物线上的点到坐标轴的距离是⊙P的半径1 即:抛物线上某点的横坐标或纵坐标为±1 当??=1时,
??
2
?4??+5=1,??=2 当??=1时,??=1?4+5=2 当??=?1时,??=1+4+5=10 当??=?1时,方程无解 存在⊙P与坐标轴相切的情况,且相切时圆点的坐标为(2,1)、(1,2)或(-1,10) (3)⊙Q的点Q 在抛物线上,说明⊙Q的横纵坐标符合抛物线的方程 由第二问的说明得:⊙Q与两坐轴都相切,说明⊙Q的横纵坐标都相等 设⊙Q的坐标为(r,r),带入抛物线的方程:r2-4r+5=r ??=
5±
5
2
23.【答案】(1)根据BD=BA得出∠BDA=∠BAD,再由∠BCA=∠BDA即可得出结论; (2)判断△BED∽△CBA,利用对应边成比例的性质可求出DE的长度. 试题解析:(1)∵∠BCA=∠BDA, ∵BD=BA, ∴∠BAD=∠BDA, ∴∠BCA=∠BAD. (2)在Rt/ABC中,∠ABC=90°,AC=13,BC=5, ∴/, ∵BE⊥DC,∴∠E=90°, ∵∠EDB=∠BAC. ∴△DEB∽△ABC, ∴/, ∴/.
24.【答案】(1)解:连接OB,OC,/∵四边形ABCD为正方形,∴∠BOC=90°,∴∠BPC=
1
2
∠BOC=45°; (2)解:过点O作OE⊥BC于点E, ∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,∵OE2+BE2=OB2 , ∴BE=
??
??
2
2
=
32
=4
2
?∴BC=2BE=2× 4
2
=8
2
25.【答案】解:∵AB为⊙O直径 ∴∠ADB=90° ∵相同的弧所对应的圆周角相等,且∠ACD=25° ∴∠B=25° ∴∠BAD=90°﹣∠B=65°
26.【答案】解:(1)∵OF⊥AB, ∴∠BOF=90°, ∵∠B=30°,FO=2
3
, ∴OB=6,AB=2OB=12, 又∵AB为⊙O的直径, ∴∠ACB=90°, ∴AC=
1
2
AB=6; (2)∵由(1)可知,AB=12, ∴AO=6,即AC=AO, 在Rt△ACF和Rt△AOF中,
????=????
????=????
∴Rt△ACF≌Rt△AOF, ∴∠FAO=∠FAC=30°, ∴∠DOB=60°, 过点D作DG⊥AB于点G, / ∵OD=6,∴DG=3
3
, ∴S△ACF+S△OFD=S△AOD=
1
2
×6×3
3
=9
3
, 即阴影部分的面积是9
3
.
27.【答案】解:(1)∵DF与⊙O相切, ∴DF⊥OD, ∵OD⊥AC, ∴DF∥AC, ∴∠CAB=∠BFD, ∴∠CAB=∠BFD, ∴∠CDB=∠BFD; (2)∵半径OD垂直于弦AC于点E,AC=8, ∴AE=
1
2
AC=
1
2
×8=4. ∵AB是⊙O的直径, ∴OA=OD=
1
2
AB=
1
2
×10=5, 在Rt△AEO中,OE=
??
??
2
???
??
2
=
5
2
?
4
2
=3, ∵AC∥DF, ∴△OAE∽△OFD. ∴
????
????
=
????
????
, ∴
3
5
=
4
????
, ∴DF=
20
3
.
28.【答案】(2)证明:连接BI,CI,CD, ∵I为内心, ∴AI为∠BAC角平分线, BI为∠ABC平分线, ∴∠ABI=∠CBI,∠BAD=∠DAC, ∵∠BID=∠ABI+∠BAI, ∠CBD=∠DAC=∠BAI, ∴∠BID=∠CBI+∠CBD=∠DBI, ∴△DBI为等腰三角形, ∴DB=DI; (3)证明:∵∠DBE=∠CAD,∠BAE=∠CAE, ∴∠BAE=∠EBD, ∴△DBE∽△DAB, ∴
????
????
=
????
????
, ∴DB2=DE?DA, 又∵DB=DI(已证), ∴DI2=DE?DA. /
29.【答案】(1)解:答案不唯一,如图①、② / (2)解: 过点A,B分别作CD的垂线,垂足分别为M,N, ∵S△ACD=
1
2
CD?AM=
1
2
CD?AE?sinα,S△BCD=
1
2
CD?BN=
1
2
CD?BE?sinα, ∴S四边形ACBD=S△ACD+S△BCD=
1
2
CD?AE?sinα+
1
2
CD?BE?sinα =
1
2
CD?(AE+BE)sinα=
1
2
CD?AB?sinα=
1
2
m2?sinα. (3)解: 存在.分两种情况说明如下: ①当AB与CD相交时,由(2)及AB=CD=
2
R知S四边形ACBD=
1
2
AB?CD?sinα=R2sinα, ②当AB与CD不相交时,如图④. /? ∵AB=CD=
2
R , OC=OD=OA=OB=R, ∴∠AOB=∠COD=90°. 而S四边形ABCD=SRt△AOB+SRt△OCD+S△AOD+S△BOC=R2+S△AOD+S△BOC 延长BO交⊙O于点E,连接EC, 则∠1+∠3=∠2+∠3=90°. ∴∠1=∠2. ∴△AOD≌△COE. ∴S△AOD=S△OCE ∴S△AOD+S△BOC=S△OCE+S△BOC=S△BCE 过点C作CH⊥BE,垂足为H, 则S△BCE=
1
2
BE?CH=R?CH. ∴当CH=R时,S△BCE取最大值R2 综合①、②可知,当∠1=∠2=90°. 即四边形ABCD是边长为
2
R的正方形时,S四边形ABCD=R2+R2=2R2为最大值.
一、单选题(共10题;共30分)
1.一个扇形的圆心角为60°,弧长为2π厘米,则这个扇形的半径为(?? )
A.?6厘米??????????????????????????????/B.?12厘米??????????????????????????????/C.?2
3
厘米??????????????????????????????/D.?
6
厘米
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中不成立的是( ????) /
A.?∠A﹦∠D???????????????????????????/B.?CE﹦DE???????????????????????????/C.?∠ACB﹦90°???????????????????????????/D.?CE﹦BD
3.如图,平面上⊙O与四条直线L1、L2、L3、L4的位置关系.若⊙O的半径为2cm,且O点到其中一条直线的距离为2.2cm,则这条直线是(?? ) /
A.?Ll??????????????????????????????????????????B.?L2??????????????????????????????????????????C.?L3??????????????????????????????????????????D.?L4
4.O是△ABC的外心,且∠ABC+∠ACB=100°,则∠BOC=(????? )
A.?100°????????????????????????????????????/B.?120°????????????????????????????????????/C.?130°????????????????????????????????????/D.?160°
5.如图, ???? 是 ⊙?? 直径, ???? 是 ⊙?? 的切线,连接 ???? 交 ⊙?? 于点 ?? ,连接 ???? , ∠??=42° ,则 ∠?????? 的度数是( ??).
/
A.48° B.28° C.34° D.24°
6.若两个圆的周长比为3:7,则它们的面积比为( )
A.?3:7??????????????????????????????????????B.?
3
:
7
??????????????????????????????C.?9:49?????????????????????????????????D.?7:3
7.如图,点O为等边三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,下列三角形中,外心不是点O的是(?? ) /
A.?△CBE??????????????????????????????????/B.?△ACD??????????????????????????????????/C.?△ABE??????????????????????????????????/D.?△ACE
8.下列命题中是真命题的有( ) ①两个端点能够重合的弧是等弧;②圆的任意一条弦把圆分成优弧和劣弧两部分;③长度相等的弧是等弧;④半径相等的圆是等圆;⑤直径是最大的弦; ⑥半圆所对的弦是直径.
A.?3个???????????????????????????????????????/B.?4个??????????????????????????????????????/C.?5个??????????????????????????????????????/D.?6个
9.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为(?? ) /
A.?
15
?????????????????????????????????????/B.?2
5
?????????????????????????????????????/C.?2
15
?????????????????????????????????????/D.?8
10.如图,在 ???????????? 中, ∠??=90°,????=2
2
,以 ???? 的中点 ?? 为圆心分别与 ???? , ???? 相切于 ?? , ?? 两点,则
????
的长为(?? )/
A.?
??
4
?????????????????????????????????????????/B.?
??
2
?????????????????????????????????????????/C.????????????????????????????????????????????/D.?2??
二、填空题(共9题;共27分)
11.已知一个扇形的圆心角为45°,扇形所在圆的半径为4cm,则这个扇形的面积为________.
12.如图,已知AB,CD是☉O的直径,
????
=
????
,∠AOE=32°,那么∠COE的度数为________度.
/
13.已知⊙O半径为3cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是?________.
14.如图,⊙O过△ABC的顶点A、B、C,且∠C=30°,AB= 3,则弧AB长为________./
15.如图,点A、B在直线l上,AB=10cm,⊙B的半径为1cm,点C在直线l上,过点C作直线CD且∠DCB=30°,直线CD从A点出发以每秒4cm的速度自左向右平行运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0),当直线CD出发?________秒直线CD恰好与⊙B相切. /
16.如图,直线y=
3
4
+3与坐标轴交于A、B两点,⊙O的半径为2,点P是⊙O上动点,△ABP面积的最大值为________cm2 . /
17.如图,在平面直角坐标系中,⊙P的半径为4,圆心P坐标是(4,a)(a>4),函数y=x的图象被⊙P截得的弦AB的长为4
3
,则a的值是________. /
18.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是?________
19.(2017?恩施州)如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=2
3
,则图中阴影部分的面积为________.(结果不取近似值) /
三、解答题(共10题;共63分)
20.已知:如图,MN、PQ是⊙O的两条弦,且QN=MP, 求证:MN= PQ. /
21.如图,在⊙O中,半径OA⊥OB,∠B=28°,求∠BOC的度数.
/
22.已知抛物线y=x/+bx+c,经过点A(0,5)和点B(3,2) (1)求抛物线的解析式: (2)现有一半径为l,圆心P在抛物线上运动的动圆,问⊙P在运动过程中,是否存在⊙P与坐标轴相切的情况?若存在,请求出圆心P的坐标:若不存在,请说明理由; (3)若⊙Q的半径为r , 点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值
23.如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,AC=13,BC=5,弦BD=BA,BE⊥DC交DC的延长线于点E. [MISSING IMAGE: , ] (1)求证:∠BCA=∠BAD; (2)求DE的长.
24.如图,正方形ABCD的外接圆为⊙O,点P在劣弧
????
上(不与C点重合).
/
求∠BPC的度数;
(2)若⊙O的半径为8,求正方形ABCD的边长.
]25.如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数. /
26.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=2
3
. (1)求AC的长度; (2)求图中阴影部分的面积.(计算结果保留根号) /
27.如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F. (1)求证:∠CDB=∠BFD; (2)若AB=10,AC=8,求DF的长. /
28.如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E. (1)求证:BD=ID; (2)求证:ID2=DE?DA. /
29.如图,⊙O的半径均为R. /
(1)请在图①中画出弦AB,CD,使图①为轴对称图形而不是中心对称图形;请在图②中画出弦AB,CD,使图②仍为中心对称图形
(2)如图③,在⊙O中,AB=CD=m(0<m<2R),且AB与CD交于点E,夹角为锐角α.求四边形ACBD的面积(用含m,α的式子表示)
(3)若线段AB,CD是⊙O的两条弦,且AB=CD=
2
R,你认为在以点A,B,C,D为顶点的四边形中,是否存在面积最大的四边形?请利用图④说明理由.
答案解析部分
一、单选题
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】A
9.【答案】C
10.【答案】B
二、填空题
11.【答案】2πcm2
12.【答案】64
13.【答案】点P在⊙O上
14.【答案】π
15.【答案】
4
3
或6
16.【答案】11
17.【答案】4+2
2
18.【答案】10
19.【答案】3
3
﹣
3
2
π
三、解答题
20.【答案】证明:∵QN=MP,∴ 弧QN=弧MP,∴弧MN=弧PQ,∴MN=PQ
21.【答案】解:∵OA⊥OB,
∴∠AOB=90°,
∴∠A=90°﹣∠B=90°﹣28°=62°,
∵OA=OC,
∴∠ACO=∠A=62°,
而∠ACO=∠BOC+∠B,
∴∠BOC=62°﹣28°=34°.
22.【答案】解:(1)将A(0,5)和点B(3,2)代入方程??=
??
2
+????+??
2=
3
2
+??×3+??
5=
0
2
+??×0+??
解得:c=5,b=-4 /抛物线的解析式为:??=
??
2
?4??+5 (2)??=
??
2
?4??+5=
???2
2
+1 /抛物线的顶点是(2,1),和y轴的交点是(0,5) ⊙P上一点和坐标轴相切就意味着抛物线上的点到坐标轴的距离是⊙P的半径1 即:抛物线上某点的横坐标或纵坐标为±1 当??=1时,
??
2
?4??+5=1,??=2 当??=1时,??=1?4+5=2 当??=?1时,??=1+4+5=10 当??=?1时,方程无解 存在⊙P与坐标轴相切的情况,且相切时圆点的坐标为(2,1)、(1,2)或(-1,10) (3)⊙Q的点Q 在抛物线上,说明⊙Q的横纵坐标符合抛物线的方程 由第二问的说明得:⊙Q与两坐轴都相切,说明⊙Q的横纵坐标都相等 设⊙Q的坐标为(r,r),带入抛物线的方程:r2-4r+5=r ??=
5±
5
2
23.【答案】(1)根据BD=BA得出∠BDA=∠BAD,再由∠BCA=∠BDA即可得出结论; (2)判断△BED∽△CBA,利用对应边成比例的性质可求出DE的长度. 试题解析:(1)∵∠BCA=∠BDA, ∵BD=BA, ∴∠BAD=∠BDA, ∴∠BCA=∠BAD. (2)在Rt/ABC中,∠ABC=90°,AC=13,BC=5, ∴/, ∵BE⊥DC,∴∠E=90°, ∵∠EDB=∠BAC. ∴△DEB∽△ABC, ∴/, ∴/.
24.【答案】(1)解:连接OB,OC,/∵四边形ABCD为正方形,∴∠BOC=90°,∴∠BPC=
1
2
∠BOC=45°; (2)解:过点O作OE⊥BC于点E, ∵OB=OC,∠BOC=90°,∴∠OBE=45°,∴OE=BE,∵OE2+BE2=OB2 , ∴BE=
??
??
2
2
=
32
=4
2
?∴BC=2BE=2× 4
2
=8
2
25.【答案】解:∵AB为⊙O直径 ∴∠ADB=90° ∵相同的弧所对应的圆周角相等,且∠ACD=25° ∴∠B=25° ∴∠BAD=90°﹣∠B=65°
26.【答案】解:(1)∵OF⊥AB, ∴∠BOF=90°, ∵∠B=30°,FO=2
3
, ∴OB=6,AB=2OB=12, 又∵AB为⊙O的直径, ∴∠ACB=90°, ∴AC=
1
2
AB=6; (2)∵由(1)可知,AB=12, ∴AO=6,即AC=AO, 在Rt△ACF和Rt△AOF中,
????=????
????=????
∴Rt△ACF≌Rt△AOF, ∴∠FAO=∠FAC=30°, ∴∠DOB=60°, 过点D作DG⊥AB于点G, / ∵OD=6,∴DG=3
3
, ∴S△ACF+S△OFD=S△AOD=
1
2
×6×3
3
=9
3
, 即阴影部分的面积是9
3
.
27.【答案】解:(1)∵DF与⊙O相切, ∴DF⊥OD, ∵OD⊥AC, ∴DF∥AC, ∴∠CAB=∠BFD, ∴∠CAB=∠BFD, ∴∠CDB=∠BFD; (2)∵半径OD垂直于弦AC于点E,AC=8, ∴AE=
1
2
AC=
1
2
×8=4. ∵AB是⊙O的直径, ∴OA=OD=
1
2
AB=
1
2
×10=5, 在Rt△AEO中,OE=
??
??
2
???
??
2
=
5
2
?
4
2
=3, ∵AC∥DF, ∴△OAE∽△OFD. ∴
????
????
=
????
????
, ∴
3
5
=
4
????
, ∴DF=
20
3
.
28.【答案】(2)证明:连接BI,CI,CD, ∵I为内心, ∴AI为∠BAC角平分线, BI为∠ABC平分线, ∴∠ABI=∠CBI,∠BAD=∠DAC, ∵∠BID=∠ABI+∠BAI, ∠CBD=∠DAC=∠BAI, ∴∠BID=∠CBI+∠CBD=∠DBI, ∴△DBI为等腰三角形, ∴DB=DI; (3)证明:∵∠DBE=∠CAD,∠BAE=∠CAE, ∴∠BAE=∠EBD, ∴△DBE∽△DAB, ∴
????
????
=
????
????
, ∴DB2=DE?DA, 又∵DB=DI(已证), ∴DI2=DE?DA. /
29.【答案】(1)解:答案不唯一,如图①、② / (2)解: 过点A,B分别作CD的垂线,垂足分别为M,N, ∵S△ACD=
1
2
CD?AM=
1
2
CD?AE?sinα,S△BCD=
1
2
CD?BN=
1
2
CD?BE?sinα, ∴S四边形ACBD=S△ACD+S△BCD=
1
2
CD?AE?sinα+
1
2
CD?BE?sinα =
1
2
CD?(AE+BE)sinα=
1
2
CD?AB?sinα=
1
2
m2?sinα. (3)解: 存在.分两种情况说明如下: ①当AB与CD相交时,由(2)及AB=CD=
2
R知S四边形ACBD=
1
2
AB?CD?sinα=R2sinα, ②当AB与CD不相交时,如图④. /? ∵AB=CD=
2
R , OC=OD=OA=OB=R, ∴∠AOB=∠COD=90°. 而S四边形ABCD=SRt△AOB+SRt△OCD+S△AOD+S△BOC=R2+S△AOD+S△BOC 延长BO交⊙O于点E,连接EC, 则∠1+∠3=∠2+∠3=90°. ∴∠1=∠2. ∴△AOD≌△COE. ∴S△AOD=S△OCE ∴S△AOD+S△BOC=S△OCE+S△BOC=S△BCE 过点C作CH⊥BE,垂足为H, 则S△BCE=
1
2
BE?CH=R?CH. ∴当CH=R时,S△BCE取最大值R2 综合①、②可知,当∠1=∠2=90°. 即四边形ABCD是边长为
2
R的正方形时,S四边形ABCD=R2+R2=2R2为最大值.
