上海市杨浦区2019届高三上学期期末质量调研数学试题(小题解析版)
文档属性
| 名称 | 上海市杨浦区2019届高三上学期期末质量调研数学试题(小题解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-30 22:31:46 | ||
图片预览




文档简介
上海市杨浦区2019届高三期末质量调研
数学试卷2018.12
一. 填空题(本大题共12题,1-6每题4分,7-12每题5分,共54分)
1. 设全集,若集合,则
答案:
考点:集合的运算。
解析:全集U中找集合A没有的元素,所以,
2. 已知扇形的半径为6,圆心角为,则扇形的面积为
答案:
考点:弧度制下扇形面积的计算。
解析:扇形的弧长为:,
扇形面积为:S=。
3. 已知双曲线,则其两条渐近线的夹角为
答案:
考点:双曲线的性质。
解析:双曲线的渐近为:,所以,夹角为
4. 若展开式的二项式系数之和为8,则
答案:3
考点:二项式定理。
解析:二项式系数之和为8,所以,=8,故n=3。
5. 若实数、满足,则的取值范围是
答案:
考点:参数方程,三角函数。
解析:由,可令,则,
因为,所以,的范围为:
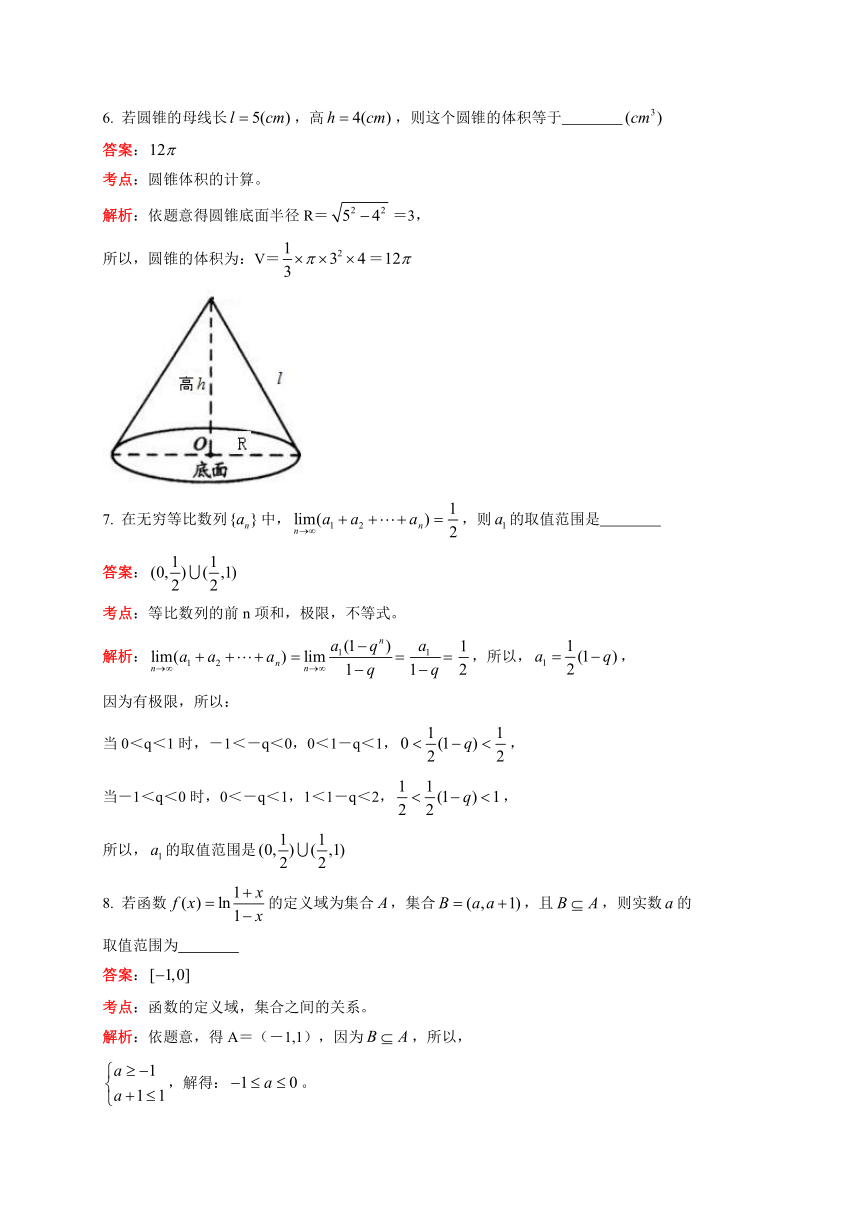
6. 若圆锥的母线长,高,则这个圆锥的体积等于
答案:
考点:圆锥体积的计算。
解析:依题意得圆锥底面半径R==3,
所以,圆锥的体积为:V==
7. 在无穷等比数列中,,则的取值范围是
答案:
考点:等比数列的前n项和,极限,不等式。
解析:,所以,,
因为有极限,所以:
当0<q<1时,-1<-q<0,0<1-q<1,,
当-1<q<0时,0<-q<1,1<1-q<2,,
所以,的取值范围是
8. 若函数的定义域为集合,集合,且,则实数的
取值范围为
答案:
考点:函数的定义域,集合之间的关系。
解析:依题意,得A=(-1,1),因为,所以,
,解得:。
9. 在行列式中,第3行第2列的元素的代数余子式记作,则
的零点是
答案:
考点:矩阵的运算,函数的零点。
解析:依题意,得:=-=
==,解得:,
所以,零点为:
10. 已知复数,(,为虚数单位),在复平面上,设复数、对应的点分别为、,若,其中是坐标原点,则函数的最小正周期为
答案:
考点:复数的几何意义,平面向量,三角恒等变换。
解析:依题意,有:,,
因为,所以,=0,即
=0,化简,得:
==
=,所以,最小正周期为:T=
11. 当时,不等式恒成立,则实数的最大值为
答案:2
考点:基本不等式,不等式恒成立问题。
解析:恒成立,即成立,
,
当,即时,,
所以,,解得:,所以,的最大值为2
12. 设为等差数列的公差,数列的前项和,满足(),
且,若实数(,),则称具有性质,
若是数列的前项和,对任意的,都具有性质,则所有满足条件的
的值为
答案:或4
考点:由数列的前n项和求数列的通项公式,等差数列的通项公式,分类讨论的数学思想。
解析:由,当n=1时,,得:,
当n=3时,,当n=4时,,两式相减得,
又,得:,
所以,,由,得:,
所以,,
又,
当n=2k,时,,则
当n=2k-1,时,,则
所以,,所以,
二. 选择题(本大题共4题,每题5分,共20分)
13. 下列函数中既是奇函数,又在区间上单调递减的是( )
A. B. C. D.
答案:C
考点:函数的奇偶性,单调性。
解析:B、D是偶函数,排除;
又函数是增函数,所以,A也排除;
对于C,既是奇函数,又是减函数,所以,选C。
14. 某象棋俱乐部有队员5人,其中女队员2人,现随机选派2人参加一个象棋比赛,则选出的2人中恰有1人是女队员的概率为( )
A. B. C. D.
答案:B
考点:排列组合,古典概型。
解析:5名队员任派2人,可能为:=10种,
恰有1人是女队员的可能有:=6
所以,所求概率为:P=,选B。
15. 已知,,设,,
,则、、的大小关系是( )
A. B. C. D.
答案:D
考点:三角函数,对数函数,基本不等式。
解析:因为,所以,,所以,在上单调递减,
,所以,,所以,,
所以,≤,即;
,
所以,,即,
所以,
16. 已知函数,记集合,
集合,若,且都不是空集,则的取值范围是( )
A. B. C. D.
答案:A
考点:集合的运算,分类讨论的数学思想。
解析:设A,则,
又A=B,所以,B,即,
所以,,得m=0,从而,
==0,
当n=0时,A=B={0},满足题意;
当n≠0时,由方程=0,得x=0或-n,
而x=0或-n不是方程的根,所以,无解,
即△=,解得:0<n<4,
综上,0≤n<4
所以,的取值范围是
三. 解答题(本大题共5题,共14+14+14+16+18=76分)
17. 如图,PA⊥平面ABCD,四边形ABCD为矩形,,,点F是PB
的中心,点E在边BC上移动.
(1)求三棱锥的体积;
(2)证明:无论点E在边BC的何处,都有AF⊥PE.
18. 在△中,角A、B、C所对的边分别为a、b、c,且.
(1)若,求;
(2)已知,证明:.
19. 上海某工厂以千克/小时的速度匀速生产某种产品,每一小时可获得的利润是
元,其中.
(1)要使生产该产品2小时获得的利润不低于30元,求的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:该厂应选取何种生产速度?并求最大利润.
20. 如图,已知点是轴左侧(不含轴)一点,抛物线上存在不同的两点、
,满足、的中点均在抛物线上.
(1)求抛物线的焦点到准线的距离;
(2)设中点为,且,,证明:;
(3)若是曲线()上的动点,求△PAB面积的最小值.
21. 记无穷数列的前项中最大值为,最小值为,令,.
(1)若,请写出的值;
(2)求证:“数列是等差数列”是“数列是等差数列”的充要条件;
(3)若对任意,有,且,请问:是否存在,使得对于任意不小于的正整数,有成立?请说明理由.
参考答案
一. 填空题
1. 2. 3. 4.
5. 6. 7. 8.
9. 10. 11. 12. 或4
二. 选择题
13. C 14. B 15. D 16. A
三. 解答题
19.答案:(1);(2),最大值为4575.
解析:(1)2(5x+1-)≥30,即5x+1-≥15
整理可得:,解得:x≥3或x≤-(舍去)
所以: 3≤x≤10
(2) 要使生产900千克该产品获得的利润最大时为y,
生产900千克该产品需要时间:t=,
y=×=4500+-=-2700()+4500
=-2700+4575
1≤x≤10,所以当x=6,y取最大值为4575元
20.(1)焦点坐标为(1,0),准线方程为x=-1,所以,焦点到准线的距离为2
(2)设,,,
则中点为,由中点在抛物线上,可得,
化简得,显然,
且对也有,
所以是二次方程的两不等实根,
所以,。
(3),
由(1)可得,,
,
此时在半椭圆上,
∴,
∵,∴,
∴,
,
所以,
,所以,
即的面积的最小值是.
同课章节目录
