陕西省商洛中学2018-2019学年上学期高一第三次月考数学试卷
文档属性
| 名称 | 陕西省商洛中学2018-2019学年上学期高一第三次月考数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 644.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-12-30 23:05:19 | ||
图片预览


文档简介
陕西省商洛中学2018-2019学年上学期高一第三次月考
数学试题
满分:150分 考试时间: 120分钟
注意事项:
1、答第I卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上;
2、每题选出答案后,用2B铅笔把答题卡对应题目的答案涂黑。如需改动,用橡皮擦干净后,再改涂在其它答案标号上;
3、填空题答案写在答题纸规定的题号处;
4、解答题应写出文字说明、推理或演算过程;每题务必在答题纸题号所指示的答题区域作答。
本试卷分第I卷(选择题)和第II卷(非选择题)两部分
第I卷(选择题 共60分)
一、选择题:(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求)
1.如下图所示,观察四个几何体,其中判断正确的是 【 】
A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱
2、经过平面外三点,作与平面平行的平面,则这样的平面可以作 【 】
A. 0个 B. 1个 C. 0个或1个 D. 0个,1个或2个
3、下列命题正确的个数是 【 】
①棱柱的侧面为平行四边形;②正三棱锥也称正四面体;
③以直角三角形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥;
④圆台的任意两条母线的延长线(反向延长线)必交于一点。
A. 0个 B. 1个 C. 2个 D. 3个
4、已知函数 的反函数为,则 【 】
A. B.
C. D.
正方体的体积是64,则其表面积是 【 】
A.64 B.16 C.96 D.无法确定
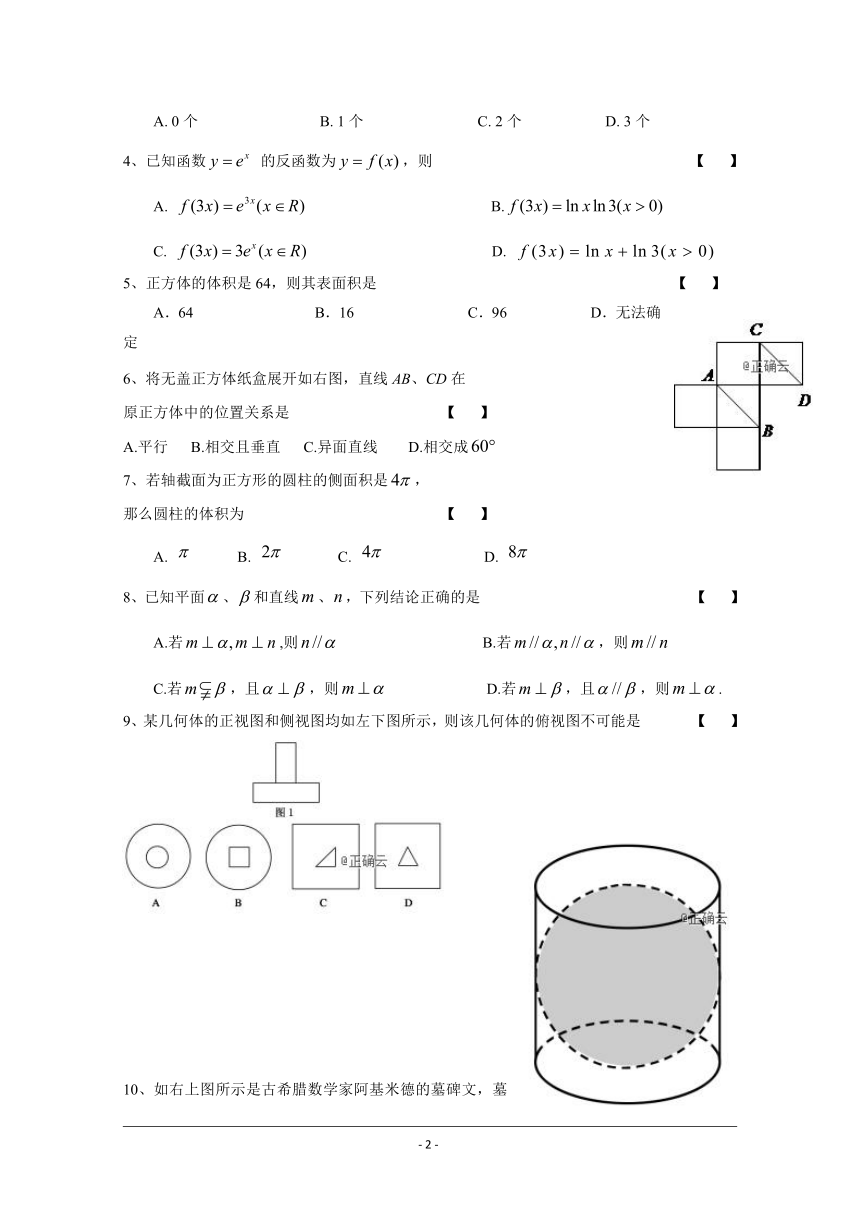
将无盖正方体纸盒展开如右图,直线AB、CD在
原正方体中的位置关系是 【 】
A.平行 B.相交且垂直 C.异面直线 D.相交成
7、若轴截面为正方形的圆柱的侧面积是,
那么圆柱的体积为 【 】
A. B. C. D.
8、已知平面、和直线、,下列结论正确的是 【 】
A.若,则 B.若,则
C.若,且,则 D.若,且,则.
9、某几何体的正视图和侧视图均如左下图所示,则该几何体的俯视图不可能是 【 】
10、如右上图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为 【 】
A .,1 B.,1 C., D.,
11.若定义函数满足,(为常数),则称为等差函数,下列为等差函数的是 【 】
A. B. C. D.
12 .已知矩形将沿矩形的对角线折起,在翻折过程中【 】
A. 存在某个位置,使直线与直线垂直
B. 存在某个位置,使直线与直线垂直
C. 存在某个位置,使直线与直线垂直
D. 三对直线“与”,“与”,“与”始终都不垂直
第Ⅱ卷 (非选择题 共90分)
填空题:(本大题共4小题,每小题5分,满分20分)
13、已知函数,,则实数= .
14、将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的侧面积为 .
15、已知水平放置的△ABC按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么原△ABC的面积是 .
一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为3,则这个球的体积为 .
三、解答题:(本大题共6小题,共70分.解答应写出文字说明、推理过程或演算过程.)
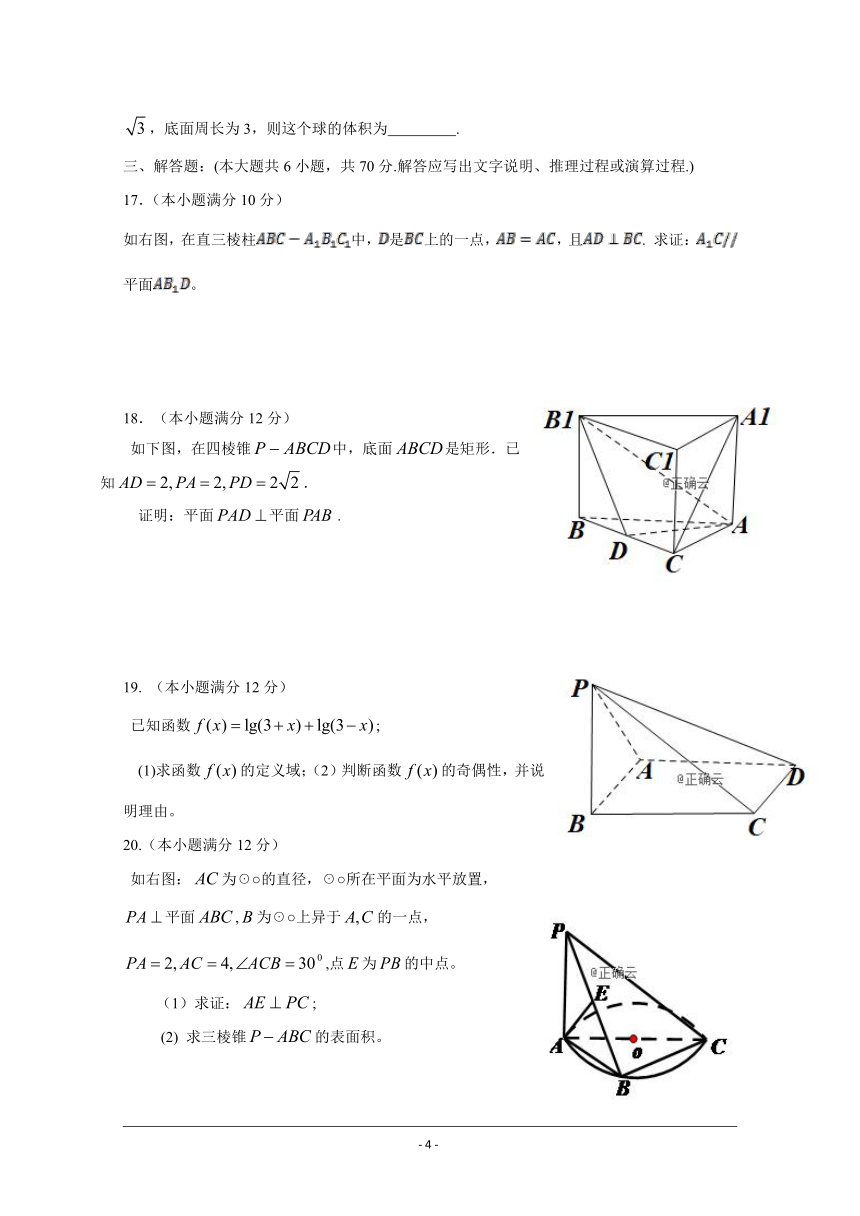
17.(本小题满分10分)
如右图,在直三棱柱中,是上的一点,,且. 求证:平面。
(本小题满分12分)
如下图,在四棱锥中,底面是矩形.已知.
证明:平面平面.
19. (本小题满分12分)
已知函数;
(1)求函数的定义域;(2)判断函数的奇偶性,并说明理由。
20.(本小题满分12分)
如右图:为☉○的直径,☉○所在平面为水平放置,
平面,为☉○上异于的一点,
,点为的中点。
(1)求证:;
(2) 求三棱锥的表面积。
21.(本小题满分12分)
如图4:已知正四棱柱中,底面边长,侧棱的长为4,过点作的垂线交侧棱于点,交于点.
(1)求异面直线与夹角的正切值;
(2)求证:平面;
22.(本小题满分12分)
经开区建造圆锥形仓库用于贮藏粮食,已建的仓库的底面直径为,高为。随着经开区农业经济的发展,粮食产量增大,经开区现拟建一个更大的圆锥形仓库,以存放更多粮食.现有两种方案:一是新建的仓库的底面半径比原来大 (高不变);二是高度增加(底面直径不变).
(1) 分别计算按这两种方案所建的仓库的体积;
(2) 分别计算按这两种方案所建的仓库的表面积;
(3) 哪个方案更经济些?
数学试题
满分:150分 考试时间: 120分钟
注意事项:
1、答第I卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上;
2、每题选出答案后,用2B铅笔把答题卡对应题目的答案涂黑。如需改动,用橡皮擦干净后,再改涂在其它答案标号上;
3、填空题答案写在答题纸规定的题号处;
4、解答题应写出文字说明、推理或演算过程;每题务必在答题纸题号所指示的答题区域作答。
本试卷分第I卷(选择题)和第II卷(非选择题)两部分
第I卷(选择题 共60分)
一、选择题:(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求)
1.如下图所示,观察四个几何体,其中判断正确的是 【 】
A.①是棱台 B.②是圆台 C.③是棱锥 D.④不是棱柱
2、经过平面外三点,作与平面平行的平面,则这样的平面可以作 【 】
A. 0个 B. 1个 C. 0个或1个 D. 0个,1个或2个
3、下列命题正确的个数是 【 】
①棱柱的侧面为平行四边形;②正三棱锥也称正四面体;
③以直角三角形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆锥;
④圆台的任意两条母线的延长线(反向延长线)必交于一点。
A. 0个 B. 1个 C. 2个 D. 3个
4、已知函数 的反函数为,则 【 】
A. B.
C. D.
正方体的体积是64,则其表面积是 【 】
A.64 B.16 C.96 D.无法确定
将无盖正方体纸盒展开如右图,直线AB、CD在
原正方体中的位置关系是 【 】
A.平行 B.相交且垂直 C.异面直线 D.相交成
7、若轴截面为正方形的圆柱的侧面积是,
那么圆柱的体积为 【 】
A. B. C. D.
8、已知平面、和直线、,下列结论正确的是 【 】
A.若,则 B.若,则
C.若,且,则 D.若,且,则.
9、某几何体的正视图和侧视图均如左下图所示,则该几何体的俯视图不可能是 【 】
10、如右上图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为 【 】
A .,1 B.,1 C., D.,
11.若定义函数满足,(为常数),则称为等差函数,下列为等差函数的是 【 】
A. B. C. D.
12 .已知矩形将沿矩形的对角线折起,在翻折过程中【 】
A. 存在某个位置,使直线与直线垂直
B. 存在某个位置,使直线与直线垂直
C. 存在某个位置,使直线与直线垂直
D. 三对直线“与”,“与”,“与”始终都不垂直
第Ⅱ卷 (非选择题 共90分)
填空题:(本大题共4小题,每小题5分,满分20分)
13、已知函数,,则实数= .
14、将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的侧面积为 .
15、已知水平放置的△ABC按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么原△ABC的面积是 .
一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为3,则这个球的体积为 .
三、解答题:(本大题共6小题,共70分.解答应写出文字说明、推理过程或演算过程.)
17.(本小题满分10分)
如右图,在直三棱柱中,是上的一点,,且. 求证:平面。
(本小题满分12分)
如下图,在四棱锥中,底面是矩形.已知.
证明:平面平面.
19. (本小题满分12分)
已知函数;
(1)求函数的定义域;(2)判断函数的奇偶性,并说明理由。
20.(本小题满分12分)
如右图:为☉○的直径,☉○所在平面为水平放置,
平面,为☉○上异于的一点,
,点为的中点。
(1)求证:;
(2) 求三棱锥的表面积。
21.(本小题满分12分)
如图4:已知正四棱柱中,底面边长,侧棱的长为4,过点作的垂线交侧棱于点,交于点.
(1)求异面直线与夹角的正切值;
(2)求证:平面;
22.(本小题满分12分)
经开区建造圆锥形仓库用于贮藏粮食,已建的仓库的底面直径为,高为。随着经开区农业经济的发展,粮食产量增大,经开区现拟建一个更大的圆锥形仓库,以存放更多粮食.现有两种方案:一是新建的仓库的底面半径比原来大 (高不变);二是高度增加(底面直径不变).
(1) 分别计算按这两种方案所建的仓库的体积;
(2) 分别计算按这两种方案所建的仓库的表面积;
(3) 哪个方案更经济些?
同课章节目录
