沪科版九年级下第26章概率初步单元评估检测试卷(有答案)
文档属性
| 名称 | 沪科版九年级下第26章概率初步单元评估检测试卷(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 109.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-02 00:00:00 | ||
图片预览




文档简介
沪科版九年级数学下册 第26章 概率初步 单元评估检测试卷
一、单选题(共10题;共30分)
1.“a是实数,|a|≥0”这一事件是(???)
A.?必然事件?????????????????????????/B.?不确定事件?????????????????????????/C.?不可能事件?????????????????????????/D.?随机事件
2.在某次国际乒乓球单打比赛中,甲、乙两名中国选手进入最后决赛,那么下列事件为必然事件的是(???)
A.?冠军属于中国选手??????/B.?冠军属于外国选手??????/C.?冠军属于中国选手甲??????/D.?冠军属于中国选手乙
3.“买一张福利彩票,开奖后会中奖 ”这一事件是(????? )
A.?不可能事件??????????????????????????/B.?必然事件??????????????????????????/C.?随机事件??????????????????????????/D.?确定事件
4.在一个不透明的笔袋中装有两支黑色笔和一支红色笔,除颜色不同外其他都相同, 随机从其中摸出一支黑色笔的概率是
A.?
1
2
???????????????????????????????????????????/B.?
1
3
???????????????????????????????????????????/C.?
2
3
???????????????????????????????????????????/D.?1
5.一个不透明的布袋中装着只有颜色不同的红、黄两种小球,其中红色小球有8个,为估计袋中黄色小球的数目,每次将袋中小球搅匀后摸出一个小球记下颜色,然后放回袋中,再次搅匀……多次试验发现摸到红球的频率是
1
6
,则估计黄色小球的数目是(????)
A.?2个?????????????????????????????????????B.?20个?????????????????????????????????????C.?40个?????????????????????????????????????D.?48个
6.现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是(?? )
A.?
1
3
?????????????????????????????????????????/B.?
1
6
?????????????????????????????????????????/C.?
1
9
?????????????????????????????????????????/D.?
1
12
7.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的概率为
1
2
,那么口袋中球的总数为(???)
A.?12个??????????????????????????????????????/B.?9个??????????????????????????????????????/C.?6个??????????????????????????????????????/D.?3个
8.下列成语或词语所反映的事件中,可能性大小最小的是(?? )
A.?瓮中捉鳖???????????????????????????/B.?守株待兔???????????????????????????/C.?旭日东升???????????????????????????/D.?夕阳西下
9.学校新开设了航模、彩绘、泥塑三个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率是(? ?)
A.?
2
3
??????????????????????????????????????????/B.?
1
2
??????????????????????????????????????????/C.?
1
3
??????????????????????????????????????????/D.?
1
4
10.某班共有41名同学,其中有2名同学习惯用左手写字,其余同学都习惯用右手写字,老师随机请1名同学解答问题,习惯用左手写字的同学被选中的概率是(???)
A.?0?????????????????????????????????????????/B.?
1
41
?????????????????????????????????????????/C.?
2
41
?????????????????????????????????????????/D.?1
二、填空题(共10题;共30分)
11.在一个不透明的盒子中装有n个规格相同的乒乓球,其中有2个黄色球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到黄色球的频率稳定于0.2,那么可以推算出n大约是________.
12.一只口袋中放着8只红球和16只黑球,这两种球除颜色以外没有任何其他区别.从口袋中随机取出一个球,取出这个球是红球的概率为________.
13.一只不透明的袋子中装有红球和白球共30个,这些球除了颜色外都相同,校课外学习小组做摸球实验,将球搅匀后任意摸出一个球,记下颜色后放回,搅匀,通过多次重复试验,算得摸到红球的频率是0.2,则袋中有________个红球.
14.在一个不透明的盒子中装有12个白球,若干个黄球,它们除了颜色不同外,其余均相同.若从中随机摸出一个白球的概率是
1
3
,则黄球的个数是________.
15.从1,2,3,…9共9个数字中任取一个数字,取出数字为奇数的概率是________?.
16.某校准备组织师生观看北京奥运会球类比赛,在不同时间段里有3场比赛,其中2场是乒乓球赛,1场是羽毛球赛,从中任意选看2场,则选看的2场恰好都是乒乓球比赛的概率是________?.
17.如图,是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影,转动指针,指针落在有阴影的区域内的概率为a;如果投掷一枚硬币,正面向上的概率为b,则a________b(填“>”“<”或“=”) /
18.小强与小红两人下军棋,小强获胜的概率为46%,小红获胜的概率是30%,那么两人下一盘棋小红不输的概率是________.
19.某产品出现次品的概率为0.05,任意抽取这种产品600件,那么大约有________件是次品.
20.如图是一个转盘,转一次指针指向灰色部分的概率是________? /
三、解答题(共10题;共60分)
21.一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球除了颜色以外没有任何区别.若小王取出的第一个球是白色,将它放在桌上,闭上眼睛从袋中余下的球中再任意取出一个球,取出红球的概率是多少?
22.一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位上的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数.试问:按这种方法能组成哪些两位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
23.将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌上. (1)随机抽取一张,求抽到奇数的概率; (2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?用树状图(或列表法)表示所有可能出现的结果.这个两位数恰好是4的倍数的概率是多少?
24.某公司在羊年春节晚会上举行一个游戏,规则如下:有4张背面相同的卡片,正面分别是喜羊羊、美羊羊、慢羊羊、懒羊羊的头像,分别对应1000元、600元、400元、200元的奖金,现将4张纸牌洗匀后背面朝上摆放到桌上,让员工抽取,每人有两次抽奖机会,两次抽取的奖金之和作为公司发的年终奖金.现有两种抽取的方案:①小芳抽取方案是:直接从四张牌中抽取两张.②小明抽取的方案是:先从四张牌中抽取一张后放回去,再从四张中再抽取一张.你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金不少于1000元的概率大?请用树形图或列表法进行分析说明.
25.甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是________.
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
26.研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n
100
200
300
500
800
1000
摸到有记号球的次数m
25
44
57
105
160
199
摸到有记号球的频率[MISSING IMAGE: , ]
0.25
0.22
0.19
0.21
0.20
0.20
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
27.小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选. (1)用树状图或列表法求出小明先挑选的概率; (2)你认为这个游戏公平吗?请说明理由.
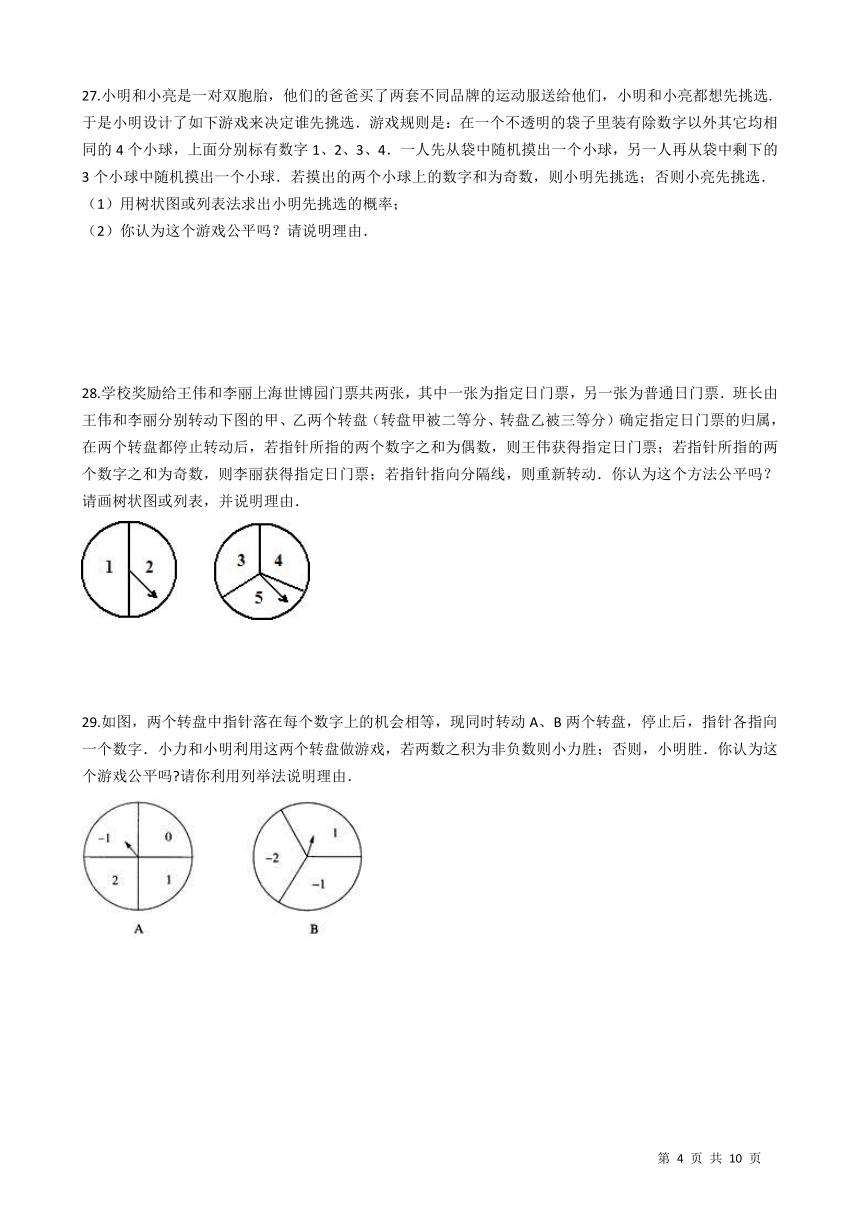
28.学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票.班长由王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动.你认为这个方法公平吗?请画树状图或列表,并说明理由. /
29.如图,两个转盘中指针落在每个数字上的机会相等,现同时转动A、B两个转盘,停止后,指针各指向一个数字.小力和小明利用这两个转盘做游戏,若两数之积为非负数则小力胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由. /
30.王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
2
5
6
4
10
3
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率; (2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由; (3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
答案解析部分
一、单选题
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】C
二、填空题
11.【答案】10
12.【答案】
1
3
13.【答案】6
14.【答案】24
15.【答案】/
16.【答案】
1
3
17.【答案】=
18.【答案】54%
19.【答案】30
20.【答案】
1
3
三、解答题
21.【答案】由于白球的数目减少了1个,故总数减小为19,所以取出红球的概率增加了,变为 /.
22.【答案】解:根据题意列表如下: / 十位上则十位上的数字和个位上的数字之和为9的两位数有45和54,所以其概率为:2÷9=
2
9
.
23.【答案】解:(1)P(抽到奇数)=
2
3
; (2)/ 能组成的两位数是12,13,21,23,31,32. ∴P(恰好是4的倍数)=
2
6
=
1
3
.
24.【答案】解:小芳抽取方案 画树状图为: / 共有12种等可能的结果数,其中抽取到的奖金不少于1000元的概率=
4
12
=
1
3
; 小明抽取的方案: / 共有16种等可能的结果数,其中抽取到的奖金不少于1000元的概率=
6
16
=
3
8
因为
1
3
<
3
8
, 所以小明抽到的奖金不少于1000元的概率大.
25.【答案】(1)
1
2
(2)解:将甲、乙两校报名的教师分别记为甲1、甲2、乙1、乙2(注:1表示男教师,2表示女教师),树状图如图所示:/ 所以P(两名教师来自同一所学校)=
4
12
=
1
3
?.
26.【答案】解:(1)根据105÷500=0.21,160÷800=0.2,199÷1000≈0.2,
故摸到有记号球的概率是:0.2;
(2)根据图表可以得出摸到有记号球的概率是0.2,
故盒中共有球:
8
??
=0.2,
解得:x=40,
故没有记号球有40﹣8=32个.
27.【答案】解:(1)根据题意可列表如下:
第一次 第二次
1
2
3
4
1
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,4)
4
(4,1)
(4,2)
(4,3)
从表可以看出所有可能结果共有12种,且每种结果发生的可能性相同,符合条件的结果有8种, ∴P(和为奇数)=
8
12
=
2
3
; (2)不公平. ∵小明先挑选的概率是P(和为奇数)=
2
3
,小亮先挑选的概率是P(和为偶数)=
1
3
, ∵
2
3
≠
1
3
, ∴不公平.
28.【答案】解: / 共有6种情况,指针所指的两个数字之和为偶数的情况有3种, 因此王伟获胜的概率为
3
6
=
1
2
,李丽获胜的概率是
1
2
,所以这个方法公平.
29.【答案】解:根据题意列树状图如下: / 由树状图可知,游戏结果有12中情况,其中两数之积为非负有7种,则两数之积为非负的概率为
7
12
,两数之积为负的情况有5种,则两数之积为为负的概率为
5
12
.
5
12
≠
7
12
,因此该游戏不公平。
30.【答案】解:(1)“3点朝上”的频率为:
6
30
=
1
5
, “5点朝上”的频率为:
10
30
=
1
3
; (2)王勇的说法是错误的 因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大, 只有当实验次数足够大时,该事件发生的频率才能稳定在事件发生的概率附近,也才能用该事件发生的频率区估计其概率. 李明的说法也是错误的,因为事件的发生具有随机性,所以投掷300次,出现“6点朝上”的次数不一定是30次. (3)列表:
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
∵朝上的点数之和为3的倍数共有12个, ∴P(点数之和为3的倍数)=
12
36
=
1
3
?.
一、单选题(共10题;共30分)
1.“a是实数,|a|≥0”这一事件是(???)
A.?必然事件?????????????????????????/B.?不确定事件?????????????????????????/C.?不可能事件?????????????????????????/D.?随机事件
2.在某次国际乒乓球单打比赛中,甲、乙两名中国选手进入最后决赛,那么下列事件为必然事件的是(???)
A.?冠军属于中国选手??????/B.?冠军属于外国选手??????/C.?冠军属于中国选手甲??????/D.?冠军属于中国选手乙
3.“买一张福利彩票,开奖后会中奖 ”这一事件是(????? )
A.?不可能事件??????????????????????????/B.?必然事件??????????????????????????/C.?随机事件??????????????????????????/D.?确定事件
4.在一个不透明的笔袋中装有两支黑色笔和一支红色笔,除颜色不同外其他都相同, 随机从其中摸出一支黑色笔的概率是
A.?
1
2
???????????????????????????????????????????/B.?
1
3
???????????????????????????????????????????/C.?
2
3
???????????????????????????????????????????/D.?1
5.一个不透明的布袋中装着只有颜色不同的红、黄两种小球,其中红色小球有8个,为估计袋中黄色小球的数目,每次将袋中小球搅匀后摸出一个小球记下颜色,然后放回袋中,再次搅匀……多次试验发现摸到红球的频率是
1
6
,则估计黄色小球的数目是(????)
A.?2个?????????????????????????????????????B.?20个?????????????????????????????????????C.?40个?????????????????????????????????????D.?48个
6.现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是(?? )
A.?
1
3
?????????????????????????????????????????/B.?
1
6
?????????????????????????????????????????/C.?
1
9
?????????????????????????????????????????/D.?
1
12
7.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有3个红球且摸到红球的概率为
1
2
,那么口袋中球的总数为(???)
A.?12个??????????????????????????????????????/B.?9个??????????????????????????????????????/C.?6个??????????????????????????????????????/D.?3个
8.下列成语或词语所反映的事件中,可能性大小最小的是(?? )
A.?瓮中捉鳖???????????????????????????/B.?守株待兔???????????????????????????/C.?旭日东升???????????????????????????/D.?夕阳西下
9.学校新开设了航模、彩绘、泥塑三个社团,如果征征、舟舟两名同学每人随机选择参加其中一个社团,那么征征和舟舟选到同一社团的概率是(? ?)
A.?
2
3
??????????????????????????????????????????/B.?
1
2
??????????????????????????????????????????/C.?
1
3
??????????????????????????????????????????/D.?
1
4
10.某班共有41名同学,其中有2名同学习惯用左手写字,其余同学都习惯用右手写字,老师随机请1名同学解答问题,习惯用左手写字的同学被选中的概率是(???)
A.?0?????????????????????????????????????????/B.?
1
41
?????????????????????????????????????????/C.?
2
41
?????????????????????????????????????????/D.?1
二、填空题(共10题;共30分)
11.在一个不透明的盒子中装有n个规格相同的乒乓球,其中有2个黄色球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到黄色球的频率稳定于0.2,那么可以推算出n大约是________.
12.一只口袋中放着8只红球和16只黑球,这两种球除颜色以外没有任何其他区别.从口袋中随机取出一个球,取出这个球是红球的概率为________.
13.一只不透明的袋子中装有红球和白球共30个,这些球除了颜色外都相同,校课外学习小组做摸球实验,将球搅匀后任意摸出一个球,记下颜色后放回,搅匀,通过多次重复试验,算得摸到红球的频率是0.2,则袋中有________个红球.
14.在一个不透明的盒子中装有12个白球,若干个黄球,它们除了颜色不同外,其余均相同.若从中随机摸出一个白球的概率是
1
3
,则黄球的个数是________.
15.从1,2,3,…9共9个数字中任取一个数字,取出数字为奇数的概率是________?.
16.某校准备组织师生观看北京奥运会球类比赛,在不同时间段里有3场比赛,其中2场是乒乓球赛,1场是羽毛球赛,从中任意选看2场,则选看的2场恰好都是乒乓球比赛的概率是________?.
17.如图,是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影,转动指针,指针落在有阴影的区域内的概率为a;如果投掷一枚硬币,正面向上的概率为b,则a________b(填“>”“<”或“=”) /
18.小强与小红两人下军棋,小强获胜的概率为46%,小红获胜的概率是30%,那么两人下一盘棋小红不输的概率是________.
19.某产品出现次品的概率为0.05,任意抽取这种产品600件,那么大约有________件是次品.
20.如图是一个转盘,转一次指针指向灰色部分的概率是________? /
三、解答题(共10题;共60分)
21.一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球除了颜色以外没有任何区别.若小王取出的第一个球是白色,将它放在桌上,闭上眼睛从袋中余下的球中再任意取出一个球,取出红球的概率是多少?
22.一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位上的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数.试问:按这种方法能组成哪些两位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
23.将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌上. (1)随机抽取一张,求抽到奇数的概率; (2)随机抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?用树状图(或列表法)表示所有可能出现的结果.这个两位数恰好是4的倍数的概率是多少?
24.某公司在羊年春节晚会上举行一个游戏,规则如下:有4张背面相同的卡片,正面分别是喜羊羊、美羊羊、慢羊羊、懒羊羊的头像,分别对应1000元、600元、400元、200元的奖金,现将4张纸牌洗匀后背面朝上摆放到桌上,让员工抽取,每人有两次抽奖机会,两次抽取的奖金之和作为公司发的年终奖金.现有两种抽取的方案:①小芳抽取方案是:直接从四张牌中抽取两张.②小明抽取的方案是:先从四张牌中抽取一张后放回去,再从四张中再抽取一张.你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金不少于1000元的概率大?请用树形图或列表法进行分析说明.
25.甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是________.
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
26.研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n
100
200
300
500
800
1000
摸到有记号球的次数m
25
44
57
105
160
199
摸到有记号球的频率[MISSING IMAGE: , ]
0.25
0.22
0.19
0.21
0.20
0.20
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
27.小明和小亮是一对双胞胎,他们的爸爸买了两套不同品牌的运动服送给他们,小明和小亮都想先挑选.于是小明设计了如下游戏来决定谁先挑选.游戏规则是:在一个不透明的袋子里装有除数字以外其它均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为奇数,则小明先挑选;否则小亮先挑选. (1)用树状图或列表法求出小明先挑选的概率; (2)你认为这个游戏公平吗?请说明理由.
28.学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票.班长由王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动.你认为这个方法公平吗?请画树状图或列表,并说明理由. /
29.如图,两个转盘中指针落在每个数字上的机会相等,现同时转动A、B两个转盘,停止后,指针各指向一个数字.小力和小明利用这两个转盘做游戏,若两数之积为非负数则小力胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由. /
30.王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
2
5
6
4
10
3
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率; (2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由; (3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
答案解析部分
一、单选题
1.【答案】A
2.【答案】A
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】C
10.【答案】C
二、填空题
11.【答案】10
12.【答案】
1
3
13.【答案】6
14.【答案】24
15.【答案】/
16.【答案】
1
3
17.【答案】=
18.【答案】54%
19.【答案】30
20.【答案】
1
3
三、解答题
21.【答案】由于白球的数目减少了1个,故总数减小为19,所以取出红球的概率增加了,变为 /.
22.【答案】解:根据题意列表如下: / 十位上则十位上的数字和个位上的数字之和为9的两位数有45和54,所以其概率为:2÷9=
2
9
.
23.【答案】解:(1)P(抽到奇数)=
2
3
; (2)/ 能组成的两位数是12,13,21,23,31,32. ∴P(恰好是4的倍数)=
2
6
=
1
3
.
24.【答案】解:小芳抽取方案 画树状图为: / 共有12种等可能的结果数,其中抽取到的奖金不少于1000元的概率=
4
12
=
1
3
; 小明抽取的方案: / 共有16种等可能的结果数,其中抽取到的奖金不少于1000元的概率=
6
16
=
3
8
因为
1
3
<
3
8
, 所以小明抽到的奖金不少于1000元的概率大.
25.【答案】(1)
1
2
(2)解:将甲、乙两校报名的教师分别记为甲1、甲2、乙1、乙2(注:1表示男教师,2表示女教师),树状图如图所示:/ 所以P(两名教师来自同一所学校)=
4
12
=
1
3
?.
26.【答案】解:(1)根据105÷500=0.21,160÷800=0.2,199÷1000≈0.2,
故摸到有记号球的概率是:0.2;
(2)根据图表可以得出摸到有记号球的概率是0.2,
故盒中共有球:
8
??
=0.2,
解得:x=40,
故没有记号球有40﹣8=32个.
27.【答案】解:(1)根据题意可列表如下:
第一次 第二次
1
2
3
4
1
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,4)
4
(4,1)
(4,2)
(4,3)
从表可以看出所有可能结果共有12种,且每种结果发生的可能性相同,符合条件的结果有8种, ∴P(和为奇数)=
8
12
=
2
3
; (2)不公平. ∵小明先挑选的概率是P(和为奇数)=
2
3
,小亮先挑选的概率是P(和为偶数)=
1
3
, ∵
2
3
≠
1
3
, ∴不公平.
28.【答案】解: / 共有6种情况,指针所指的两个数字之和为偶数的情况有3种, 因此王伟获胜的概率为
3
6
=
1
2
,李丽获胜的概率是
1
2
,所以这个方法公平.
29.【答案】解:根据题意列树状图如下: / 由树状图可知,游戏结果有12中情况,其中两数之积为非负有7种,则两数之积为非负的概率为
7
12
,两数之积为负的情况有5种,则两数之积为为负的概率为
5
12
.
5
12
≠
7
12
,因此该游戏不公平。
30.【答案】解:(1)“3点朝上”的频率为:
6
30
=
1
5
, “5点朝上”的频率为:
10
30
=
1
3
; (2)王勇的说法是错误的 因为“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的概率最大, 只有当实验次数足够大时,该事件发生的频率才能稳定在事件发生的概率附近,也才能用该事件发生的频率区估计其概率. 李明的说法也是错误的,因为事件的发生具有随机性,所以投掷300次,出现“6点朝上”的次数不一定是30次. (3)列表:
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
∵朝上的点数之和为3的倍数共有12个, ∴P(点数之和为3的倍数)=
12
36
=
1
3
?.
