九年级上第23章解直角三角形期末专题复习试卷(含答案)
文档属性
| 名称 | 九年级上第23章解直角三角形期末专题复习试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-02 00:00:00 | ||
图片预览




文档简介
期末专题复习:沪科版九年级数学上册 第23章 解直角三角形 单元评估检测试卷
一、单选题(共10题;共30分)
1.sin30°的值等于(?????)
A.?
1
2
????????????????????????????????????????/B.?
2
2
????????????????????????????????????????/C.?
3
2
????????????????????????????????????????/D.?1
2.如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为(? ? ? ) A.?1.8tan80°m?????????/B.?1.8cos80°m??????????????????????/C.?1.8sin 80°m??????????????????????/D.?
1.8
tan
80
°
m
3.如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠A的值为( ??)
/
A.?
6
5
??????????????????????????????????????/B.?
5
6
??????????????????????????????????????/C.?
34
3
??????????????????????????????????????/D.?
5
61
61
4.如图,在菱形ABCD中,∠ADC=120°,则BD:AC等于( ) /
A.?
3
:2?????????????????????????????????/B.?3:3?????????????????????????????????/C.?1:2?????????????????????????????????/D.?3:1
5.在Rt△ABC中,∠C=90°,sinA=
4
5
,则cosB的值等于( )
A.?
3
5
?????????????????????????????????????????/B.?
4
5
?????????????????????????????????????????/C.?
3
4
?????????????????????????????????????????/D.?
5
5
6.已知:Rt△ABC中,∠C=90°,cosA=
3
5
,AB=15,则AC的长是(?? )
A.?3??????????????????????????????????????????/B.?6??????????????????????????????????????????/C.?9??????????????????????????????????????????/D.?12
7.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,下列结论正确的是(??) /
A.?sinA=
3
2
??????????????????????????B.?tanA=
1
2
??????????????????????????C.?cosB=
3
2
??????????????????????????D.?tanB=
3
8.这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5
5
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)(?? ) /
A.?7米???????????????????????????????????/B.?7.2米???????????????????????????????????/C.?9.7米???????????????????????????????????/D.?15.5米
9.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( ) /
A.?(6+
3
)米???????????????????????????/B.?12米???????????????????????????/C.?(4+2
3
)米???????????????????????????/D.?10米
10.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
5
cm,且tan∠EFC=
3
4
,那么该矩形的周长为() /
A.?72cm??????????????????????????????????B.?36cm??????????????????????????????????C.?20cm??????????????????????????????????D.?16cm
二、填空题(共10题;共30分)
11.计算: 2
sin
2
45
o
?tan
45
o
= ________.
12.如图,在平行四边形ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8, sin??=
4
5
,那么EC=________.? /
13.如图,某汽车从A处出发准备开往正北方向M处,但是由于AM之间道路正在整修,所以需先到B处,再到M处,若B在A的北偏东25°,汽车到B处发现,此时正好BM=BA,则汽车要想到达M处,此时应沿北偏西________的方向行驶.
/
14.小明沿着坡度为1:
3
的坡面向下走了20米的路,那么他竖直方向下降的高度为________.
15.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=10
2
米,背水坡CD的坡度i=1:
3
,则背水坡的坡长CD为________米.
/
16.(2011?义乌市)如图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是 5
2
m,则乘电梯从点B到点C上升的高度h是________?m. /
17.在△ABC中,若|cosA-
3
2
|+(1-tanB)2=0,则∠C的度数是________.
18.(2016?新疆)如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为________m(结果保留根号).
/
19.如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为________. /
20.如图,已知等边三角形OAB与反比例函数y=
??
??
(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则
????
????
的值为________.(已知sin15°=
6
?
2
4
) /
三、解答题(共10题;共60分)
21.计算 |
2
?2|?2cos
45
°
+
(?1)
?2
+
8
.
22.甲、乙两船同时从港口A出发,甲船以12海里/时的速度向 北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距30海里,问乙船的速度是每小时多少海里? /
23.如图,某游客在山脚下乘览车上山.导游告知,索道与水平线成角∠BAC为40°,览车速度为60米/分,11分钟到达山顶,请根据以上信息计算山的高度BC. (精确到1米)(参考数据:sin40°=0.64,cos40°=0.77,tan40°=0.84) /
24.如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离. /
25.在一次暑假旅游中,小亮在仙岛湖的游船上(A处),测得湖西岸的山峰太婆尖(C处)和湖东岸的山峰老君岭(D处)的仰角都是45°.游船向东航行100米后(B处),测得太婆尖,老君岭的仰角分别为30°,60°.试问太婆尖、老君岭的高度为多少米? /
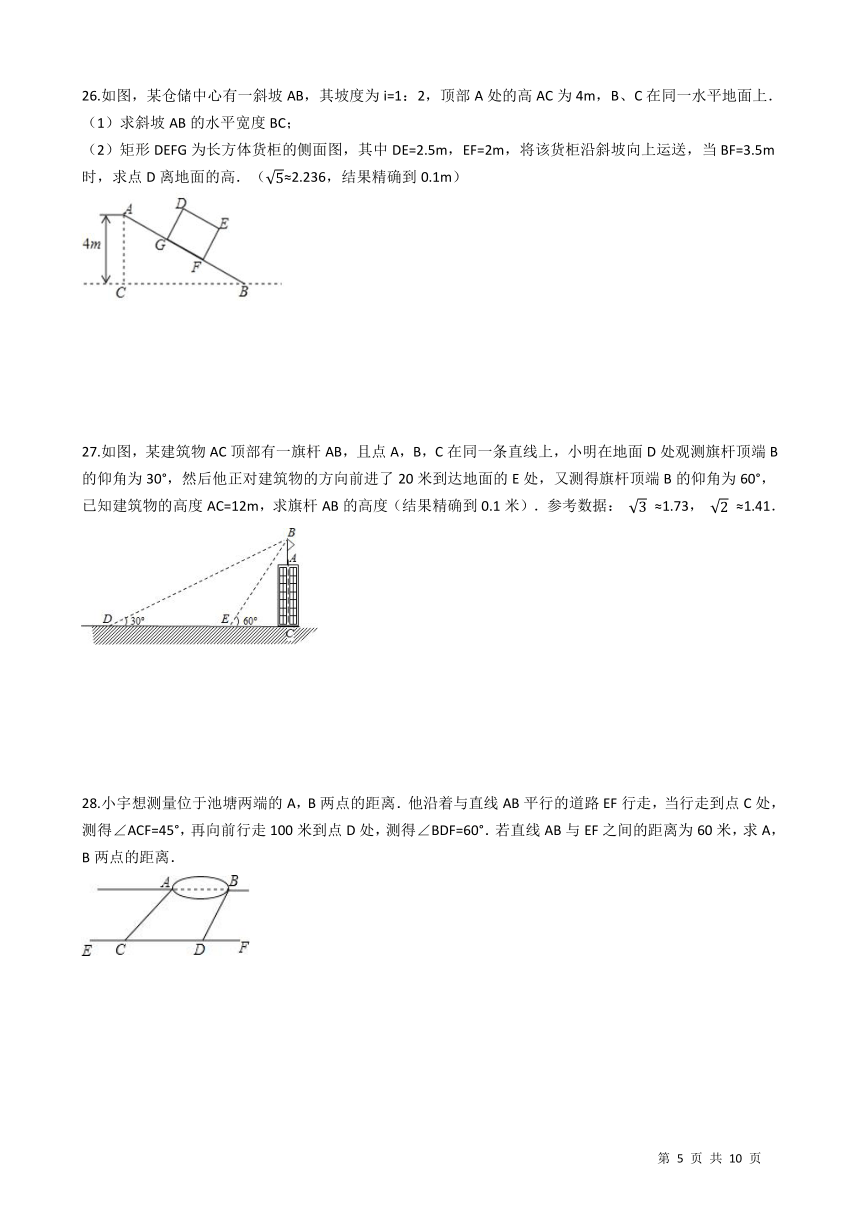
26.如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上. (1)求斜坡AB的水平宽度BC; (2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(
5
≈2.236,结果精确到0.1m) /
27.如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:
3
≈1.73,
2
≈1.41. /
28.小宇想测量位于池塘两端的A,B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A,B两点的距离. /
29.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值) . /?
30.如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东
30
°
方向以每小时15海里的速度航行,甲沿南偏西
75
°
方向以每小时 15
2
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东
60
°
方向追赶乙船,正好在B处追上 . 甲船追赶乙船的速度为多少海里 / 小时?
/
答案解析部分
一、单选题
1.【答案】A
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】A
10.【答案】A
二、填空题
11.【答案】0
12.【答案】5
13.【答案】25°
14.【答案】10米
15.【答案】20
16.【答案】5
17.【答案】105°
18.【答案】30
3
19.【答案】
5
?1
2
20.【答案】
3
?1
2
三、解答题
21.【答案】解:原式=2-
2
-2×
2
2
+1+2
2
. ?????????? ?? =3.
22.【答案】解:根据题意得:AC=12×2=24,BC=30,∠BAC=90°. ∴AC2+AB2=BC2 . ∴AB2=BC2-AC2=302-242=324 ∴AB=18. ∴乙船的航速是:18÷2=9海里/时.
23.【答案】解:由题意可得:∠BAC=40°,AB=66米. ∵sin40°=
????
????
,∴BC≈0.64×660=422.4米≈422米. 答:山的高度BC约为422米.
24.【答案】由题意可知:∠CDA=90°; 在Rt△CAD中,∠CDA=90°,∠CAD=45°,CD=15, ∴/. 在Rt△CDN中,∠CDN=90°,∠CND=30°, ∴/. ∴/(米). 故A、N之间的距离为(/)米.
25.【答案】解:过点C作CE⊥AB于E和过点D作DF⊥AB于F, 设太婆尖高h1米,老君岭高h2米, 则根据BE﹣AE=AB和AF﹣BF=AB得: {
?
1
tan
30
0
?
?
1
tan
45
0
=100
?
2
tan
45
0
?
?
2
tan
60
0
=100
? ∴h1=
100
tan
60
0
?tan
45
0
=50(
3
+1)=50(1.732+1)=136.6≈137(米) h2=
100
tan
45
0
?tan
30
0
=
100
1?
3
3
=
100(1+
3
3
)
(1?
3
3
)(1+
3
3
)
=50
3
(
3
+1)=50(3+1.732)=236.6≈237(米) 答:太婆尖高度为137米,老君岭高度为237米. /
26.【答案】【解答】解:(1)∵坡度为i=1:2,AC=4m, ∴BC=4×2=8m. (2)作DS⊥BC,垂足为S,且与AB相交于H. ∵∠DGH=∠BSH,∠DHG=∠BHS, ∴∠GDH=∠SBH, ∴
????
????
=
1
2
, ∵DG=EF=2m, ∴GH=1m, ∴DH=
1
2
+
2
2
=
5
m,BH=BF+FH=3.5+(2.5﹣1)=5m, 设HS=xm,则BS=2xm, ∴x2+(2x)2=52 , ∴x=
5
m, ∴DS=
5
+
5
=2
5
m≈4.5m. /
27.【答案】解:∵∠BEC=60°,∠BDE=30°, ∴∠DBE=60°﹣30°=30°, ∴BE=DE=20, 在Rt△BEC中, BC=BE?sin60°=20×
3
2
=10
3
≈17.3(米), ∴AB=BC﹣AC=17.3﹣12=5.3(米), 答:旗杆AB的高度为5.3米.
28.【答案】解:作AM⊥EF于点M,作BN⊥EF于点N,如右图所示, / 由题意可得,AM=BN=60米,CD=100米,∠ACF=45°,∠BDF=60°, ∴CM=
????
??????45°
=
60
1
=60 米, DN=
????
??????60°
=
60
3
=20
3
米, ∴AB=CD+DN﹣CM=100+20
3
﹣60=(40+20
3
)米, 即A、B两点的距离是(40+20
3
)米.
29.【答案】解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F , / 则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF . 在Rt△BCE中,∵∠E=90°,∠CBE=60°, ∴∠BCE=30°, ∴BE= /BC= /×1000=500米; 在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=AB=1000米, ∴CF= /CD=500 /米, ∴DA=BE+CF=(500+500 /)米, 故拦截点D处到公路的距离是(500+500 /)米 . ?
30.【答案】解:过O作 ????⊥???? 于C.
/
由题意可得: ∠??????=
180
°
?
60
°
?
75
°
=
45
°
, ????=15
2
( 海里 ) ,
∴ ????=????=15
2
×
2
2
=15( 海里 ) ,
∵ ∠??=
90
°
?
30
°
?
30
°
=
30
°
,
∴
????
????
=tan
30
°
,
∴
15
????
=
3
3
,
∴ ????=15
3
( 海里 ) ,
????=15×2=30( 海里 ) ,
乙船从O点到B点所需时间为2小时,
∴甲船追赶乙船速度为 (15+15
3
) 海里 / 小时.
一、单选题(共10题;共30分)
1.sin30°的值等于(?????)
A.?
1
2
????????????????????????????????????????/B.?
2
2
????????????????????????????????????????/C.?
3
2
????????????????????????????????????????/D.?1
2.如图,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为(? ? ? ) A.?1.8tan80°m?????????/B.?1.8cos80°m??????????????????????/C.?1.8sin 80°m??????????????????????/D.?
1.8
tan
80
°
m
3.如图,△ABC的三个顶点都在正方形网格的格点上,则sin∠A的值为( ??)
/
A.?
6
5
??????????????????????????????????????/B.?
5
6
??????????????????????????????????????/C.?
34
3
??????????????????????????????????????/D.?
5
61
61
4.如图,在菱形ABCD中,∠ADC=120°,则BD:AC等于( ) /
A.?
3
:2?????????????????????????????????/B.?3:3?????????????????????????????????/C.?1:2?????????????????????????????????/D.?3:1
5.在Rt△ABC中,∠C=90°,sinA=
4
5
,则cosB的值等于( )
A.?
3
5
?????????????????????????????????????????/B.?
4
5
?????????????????????????????????????????/C.?
3
4
?????????????????????????????????????????/D.?
5
5
6.已知:Rt△ABC中,∠C=90°,cosA=
3
5
,AB=15,则AC的长是(?? )
A.?3??????????????????????????????????????????/B.?6??????????????????????????????????????????/C.?9??????????????????????????????????????????/D.?12
7.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,下列结论正确的是(??) /
A.?sinA=
3
2
??????????????????????????B.?tanA=
1
2
??????????????????????????C.?cosB=
3
2
??????????????????????????D.?tanB=
3
8.这次数学实践课上,同学进行大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为37°,然后沿在同一剖面的斜坡AB行走5
5
米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度i=1:2(通常把坡面的垂直高度h和水平宽度l的比叫做坡度,即tanα值(α为斜坡与水平面夹角),那么大树CD的高度约为(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)(?? ) /
A.?7米???????????????????????????????????/B.?7.2米???????????????????????????????????/C.?9.7米???????????????????????????????????/D.?15.5米
9.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( ) /
A.?(6+
3
)米???????????????????????????/B.?12米???????????????????????????/C.?(4+2
3
)米???????????????????????????/D.?10米
10.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10
5
cm,且tan∠EFC=
3
4
,那么该矩形的周长为() /
A.?72cm??????????????????????????????????B.?36cm??????????????????????????????????C.?20cm??????????????????????????????????D.?16cm
二、填空题(共10题;共30分)
11.计算: 2
sin
2
45
o
?tan
45
o
= ________.
12.如图,在平行四边形ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8, sin??=
4
5
,那么EC=________.? /
13.如图,某汽车从A处出发准备开往正北方向M处,但是由于AM之间道路正在整修,所以需先到B处,再到M处,若B在A的北偏东25°,汽车到B处发现,此时正好BM=BA,则汽车要想到达M处,此时应沿北偏西________的方向行驶.
/
14.小明沿着坡度为1:
3
的坡面向下走了20米的路,那么他竖直方向下降的高度为________.
15.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=10
2
米,背水坡CD的坡度i=1:
3
,则背水坡的坡长CD为________米.
/
16.(2011?义乌市)如图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是 5
2
m,则乘电梯从点B到点C上升的高度h是________?m. /
17.在△ABC中,若|cosA-
3
2
|+(1-tanB)2=0,则∠C的度数是________.
18.(2016?新疆)如图,测量河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为________m(结果保留根号).
/
19.如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为________. /
20.如图,已知等边三角形OAB与反比例函数y=
??
??
(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则
????
????
的值为________.(已知sin15°=
6
?
2
4
) /
三、解答题(共10题;共60分)
21.计算 |
2
?2|?2cos
45
°
+
(?1)
?2
+
8
.
22.甲、乙两船同时从港口A出发,甲船以12海里/时的速度向 北偏东35°航行,乙船向南偏东55°航行,2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距30海里,问乙船的速度是每小时多少海里? /
23.如图,某游客在山脚下乘览车上山.导游告知,索道与水平线成角∠BAC为40°,览车速度为60米/分,11分钟到达山顶,请根据以上信息计算山的高度BC. (精确到1米)(参考数据:sin40°=0.64,cos40°=0.77,tan40°=0.84) /
24.如图,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离. /
25.在一次暑假旅游中,小亮在仙岛湖的游船上(A处),测得湖西岸的山峰太婆尖(C处)和湖东岸的山峰老君岭(D处)的仰角都是45°.游船向东航行100米后(B处),测得太婆尖,老君岭的仰角分别为30°,60°.试问太婆尖、老君岭的高度为多少米? /
26.如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上. (1)求斜坡AB的水平宽度BC; (2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(
5
≈2.236,结果精确到0.1m) /
27.如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:
3
≈1.73,
2
≈1.41. /
28.小宇想测量位于池塘两端的A,B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A,B两点的距离. /
29.如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值) . /?
30.如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东
30
°
方向以每小时15海里的速度航行,甲沿南偏西
75
°
方向以每小时 15
2
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东
60
°
方向追赶乙船,正好在B处追上 . 甲船追赶乙船的速度为多少海里 / 小时?
/
答案解析部分
一、单选题
1.【答案】A
2.【答案】D
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】A
10.【答案】A
二、填空题
11.【答案】0
12.【答案】5
13.【答案】25°
14.【答案】10米
15.【答案】20
16.【答案】5
17.【答案】105°
18.【答案】30
3
19.【答案】
5
?1
2
20.【答案】
3
?1
2
三、解答题
21.【答案】解:原式=2-
2
-2×
2
2
+1+2
2
. ?????????? ?? =3.
22.【答案】解:根据题意得:AC=12×2=24,BC=30,∠BAC=90°. ∴AC2+AB2=BC2 . ∴AB2=BC2-AC2=302-242=324 ∴AB=18. ∴乙船的航速是:18÷2=9海里/时.
23.【答案】解:由题意可得:∠BAC=40°,AB=66米. ∵sin40°=
????
????
,∴BC≈0.64×660=422.4米≈422米. 答:山的高度BC约为422米.
24.【答案】由题意可知:∠CDA=90°; 在Rt△CAD中,∠CDA=90°,∠CAD=45°,CD=15, ∴/. 在Rt△CDN中,∠CDN=90°,∠CND=30°, ∴/. ∴/(米). 故A、N之间的距离为(/)米.
25.【答案】解:过点C作CE⊥AB于E和过点D作DF⊥AB于F, 设太婆尖高h1米,老君岭高h2米, 则根据BE﹣AE=AB和AF﹣BF=AB得: {
?
1
tan
30
0
?
?
1
tan
45
0
=100
?
2
tan
45
0
?
?
2
tan
60
0
=100
? ∴h1=
100
tan
60
0
?tan
45
0
=50(
3
+1)=50(1.732+1)=136.6≈137(米) h2=
100
tan
45
0
?tan
30
0
=
100
1?
3
3
=
100(1+
3
3
)
(1?
3
3
)(1+
3
3
)
=50
3
(
3
+1)=50(3+1.732)=236.6≈237(米) 答:太婆尖高度为137米,老君岭高度为237米. /
26.【答案】【解答】解:(1)∵坡度为i=1:2,AC=4m, ∴BC=4×2=8m. (2)作DS⊥BC,垂足为S,且与AB相交于H. ∵∠DGH=∠BSH,∠DHG=∠BHS, ∴∠GDH=∠SBH, ∴
????
????
=
1
2
, ∵DG=EF=2m, ∴GH=1m, ∴DH=
1
2
+
2
2
=
5
m,BH=BF+FH=3.5+(2.5﹣1)=5m, 设HS=xm,则BS=2xm, ∴x2+(2x)2=52 , ∴x=
5
m, ∴DS=
5
+
5
=2
5
m≈4.5m. /
27.【答案】解:∵∠BEC=60°,∠BDE=30°, ∴∠DBE=60°﹣30°=30°, ∴BE=DE=20, 在Rt△BEC中, BC=BE?sin60°=20×
3
2
=10
3
≈17.3(米), ∴AB=BC﹣AC=17.3﹣12=5.3(米), 答:旗杆AB的高度为5.3米.
28.【答案】解:作AM⊥EF于点M,作BN⊥EF于点N,如右图所示, / 由题意可得,AM=BN=60米,CD=100米,∠ACF=45°,∠BDF=60°, ∴CM=
????
??????45°
=
60
1
=60 米, DN=
????
??????60°
=
60
3
=20
3
米, ∴AB=CD+DN﹣CM=100+20
3
﹣60=(40+20
3
)米, 即A、B两点的距离是(40+20
3
)米.
29.【答案】解:如图,过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F , / 则∠E=∠F=90°,拦截点D处到公路的距离DA=BE+CF . 在Rt△BCE中,∵∠E=90°,∠CBE=60°, ∴∠BCE=30°, ∴BE= /BC= /×1000=500米; 在Rt△CDF中,∵∠F=90°,∠DCF=45°,CD=AB=1000米, ∴CF= /CD=500 /米, ∴DA=BE+CF=(500+500 /)米, 故拦截点D处到公路的距离是(500+500 /)米 . ?
30.【答案】解:过O作 ????⊥???? 于C.
/
由题意可得: ∠??????=
180
°
?
60
°
?
75
°
=
45
°
, ????=15
2
( 海里 ) ,
∴ ????=????=15
2
×
2
2
=15( 海里 ) ,
∵ ∠??=
90
°
?
30
°
?
30
°
=
30
°
,
∴
????
????
=tan
30
°
,
∴
15
????
=
3
3
,
∴ ????=15
3
( 海里 ) ,
????=15×2=30( 海里 ) ,
乙船从O点到B点所需时间为2小时,
∴甲船追赶乙船速度为 (15+15
3
) 海里 / 小时.
