九年级上册第21章二次函数与反比例函数期末专题复习试卷(有答案)
文档属性
| 名称 | 九年级上册第21章二次函数与反比例函数期末专题复习试卷(有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 104.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-02 08:48:08 | ||
图片预览




文档简介
期末专题复习:沪科版九年级数学上册 第21章 二次函数与反比例函数 单元评估检测试卷
一、单选题(共10题;共30分)
1.抛物线y=(x﹣2)2+3的对称轴是(?? )
A.?直线x=2??????????????????????????B.?直线x=3??????????????????????????C.?直线x=﹣2??????????????????????????D.?直线x=﹣3
2.已知反比例函数y=
6
??
,下列各点不在该函数图象上的是(?? )
A.?(2,3)??????????/B.?(﹣2,﹣3)??????????/C.?(-3,-2)? ??????????/D.?? (-1,6)
3.抛物线y=2(x﹣3)2+1的顶点坐标是(? )
A.?(3,1)??????????????????????/B.?(3,﹣1)??????????????????????/C.?(﹣3,1)??????????????????????/D.?(﹣3,﹣1)
4.反比例函数 ??=?
3
??
的图象上有
??
1
(
??
1
,?2),
??
2
(
??
2
,?3) ?两点,则
??
1
与
??
2
的大小关系是(?? )
A.?
??
1
>
??
2
????????????????????????????????/B.?
??
1
=
??
2
????????????????????????????????/C.?
??
1
<
??
2
????????????????????????????????/D.?不确定
5.若反比例函数y=
??
??
的图象位于第二、四象限,则k的取值可能是( )
A.?-1 ???/B.?2 ???/C.?3 ?/D.?4
6.关于函数y=(500﹣10x)(40+x),下列说法不正确的是( )
A.?y是x的二次函数??????????????/B.?二次项系数是﹣10?????????????/C.?一次项是100?????????????/D.?常数项是20000
7.已知正方形ABCD,设AB=x,则正方形的面积y与x之间的函数关系式为( )
A.?y=4x??????????????????????????????????/B.?y=x2??????????????????????????????????/C.?x=
??
4
??????????????????????????????????/D.???=
??
8.若二次函数y=x2-6x+c的图象过A(-1,y1)、B(2,y2)、C(3+
2
,y3)三点,则y1、y2、y3的大小关系正确的是( ??????)
A.?y1>y2>y3??????????????????????/B.?y1>y3>y2??????????????????????/C.?y2>y1>y3??????????????????????/D.?y3>y1>y2
9.(2016?湖北)一次函数y=ax+b和反比例函数y=
??
??
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) /
A.?/????????????/B.?/????????????/C.?/????????????/D.?/
10.(2017?滨州)在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=
1
??
相交于点A、B,且AC+BC=4,则△OAB的面积为(??? )
A.?2
3
+3或2
3
﹣3??????????????????/B.?
2
+1或
2
﹣1??????????????????/C.?2
3
﹣3??????????????????/D.?
2
﹣1
二、填空题(共10题;共30分)
11.二次函数y=x2﹣2x﹣5的最小值是________.
12.如果抛物线y=(a+1)x2﹣4有最高点,那么a的取值范围是________.
13.如图,直线y=
1
2
x与双曲线y=
??
??
在第一象限的交点为A(2,m),则k=________. /
14.经过A(4,0),B(﹣2,0),C(0,3)三点的抛物线解析式是________.
15.二次函数 ??=
??
2
?6??+?? 的图象的顶点与原点的距离为5,则c=________。
16.试写出一个二次函数关系式,使它对应的一元二次方程的一个根为0,另一个根在1到2之间:________.
17.如图所示的二次函数 ??=??
??
2
+????+??(??≠0) 的图象中,观察得出了下面五条信息:① ??????<0 ;② ??+??+??<0 ;③ ??+2??>0 ;④ ???2??+4??>0 ;⑤ ??=
3
2
?? , 你认为其中正确信息的个数有________个. /
18.如图,已知双曲线y=
??
??
(k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=________.
19.若y=(m2-3m)x|m|-4为反比例函数,则m=________.
20.如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(
1
2
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 ?________.(填写正确结论的序号) /
三、解答题(共9题;共60分)
21.已知二次函数 ??=??
(????)
2
,当 ??=2 时有最大值,且此函数的图象经过点 (1,?3) ,求此二次函数的关系式,并指出当 ?? 为何值时, ?? 随 ?? 的增大而增大.
22.如图,直线l⊥x轴于点P,且与反比例函数y1=
??
1
??
(x>0)及y2=
??
2
??
(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,求k1-k2的值.
/
23.有一个周长为40厘米的正方形,从四个角各剪去一个正方形,做成一个无盖盒子.设这个盒子的底面积为y,剪去的正方形的边长为x,求有关y的二次函数.
24.如图,在直角坐标系中,O为坐标原点.已知反比例函数y=
??
??
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
1
2
. (1)求k和m的值; (2)求当x≥1时函数值y的取值范围. /
25.如图所示,在直角坐标系xOy中,一次函数y1=k1x+b(k≠0)的图象与反比例函数
??
2
=
??
2
??
(x>0)的图象交于A(1,4),B(3,m)两点. / (1)试确定上述反比例函数和一次函数的表达式; (2)在第一象限内,x取何值时,一次函数的函数值大于反比例函数的函数值; (3)求△AOB的面积.
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点。 / ⑴求这个二次函数的表达式; ⑵连结PO、PC,在同一平面内把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由; ⑶当点P运动到什么位置时,四边形ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
27.如图,双曲线??=
??
??
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0). / (1)求反比例函数和一次函数的解析式; (2)连接OA、OB,求△AOB的面积; (3)根据图象直接写出在第一象限内反比例函数值大于一次函数值时x的取值范围.
28.如图,直线AB交双曲线 ??=
??
??
于A,B两点,交x轴于点C,且BC=
1
2
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
/
29.宁波某公司经销一种绿茶,每千克成本为 50 元.市场调查发现,在一段时间内,销售量 ?? (千克)随销售单价 ?? (元/千克)的变化而变化,具体关系式为: ??=?2??+240 .设这种绿茶在这段时间内的销售利润为 ?? (元),解答下列问题:
(1)求 ?? 与 ?? 的关系式;
(2)当销售单价 ?? 取何值时,销售利润 ?? 的值最大,最大值为多少?
(3)如果物价部门规定这种绿茶的销售单价不得高于 90 元/千克,公司想要在这段时间内获得 2250 元的销售利润,销售单价应定为多少元?
答案解析部分
一、单选题
1.【答案】A
2.【答案】C
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】C
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】A
二、填空题
11.【答案】-6
12.【答案】a<﹣1
13.【答案】2
14.【答案】y=﹣
3
8
x2+
3
4
x+3
15.【答案】5或13
16.【答案】y=x2﹣
3
2
x
17.【答案】4
18.【答案】2
19.【答案】-3
20.【答案】①③⑤
三、解答题
21.【答案】解:根据题意得y=a(x﹣2)2 , 把(1,﹣3)代入得a=﹣3, 所以二次函数解析式为y=﹣3(x﹣2)2 , 因为抛物线的对称轴为直线x=2,抛物线开口向下, 所以当x<2时,y随x的增大而增大
22.【答案】解:∵反比例函数 ??=
??
1
??
(x>0)及 ??=
??
2
??
(x>0)的图象均在第一象限内,∴
??
1
>0,
??
2
>0
∵AP⊥x轴,∴S△OAP=
1
2
??
1
,S△OBP=
1
2
??
2
,∴S△OAB=S△OAP﹣S△OBP=
1
2
(
??
1
?
??
2
) =2,解得:
??
1
?
??
2
=4
23.【答案】解:根据题意可得:正方形的边长为40÷4=10(厘米), y=(10﹣2x)2=4x2﹣40x+100.
24.【答案】解:(1)∵A(2,m), ∴OB=2,AB=m, ∴S△AOB=
1
2
?OB?AB=
1
2
×2×m=
1
2
, ∴m=
1
2
, ∴点A的坐标为(2,
1
2
), 把A(2,
1
2
)代入y=
??
??
,得k=1; (2)∵当x=1时,y=1, 又∵反比例函数y=
1
??
在x>0时,y随x的增大而减小, ∴当x≥1时,y的取值范围为0<y≤1.
25.【答案】(1)把A(1,4)代入数
??
2
=
??
2
??
(x>0)得:4=
??
2
1
, 解得:k2=4, 即反比例函数的解析式是:y2=
4
??
, 把B(3,m)代入上式得:m=
4
3
, 即B(3,
4
3
), 把A、B的坐标代入y1=k1x+b(k≠0)得:
4=
??
1
+??
4
3
=3
??
1
+??
解得:k=-
4
3
,b=
16
3
, ∴一次函数的解析式是:y1=-
4
3
x+
16
3
; (2)从图象可知:在第一象限内,x取1<x<3时,一次函数的函数值大于反比例函数的函数值; (3)过A作AE⊥ON于E,过B作BF⊥OM于F, / ∵A(1,4),B(3,
4
3
), ∴AE=1,BF=
4
3
, ∵设直线AB(y1=﹣
4
3
x+
16
3
)交y轴于N,交x轴于M, 当x=0时,y=
16
3
, 当y=0时,x=4, 即ON=
16
3
,OM=4, ∴S△AOB=S△NOM﹣S△AON﹣S△BOM =
1
2
×
16
3
×4﹣
1
2
×4×1﹣
1
2
×4×
4
3
=
16
3
.
26.【答案】解:⑴将B、C两点坐标代入得
3??+??=?9
??=?3
解得:
??=?2
??=?3
. 所以二次函数的表示式为:y=x2-2x-3 ⑵存在点P,使四边形POP′C为菱形,设P点坐标为(x,x2-2x-3),PP′交CO于E, 若四边形POP′C是菱形,则有PC=PO,连结PP′,则PE⊥OC于E, ∴OE=EC=
3
2
, ∴y=?
3
2
∴x2-2x-3=?
3
2
, 解得x1=
2+
10
2
,x2=
2?
10
2
,(不合题意,舍去) ∴P点的坐标为(
2+
10
2
,?
3
2
). ⑶过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2-2x-3),易得,直线BC的解析式为y=x-3,则Q点的坐标为(x,x-3) / S四边形ABPC=S△ABC+S△BPQ+S△CPQ=
1
2
AB·OC+
1
2
QP·OF+
1
2
QP·FB =
1
2
AB·OC+
1
2
QP·(OF+FB)
1
2
AB·OC+
1
2
QP·OB =
1
2
×4×3+
1
2
?
??
2
+3??
×3 =?
3
2
???
3
2
2
+
75
8
当??=
3
2
时,四边形ABPC的面积最大 此时P点的坐标为
3
2
,?
15
4
,四边形ABPC的面积的最大值为
75
8
.
27.【答案】解:(1)把A(1,5)代入??=
??
??
得:k=5, ∴反比例函数的解析式是y=
5
??
, 把A、C的坐标代入y=mx+n得:
??+??=5
6??+??=0
, 解得:m=﹣1,n=6, ∴一次函数的解析式是y=﹣x+6; (2)解方程组
??=
5
??
??=???+6
得:
??
1
=1
??
1
=5
,
??
2
=5
??
2
=1
∵A(1,5), ∴B(5,1), ∵C(6,0), ∴OC=6, ∴S△AOB=S△AOC﹣S△BCO=
1
2
×6×5﹣
1
2
×6×1=12; (3)在第一象限内反比例函数值大于一次函数值时x的取值范围是0<x<1或x>6.
28.【答案】解:设B(a,b), ∵点B在函数y= /上, ∴ab=k,且OM=a,BM=b, ∵OM=3MC, ∴MC= /a, ∴S△BOM= /ab= /k,S△BMC= /× /ab= /ab= /k, ∴S△BOC=S△BOM+S△BMC= /k+ /k= /k, ∵BC= /AB,不妨设点O到AC的距离为h, 则 /= /= /= /, ∴S△AOB=2S△BOC= /k, ∴S△AOC=S△AOB+S△BOC= /k+ /k=2k, ∵S△AOC=8. ∴2k=8, ∴k=4
29.【答案】(1)解:由题意可知:y=(x-50)×w=(x-50)×(-2x+240)=-2
??
2
+340x-12000 ∴y 与 x 的关系式为:y=(x-50)×w=(x-50)×(-2x+240)=-2
??
2
+340x-12000 (2)解:由(1)得:y=-2
??
2
+340x-12000 , 配方得:y=-2
???85
2
+2450 ; ∵函数开口向下,且对称轴为x=85, ∴当x=85时,y的值最大,且最大值为2450. (3)解:当y=2250时,可得方程 -2
???85
2
+2450=2250; 解得:
??
1
=75,
??
2
=95 ; 由题意可知:x≤90, ∴
??
2
=95 不合题意,应该舍去。 ∴当销售单价为75元时,可获得销售利润2250元。?????????????????????????????????????????????
一、单选题(共10题;共30分)
1.抛物线y=(x﹣2)2+3的对称轴是(?? )
A.?直线x=2??????????????????????????B.?直线x=3??????????????????????????C.?直线x=﹣2??????????????????????????D.?直线x=﹣3
2.已知反比例函数y=
6
??
,下列各点不在该函数图象上的是(?? )
A.?(2,3)??????????/B.?(﹣2,﹣3)??????????/C.?(-3,-2)? ??????????/D.?? (-1,6)
3.抛物线y=2(x﹣3)2+1的顶点坐标是(? )
A.?(3,1)??????????????????????/B.?(3,﹣1)??????????????????????/C.?(﹣3,1)??????????????????????/D.?(﹣3,﹣1)
4.反比例函数 ??=?
3
??
的图象上有
??
1
(
??
1
,?2),
??
2
(
??
2
,?3) ?两点,则
??
1
与
??
2
的大小关系是(?? )
A.?
??
1
>
??
2
????????????????????????????????/B.?
??
1
=
??
2
????????????????????????????????/C.?
??
1
<
??
2
????????????????????????????????/D.?不确定
5.若反比例函数y=
??
??
的图象位于第二、四象限,则k的取值可能是( )
A.?-1 ???/B.?2 ???/C.?3 ?/D.?4
6.关于函数y=(500﹣10x)(40+x),下列说法不正确的是( )
A.?y是x的二次函数??????????????/B.?二次项系数是﹣10?????????????/C.?一次项是100?????????????/D.?常数项是20000
7.已知正方形ABCD,设AB=x,则正方形的面积y与x之间的函数关系式为( )
A.?y=4x??????????????????????????????????/B.?y=x2??????????????????????????????????/C.?x=
??
4
??????????????????????????????????/D.???=
??
8.若二次函数y=x2-6x+c的图象过A(-1,y1)、B(2,y2)、C(3+
2
,y3)三点,则y1、y2、y3的大小关系正确的是( ??????)
A.?y1>y2>y3??????????????????????/B.?y1>y3>y2??????????????????????/C.?y2>y1>y3??????????????????????/D.?y3>y1>y2
9.(2016?湖北)一次函数y=ax+b和反比例函数y=
??
??
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) /
A.?/????????????/B.?/????????????/C.?/????????????/D.?/
10.(2017?滨州)在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=
1
??
相交于点A、B,且AC+BC=4,则△OAB的面积为(??? )
A.?2
3
+3或2
3
﹣3??????????????????/B.?
2
+1或
2
﹣1??????????????????/C.?2
3
﹣3??????????????????/D.?
2
﹣1
二、填空题(共10题;共30分)
11.二次函数y=x2﹣2x﹣5的最小值是________.
12.如果抛物线y=(a+1)x2﹣4有最高点,那么a的取值范围是________.
13.如图,直线y=
1
2
x与双曲线y=
??
??
在第一象限的交点为A(2,m),则k=________. /
14.经过A(4,0),B(﹣2,0),C(0,3)三点的抛物线解析式是________.
15.二次函数 ??=
??
2
?6??+?? 的图象的顶点与原点的距离为5,则c=________。
16.试写出一个二次函数关系式,使它对应的一元二次方程的一个根为0,另一个根在1到2之间:________.
17.如图所示的二次函数 ??=??
??
2
+????+??(??≠0) 的图象中,观察得出了下面五条信息:① ??????<0 ;② ??+??+??<0 ;③ ??+2??>0 ;④ ???2??+4??>0 ;⑤ ??=
3
2
?? , 你认为其中正确信息的个数有________个. /
18.如图,已知双曲线y=
??
??
(k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=________.
19.若y=(m2-3m)x|m|-4为反比例函数,则m=________.
20.如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(
1
2
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 ?________.(填写正确结论的序号) /
三、解答题(共9题;共60分)
21.已知二次函数 ??=??
(????)
2
,当 ??=2 时有最大值,且此函数的图象经过点 (1,?3) ,求此二次函数的关系式,并指出当 ?? 为何值时, ?? 随 ?? 的增大而增大.
22.如图,直线l⊥x轴于点P,且与反比例函数y1=
??
1
??
(x>0)及y2=
??
2
??
(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,求k1-k2的值.
/
23.有一个周长为40厘米的正方形,从四个角各剪去一个正方形,做成一个无盖盒子.设这个盒子的底面积为y,剪去的正方形的边长为x,求有关y的二次函数.
24.如图,在直角坐标系中,O为坐标原点.已知反比例函数y=
??
??
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
1
2
. (1)求k和m的值; (2)求当x≥1时函数值y的取值范围. /
25.如图所示,在直角坐标系xOy中,一次函数y1=k1x+b(k≠0)的图象与反比例函数
??
2
=
??
2
??
(x>0)的图象交于A(1,4),B(3,m)两点. / (1)试确定上述反比例函数和一次函数的表达式; (2)在第一象限内,x取何值时,一次函数的函数值大于反比例函数的函数值; (3)求△AOB的面积.
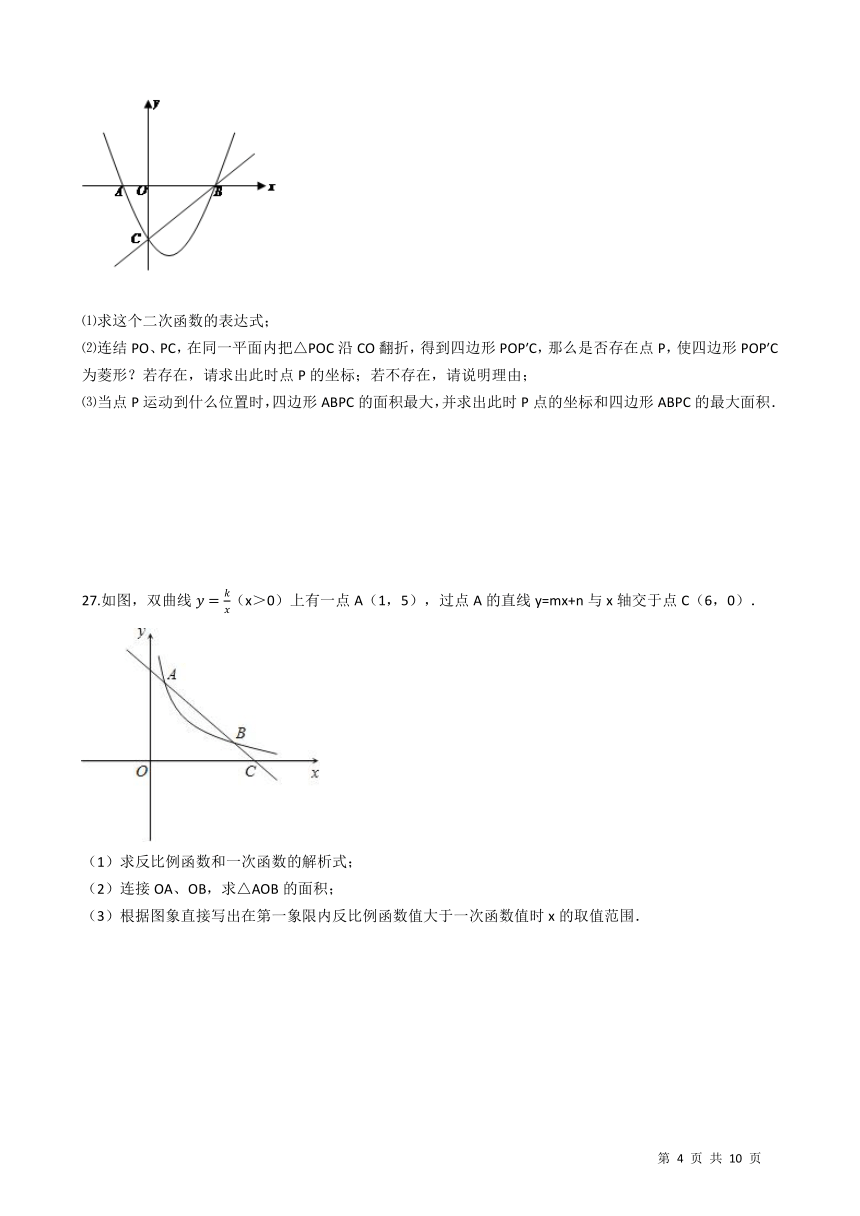
26.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点。 / ⑴求这个二次函数的表达式; ⑵连结PO、PC,在同一平面内把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由; ⑶当点P运动到什么位置时,四边形ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
27.如图,双曲线??=
??
??
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0). / (1)求反比例函数和一次函数的解析式; (2)连接OA、OB,求△AOB的面积; (3)根据图象直接写出在第一象限内反比例函数值大于一次函数值时x的取值范围.
28.如图,直线AB交双曲线 ??=
??
??
于A,B两点,交x轴于点C,且BC=
1
2
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
/
29.宁波某公司经销一种绿茶,每千克成本为 50 元.市场调查发现,在一段时间内,销售量 ?? (千克)随销售单价 ?? (元/千克)的变化而变化,具体关系式为: ??=?2??+240 .设这种绿茶在这段时间内的销售利润为 ?? (元),解答下列问题:
(1)求 ?? 与 ?? 的关系式;
(2)当销售单价 ?? 取何值时,销售利润 ?? 的值最大,最大值为多少?
(3)如果物价部门规定这种绿茶的销售单价不得高于 90 元/千克,公司想要在这段时间内获得 2250 元的销售利润,销售单价应定为多少元?
答案解析部分
一、单选题
1.【答案】A
2.【答案】C
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】C
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】A
二、填空题
11.【答案】-6
12.【答案】a<﹣1
13.【答案】2
14.【答案】y=﹣
3
8
x2+
3
4
x+3
15.【答案】5或13
16.【答案】y=x2﹣
3
2
x
17.【答案】4
18.【答案】2
19.【答案】-3
20.【答案】①③⑤
三、解答题
21.【答案】解:根据题意得y=a(x﹣2)2 , 把(1,﹣3)代入得a=﹣3, 所以二次函数解析式为y=﹣3(x﹣2)2 , 因为抛物线的对称轴为直线x=2,抛物线开口向下, 所以当x<2时,y随x的增大而增大
22.【答案】解:∵反比例函数 ??=
??
1
??
(x>0)及 ??=
??
2
??
(x>0)的图象均在第一象限内,∴
??
1
>0,
??
2
>0
∵AP⊥x轴,∴S△OAP=
1
2
??
1
,S△OBP=
1
2
??
2
,∴S△OAB=S△OAP﹣S△OBP=
1
2
(
??
1
?
??
2
) =2,解得:
??
1
?
??
2
=4
23.【答案】解:根据题意可得:正方形的边长为40÷4=10(厘米), y=(10﹣2x)2=4x2﹣40x+100.
24.【答案】解:(1)∵A(2,m), ∴OB=2,AB=m, ∴S△AOB=
1
2
?OB?AB=
1
2
×2×m=
1
2
, ∴m=
1
2
, ∴点A的坐标为(2,
1
2
), 把A(2,
1
2
)代入y=
??
??
,得k=1; (2)∵当x=1时,y=1, 又∵反比例函数y=
1
??
在x>0时,y随x的增大而减小, ∴当x≥1时,y的取值范围为0<y≤1.
25.【答案】(1)把A(1,4)代入数
??
2
=
??
2
??
(x>0)得:4=
??
2
1
, 解得:k2=4, 即反比例函数的解析式是:y2=
4
??
, 把B(3,m)代入上式得:m=
4
3
, 即B(3,
4
3
), 把A、B的坐标代入y1=k1x+b(k≠0)得:
4=
??
1
+??
4
3
=3
??
1
+??
解得:k=-
4
3
,b=
16
3
, ∴一次函数的解析式是:y1=-
4
3
x+
16
3
; (2)从图象可知:在第一象限内,x取1<x<3时,一次函数的函数值大于反比例函数的函数值; (3)过A作AE⊥ON于E,过B作BF⊥OM于F, / ∵A(1,4),B(3,
4
3
), ∴AE=1,BF=
4
3
, ∵设直线AB(y1=﹣
4
3
x+
16
3
)交y轴于N,交x轴于M, 当x=0时,y=
16
3
, 当y=0时,x=4, 即ON=
16
3
,OM=4, ∴S△AOB=S△NOM﹣S△AON﹣S△BOM =
1
2
×
16
3
×4﹣
1
2
×4×1﹣
1
2
×4×
4
3
=
16
3
.
26.【答案】解:⑴将B、C两点坐标代入得
3??+??=?9
??=?3
解得:
??=?2
??=?3
. 所以二次函数的表示式为:y=x2-2x-3 ⑵存在点P,使四边形POP′C为菱形,设P点坐标为(x,x2-2x-3),PP′交CO于E, 若四边形POP′C是菱形,则有PC=PO,连结PP′,则PE⊥OC于E, ∴OE=EC=
3
2
, ∴y=?
3
2
∴x2-2x-3=?
3
2
, 解得x1=
2+
10
2
,x2=
2?
10
2
,(不合题意,舍去) ∴P点的坐标为(
2+
10
2
,?
3
2
). ⑶过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(x,x2-2x-3),易得,直线BC的解析式为y=x-3,则Q点的坐标为(x,x-3) / S四边形ABPC=S△ABC+S△BPQ+S△CPQ=
1
2
AB·OC+
1
2
QP·OF+
1
2
QP·FB =
1
2
AB·OC+
1
2
QP·(OF+FB)
1
2
AB·OC+
1
2
QP·OB =
1
2
×4×3+
1
2
?
??
2
+3??
×3 =?
3
2
???
3
2
2
+
75
8
当??=
3
2
时,四边形ABPC的面积最大 此时P点的坐标为
3
2
,?
15
4
,四边形ABPC的面积的最大值为
75
8
.
27.【答案】解:(1)把A(1,5)代入??=
??
??
得:k=5, ∴反比例函数的解析式是y=
5
??
, 把A、C的坐标代入y=mx+n得:
??+??=5
6??+??=0
, 解得:m=﹣1,n=6, ∴一次函数的解析式是y=﹣x+6; (2)解方程组
??=
5
??
??=???+6
得:
??
1
=1
??
1
=5
,
??
2
=5
??
2
=1
∵A(1,5), ∴B(5,1), ∵C(6,0), ∴OC=6, ∴S△AOB=S△AOC﹣S△BCO=
1
2
×6×5﹣
1
2
×6×1=12; (3)在第一象限内反比例函数值大于一次函数值时x的取值范围是0<x<1或x>6.
28.【答案】解:设B(a,b), ∵点B在函数y= /上, ∴ab=k,且OM=a,BM=b, ∵OM=3MC, ∴MC= /a, ∴S△BOM= /ab= /k,S△BMC= /× /ab= /ab= /k, ∴S△BOC=S△BOM+S△BMC= /k+ /k= /k, ∵BC= /AB,不妨设点O到AC的距离为h, 则 /= /= /= /, ∴S△AOB=2S△BOC= /k, ∴S△AOC=S△AOB+S△BOC= /k+ /k=2k, ∵S△AOC=8. ∴2k=8, ∴k=4
29.【答案】(1)解:由题意可知:y=(x-50)×w=(x-50)×(-2x+240)=-2
??
2
+340x-12000 ∴y 与 x 的关系式为:y=(x-50)×w=(x-50)×(-2x+240)=-2
??
2
+340x-12000 (2)解:由(1)得:y=-2
??
2
+340x-12000 , 配方得:y=-2
???85
2
+2450 ; ∵函数开口向下,且对称轴为x=85, ∴当x=85时,y的值最大,且最大值为2450. (3)解:当y=2250时,可得方程 -2
???85
2
+2450=2250; 解得:
??
1
=75,
??
2
=95 ; 由题意可知:x≤90, ∴
??
2
=95 不合题意,应该舍去。 ∴当销售单价为75元时,可获得销售利润2250元。?????????????????????????????????????????????
