第五章几何证明初步练习题（含答案）

八年级数学几何证明初步单元测试
一、选择题（本大题共6小题，每小题2分，满分12分）
1.下列条件不能推出两个直角三角形全等的是--------------------------（ ）
（A）两条直角边对应相等 （B）一个锐角和一条直角边对应相等
(C)一条直角边和斜边对应相等 (D)两个锐角对应相等
2.下列命题中, 逆命题正确的是--------------------------------------（ ）
(A)对顶角相等 (B)直角三角形两锐角互余
(C)全等三角形面积相等 (D)全等三角形对应角相等
3.如图,⊿是等腰直角三角形,点在边上,且,则是----- （ ）
（A） （B） （C） （D）
4. 在直角三角形中，若有一个角等于，那么三角形三边的比为------- （ ）
（A）:: （B）:: （C）:: （D）::
5．下列各组数中不能作为直角三角形的三边长的是-------------------- （ ）
（A）、、 （B）、、 （C） 、、（D）、、
6. 如图，是⊿的中线，，将⊿沿直线翻折，点落在点的位置上，如果，求的长为---------（ ）
（A） （B）（ C） （D）
二、填空题：（本大题共12小题，每小题3分，满分36分）
7.命题“等腰三角形两腰相等”的逆命题是____________ ___．
8.到定点的距离为的点的轨迹是____________ ____________．
9.如图，已知， 是的中垂线，则是__________．
10.如图，已知点是的角平分线上的点，,如果，那么点到的距离是 .
11.若直角三角形的两个锐角的比是，则这个直角三角形的较大的锐角是 ___________度．
12.若⊿的两条直角边分别为1和2，则斜边为___________．
13．在⊿中， ，，，则 .
14．已知点，,则线段的长为_____________．
15．如果一个三角形的三条边长分别为，那么这个三角形的面积为_____________．
16．如图，以直角三角形三边向外作正方形，三个正方形的面积分别是、、，且，,则＝_________．
17.如图，,请你再添加一个条件： ，使 .
18. 等腰三角形腰上的高是腰长的一半，那么它的顶角等于_______.
三、解答题：（共4小题，第19，20题每题5分，第21，22题每题6分，满分22分）
19. 如图，求作一点，使，并且到两边的距离相等．
20. 如图，已知，.求证：.
21. 已知直角坐标平面的两点分别为，设点在轴上，且，求点的坐标．
22.已知⊿的三个顶点分别是、、，试判断⊿的形状.
四、解答题：（共4小题，第23、24题每题7分，第25、26题每题8分，满分30分）
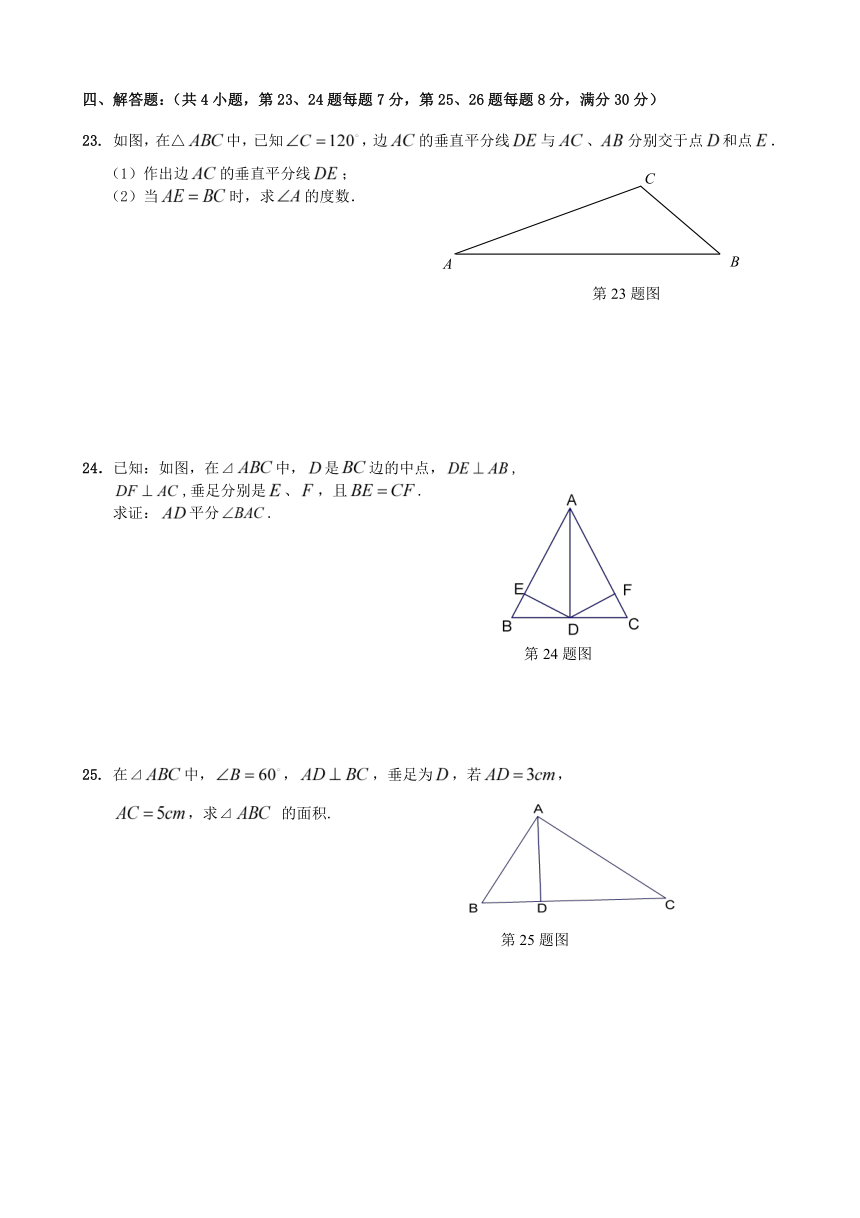
23. 如图，在△中，已知，边的垂直平分线与、分别交于点和点．
（1） 作出边的垂直平分线；
（2） 当时，求的度数．
24．已知：如图，在⊿中，是边的中点，,
,垂足分别是、，且.
求证：平分.
25. 在⊿中，，，垂足为，若，
，求⊿ 的面积.
26．已知：如图，在⊿中，，，，点、、 分别在边、、上（点、与⊿顶点不重合），平分，，垂足为．
（1） 求证：；
（2） 设，，求与之间的函数解析式，并写出定义域；
（3） 当⊿是直角三角形时，求出的长．
参考答案
一、选择题（本大题共6小题，每小题2分，满分12分）
1. 2. 3. 4. 5. 6.
二、填空题（本大题共12小题，每小题3分，满分36分）
7.两条边相等的三角形是等腰三角形 8.以点为圆心，为半径的圆
9. 10. 11. 12. 13. 14. 15. 16.
17.，，，四个答案任选一个
18.或
三、解答题（本大题共4小题，第19，20题每题5分，第21，22题每题6分，满分22分）
19.作图略 （中垂线2分，角平分线2分，结论1分）
20.证明：联结 . .(2分)
(2分)..（1分）
21. 解：点在轴上，可设点的坐标为， （1分）得
,（1分）
（两点距离公式）.（1分）
（已知）,, 即 =.（1分）
解得 . （1分） 的坐标为.（1分）
22. 解：，（1分）
， （1分）
（两点距离公式）. （1分）
得. （1分）
, .
得（勾股定理的逆定理）. （1分）
⊿是等腰直角三角形. （1分）
四、解答题（本大题共4小题，第23、24题每题7分，第25、26题每题8分，满分30分）
23. 证明：（1）作出垂直平分线．（2分）
（2）联结 ． ∵垂直平分，∴ ．（1分）
∵，∴．（1分）
设，则．∴．（1分）
∵，∴.（1分）
∴，即．（1分）
24.，.（1分）
是的中点，.（1分）
在⊿和⊿中，
（）. (2分)
.（1分）
(已知)，平分（在一个角的内部且到角的两边距离相等的点，在这个角的角平分线上）. (2分)
25. ，.（1分）
,.（1分） .（1分）
设=x，则．，，（1分）
求得.（1分） 同理可得.（1分）
.（1分） .（1分）
26 .（1）证明：∵，∴.
在△和△中，
∴△≌△ (A.S.A）. （1分）
∴．（1分）
（2）解：在△中，∵，，∴. （1分）
∵,∴,∴.（1分）
函数定义域为. （1分）
（3）解：∵,，∴垂直平分. ∴.
∵△是直角三角形,∴.∴.
又∵,∴，
∴，∴. （1分）
设,则, .（1分）
∵,.（1分）
第3题图
第6题图
第9题图
第10题图
第16题图
第17题图
第20题图
B
C
A
第23题图
第24题图
第25题图
A
C
B
D
备用图
第26题图
A
C
H
F
E
D
B