第七章一元一次方程复习学案(无答案)
图片预览



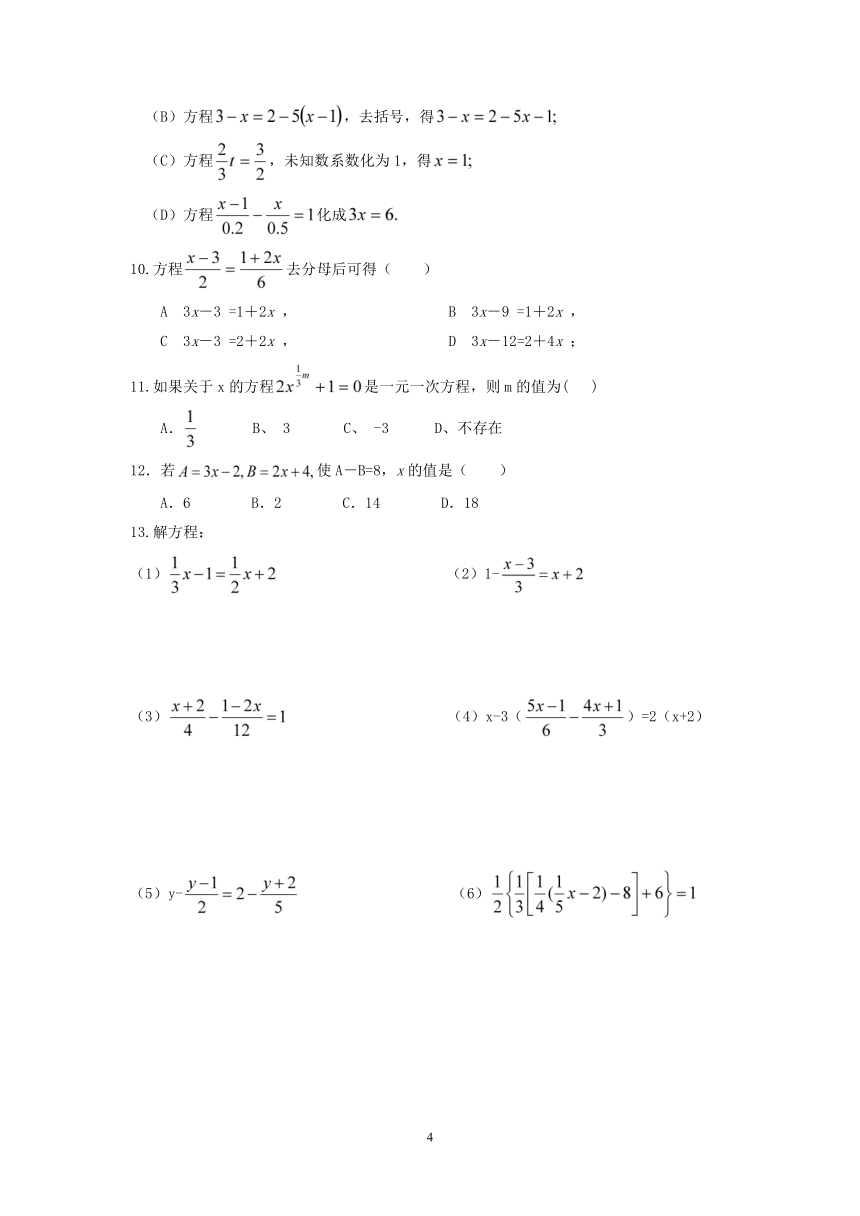
文档简介
一元一次方程复习教案
考点1.一元一次方程的有关概念
(1)一元一次方程:只含有一个未知数,并且未知数的次数是1,系数不等于0,这样的方程叫做一元一次方程.
(2)一元一次方程的标准形式是:
考点2.等式的基本性质
(1)等式的两边都加上或减去 或 ,所得的结果仍是等式.
(2)等式的两边都乘以 或都除以 ,所得的结果仍是等式.
考点3.解一元一次方程的基本步骤:
变形步骤
具 体 方 法
变 形 根 据
注 意 事 项
去分母
方程两边都乘以各个分母的最小公倍数
等式性质2
1.不能漏乘不含分母的项;
2.分数线起到括号作用,去掉分母后,如果分子是多项式,则要加括号
去括号
先去小括号,再去中括号,最后去大括号
乘法分配律、去括号法则
1.分配律应满足分配到每一项
2.注意符号,特别是去掉括号
移 项
把含有未知数的项移到方程的一边,不含有未知数的项移到另一边
等式性质1
1.移项要变号;
2.一般把含有未知数的项移到方程左边,其余项移到右边
合并同
类 项
把方程中的同类项分别合并,化成“”的形式()
合并同类项法则
合并同类项时,把同类项的系数相加,字母与字母的指数不变
未知数的系数化成“1”
方程两边同除以未知数的系数,得
等式性质2
分子、分母不能颠倒
【典型例题】
例1.下列方程是一元一次方程的有哪些?
x+2y=9 x2-3x=1
2x=1 3x–5 3+7=10 x2+x=1
例2. 用适当的数或整式填空,使得结果仍是等式,并说明是根据等式的哪条性质,通过怎样变形得到的.
(1)如果
(2)如果;
(3)如果
(4)如果
例3.解方程
.
3. 4.
6.
例4.解方程
1. 2.
例5.取何值时,代数式 与 的值相等.
例6.已知方程的解与方程的解相同,求m的值.
例7. 已知是关于x的方程 的解,求的值.
例8. 若对于任意的两个有理数m, n都有m※n=,解方程3x※4=2.
跟踪练习
1.若ax+b=0为一元一次方程,则__________.
2.当 时,关于字母x的方程是一元一次方程.
3.若9ax b7 与 – 7a 3x–4 b 7是同类项,则x= .
4.如果,则的值是 .
5.当___时,代数式与的值互为相反数.
6.已知是关于x的一元一次方程,则m= .
7.已知是方程的根,则的值是( )
A. 8 B. -8 C. 0 D. 2
8.如果a、b互为相反数,(a≠0),则ax+b=0的根为( )
A.1 B.-1 C.-1或1 D.任意数
9.下列方程变形中,正确的是( )
(A)方程,移项,得
(B)方程,去括号,得
(C)方程,未知数系数化为1,得
(D)方程化成
10.方程去分母后可得( )
A 3x-3 =1+2x , B 3x-9 =1+2x ,
C 3x-3 =2+2x , D 3x-12=2+4x ;
11.如果关于x的方程是一元一次方程,则m的值为( )
A. B、 3 C、 -3 D、不存在
12.若使A-B=8,x的值是( )
A.6 B.2 C.14 D.18
13.解方程:
(1) (2)1-
(3) (4)x-3()=2(x+2)
(5)y- (6)
提高练习
考点4:用方程解决问题的一般步骤:
二、典型例题
例1 某果品公司需将一批水果从A市运到B市销售,现有3家运输公司提供服务信息如下:
运输单位
运输费用(元/千米)
包装与装卸费用(元)
甲公司
6
1500
乙公司
8
1000
丙公司
10
800
根据以上信息测算,乙、丙两家公司分别经办运输的包装与装卸及运输费用的总和恰好是甲公司的2倍,请问A、B两市的距离是多少?
例2 某个企业存入A、B两种不同性质的存款共20万元,A种存款的年利率为5.5%,B种存款的年利率为4.5%,上缴国家的利息税为20%,该企业一年可获得税后利息收入7600元,求A、B两种存款各多少万元?
三、当堂训练
1、一件商品按成本价提高20%标价,然后打九折出售,售价为275元,这件商品的成本价是多少元?
2、一个两位数,十位上的数字是个位上数字的2倍,如果把这个数的两个数位上的数字交换位置,所得的两位数比原数小36,求原来的两位数。
3、某工地派96人去挖土和运土,如果平均每人每天挖土5m3或运土3m3,那么应怎样分配挖土和运土人数,使挖出的土刚好能及时运走?
4、某种出租车的收费标准是:起步价5元(即行驶距离不超过3km,都需付5元车费),超过3km,每增加0.5km,加收0.9元(不足0.5km按0.5km计)。某人乘坐这种出租车从甲地到乙地共支付车费19.4元,问此人从甲地到乙地经过的路程最远可能是多少千米?
5、甲、乙两人在400米环行跑道上练竞走,乙每分钟走80米,甲的速度是乙的速度的1倍,现甲在乙前面100米,问多少分钟后两人可首次相遇?
四、课后作业
1、一条轮船在A、B两港间航行,船在静水中的速度为10千米/时,水流速度为
1千米/时,若顺水航行时间比逆水航行时间少用4小时,求两港间的距离?
2、甲种商品每件的进价为400元,现在按标价560元的8折出售;乙种商品每件的进价为600元。现在按标价1100元的六折出售,相比较哪种商品的利润率高些?
3、课外数学小组的女同学原来占全组人数的,后来又有4个女同学加入,就占全组人数的,问课外数学小组原来有多少个同学?
某车间有21名工人生产螺栓和螺母,每人每小时能生产螺栓12个或螺母18个,要使每小时生产的螺栓和螺母可按1:2配套,应分别安排多少人生产螺栓和螺母?
5、用两架掘土机掘土,第一架掘土机比第二架掘土机每小时多掘土40 m3, 第一架工作16小时,第二架工作24小时,共掘土8640 m3,问每架掘土机每小时可以掘土多少 m3?
6、甲、乙、丙三个工厂共同筹办一所厂办学校,所出经费不同,其中甲厂出总数的,乙厂出甲丙两厂和的,已知丙厂出了16000元.问这所厂办学校总经费是多少,甲乙两厂各出了多少元?
7、一条山路,从山下到山顶,走了1小时还差1km,从山顶到山下,用50分钟可以走完.已知下山速度是上山速度的1.5倍,问下山速度和上山速度各是多少,单程山路有多少km.
8、某车间在计划时间内加工一批零件,若每天生产40个,则差20个而不能完成任务;若每天生产50个,则可提前1天完成任务,且超额完成10个。问这批零件有多少个?计划多少天完成?
考点1.一元一次方程的有关概念
(1)一元一次方程:只含有一个未知数,并且未知数的次数是1,系数不等于0,这样的方程叫做一元一次方程.
(2)一元一次方程的标准形式是:
考点2.等式的基本性质
(1)等式的两边都加上或减去 或 ,所得的结果仍是等式.
(2)等式的两边都乘以 或都除以 ,所得的结果仍是等式.
考点3.解一元一次方程的基本步骤:
变形步骤
具 体 方 法
变 形 根 据
注 意 事 项
去分母
方程两边都乘以各个分母的最小公倍数
等式性质2
1.不能漏乘不含分母的项;
2.分数线起到括号作用,去掉分母后,如果分子是多项式,则要加括号
去括号
先去小括号,再去中括号,最后去大括号
乘法分配律、去括号法则
1.分配律应满足分配到每一项
2.注意符号,特别是去掉括号
移 项
把含有未知数的项移到方程的一边,不含有未知数的项移到另一边
等式性质1
1.移项要变号;
2.一般把含有未知数的项移到方程左边,其余项移到右边
合并同
类 项
把方程中的同类项分别合并,化成“”的形式()
合并同类项法则
合并同类项时,把同类项的系数相加,字母与字母的指数不变
未知数的系数化成“1”
方程两边同除以未知数的系数,得
等式性质2
分子、分母不能颠倒
【典型例题】
例1.下列方程是一元一次方程的有哪些?
x+2y=9 x2-3x=1
2x=1 3x–5 3+7=10 x2+x=1
例2. 用适当的数或整式填空,使得结果仍是等式,并说明是根据等式的哪条性质,通过怎样变形得到的.
(1)如果
(2)如果;
(3)如果
(4)如果
例3.解方程
.
3. 4.
6.
例4.解方程
1. 2.
例5.取何值时,代数式 与 的值相等.
例6.已知方程的解与方程的解相同,求m的值.
例7. 已知是关于x的方程 的解,求的值.
例8. 若对于任意的两个有理数m, n都有m※n=,解方程3x※4=2.
跟踪练习
1.若ax+b=0为一元一次方程,则__________.
2.当 时,关于字母x的方程是一元一次方程.
3.若9ax b7 与 – 7a 3x–4 b 7是同类项,则x= .
4.如果,则的值是 .
5.当___时,代数式与的值互为相反数.
6.已知是关于x的一元一次方程,则m= .
7.已知是方程的根,则的值是( )
A. 8 B. -8 C. 0 D. 2
8.如果a、b互为相反数,(a≠0),则ax+b=0的根为( )
A.1 B.-1 C.-1或1 D.任意数
9.下列方程变形中,正确的是( )
(A)方程,移项,得
(B)方程,去括号,得
(C)方程,未知数系数化为1,得
(D)方程化成
10.方程去分母后可得( )
A 3x-3 =1+2x , B 3x-9 =1+2x ,
C 3x-3 =2+2x , D 3x-12=2+4x ;
11.如果关于x的方程是一元一次方程,则m的值为( )
A. B、 3 C、 -3 D、不存在
12.若使A-B=8,x的值是( )
A.6 B.2 C.14 D.18
13.解方程:
(1) (2)1-
(3) (4)x-3()=2(x+2)
(5)y- (6)
提高练习
考点4:用方程解决问题的一般步骤:
二、典型例题
例1 某果品公司需将一批水果从A市运到B市销售,现有3家运输公司提供服务信息如下:
运输单位
运输费用(元/千米)
包装与装卸费用(元)
甲公司
6
1500
乙公司
8
1000
丙公司
10
800
根据以上信息测算,乙、丙两家公司分别经办运输的包装与装卸及运输费用的总和恰好是甲公司的2倍,请问A、B两市的距离是多少?
例2 某个企业存入A、B两种不同性质的存款共20万元,A种存款的年利率为5.5%,B种存款的年利率为4.5%,上缴国家的利息税为20%,该企业一年可获得税后利息收入7600元,求A、B两种存款各多少万元?
三、当堂训练
1、一件商品按成本价提高20%标价,然后打九折出售,售价为275元,这件商品的成本价是多少元?
2、一个两位数,十位上的数字是个位上数字的2倍,如果把这个数的两个数位上的数字交换位置,所得的两位数比原数小36,求原来的两位数。
3、某工地派96人去挖土和运土,如果平均每人每天挖土5m3或运土3m3,那么应怎样分配挖土和运土人数,使挖出的土刚好能及时运走?
4、某种出租车的收费标准是:起步价5元(即行驶距离不超过3km,都需付5元车费),超过3km,每增加0.5km,加收0.9元(不足0.5km按0.5km计)。某人乘坐这种出租车从甲地到乙地共支付车费19.4元,问此人从甲地到乙地经过的路程最远可能是多少千米?
5、甲、乙两人在400米环行跑道上练竞走,乙每分钟走80米,甲的速度是乙的速度的1倍,现甲在乙前面100米,问多少分钟后两人可首次相遇?
四、课后作业
1、一条轮船在A、B两港间航行,船在静水中的速度为10千米/时,水流速度为
1千米/时,若顺水航行时间比逆水航行时间少用4小时,求两港间的距离?
2、甲种商品每件的进价为400元,现在按标价560元的8折出售;乙种商品每件的进价为600元。现在按标价1100元的六折出售,相比较哪种商品的利润率高些?
3、课外数学小组的女同学原来占全组人数的,后来又有4个女同学加入,就占全组人数的,问课外数学小组原来有多少个同学?
某车间有21名工人生产螺栓和螺母,每人每小时能生产螺栓12个或螺母18个,要使每小时生产的螺栓和螺母可按1:2配套,应分别安排多少人生产螺栓和螺母?
5、用两架掘土机掘土,第一架掘土机比第二架掘土机每小时多掘土40 m3, 第一架工作16小时,第二架工作24小时,共掘土8640 m3,问每架掘土机每小时可以掘土多少 m3?
6、甲、乙、丙三个工厂共同筹办一所厂办学校,所出经费不同,其中甲厂出总数的,乙厂出甲丙两厂和的,已知丙厂出了16000元.问这所厂办学校总经费是多少,甲乙两厂各出了多少元?
7、一条山路,从山下到山顶,走了1小时还差1km,从山顶到山下,用50分钟可以走完.已知下山速度是上山速度的1.5倍,问下山速度和上山速度各是多少,单程山路有多少km.
8、某车间在计划时间内加工一批零件,若每天生产40个,则差20个而不能完成任务;若每天生产50个,则可提前1天完成任务,且超额完成10个。问这批零件有多少个?计划多少天完成?
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
