沪科版九年级数学下期末综合检测复习试卷(含答案)
文档属性
| 名称 | 沪科版九年级数学下期末综合检测复习试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-03 00:00:00 | ||
图片预览



文档简介
期末专题复习:沪科版九年级数学下册期末综合检测试卷
一、单选题(共10题;共30分)
1.如图,点A,B,C均在⊙O上,若∠A=66°,则∠OCB的度数是( ??) /
A.?24°???????????????????????????????????????B.?28°???????????????????????????????????????C.?33°???????????????????????????????????????D.?48°
2.同时抛掷两枚均匀的硬币,落地后两枚硬币都是正面朝上的概率是(????? )
A.?1??????????????????????????????????????????/B.?
1
2
??????????????????????????????????????????/C.?
1
3
??????????????????????????????????????????/D.?
1
4
3.与如图所示的三视图对应的几何体是(?? ) /
A.?/???????????????????????????B.?/???????????????????????????C.?/???????????????????????????D.?/
4.下列图形中既是中心对称图形又是轴对称图形的是(???)
A.?/???????????????????????????B.?/???????????????????????????C.?/???????????????????????????D.?/
5.如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为(??? ) /
A.?
14
3
π﹣6?????????????????????????????/B.?
25
9
π?????????????????????????????/C.?
33
8
π﹣3?????????????????????????????/D.?
33
+π
6.如图,现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( ?? ? ) /
A.?4cm?????????????????????????????????????B.?3cm?????????????????????????????????????C.?2cm?????????????????????????????????????D.?1cm
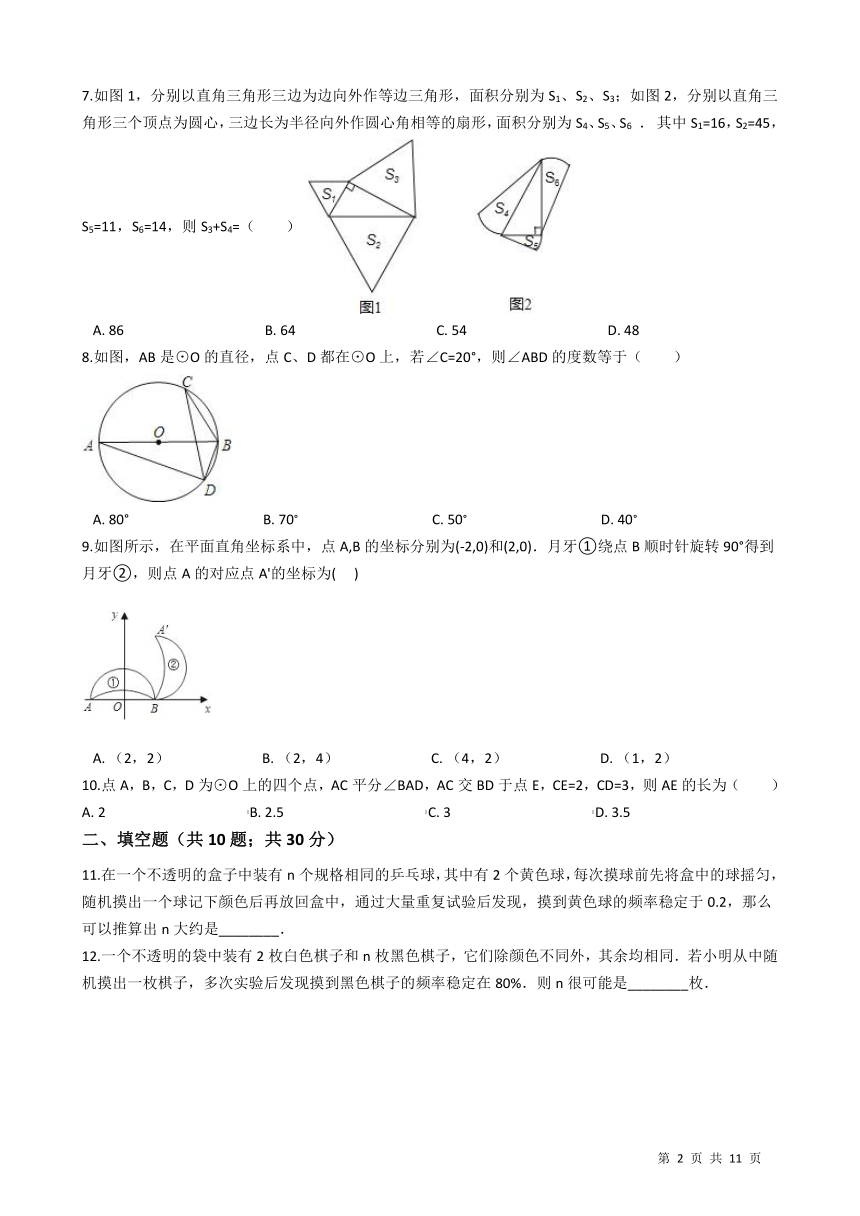
7.如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6 . 其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( ) /
A.?86?????????????????????????????????????????B.?64?????????????????????????????????????????C.?54?????????????????????????????????????????D.?48
8.如图,AB是⊙O的直径,点C、D都在⊙O上,若∠C=20°,则∠ABD的度数等于( ) /?
A.?80°???????????????????????????????????????B.?70°???????????????????????????????????????C.?50°???????????????????????????????????????D.?40°
9.如图所示,在平面直角坐标系中,点A,B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A'的坐标为(??? ) /
A.?(2,2)???????????????????????????B.?(2,4)???????????????????????????C.?(4,2)???????????????????????????D.?(1,2)
10.点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=2,CD=3,则AE的长为( ) A.?2?????????????????????????????????????????/B.?2.5?????????????????????????????????????????/C.?3?????????????????????????????????????????/D.?3.5
二、填空题(共10题;共30分)
11.在一个不透明的盒子中装有n个规格相同的乒乓球,其中有2个黄色球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到黄色球的频率稳定于0.2,那么可以推算出n大约是________.
12.一个不透明的袋中装有2枚白色棋子和n枚黑色棋子,它们除颜色不同外,其余均相同.若小明从中随机摸出一枚棋子,多次实验后发现摸到黑色棋子的频率稳定在80%.则n很可能是________枚.
13.如图,在⊙O中,
????
∧
=
????
∧
,∠C=75°,则∠A=________?°. /
14.(2015?曲靖)一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗,每次随机摸出一颗珠子,放回摇匀后再摸,通过多次试验发现摸到白珠子的频率稳定在0.3左右,则盒子中黑珠子可能有________?颗.
15.如图(右上),在△ABC中,∠ABC=24°,以AB为直径的⊙O交BC于点D,交CA 的延长线于点E,若点E在BD的垂直平分线上,则∠C的度数为________.
/
16.? 3.12 日植树节,老师想从甲、乙、丙、丁4名同学中挑选2名同学代表班级去参加学校组织的植树活动,恰好选中甲和乙去参加的概率是________.
17.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于________?. /
18.如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________?. /
19.在一个不透明的袋子中,有3个白球和1个红球,它们只有颜色上的区别,从袋子中随机摸出一个球记下颜色放回,再随机地摸出一个球,则两次都摸到白球的概率为________ .
20.如图,在菱形ABCD中,tanA=
3
,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=
3
4
CG2;其中正确结论的序号为________. /
三、解答题(共9题;共60分)
21.如图是由6个正方体组成的几何体,请分别画出从正面、左面、上面看到的这个几何体的形状图。 /
22.小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由. /
23.如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连接OE、AC,且∠P=∠E,∠POE=2∠CAB. /
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,PB=9,求⊙O的半径及tan∠P的值.
24.一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位上的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数.试问:按这种方法能组成哪些两位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
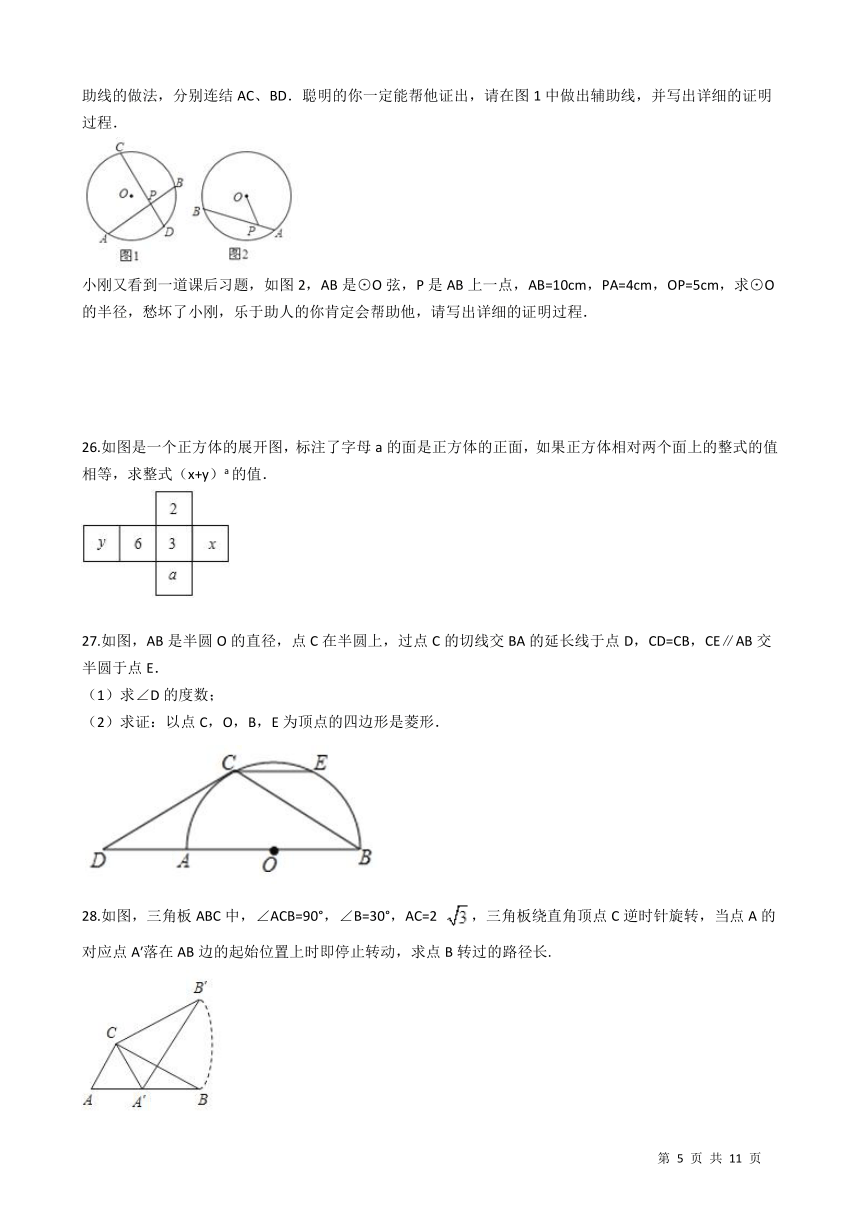
25.九年级学生小刚是一个喜欢看书的好学生,他在学习完第二十四章圆后,在家里突然看到爸爸的初中数学书上居然还有一个相交弦定理(圆内的两条相交弦,被交点分成的两条线段长的积相等),非常好奇,仔细阅读原来就是:PA?PB=PC?PD,小刚很想知道是如何证明的,可异证明部分污损看不清了,只看到辅助线的做法,分别连结AC、BD.聪明的你一定能帮他证出,请在图1中做出辅助线,并写出详细的证明过程. / 小刚又看到一道课后习题,如图2,AB是⊙O弦,P是AB上一点,AB=10cm,PA=4cm,OP=5cm,求⊙O的半径,愁坏了小刚,乐于助人的你肯定会帮助他,请写出详细的证明过程.
26.如图是一个正方体的展开图,标注了字母a的面是正方体的正面,如果正方体相对两个面上的整式的值相等,求整式(x+y)a的值.
/
27.如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E. (1)求∠D的度数; (2)求证:以点C,O,B,E为顶点的四边形是菱形. ?/
28.如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2 /,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,求点B转过的路径长. /
29.学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票.班长由王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动.你认为这个方法公平吗?请画树状图或列表,并说明理由. /
答案解析部分
一、单选题
1.【答案】A
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】B
10.【答案】B
二、填空题
11.【答案】10
12.【答案】8
13.【答案】30
14.【答案】14
15.【答案】33°
16.【答案】
1
6
17.【答案】40°
18.【答案】4
19.【答案】
9
16
20.【答案】(1)(3)(4)
三、解答题
21.【答案】解:正面看到的形状为: / 左面看到的形状为: / 正面看到的形状为: /
22.【答案】解:这个游戏规则对双方公平.理由如下: 画树状图为: / 共有9种等可能的结果数,其中摸出的两张卡片的正面数字之积小于10的结果数为4;摸出的两张卡片的正面数字之积超过10的结果数为4, 所以小明获胜的概率=
4
9
,小亮获胜的概率=
4
9
. 所以这个游戏规则对双方公平
23.【答案】(1)证明:连接OC, ∴∠COB=2∠CAB, 又∠POE=2∠CAB. ∴∠COD=∠EOD, 则弧BC=弧BE, 即CE⊥AB; / (2)证明:∵CE⊥AB,∠P=∠E, ∴∠P+∠PCD=∠E+∠PCD=90°, 又∠OCD=∠E, ∴∠OCD+∠PCD=∠PCO=90°, ∴PC是⊙O的切线; (3)解:设⊙O的半径为r,OD=x,则BD=2x,r=3x, ∵CD⊥OP,OC⊥PC, ∴Rt△OCD∽Rt△OPC, ∴OC2=OD?OP,即(3x)2=x?(3x+9), 解之得x=
3
2
, ∴⊙O的半径r=
9
2
, 在Rt△OCP中, PC=
??
??
2
???
??
2
=
(
9
2
+9)
2
+
(
9
2
)
2
=9
2
, tan∠P=
????
????
=
2
4
.
24.【答案】解:根据题意列表如下: / 十位上则十位上的数字和个位上的数字之和为9的两位数有45和54,所以其概率为:2÷9=
2
9
.
25.【答案】解:(1)圆的两条弦相交,这两条弦被交点分成的两条线段的积相等. 已知,如图1,⊙O的两弦AB、CD相交于E, 求证:AP?BP=CP?DP. 证明如下: 连结AC,BD,如图1, ∵∠C=∠B,∠A=∠D, ∴△APC∽△DPB, ∴AP:DP=CP:BP, ∴AP?BP=CP?DP; 所以两条弦相交,被交点分成的两条线段的积相等. (2)过P作直径CD,如图2, ∵AB=10,PA=4,OP=5, ∴PB=10﹣4=6,PC=OC﹣OP=R﹣5,PD=OD+OP=R+5, 由(1)中结论得,PA?PB=PC?PD, ∴4×6=(R﹣5)×(R+5), 解得R=7(R=﹣7舍去). 所以⊙O的半径R=7. /
26.【答案】81
解答:根据题意得:y=3,x=6,a=2,
故(x+y)a
=(x+y)2
=92
=81.
27.【答案】(1)解:连接AC, ∵CD是⊙O的切线, ∴∠ACD=∠ABC, ∵AB是直径, ∴∠ACB=90°, ∵CD=CB, ∴∠D=∠ABC, ∴∠D=∠ACD=∠ABC, ∵∠D+∠ACD+∠ABC+∠ACB=90°, ∴∠D=30°; (2)证明:连接OC、BE, ∵∠D=∠ACD=30°, ∴∠CAB=60°, ∵OA=OC, ∴△AOC是等边三角形, ∴AC=OC,∠AOC=60°, ∵CE∥AB, ∴AC=EB, ∴四边形ACEB是等腰梯形,OC=BE, ∴∠CAB=∠EBA=60°, ∴∠AOC=∠EBA=60°, ∴OC∥BE, ∴四边形COBE是平行四边形, ∵OC=OB, ∴以点C,O,B,E为顶点的四边形是菱形. ?/
28.【答案】∵∠B=30°,AC=2?/ ∴BA=4?/?∠A=60°, ∴CB=6, ∵AC=A′C, ∴∠AA′C是等边三角形, ∴∠ACA′=60°, ∴∠BCB′=60°, ∴弧长l=?/ 故答案为:2π.
29.【答案】解: / 共有6种情况,指针所指的两个数字之和为偶数的情况有3种, 因此王伟获胜的概率为
3
6
=
1
2
,李丽获胜的概率是
1
2
,所以这个方法公平.
一、单选题(共10题;共30分)
1.如图,点A,B,C均在⊙O上,若∠A=66°,则∠OCB的度数是( ??) /
A.?24°???????????????????????????????????????B.?28°???????????????????????????????????????C.?33°???????????????????????????????????????D.?48°
2.同时抛掷两枚均匀的硬币,落地后两枚硬币都是正面朝上的概率是(????? )
A.?1??????????????????????????????????????????/B.?
1
2
??????????????????????????????????????????/C.?
1
3
??????????????????????????????????????????/D.?
1
4
3.与如图所示的三视图对应的几何体是(?? ) /
A.?/???????????????????????????B.?/???????????????????????????C.?/???????????????????????????D.?/
4.下列图形中既是中心对称图形又是轴对称图形的是(???)
A.?/???????????????????????????B.?/???????????????????????????C.?/???????????????????????????D.?/
5.如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为(??? ) /
A.?
14
3
π﹣6?????????????????????????????/B.?
25
9
π?????????????????????????????/C.?
33
8
π﹣3?????????????????????????????/D.?
33
+π
6.如图,现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( ?? ? ) /
A.?4cm?????????????????????????????????????B.?3cm?????????????????????????????????????C.?2cm?????????????????????????????????????D.?1cm
7.如图1,分别以直角三角形三边为边向外作等边三角形,面积分别为S1、S2、S3;如图2,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S4、S5、S6 . 其中S1=16,S2=45,S5=11,S6=14,则S3+S4=( ) /
A.?86?????????????????????????????????????????B.?64?????????????????????????????????????????C.?54?????????????????????????????????????????D.?48
8.如图,AB是⊙O的直径,点C、D都在⊙O上,若∠C=20°,则∠ABD的度数等于( ) /?
A.?80°???????????????????????????????????????B.?70°???????????????????????????????????????C.?50°???????????????????????????????????????D.?40°
9.如图所示,在平面直角坐标系中,点A,B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A'的坐标为(??? ) /
A.?(2,2)???????????????????????????B.?(2,4)???????????????????????????C.?(4,2)???????????????????????????D.?(1,2)
10.点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=2,CD=3,则AE的长为( ) A.?2?????????????????????????????????????????/B.?2.5?????????????????????????????????????????/C.?3?????????????????????????????????????????/D.?3.5
二、填空题(共10题;共30分)
11.在一个不透明的盒子中装有n个规格相同的乒乓球,其中有2个黄色球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到黄色球的频率稳定于0.2,那么可以推算出n大约是________.
12.一个不透明的袋中装有2枚白色棋子和n枚黑色棋子,它们除颜色不同外,其余均相同.若小明从中随机摸出一枚棋子,多次实验后发现摸到黑色棋子的频率稳定在80%.则n很可能是________枚.
13.如图,在⊙O中,
????
∧
=
????
∧
,∠C=75°,则∠A=________?°. /
14.(2015?曲靖)一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗,每次随机摸出一颗珠子,放回摇匀后再摸,通过多次试验发现摸到白珠子的频率稳定在0.3左右,则盒子中黑珠子可能有________?颗.
15.如图(右上),在△ABC中,∠ABC=24°,以AB为直径的⊙O交BC于点D,交CA 的延长线于点E,若点E在BD的垂直平分线上,则∠C的度数为________.
/
16.? 3.12 日植树节,老师想从甲、乙、丙、丁4名同学中挑选2名同学代表班级去参加学校组织的植树活动,恰好选中甲和乙去参加的概率是________.
17.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于________?. /
18.如图,是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=1,则BB′的长为________?. /
19.在一个不透明的袋子中,有3个白球和1个红球,它们只有颜色上的区别,从袋子中随机摸出一个球记下颜色放回,再随机地摸出一个球,则两次都摸到白球的概率为________ .
20.如图,在菱形ABCD中,tanA=
3
,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=
3
4
CG2;其中正确结论的序号为________. /
三、解答题(共9题;共60分)
21.如图是由6个正方体组成的几何体,请分别画出从正面、左面、上面看到的这个几何体的形状图。 /
22.小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由. /
23.如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连接OE、AC,且∠P=∠E,∠POE=2∠CAB. /
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,PB=9,求⊙O的半径及tan∠P的值.
24.一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位上的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数.试问:按这种方法能组成哪些两位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
25.九年级学生小刚是一个喜欢看书的好学生,他在学习完第二十四章圆后,在家里突然看到爸爸的初中数学书上居然还有一个相交弦定理(圆内的两条相交弦,被交点分成的两条线段长的积相等),非常好奇,仔细阅读原来就是:PA?PB=PC?PD,小刚很想知道是如何证明的,可异证明部分污损看不清了,只看到辅助线的做法,分别连结AC、BD.聪明的你一定能帮他证出,请在图1中做出辅助线,并写出详细的证明过程. / 小刚又看到一道课后习题,如图2,AB是⊙O弦,P是AB上一点,AB=10cm,PA=4cm,OP=5cm,求⊙O的半径,愁坏了小刚,乐于助人的你肯定会帮助他,请写出详细的证明过程.
26.如图是一个正方体的展开图,标注了字母a的面是正方体的正面,如果正方体相对两个面上的整式的值相等,求整式(x+y)a的值.
/
27.如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E. (1)求∠D的度数; (2)求证:以点C,O,B,E为顶点的四边形是菱形. ?/
28.如图,三角板ABC中,∠ACB=90°,∠B=30°,AC=2 /,三角板绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边的起始位置上时即停止转动,求点B转过的路径长. /
29.学校奖励给王伟和李丽上海世博园门票共两张,其中一张为指定日门票,另一张为普通日门票.班长由王伟和李丽分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被三等分)确定指定日门票的归属,在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则王伟获得指定日门票;若指针所指的两个数字之和为奇数,则李丽获得指定日门票;若指针指向分隔线,则重新转动.你认为这个方法公平吗?请画树状图或列表,并说明理由. /
答案解析部分
一、单选题
1.【答案】A
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】A
8.【答案】B
9.【答案】B
10.【答案】B
二、填空题
11.【答案】10
12.【答案】8
13.【答案】30
14.【答案】14
15.【答案】33°
16.【答案】
1
6
17.【答案】40°
18.【答案】4
19.【答案】
9
16
20.【答案】(1)(3)(4)
三、解答题
21.【答案】解:正面看到的形状为: / 左面看到的形状为: / 正面看到的形状为: /
22.【答案】解:这个游戏规则对双方公平.理由如下: 画树状图为: / 共有9种等可能的结果数,其中摸出的两张卡片的正面数字之积小于10的结果数为4;摸出的两张卡片的正面数字之积超过10的结果数为4, 所以小明获胜的概率=
4
9
,小亮获胜的概率=
4
9
. 所以这个游戏规则对双方公平
23.【答案】(1)证明:连接OC, ∴∠COB=2∠CAB, 又∠POE=2∠CAB. ∴∠COD=∠EOD, 则弧BC=弧BE, 即CE⊥AB; / (2)证明:∵CE⊥AB,∠P=∠E, ∴∠P+∠PCD=∠E+∠PCD=90°, 又∠OCD=∠E, ∴∠OCD+∠PCD=∠PCO=90°, ∴PC是⊙O的切线; (3)解:设⊙O的半径为r,OD=x,则BD=2x,r=3x, ∵CD⊥OP,OC⊥PC, ∴Rt△OCD∽Rt△OPC, ∴OC2=OD?OP,即(3x)2=x?(3x+9), 解之得x=
3
2
, ∴⊙O的半径r=
9
2
, 在Rt△OCP中, PC=
??
??
2
???
??
2
=
(
9
2
+9)
2
+
(
9
2
)
2
=9
2
, tan∠P=
????
????
=
2
4
.
24.【答案】解:根据题意列表如下: / 十位上则十位上的数字和个位上的数字之和为9的两位数有45和54,所以其概率为:2÷9=
2
9
.
25.【答案】解:(1)圆的两条弦相交,这两条弦被交点分成的两条线段的积相等. 已知,如图1,⊙O的两弦AB、CD相交于E, 求证:AP?BP=CP?DP. 证明如下: 连结AC,BD,如图1, ∵∠C=∠B,∠A=∠D, ∴△APC∽△DPB, ∴AP:DP=CP:BP, ∴AP?BP=CP?DP; 所以两条弦相交,被交点分成的两条线段的积相等. (2)过P作直径CD,如图2, ∵AB=10,PA=4,OP=5, ∴PB=10﹣4=6,PC=OC﹣OP=R﹣5,PD=OD+OP=R+5, 由(1)中结论得,PA?PB=PC?PD, ∴4×6=(R﹣5)×(R+5), 解得R=7(R=﹣7舍去). 所以⊙O的半径R=7. /
26.【答案】81
解答:根据题意得:y=3,x=6,a=2,
故(x+y)a
=(x+y)2
=92
=81.
27.【答案】(1)解:连接AC, ∵CD是⊙O的切线, ∴∠ACD=∠ABC, ∵AB是直径, ∴∠ACB=90°, ∵CD=CB, ∴∠D=∠ABC, ∴∠D=∠ACD=∠ABC, ∵∠D+∠ACD+∠ABC+∠ACB=90°, ∴∠D=30°; (2)证明:连接OC、BE, ∵∠D=∠ACD=30°, ∴∠CAB=60°, ∵OA=OC, ∴△AOC是等边三角形, ∴AC=OC,∠AOC=60°, ∵CE∥AB, ∴AC=EB, ∴四边形ACEB是等腰梯形,OC=BE, ∴∠CAB=∠EBA=60°, ∴∠AOC=∠EBA=60°, ∴OC∥BE, ∴四边形COBE是平行四边形, ∵OC=OB, ∴以点C,O,B,E为顶点的四边形是菱形. ?/
28.【答案】∵∠B=30°,AC=2?/ ∴BA=4?/?∠A=60°, ∴CB=6, ∵AC=A′C, ∴∠AA′C是等边三角形, ∴∠ACA′=60°, ∴∠BCB′=60°, ∴弧长l=?/ 故答案为:2π.
29.【答案】解: / 共有6种情况,指针所指的两个数字之和为偶数的情况有3种, 因此王伟获胜的概率为
3
6
=
1
2
,李丽获胜的概率是
1
2
,所以这个方法公平.
同课章节目录
