苏科版九年级数学下册《第六章图形的相似》单元评估检测试卷(含答案)
文档属性
| 名称 | 苏科版九年级数学下册《第六章图形的相似》单元评估检测试卷(含答案) | 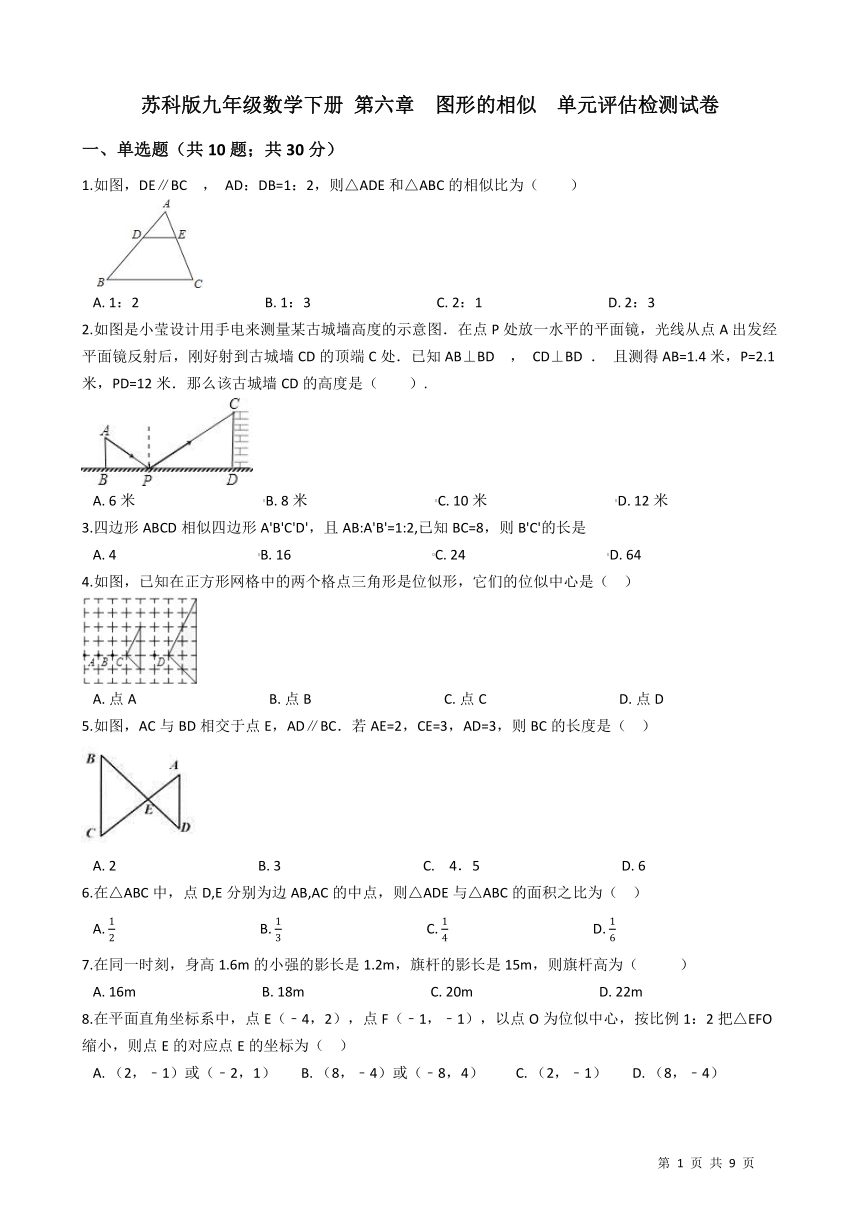 | |
| 格式 | zip | ||
| 文件大小 | 138.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-04 21:53:24 | ||
图片预览


文档简介
苏科版九年级数学下册 第六章 图形的相似 单元评估检测试卷
一、单选题(共10题;共30分)
1.如图,DE∥BC , AD:DB=1:2,则△ADE和△ABC的相似比为( )
/
A.?1:2????????????????????????????????????/B.?1:3????????????????????????????????????/C.?2:1????????????????????????????????????/D.?2:3
2.如图是小莹设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD , CD⊥BD . 且测得AB=1.4米,P=2.1米,PD=12米.那么该古城墙CD的高度是( ). /
A.?6米?????????????????????????????????????/B.?8米?????????????????????????????????????/C.?10米?????????????????????????????????????/D.?12米
3.四边形ABCD相似四边形A'B'C'D',且AB:A'B'=1:2,已知BC=8,则B'C'的长是
A.?4?????????????????????????????????????????/B.?16?????????????????????????????????????????/C.?24?????????????????????????????????????????/D.?64
4.如图,已知在正方形网格中的两个格点三角形是位似形,它们的位似中心是( ??) /
A.?点A??????????????????????????????????????/B.?点B??????????????????????????????????????/C.?点C??????????????????????????????????????/D.?点D
5.如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是(?? ) /
A.?2?????????????????????????????????????????/B.?3?????????????????????????????????????????/C.?? 4.5?????????????????????????????????????????/D.?6
6.在△ABC中,点D,E分别为边AB,AC的中点,则△ADE与△ABC的面积之比为(?? )
A.?
1
2
??????????????????????????????????????????/B.?
1
3
??????????????????????????????????????????/C.?
1
4
??????????????????????????????????????????/D.?
1
6
7.在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,则旗杆高为( ? ? ? )
A.?16m????????????????????????????????????/B.?18m????????????????????????????????????/C.?20m????????????????????????????????????/D.?22m
8.在平面直角坐标系中,点E(﹣4,2),点F(﹣1,﹣1),以点O为位似中心,按比例1:2把△EFO缩小,则点E的对应点E的坐标为(?? )
A.?(2,﹣1)或(﹣2,1)???????/B.?(8,﹣4)或(﹣8,4)?????????/C.?(2,﹣1)???????/D.?(8,﹣4)
9.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是(?? )
/
A.9.3m B.10.5m C.12.4m D.14m
10.(2016?深圳)如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: ①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ?AC, 其中正确的结论的个数是(? ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
二、填空题(共10题;共30分)
11.若两个相似多边形的面积比是16:25,则它们的周长比等于________.
12.在△ABC中,MN∥BC 分别交AB,AC于点M,N;若AM=1,MB=2,BC=3,则MN的长为________.
/
13.如图,直线AD∥BE∥CF,它们分别交直线l1、l2于点A,B,C和点D,E,F.若AB=2,BC=4,则
????
????
的值为________. /
14.如图,已知点C是线段AB的黄金分割点,若AB=2cm,则AC=________cm. /
15.有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形(如图).依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的________倍. /
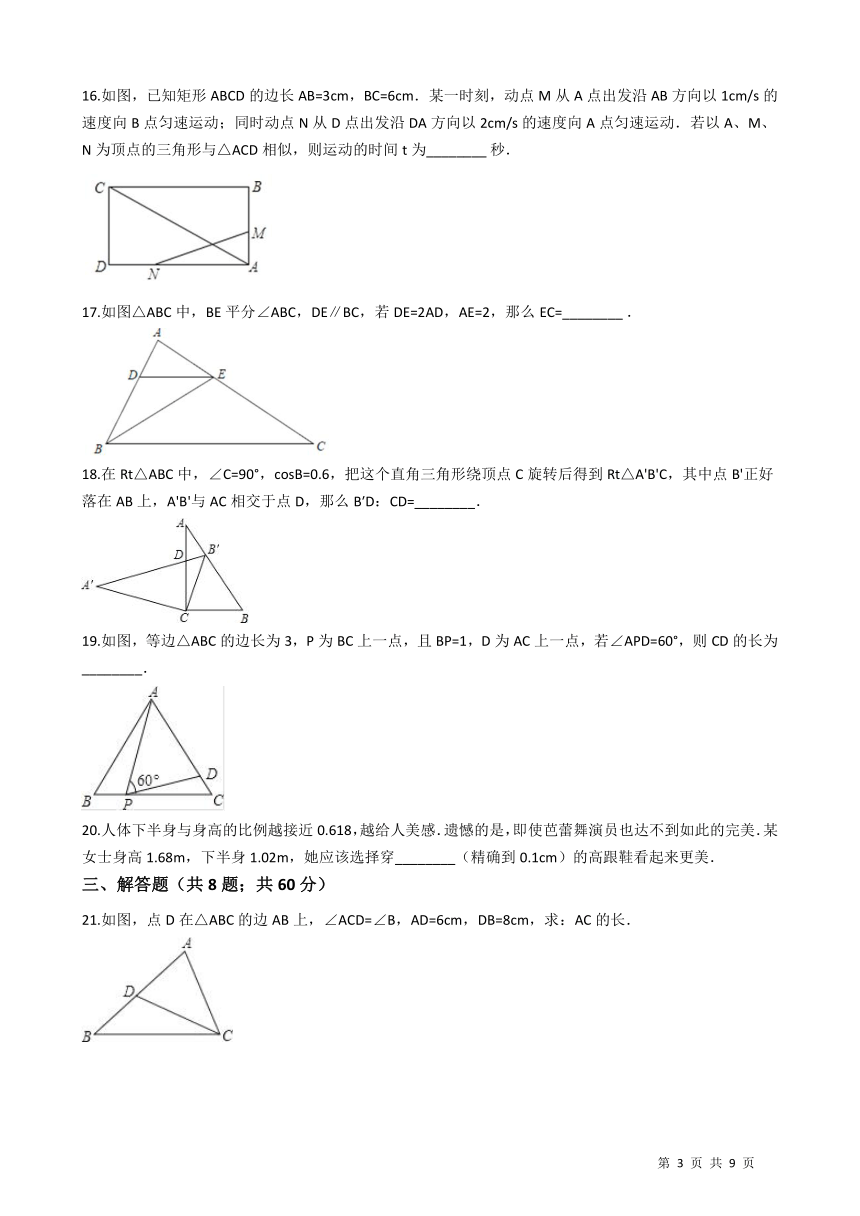
16.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间t为________?秒. ?/
17.如图△ABC中,BE平分∠ABC,DE∥BC,若DE=2AD,AE=2,那么EC=________?. ?/
18.在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=________. /
19.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为________. /
20.人体下半身与身高的比例越接近0.618,越给人美感.遗憾的是,即使芭蕾舞演员也达不到如此的完美.某女士身高1.68m,下半身1.02m,她应该选择穿________(精确到0.1cm)的高跟鞋看起来更美.
三、解答题(共8题;共60分)
21.如图,点D在△ABC的边AB上,∠ACD=∠B,AD=6cm,DB=8cm,求:AC的长. /
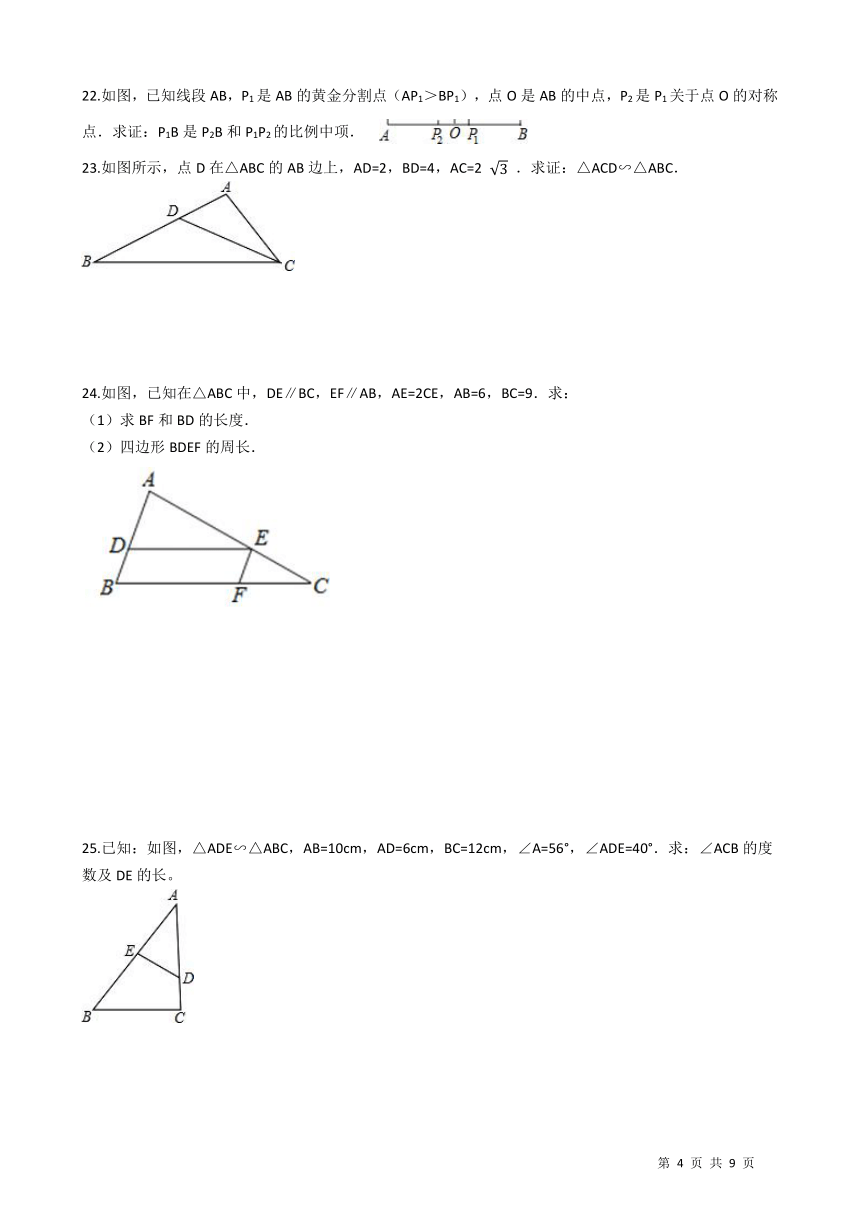
22.如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项. /
23.如图所示,点D在△ABC的AB边上,AD=2,BD=4,AC=2
3
.求证:△ACD∽△ABC. /
24.如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求: (1)求BF和BD的长度. (2)四边形BDEF的周长. ?/
25.已知:如图,△ADE∽△ABC,AB=10cm,AD=6cm,BC=12cm,∠A=56°,∠ADE=40°.求:∠ACB的度数及DE的长。 /
26.某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时点A,C,E三点共线. (1)请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影长FH(不写画法); (2)求小明到达点F时的影长FH的长. /
27.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.
(1)求证:△ACB∽△ADE;
(2)求AD的长度.
/
28.如图:已知△ABC∽△DEC,∠D=45°,∠ACB=60°,AC=3cm,BC=4cm,CE=6cm.求: (1)∠B的度数; (2)求AD的长. /
答案解析部分
一、单选题
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】B
10.【答案】D
二、填空题
11.【答案】4:5
12.【答案】1
13.【答案】
1
3
14.【答案】
5
﹣1
15.【答案】
1
4
16.【答案】2.4或1.5
17.【答案】4
18.【答案】0.35
19.【答案】/
20.【答案】4.8
三、解答题
21.【答案】解:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴
????
????
=
????
????
,即
6
????
=
????
8+6
,解得,AC=2
21
.
22.【答案】证明:设AB=2, ∵P1是AB的黄金分割点(AP1>BP1), ∴AP1= /×2= /﹣1, ∴P1B=2﹣( /﹣1)=3﹣ /, ∵点O是AB的中点, ∴OB=1, ∴OP1=1﹣(3﹣ /)= /﹣2, ∵P2是P1关于点O的对称点, ∴P1P2=2( /﹣2)=2 /﹣4, ∴P2B=2 /﹣4+3﹣ /= /﹣1, ∵P1B2=(3﹣ /)2=14﹣6 /,P2B?P1P2=( /﹣1)(2 /﹣4)=14﹣6 /, ∴P1B2=P2B?P1P2 , ∴P1B是P2B和P1P2的比例中项
23.【答案】证明:∵
????
????
=
2
2
3
=
3
3
,
????
????
=
2
3
6
=
3
3
∴
????
????
=
????
????
, 又∵∠A=∠A ∴△ACD∽△ABC
24.【答案】解:(1)∵AE=2CE, ∴
????
????
=
1
2
, ∵EF∥AB ∴
????
????
=
????
????
=
2
3
, ∵BC=9, ∴BF=6, ∵DE∥BC ∴
????
????
=
????
????
=
1
3
, ∵AB=6, ∴BD=2; (2)∵EF∥AB,DE∥BC ∴四边形BDEF是平行四边形, ∴BD=EF=2,DE=BF=6, ∴四边形BDEF的周长2(2+6)=16.
25.【答案】解:△AED中已知, ∵∠A=56°,∠ADE=40°, ∴∠AED=84°. ∵△ADE∽△ABC, ∴∠ACB=∠AED=84°,
DE
BC
=
AD
AB
. ∴
DE
12
=
6
10
. ∴DE=7.2(cm) 答:∠ACB的度数是84°,DE是7.2 cm。
26.【答案】解:(1)如图,点O和FH为所作; / (2)BM=BD=2×1.5=3m,GD=1.2m,DF=1.5×1.5×2=4.5m,设AB=CD=EF=a, 作OK⊥MN于K,如图, ∵AB∥OK, ∴△MAB∽△MOK, ∴
????
????
=
????
????
, 即
??
????
=
3
6+????
①, ∵CD∥OK, ∴△GCD∽△GOK, ∴
????
????
=
????
????
, 即
??
????
=
1.2
1.2+????
②, 由①②得
3
6+????
=
1.2
1.2+????
, 解得Dk=2, ∴
??
????
=
3
6+2
=
3
8
, FK=DF﹣DK=4.5﹣2=2.5, ∵EF∥OK, ∴△HEF∽△HOK, ∴
??
????
=
????
????
, 即
????
????+2.5
=
3
8
, ∴HF=1.5(m). 答:小明到达点F时的影长FH的长为1.5m.
27.【答案】证明:(1)∵DE⊥AB,∠C=90°,
∴∠EDA=∠C=90°,
∵∠A=∠A,
∴△ACB∽△ADE;
(2)解:∵△ACB∽△ADE,
∴
????
????
=
????
????
,
∴
5
10
=
????
8
,
∴AD=4.
28.【答案】解:(1)∵△ABC∽△DEC, ∴∠A=∠D=45°, 在△ACB中,∠B=180°﹣∠A﹣∠ACB=180°﹣45°﹣60°=75°; (2)∵△ABC∽△DEC, ∴
????
????
=
????
????
, 即DC=
????
????
×CE=
9
2
cm, ∴AD=AC+CD=
15
2
cm.
一、单选题(共10题;共30分)
1.如图,DE∥BC , AD:DB=1:2,则△ADE和△ABC的相似比为( )
/
A.?1:2????????????????????????????????????/B.?1:3????????????????????????????????????/C.?2:1????????????????????????????????????/D.?2:3
2.如图是小莹设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD , CD⊥BD . 且测得AB=1.4米,P=2.1米,PD=12米.那么该古城墙CD的高度是( ). /
A.?6米?????????????????????????????????????/B.?8米?????????????????????????????????????/C.?10米?????????????????????????????????????/D.?12米
3.四边形ABCD相似四边形A'B'C'D',且AB:A'B'=1:2,已知BC=8,则B'C'的长是
A.?4?????????????????????????????????????????/B.?16?????????????????????????????????????????/C.?24?????????????????????????????????????????/D.?64
4.如图,已知在正方形网格中的两个格点三角形是位似形,它们的位似中心是( ??) /
A.?点A??????????????????????????????????????/B.?点B??????????????????????????????????????/C.?点C??????????????????????????????????????/D.?点D
5.如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是(?? ) /
A.?2?????????????????????????????????????????/B.?3?????????????????????????????????????????/C.?? 4.5?????????????????????????????????????????/D.?6
6.在△ABC中,点D,E分别为边AB,AC的中点,则△ADE与△ABC的面积之比为(?? )
A.?
1
2
??????????????????????????????????????????/B.?
1
3
??????????????????????????????????????????/C.?
1
4
??????????????????????????????????????????/D.?
1
6
7.在同一时刻,身高1.6m的小强的影长是1.2m,旗杆的影长是15m,则旗杆高为( ? ? ? )
A.?16m????????????????????????????????????/B.?18m????????????????????????????????????/C.?20m????????????????????????????????????/D.?22m
8.在平面直角坐标系中,点E(﹣4,2),点F(﹣1,﹣1),以点O为位似中心,按比例1:2把△EFO缩小,则点E的对应点E的坐标为(?? )
A.?(2,﹣1)或(﹣2,1)???????/B.?(8,﹣4)或(﹣8,4)?????????/C.?(2,﹣1)???????/D.?(8,﹣4)
9.如图.利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,测得AB=1.6m.BC=12.4m.则建筑物CD的高是(?? )
/
A.9.3m B.10.5m C.12.4m D.14m
10.(2016?深圳)如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论: ①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ?AC, 其中正确的结论的个数是(? ) /
A.?1???????????????????????????????????????????/B.?2???????????????????????????????????????????/C.?3???????????????????????????????????????????/D.?4
二、填空题(共10题;共30分)
11.若两个相似多边形的面积比是16:25,则它们的周长比等于________.
12.在△ABC中,MN∥BC 分别交AB,AC于点M,N;若AM=1,MB=2,BC=3,则MN的长为________.
/
13.如图,直线AD∥BE∥CF,它们分别交直线l1、l2于点A,B,C和点D,E,F.若AB=2,BC=4,则
????
????
的值为________. /
14.如图,已知点C是线段AB的黄金分割点,若AB=2cm,则AC=________cm. /
15.有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形(如图).依照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的________倍. /
16.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间t为________?秒. ?/
17.如图△ABC中,BE平分∠ABC,DE∥BC,若DE=2AD,AE=2,那么EC=________?. ?/
18.在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=________. /
19.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为________. /
20.人体下半身与身高的比例越接近0.618,越给人美感.遗憾的是,即使芭蕾舞演员也达不到如此的完美.某女士身高1.68m,下半身1.02m,她应该选择穿________(精确到0.1cm)的高跟鞋看起来更美.
三、解答题(共8题;共60分)
21.如图,点D在△ABC的边AB上,∠ACD=∠B,AD=6cm,DB=8cm,求:AC的长. /
22.如图,已知线段AB,P1是AB的黄金分割点(AP1>BP1),点O是AB的中点,P2是P1关于点O的对称点.求证:P1B是P2B和P1P2的比例中项. /
23.如图所示,点D在△ABC的AB边上,AD=2,BD=4,AC=2
3
.求证:△ACD∽△ABC. /
24.如图,已知在△ABC中,DE∥BC,EF∥AB,AE=2CE,AB=6,BC=9.求: (1)求BF和BD的长度. (2)四边形BDEF的周长. ?/
25.已知:如图,△ADE∽△ABC,AB=10cm,AD=6cm,BC=12cm,∠A=56°,∠ADE=40°.求:∠ACB的度数及DE的长。 /
26.某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时点A,C,E三点共线. (1)请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影长FH(不写画法); (2)求小明到达点F时的影长FH的长. /
27.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.
(1)求证:△ACB∽△ADE;
(2)求AD的长度.
/
28.如图:已知△ABC∽△DEC,∠D=45°,∠ACB=60°,AC=3cm,BC=4cm,CE=6cm.求: (1)∠B的度数; (2)求AD的长. /
答案解析部分
一、单选题
1.【答案】B
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】B
10.【答案】D
二、填空题
11.【答案】4:5
12.【答案】1
13.【答案】
1
3
14.【答案】
5
﹣1
15.【答案】
1
4
16.【答案】2.4或1.5
17.【答案】4
18.【答案】0.35
19.【答案】/
20.【答案】4.8
三、解答题
21.【答案】解:∵∠ACD=∠B,∠A=∠A,∴△ADC∽△ACB,∴
????
????
=
????
????
,即
6
????
=
????
8+6
,解得,AC=2
21
.
22.【答案】证明:设AB=2, ∵P1是AB的黄金分割点(AP1>BP1), ∴AP1= /×2= /﹣1, ∴P1B=2﹣( /﹣1)=3﹣ /, ∵点O是AB的中点, ∴OB=1, ∴OP1=1﹣(3﹣ /)= /﹣2, ∵P2是P1关于点O的对称点, ∴P1P2=2( /﹣2)=2 /﹣4, ∴P2B=2 /﹣4+3﹣ /= /﹣1, ∵P1B2=(3﹣ /)2=14﹣6 /,P2B?P1P2=( /﹣1)(2 /﹣4)=14﹣6 /, ∴P1B2=P2B?P1P2 , ∴P1B是P2B和P1P2的比例中项
23.【答案】证明:∵
????
????
=
2
2
3
=
3
3
,
????
????
=
2
3
6
=
3
3
∴
????
????
=
????
????
, 又∵∠A=∠A ∴△ACD∽△ABC
24.【答案】解:(1)∵AE=2CE, ∴
????
????
=
1
2
, ∵EF∥AB ∴
????
????
=
????
????
=
2
3
, ∵BC=9, ∴BF=6, ∵DE∥BC ∴
????
????
=
????
????
=
1
3
, ∵AB=6, ∴BD=2; (2)∵EF∥AB,DE∥BC ∴四边形BDEF是平行四边形, ∴BD=EF=2,DE=BF=6, ∴四边形BDEF的周长2(2+6)=16.
25.【答案】解:△AED中已知, ∵∠A=56°,∠ADE=40°, ∴∠AED=84°. ∵△ADE∽△ABC, ∴∠ACB=∠AED=84°,
DE
BC
=
AD
AB
. ∴
DE
12
=
6
10
. ∴DE=7.2(cm) 答:∠ACB的度数是84°,DE是7.2 cm。
26.【答案】解:(1)如图,点O和FH为所作; / (2)BM=BD=2×1.5=3m,GD=1.2m,DF=1.5×1.5×2=4.5m,设AB=CD=EF=a, 作OK⊥MN于K,如图, ∵AB∥OK, ∴△MAB∽△MOK, ∴
????
????
=
????
????
, 即
??
????
=
3
6+????
①, ∵CD∥OK, ∴△GCD∽△GOK, ∴
????
????
=
????
????
, 即
??
????
=
1.2
1.2+????
②, 由①②得
3
6+????
=
1.2
1.2+????
, 解得Dk=2, ∴
??
????
=
3
6+2
=
3
8
, FK=DF﹣DK=4.5﹣2=2.5, ∵EF∥OK, ∴△HEF∽△HOK, ∴
??
????
=
????
????
, 即
????
????+2.5
=
3
8
, ∴HF=1.5(m). 答:小明到达点F时的影长FH的长为1.5m.
27.【答案】证明:(1)∵DE⊥AB,∠C=90°,
∴∠EDA=∠C=90°,
∵∠A=∠A,
∴△ACB∽△ADE;
(2)解:∵△ACB∽△ADE,
∴
????
????
=
????
????
,
∴
5
10
=
????
8
,
∴AD=4.
28.【答案】解:(1)∵△ABC∽△DEC, ∴∠A=∠D=45°, 在△ACB中,∠B=180°﹣∠A﹣∠ACB=180°﹣45°﹣60°=75°; (2)∵△ABC∽△DEC, ∴
????
????
=
????
????
, 即DC=
????
????
×CE=
9
2
cm, ∴AD=AC+CD=
15
2
cm.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
