陕西省澄城中学2018-2019学年高一上学期基础知识检测(三)数学试卷 (解析版)
文档属性
| 名称 | 陕西省澄城中学2018-2019学年高一上学期基础知识检测(三)数学试卷 (解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 279.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-06 00:00:00 | ||
图片预览




文档简介
澄城中学高一年级基础知识检测(3)
数 学 试 题
(本试卷满分150分,考试时间120分钟)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出下列几个命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中正确命题的个数是
A.0 B.1 C.2 D.3
2.下列结论正确的是
A.各个面都是三角形的几何体是三棱锥
B.以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥
C.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
D.圆锥的顶点与底面圆周上的任意一点的连线都是母线
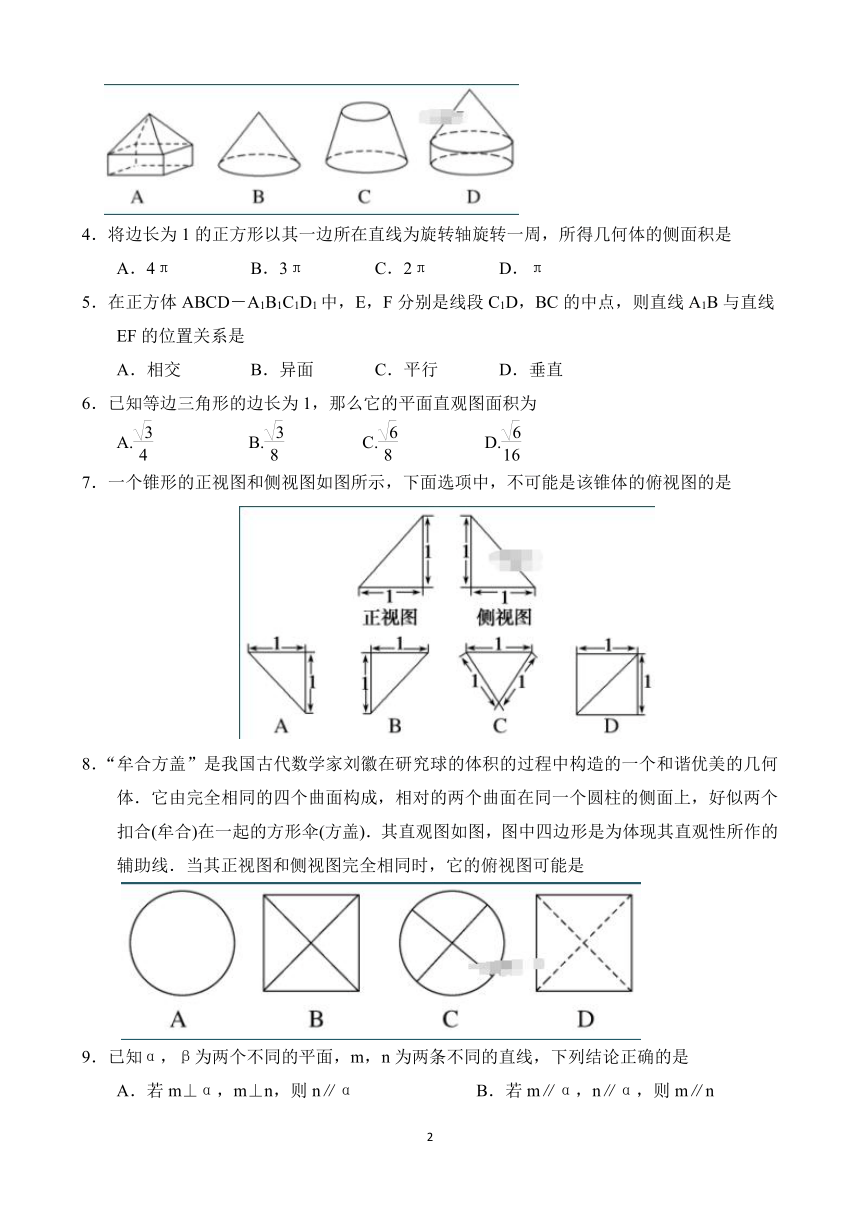
3.如图所示是一个物体的三视图,则此三视图所描述物体的直观
图是
4.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是
A.4π B.3π C.2π D.π
5.在正方体ABCD-A1B1C1D1中,E,F分别是线段C1D,BC的中点,则直线A1B与直线EF的位置关系是
A.相交 B.异面 C.平行 D.垂直
6.已知等边三角形的边长为1,那么它的平面直观图面积为
A. B. C. D.
7.一个锥形的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是
8.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是
9.已知α,β为两个不同的平面,m,n为两条不同的直线,下列结论正确的是
A.若m⊥α,m⊥n,则n∥α B.若m∥α,n∥α,则m∥n
C.若m β,且α⊥β,则m⊥α D.若m⊥β,且α∥β,则m⊥α
10.某几何体的三视图如图所示(单位:cm),则该几何体的体积是
A.8 cm3
B.12 cm3
C.cm3
D.cm3
11.如图所示,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,
点M为线段PB的中点.现有结论:
①BC⊥PC;
②OM∥平面APC;
③点B到平面PAC的距离等于线段BC的长,
其中正确的是
A.①② B.①②③ C.① D.②③
12.如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体ABCD,使平面ABD⊥平面BCD,若四面体ABCD的顶点在同一个球面上,则该球的体积为
A. B.3π C. D.2π
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.某四棱柱的三视图如图所示,则该四棱柱的体积为________.
已知PA,PB,PC两两垂直且PA=,PB=,PC=2,则过P,A,B,C四点的
球的体积为________.
已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则
该四棱锥的体积为________m3.
16.已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直; ②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积; ④直线AE与直线BF是异面直线.
以上结论正确的是________(写出所有正确结论的编号).
解答题(本大题共4小题,共70分.解答时应写出必要的文字说明、证明过程或演
算步骤)
17.(本小题满分15分)
如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:
(1)EG∥平面BB1D1D;
(2)平面BDF∥平面B1D1H.
18.(本小题满分15分)
如图所示,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4, AB=6,BC=3.
(1)证明:BC∥平面PDA;
(2)证明:BC⊥PD;
19.(本小题满分20分)
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
(1)证明:平面AEC⊥平面BED;
(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为,求该三棱锥的侧面积.
20.(本小题满分20分)
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若AD=2,PD=3,∠BAD=,求三棱锥P-ADM的体积.
澄城中学高一年级基础知识检测(3)
数学试题参考答案
选择题
1、解析:①不一定,只有这两点的连线平行于轴时才是母线;②正确;③错误,棱台的上、下底面是相似且对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.
答案:B
2、解析:A错误.如图1所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥.
B错误.如图2,若△ABC不是直角三角形或是直角三角形,但旋转轴不是直角边所在直线,所得的几何体都不是圆锥.
C错误.若六棱锥的所有棱长都相等,则底面多边形是正六边形.由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.D正确.
答案: D
3、解析:先观察俯视图,由俯视图可知选项B和D中的一个正确,由正视图和侧视图可知选项D正确,故选D.
答案:D
4、解析:由题意可知该几何体是底面半径r=1,母线l=1的圆柱,故S侧=2πrl=2π×1×1=2π.故选C.
答案:C
5、解析:因为A1B∥D1C,D1C∩EF=E,又E,F,A1,B四点都在平行四边形A1BCD1上,所以E,F,A1,B四点共面,所以EF与A1B相交,故选A.
答案:A
6、解析:底边长为1,高为××sin45°=,∴S=.
答案:D
7、解析:若俯视图为选项C,侧视图的宽应为俯视图中三角形的高,所以俯视图不可能是选项C.
答案:C
8、解析:根据直观图以及图中的辅助四边形分析可知,当正视图和侧视图完全相同时,俯视图为B,故选B.
答案:B
9、解析:A中可能n α;B中m,n还可能相交或异面;C中m,α还可能平行或斜交;一条直线垂直于两平行平面中的一个,也垂直于另一个,所以D正确.
答案:D
10、解析:由三视图可知,该几何体是由一个正方体和一个正四棱锥构成的组合体.下面是棱长为2 cm的正方体,体积V1=2×2×2=8(cm3);上面是底面边长为2 cm,高为2 cm的正四棱锥,体积V2=×2×2×2=(cm3),所以该几何体的体积V=V1+V2=(cm3).
答案:C
11、解析 对于①,∵PA⊥平面ABC,BC 平面ABC,∴PA⊥BC,
∵AB为圆O的直径,∴BC⊥AC,PA∩AC=A,∴BC⊥平面PAC,
又PC 平面PAC,∴BC⊥PC,①正确;
对于②,∵点M为线段PB的中点,∴OM∥PA,
∵PA 平面PAC,OM平面PAC,
∴OM∥平面PAC,②正确;
对于③,由①知BC⊥平面PAC,∴线段BC的长即是点B到平面PAC的距离,故①②③都正确.
答案 B
12、解析:
如图,取BD的中点为E,BC的中点为O,连接AE,OD,EO,AO.因为AB=AD,所以AE⊥BD.
由于平面ABD⊥平面BCD,
所以AE⊥平面BCD.
因为AB=AD=CD=1,BD=,
所以AE=,EO=.
所以AO=.
在Rt△BDC中,OB=OC=OD=BC=,所以四面体ABCD的外接球的球心为O,半径为.
所以该球的体积.
答案:A
填空题
13、解析:由题意知该四棱柱为直四棱柱,其高为1,其底面为上底长为1,下底长为2,高为1的等腰梯形,所以该四棱柱的体积为V=×1=.
答案:
14、解析:以PB,PA,PC为长方体的长、宽、高作长方体,则长方体的对角线长为,即球半径为,V球=πR=.
答案:π
15、解析:由三视图知,四棱锥的高为3,底面平行四边形的一边长为2,对应高为1,所以其体积V=Sh=×2×1×3=2.
答案:2
16、解析 由条件可得AB⊥平面PAD,
∴AB⊥PD,故①正确;
若平面PBC⊥平面ABCD,由PB⊥BC,
得PB⊥平面ABCD,从而PA∥PB,这显然不成立,故②错;
S△PCD=CD·PD,S△PAB=AB·PA,
由AB=CD,PD >PA知③正确;
由E、F分别是棱PC、PD的中点,
可得EF∥CD,又AB∥CD,
∴EF∥AB,故AE与BF共面,故④错.
答案 ①③
解答题
17、证明:(1)取B1D1的中点O,连接GO,OB,
易证四边形BEGO为平行四边形,故OB∥GE,
OB 平面BB1D1D,GE 平面BB1D1D,
由线面平行的判定定理即可证EG∥平面BB1D1D.
(2)由题意可知BD∥B1D1.
如图,连接HB、D1F,
易证四边形HBFD1是平行四边形,故HD1∥BF.
又B1D1∩HD1=D1, BD∩BF=B,
所以平面BDF∥平面B1D1H.
18、[解析] (1)因为四边形ABCD是长方形,所以BC∥AD,因为BC平面PDA,AD?平面PDA,所以BC∥平面PDA.
(2)因为四边形ABCD是长方形, 所以BC⊥CD,
因为平面PDC⊥平面ABCD,平面PDC ∩平面ABCD=CD,BC 平面ABCD,
所以BC⊥平面PDC,
因为PD 平面PDC, 所以BC⊥PD.
19、(1)证明 因为四边形ABCD为菱形,所以AC⊥BD.
因为BE⊥平面ABCD,AC 平面ABCD,所以AC⊥BE.又BE∩BD=B,所以AC⊥平面BED.又AC 平面AEC,所以平面AEC⊥平面BED.
(2)解.设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=x,GB=GD=.
因为AE⊥EC,所以在Rt△AEC中,可得EG=x.
由BE⊥平面ABCD,知△EBG为直角三角形,由勾股定理可得BE=x.
由已知得,三棱锥E-ACD的体积VE-ACD=×AC×GD×BE=x3=,故x=2.
从而可得AE=EC=ED=.
所以△EAC的面积为3,△EAD的面积与△ECD的面积均为.
故三棱锥E-ACD的侧面积为3+2.
20、解 (1)如图,过M作MN∥CD交PD于点N,连接AN.
∵PM=2MC,∴MN=CD.
又AB=CD,且AB∥CD,
∴ABMN,∴四边形ABMN为平行四边形, ∴BM∥AN.
又BM 平面PAD,AN 平面PAD, ∴BM∥平面PAD.
(2)如图,过B作AD的垂线,垂足为E.
∵PD⊥平面ABCD,BE 平面ABCD, ∴PD⊥BE.
又AD平面PAD,PD平面PAD,AD∩PD=D.
∴BE⊥平面PAD.
由(1)知,BM∥平面PAD,
∴点M到平面PAD的距离等于点B到平面PAD的距离,即BE.
连接BD,在△ABD中,AB=AD=2,∠BAD=,∴BE=,
则三棱锥P-ADM的体积VP-ADM=VM-PAD=×S△PAD×BE=×3×=.
数 学 试 题
(本试卷满分150分,考试时间120分钟)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出下列几个命题:
①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
②底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱;
③棱台的上、下底面可以不相似,但侧棱长一定相等.
其中正确命题的个数是
A.0 B.1 C.2 D.3
2.下列结论正确的是
A.各个面都是三角形的几何体是三棱锥
B.以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥
C.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥
D.圆锥的顶点与底面圆周上的任意一点的连线都是母线
3.如图所示是一个物体的三视图,则此三视图所描述物体的直观
图是
4.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是
A.4π B.3π C.2π D.π
5.在正方体ABCD-A1B1C1D1中,E,F分别是线段C1D,BC的中点,则直线A1B与直线EF的位置关系是
A.相交 B.异面 C.平行 D.垂直
6.已知等边三角形的边长为1,那么它的平面直观图面积为
A. B. C. D.
7.一个锥形的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是
8.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如图,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是
9.已知α,β为两个不同的平面,m,n为两条不同的直线,下列结论正确的是
A.若m⊥α,m⊥n,则n∥α B.若m∥α,n∥α,则m∥n
C.若m β,且α⊥β,则m⊥α D.若m⊥β,且α∥β,则m⊥α
10.某几何体的三视图如图所示(单位:cm),则该几何体的体积是
A.8 cm3
B.12 cm3
C.cm3
D.cm3
11.如图所示,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,
点M为线段PB的中点.现有结论:
①BC⊥PC;
②OM∥平面APC;
③点B到平面PAC的距离等于线段BC的长,
其中正确的是
A.①② B.①②③ C.① D.②③
12.如图所示,平面四边形ABCD中,AB=AD=CD=1,BD=,BD⊥CD,将其沿对角线BD折成四面体ABCD,使平面ABD⊥平面BCD,若四面体ABCD的顶点在同一个球面上,则该球的体积为
A. B.3π C. D.2π
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.某四棱柱的三视图如图所示,则该四棱柱的体积为________.
已知PA,PB,PC两两垂直且PA=,PB=,PC=2,则过P,A,B,C四点的
球的体积为________.
已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则
该四棱锥的体积为________m3.
16.已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直; ②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积; ④直线AE与直线BF是异面直线.
以上结论正确的是________(写出所有正确结论的编号).
解答题(本大题共4小题,共70分.解答时应写出必要的文字说明、证明过程或演
算步骤)
17.(本小题满分15分)
如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:
(1)EG∥平面BB1D1D;
(2)平面BDF∥平面B1D1H.
18.(本小题满分15分)
如图所示,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4, AB=6,BC=3.
(1)证明:BC∥平面PDA;
(2)证明:BC⊥PD;
19.(本小题满分20分)
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
(1)证明:平面AEC⊥平面BED;
(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为,求该三棱锥的侧面积.
20.(本小题满分20分)
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若AD=2,PD=3,∠BAD=,求三棱锥P-ADM的体积.
澄城中学高一年级基础知识检测(3)
数学试题参考答案
选择题
1、解析:①不一定,只有这两点的连线平行于轴时才是母线;②正确;③错误,棱台的上、下底面是相似且对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.
答案:B
2、解析:A错误.如图1所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥.
B错误.如图2,若△ABC不是直角三角形或是直角三角形,但旋转轴不是直角边所在直线,所得的几何体都不是圆锥.
C错误.若六棱锥的所有棱长都相等,则底面多边形是正六边形.由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.D正确.
答案: D
3、解析:先观察俯视图,由俯视图可知选项B和D中的一个正确,由正视图和侧视图可知选项D正确,故选D.
答案:D
4、解析:由题意可知该几何体是底面半径r=1,母线l=1的圆柱,故S侧=2πrl=2π×1×1=2π.故选C.
答案:C
5、解析:因为A1B∥D1C,D1C∩EF=E,又E,F,A1,B四点都在平行四边形A1BCD1上,所以E,F,A1,B四点共面,所以EF与A1B相交,故选A.
答案:A
6、解析:底边长为1,高为××sin45°=,∴S=.
答案:D
7、解析:若俯视图为选项C,侧视图的宽应为俯视图中三角形的高,所以俯视图不可能是选项C.
答案:C
8、解析:根据直观图以及图中的辅助四边形分析可知,当正视图和侧视图完全相同时,俯视图为B,故选B.
答案:B
9、解析:A中可能n α;B中m,n还可能相交或异面;C中m,α还可能平行或斜交;一条直线垂直于两平行平面中的一个,也垂直于另一个,所以D正确.
答案:D
10、解析:由三视图可知,该几何体是由一个正方体和一个正四棱锥构成的组合体.下面是棱长为2 cm的正方体,体积V1=2×2×2=8(cm3);上面是底面边长为2 cm,高为2 cm的正四棱锥,体积V2=×2×2×2=(cm3),所以该几何体的体积V=V1+V2=(cm3).
答案:C
11、解析 对于①,∵PA⊥平面ABC,BC 平面ABC,∴PA⊥BC,
∵AB为圆O的直径,∴BC⊥AC,PA∩AC=A,∴BC⊥平面PAC,
又PC 平面PAC,∴BC⊥PC,①正确;
对于②,∵点M为线段PB的中点,∴OM∥PA,
∵PA 平面PAC,OM平面PAC,
∴OM∥平面PAC,②正确;
对于③,由①知BC⊥平面PAC,∴线段BC的长即是点B到平面PAC的距离,故①②③都正确.
答案 B
12、解析:
如图,取BD的中点为E,BC的中点为O,连接AE,OD,EO,AO.因为AB=AD,所以AE⊥BD.
由于平面ABD⊥平面BCD,
所以AE⊥平面BCD.
因为AB=AD=CD=1,BD=,
所以AE=,EO=.
所以AO=.
在Rt△BDC中,OB=OC=OD=BC=,所以四面体ABCD的外接球的球心为O,半径为.
所以该球的体积.
答案:A
填空题
13、解析:由题意知该四棱柱为直四棱柱,其高为1,其底面为上底长为1,下底长为2,高为1的等腰梯形,所以该四棱柱的体积为V=×1=.
答案:
14、解析:以PB,PA,PC为长方体的长、宽、高作长方体,则长方体的对角线长为,即球半径为,V球=πR=.
答案:π
15、解析:由三视图知,四棱锥的高为3,底面平行四边形的一边长为2,对应高为1,所以其体积V=Sh=×2×1×3=2.
答案:2
16、解析 由条件可得AB⊥平面PAD,
∴AB⊥PD,故①正确;
若平面PBC⊥平面ABCD,由PB⊥BC,
得PB⊥平面ABCD,从而PA∥PB,这显然不成立,故②错;
S△PCD=CD·PD,S△PAB=AB·PA,
由AB=CD,PD >PA知③正确;
由E、F分别是棱PC、PD的中点,
可得EF∥CD,又AB∥CD,
∴EF∥AB,故AE与BF共面,故④错.
答案 ①③
解答题
17、证明:(1)取B1D1的中点O,连接GO,OB,
易证四边形BEGO为平行四边形,故OB∥GE,
OB 平面BB1D1D,GE 平面BB1D1D,
由线面平行的判定定理即可证EG∥平面BB1D1D.
(2)由题意可知BD∥B1D1.
如图,连接HB、D1F,
易证四边形HBFD1是平行四边形,故HD1∥BF.
又B1D1∩HD1=D1, BD∩BF=B,
所以平面BDF∥平面B1D1H.
18、[解析] (1)因为四边形ABCD是长方形,所以BC∥AD,因为BC平面PDA,AD?平面PDA,所以BC∥平面PDA.
(2)因为四边形ABCD是长方形, 所以BC⊥CD,
因为平面PDC⊥平面ABCD,平面PDC ∩平面ABCD=CD,BC 平面ABCD,
所以BC⊥平面PDC,
因为PD 平面PDC, 所以BC⊥PD.
19、(1)证明 因为四边形ABCD为菱形,所以AC⊥BD.
因为BE⊥平面ABCD,AC 平面ABCD,所以AC⊥BE.又BE∩BD=B,所以AC⊥平面BED.又AC 平面AEC,所以平面AEC⊥平面BED.
(2)解.设AB=x,在菱形ABCD中,由∠ABC=120°,可得AG=GC=x,GB=GD=.
因为AE⊥EC,所以在Rt△AEC中,可得EG=x.
由BE⊥平面ABCD,知△EBG为直角三角形,由勾股定理可得BE=x.
由已知得,三棱锥E-ACD的体积VE-ACD=×AC×GD×BE=x3=,故x=2.
从而可得AE=EC=ED=.
所以△EAC的面积为3,△EAD的面积与△ECD的面积均为.
故三棱锥E-ACD的侧面积为3+2.
20、解 (1)如图,过M作MN∥CD交PD于点N,连接AN.
∵PM=2MC,∴MN=CD.
又AB=CD,且AB∥CD,
∴ABMN,∴四边形ABMN为平行四边形, ∴BM∥AN.
又BM 平面PAD,AN 平面PAD, ∴BM∥平面PAD.
(2)如图,过B作AD的垂线,垂足为E.
∵PD⊥平面ABCD,BE 平面ABCD, ∴PD⊥BE.
又AD平面PAD,PD平面PAD,AD∩PD=D.
∴BE⊥平面PAD.
由(1)知,BM∥平面PAD,
∴点M到平面PAD的距离等于点B到平面PAD的距离,即BE.
连接BD,在△ABD中,AB=AD=2,∠BAD=,∴BE=,
则三棱锥P-ADM的体积VP-ADM=VM-PAD=×S△PAD×BE=×3×=.
同课章节目录
