华师大版九年级数学上册课件:24.2 直角三角形性质(共23张PPT)
文档属性
| 名称 | 华师大版九年级数学上册课件:24.2 直角三角形性质(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-07 00:00:00 | ||
图片预览




文档简介
课件23张PPT。第24章解直角三角形24.2 直角三角形的性质
1、掌握“直角三角形斜边上的中线等于斜边的一半”定理以及应用.
2、巩固以及利用添辅助线证明有关几何问题的方法.
3、掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.教学目标1、什么叫做直角三角形?2、直角三角形是一类特殊的三角形,除了具备三角形的性质外,还具备哪些性质?问题3:在Rt△ABC中,∠C=900,两直角边
长分别为a,b斜边长为c,
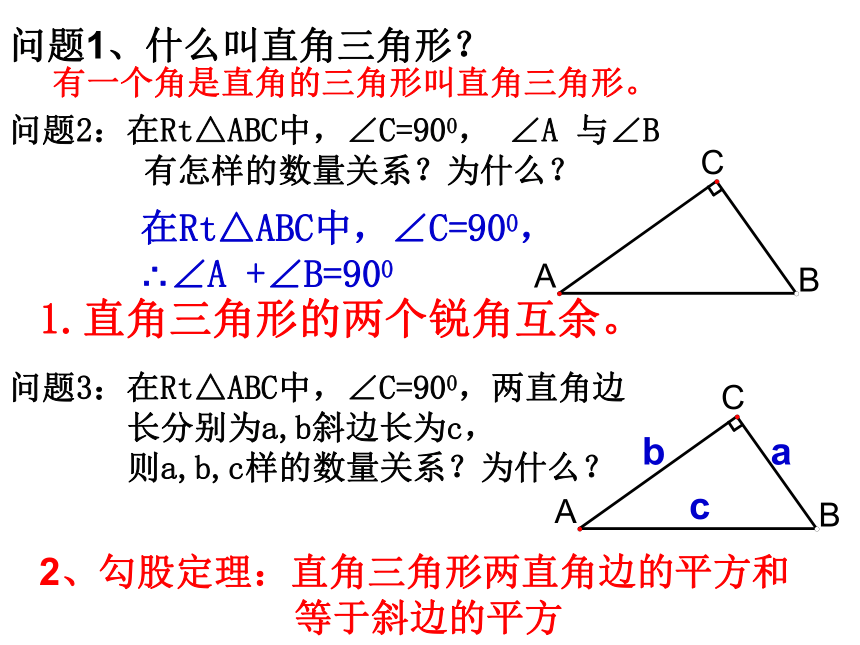
则a,b,c样的数量关系?为什么?在Rt△ABC中,∠C=900,
∴∠A +∠B=9001.直角三角形的两个锐角互余。问题2:在Rt△ABC中,∠C=900, ∠A 与∠B 有怎样的数量关系?为什么?2、勾股定理:直角三角形两直角边的平方和
等于斜边的平方 问题1、什么叫直角三角形?有一个角是直角的三角形叫直角三角形。与∠B互余的角有? ?? ????,
与∠A互余的角有??? ???,
与∠B相等的角有?????? ??? ,
与∠A相等的角有???? ????. (1)在直角三角形中,有一个锐角为520,那么另一个锐角度数为? ?????;
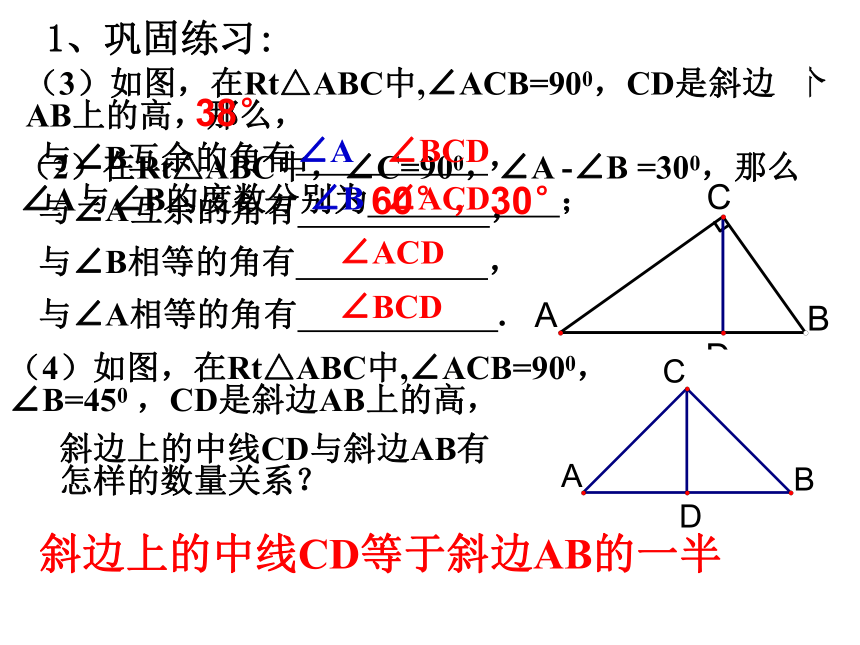
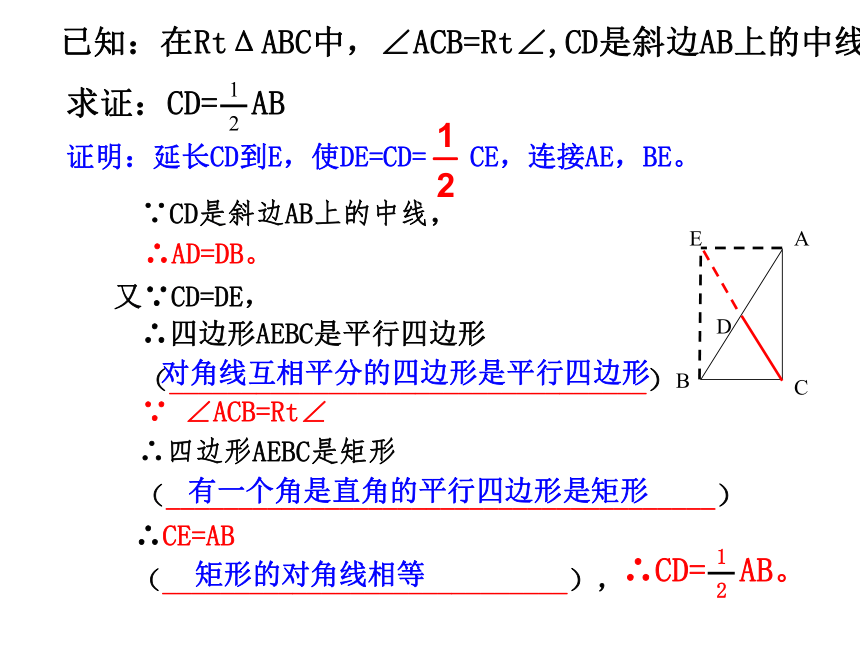
(2)在Rt△ABC中,∠C=900,∠A -∠B =300,那么∠A与∠B的度数分别为? ????? ;1、巩固练习:(3)如图,在Rt△ABC中,∠ACB=900,CD是斜边AB上的高,那么,∠A∠BCD∠B∠ACD∠ACD∠BCD(4)如图,在Rt△ABC中,∠ACB=900, ∠B=450 ,CD是斜边AB上的高,斜边上的中线CD与斜边AB有怎样的数量关系?斜边上的中线CD等于斜边AB的一半38°60°,30°命题:直角三角形斜边上的中线等于斜边的一半 证明:延长CD到点E,使DE=DC,连接AE.已知:在RtΔABC中,∠ACB=Rt∠,CD是斜边AB上的中线ACBDE证明:延长CD到E,使DE=CD= CE,连接AE,BE。 ∵CD是斜边AB上的中线,∴AD=DB。又∵CD=DE,∴四边形AEBC是平行四边形
(_________________________________)∴CE=AB(____________________________),∵ ∠ACB=Rt∠∴四边形AEBC是矩形
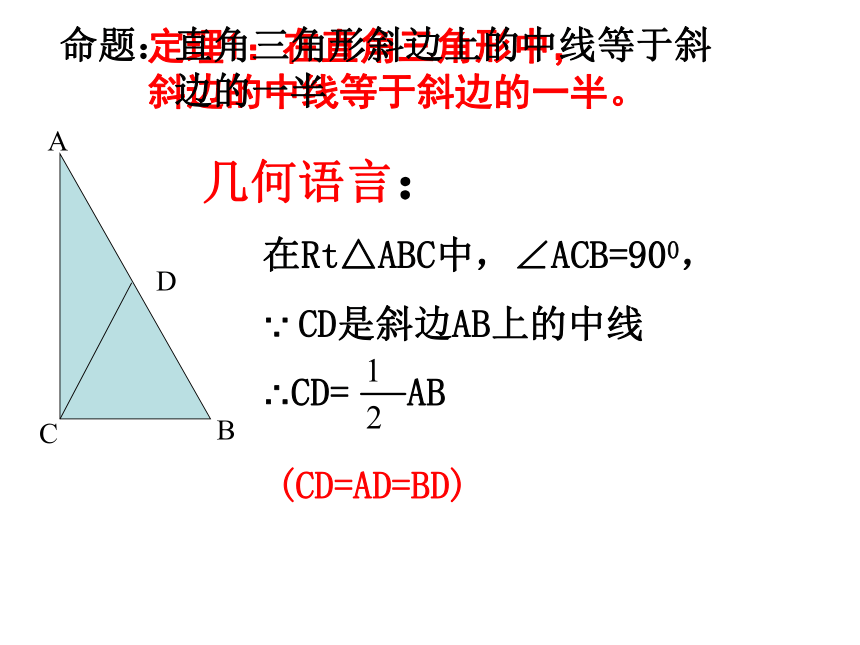
(______________________________________)对角线互相平分的四边形是平行四边形 有一个角是直角的平行四边形是矩形矩形的对角线相等 定理1:在直角三角形中,斜边的中线等于斜边的一半。命题:直角三角形斜边上的中线等于斜
边的一半 在Rt△ABC中,∠ACB=900,
∵ CD是斜边AB上的中线
∴CD= AB(CD=AD=BD)几何语言:证明:作斜边AB上的中线CD,则
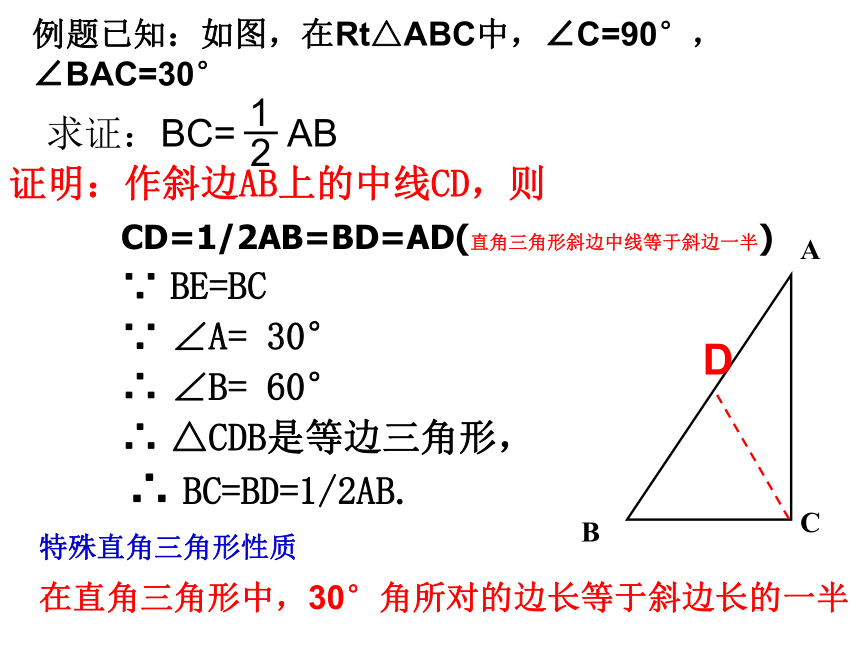
CD=1/2AB=BD=AD(直角三角形斜边中线等于斜边一半)
∵ BE=BC
∵ ∠A= 30°
∴ ∠B= 60°
∴ △CDB是等边三角形,
∴ BC=BD=1/2AB.D例题已知:如图,在Rt△ABC中,∠C=90°,∠BAC=30°在直角三角形中,30°角所对的边长等于斜边长的一半特殊直角三角形性质已知:如图,在Rt△ABC中,∠C=90°, ∠BAC=30°证明:延长BC至D,使CD=BC,连结AD.BCD∴ △ABC≌△ADC(SAS)在△ABC与△ADC中∴AB=AD又∵ △ABC 是等边三角形证法二:含30 °直角三角形性质:在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半。几何语言
∵在Rt△ABC中,∠C=90°,∠A= 30° ∴ BC= AB
)30°ABC300141.在△ABC中,∠C=900, ∠B=600,BC=7,
则∠A = ----------,AB=----------2.在△ABC中,∠A: ∠B: ∠C=1:2:3,
若AB=10,则BC=----------53、如图Rt△ABC中,CD是斜边AB
上的高,若∠A=300,BD=1cm,
那么∠BCD=_____, BC=_____.3002cm4cm2cm4、如图所示,已知△ABC中,∠ACB=900,
CD⊥AB于D, ∠A=300,且AB=8cm,
则BC= ---------- , ∠BCD=----------,
BD= ---------- ,AD= ---------- , 5、如图△ABC是等边三角形,
AB=5cm,AD⊥BC,DE⊥AB,DF⊥AC,
垂足分别为D、E、F点,
则∠ADF =______, BD=______,
BE=_______.1.25cm2.5cm60°3006cm1、如图,在Rt△ABC中∠C=900 ,∠B=2 ∠A,
AB=6cm,则BC=________.2、如图, Rt△ABC中, ∠A= 30°,
AB+BC=12cm,则AB= _______.3cm8cm3、如图, Rt△ABC中, ∠A= 30°,BD平分∠ABC,
且BD=16cm,则AD= .24cmD1、在△ABC中, ∠ACB=90 °,CE是AB边上的中线,那么与CE相等的线段有______,与∠A相等的角有_____,若∠A=35°,那么∠ECB= ______.2、在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________. 巩固新知,深化提高: EA,BE∠ACE55°4例3、如图,在△ABC中,AD⊥BC,E、F
分别是AB、AC的中点,且DE=DF.求证:AB=AC证明:∵ AD⊥BC
∴ ∠ADB= ∠ADC=90°在Rt△ADB中,E为斜边AB中点
∴ AB = 2DE同理:AC = 2DF又∵ DE = DF∴ AB = AC变式1、如图,在△ABC中,AD⊥BC,E、F分别是AB、AC的中点,且AB=AC.
求证: DE=DF证明:∵ AD⊥BC
∴ ∠ADB= ∠ADC=90°在Rt△ADB中,E为斜边AB中点
∴ DE= 1/2AB同理:DF =1/2AC又∵ AB = AC∴ DE = DF如图1,在Rt △ ABC与Rt △ ACE中,∠ABC=∠AEC=90 °,点M是AC边上的中点,联结BM、EM、BE,点P是BE的中点. 求证:E试一试 : 直角三角形的性质ABCMP证明:(已知)∵ ∠ ABC= ∠ AEC=90° M是AC边上的中点(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)∴ BM= EM又∵ P是BE边上的中点∴ MP ⊥ BE (等腰三角形三线合一)(图1)MP ⊥ BE . 直角三角形的性质C证明:∵ ∠ ABC= ∠ AEC=90 ° M是AC边上的中点∴ BM= EM又∵ P是BE边上的中点∴ MP ⊥BE (已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)如图2,在Rt△ABC与Rt△ACE中,∠ ABC=∠ AEC=90°,
点M是AC边上的中点,联结BM、EM、BE,点P是BE的中点. 求证:MP ⊥ BE .(图2)M小结:斜边重合的两个直角三角形,其斜边的中线相等 直角三角形的性质EDACMP如图3,在△ACD中,AE、CB分别是边CD、AD上的高,M、 P分别是AC、BE的中点.
求证:MP ⊥ BE .试一试 :证明:∵ ∠AEC= ∠ABC=90 ° M是AC边上的中点∴ ME= MB又∵ P是BE边上的中点∴ MP ⊥ BE (图3)(已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)B联结ME、MB如图,已知BC=20m, ∠B=∠C=30°, E、G分别为AB,AC的中点,P为BC的中点,且EF⊥BC, GH⊥BC,垂足分别为F,H,求EF、PG的长;练一练课堂小结:证明一条线段是另一条线段的1/2或2倍,
(1)常用的定理:(2)添辅助线的方法: “三角形的中位线定理”和“直角三角形的斜边上的中线等于斜边的一半” 延长短的一倍,再证它与长的线段相等;或在长的上截取中点,再证中点取得的一半等于短的,1、直角三角形的两个锐角互余2、直角三角形中两直角边的平方和等于斜边的平方3、直角三角形斜边上的中线等于斜边的一半祝学习进步课本P104练习1,2 ,3。
课本P104-105习题1,2,3。
跟踪两本练习册作业书痴者文必工,艺痴者技必良。
——蒲松龄
1、掌握“直角三角形斜边上的中线等于斜边的一半”定理以及应用.
2、巩固以及利用添辅助线证明有关几何问题的方法.
3、掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.教学目标1、什么叫做直角三角形?2、直角三角形是一类特殊的三角形,除了具备三角形的性质外,还具备哪些性质?问题3:在Rt△ABC中,∠C=900,两直角边
长分别为a,b斜边长为c,
则a,b,c样的数量关系?为什么?在Rt△ABC中,∠C=900,
∴∠A +∠B=9001.直角三角形的两个锐角互余。问题2:在Rt△ABC中,∠C=900, ∠A 与∠B 有怎样的数量关系?为什么?2、勾股定理:直角三角形两直角边的平方和
等于斜边的平方 问题1、什么叫直角三角形?有一个角是直角的三角形叫直角三角形。与∠B互余的角有? ?? ????,
与∠A互余的角有??? ???,
与∠B相等的角有?????? ??? ,
与∠A相等的角有???? ????. (1)在直角三角形中,有一个锐角为520,那么另一个锐角度数为? ?????;
(2)在Rt△ABC中,∠C=900,∠A -∠B =300,那么∠A与∠B的度数分别为? ????? ;1、巩固练习:(3)如图,在Rt△ABC中,∠ACB=900,CD是斜边AB上的高,那么,∠A∠BCD∠B∠ACD∠ACD∠BCD(4)如图,在Rt△ABC中,∠ACB=900, ∠B=450 ,CD是斜边AB上的高,斜边上的中线CD与斜边AB有怎样的数量关系?斜边上的中线CD等于斜边AB的一半38°60°,30°命题:直角三角形斜边上的中线等于斜边的一半 证明:延长CD到点E,使DE=DC,连接AE.已知:在RtΔABC中,∠ACB=Rt∠,CD是斜边AB上的中线ACBDE证明:延长CD到E,使DE=CD= CE,连接AE,BE。 ∵CD是斜边AB上的中线,∴AD=DB。又∵CD=DE,∴四边形AEBC是平行四边形
(_________________________________)∴CE=AB(____________________________),∵ ∠ACB=Rt∠∴四边形AEBC是矩形
(______________________________________)对角线互相平分的四边形是平行四边形 有一个角是直角的平行四边形是矩形矩形的对角线相等 定理1:在直角三角形中,斜边的中线等于斜边的一半。命题:直角三角形斜边上的中线等于斜
边的一半 在Rt△ABC中,∠ACB=900,
∵ CD是斜边AB上的中线
∴CD= AB(CD=AD=BD)几何语言:证明:作斜边AB上的中线CD,则
CD=1/2AB=BD=AD(直角三角形斜边中线等于斜边一半)
∵ BE=BC
∵ ∠A= 30°
∴ ∠B= 60°
∴ △CDB是等边三角形,
∴ BC=BD=1/2AB.D例题已知:如图,在Rt△ABC中,∠C=90°,∠BAC=30°在直角三角形中,30°角所对的边长等于斜边长的一半特殊直角三角形性质已知:如图,在Rt△ABC中,∠C=90°, ∠BAC=30°证明:延长BC至D,使CD=BC,连结AD.BCD∴ △ABC≌△ADC(SAS)在△ABC与△ADC中∴AB=AD又∵ △ABC 是等边三角形证法二:含30 °直角三角形性质:在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半。几何语言
∵在Rt△ABC中,∠C=90°,∠A= 30° ∴ BC= AB
)30°ABC300141.在△ABC中,∠C=900, ∠B=600,BC=7,
则∠A = ----------,AB=----------2.在△ABC中,∠A: ∠B: ∠C=1:2:3,
若AB=10,则BC=----------53、如图Rt△ABC中,CD是斜边AB
上的高,若∠A=300,BD=1cm,
那么∠BCD=_____, BC=_____.3002cm4cm2cm4、如图所示,已知△ABC中,∠ACB=900,
CD⊥AB于D, ∠A=300,且AB=8cm,
则BC= ---------- , ∠BCD=----------,
BD= ---------- ,AD= ---------- , 5、如图△ABC是等边三角形,
AB=5cm,AD⊥BC,DE⊥AB,DF⊥AC,
垂足分别为D、E、F点,
则∠ADF =______, BD=______,
BE=_______.1.25cm2.5cm60°3006cm1、如图,在Rt△ABC中∠C=900 ,∠B=2 ∠A,
AB=6cm,则BC=________.2、如图, Rt△ABC中, ∠A= 30°,
AB+BC=12cm,则AB= _______.3cm8cm3、如图, Rt△ABC中, ∠A= 30°,BD平分∠ABC,
且BD=16cm,则AD= .24cmD1、在△ABC中, ∠ACB=90 °,CE是AB边上的中线,那么与CE相等的线段有______,与∠A相等的角有_____,若∠A=35°,那么∠ECB= ______.2、在直角三角形中,斜边及其中线之和为6,那么该三角形的斜边长为________. 巩固新知,深化提高: EA,BE∠ACE55°4例3、如图,在△ABC中,AD⊥BC,E、F
分别是AB、AC的中点,且DE=DF.求证:AB=AC证明:∵ AD⊥BC
∴ ∠ADB= ∠ADC=90°在Rt△ADB中,E为斜边AB中点
∴ AB = 2DE同理:AC = 2DF又∵ DE = DF∴ AB = AC变式1、如图,在△ABC中,AD⊥BC,E、F分别是AB、AC的中点,且AB=AC.
求证: DE=DF证明:∵ AD⊥BC
∴ ∠ADB= ∠ADC=90°在Rt△ADB中,E为斜边AB中点
∴ DE= 1/2AB同理:DF =1/2AC又∵ AB = AC∴ DE = DF如图1,在Rt △ ABC与Rt △ ACE中,∠ABC=∠AEC=90 °,点M是AC边上的中点,联结BM、EM、BE,点P是BE的中点. 求证:E试一试 : 直角三角形的性质ABCMP证明:(已知)∵ ∠ ABC= ∠ AEC=90° M是AC边上的中点(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)∴ BM= EM又∵ P是BE边上的中点∴ MP ⊥ BE (等腰三角形三线合一)(图1)MP ⊥ BE . 直角三角形的性质C证明:∵ ∠ ABC= ∠ AEC=90 ° M是AC边上的中点∴ BM= EM又∵ P是BE边上的中点∴ MP ⊥BE (已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)如图2,在Rt△ABC与Rt△ACE中,∠ ABC=∠ AEC=90°,
点M是AC边上的中点,联结BM、EM、BE,点P是BE的中点. 求证:MP ⊥ BE .(图2)M小结:斜边重合的两个直角三角形,其斜边的中线相等 直角三角形的性质EDACMP如图3,在△ACD中,AE、CB分别是边CD、AD上的高,M、 P分别是AC、BE的中点.
求证:MP ⊥ BE .试一试 :证明:∵ ∠AEC= ∠ABC=90 ° M是AC边上的中点∴ ME= MB又∵ P是BE边上的中点∴ MP ⊥ BE (图3)(已知)(已知)(等量代换)(直角三角形斜边上的中线等于斜边的一半)(等腰三角形三线合一)B联结ME、MB如图,已知BC=20m, ∠B=∠C=30°, E、G分别为AB,AC的中点,P为BC的中点,且EF⊥BC, GH⊥BC,垂足分别为F,H,求EF、PG的长;练一练课堂小结:证明一条线段是另一条线段的1/2或2倍,
(1)常用的定理:(2)添辅助线的方法: “三角形的中位线定理”和“直角三角形的斜边上的中线等于斜边的一半” 延长短的一倍,再证它与长的线段相等;或在长的上截取中点,再证中点取得的一半等于短的,1、直角三角形的两个锐角互余2、直角三角形中两直角边的平方和等于斜边的平方3、直角三角形斜边上的中线等于斜边的一半祝学习进步课本P104练习1,2 ,3。
课本P104-105习题1,2,3。
跟踪两本练习册作业书痴者文必工,艺痴者技必良。
——蒲松龄
