湘教版九年级上《第四章锐角三角函数》单元评估试卷(有答案)
文档属性
| 名称 | 湘教版九年级上《第四章锐角三角函数》单元评估试卷(有答案) | 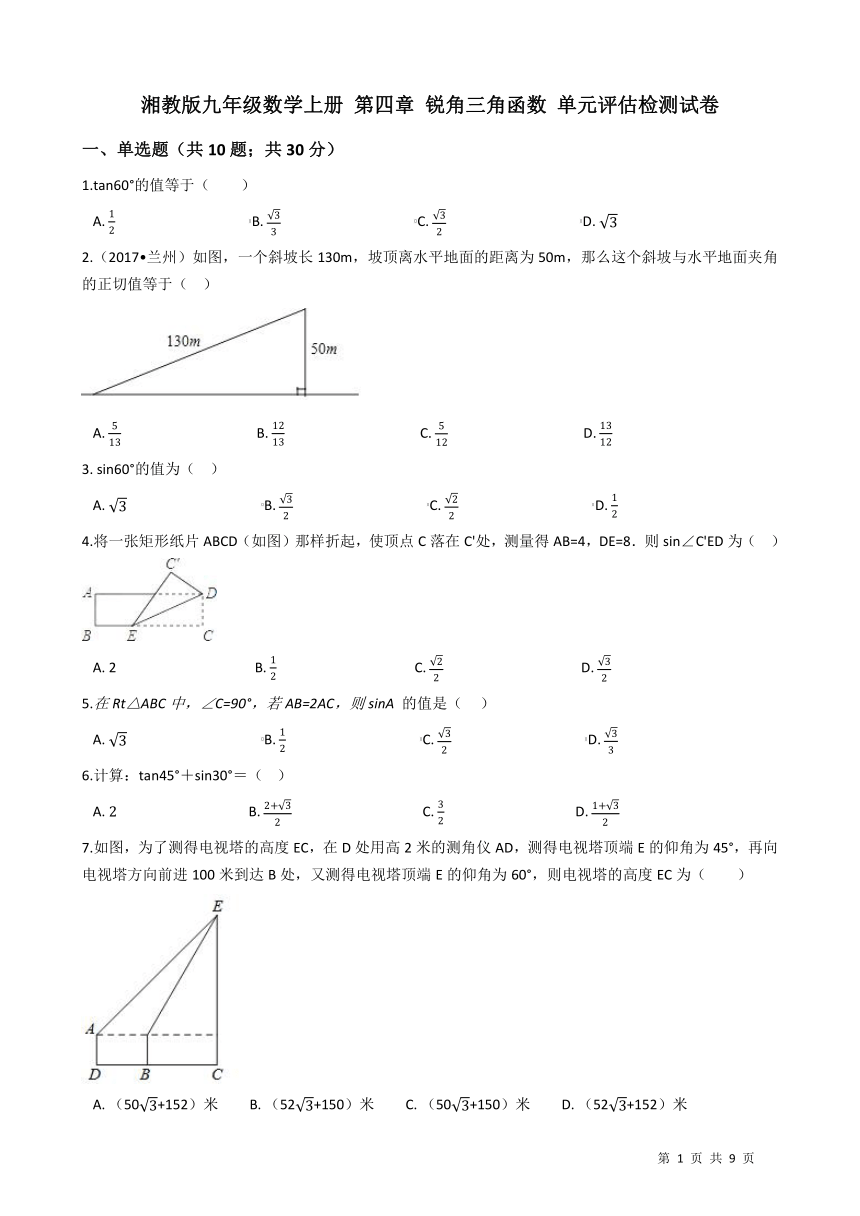 | |
| 格式 | zip | ||
| 文件大小 | 115.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-01-05 18:40:25 | ||
图片预览



文档简介
湘教版九年级数学上册 第四章 锐角三角函数 单元评估检测试卷
一、单选题(共10题;共30分)
1.tan60°的值等于( )
A.?
1
2
???????????????????????????????????????/B.?
3
3
???????????????????????????????????????/C.?
3
2
???????????????????????????????????????/D.?
3
2.(2017?兰州)如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡与水平地面夹角的正切值等于(?? ) /
A.?
5
13
???????????????????????????????????????/B.?
12
13
???????????????????????????????????????/C.?
5
12
???????????????????????????????????????/D.?
13
12
3. sin60°的值为(?? )
A.?
3
???????????????????????????????????????/B.?
3
2
???????????????????????????????????????/C.?
2
2
???????????????????????????????????????/D.?
1
2
4.将一张矩形纸片ABCD(如图)那样折起,使顶点C落在C'处,测量得AB=4,DE=8.则sin∠C'ED为( ??) /
A.?2????????????????????????????????????????/B.?
1
2
????????????????????????????????????????/C.?
2
2
????????????????????????????????????????/D.?
3
2
?
5.在Rt△ABC中,∠C=90°,若AB=2AC,则sinA 的值是(?????)
A.?
3
???????????????????????????????????????/B.?
1
2
???????????????????????????????????????/C.?
3
2
???????????????????????????????????????/D.?
3
3
6.计算:tan45°+sin30°=(????)
A.?2??????????????????????????????????????/B.?
2+
3
2
??????????????????????????????????????/C.?
3
2
??????????????????????????????????????/D.?
1+
3
2
7.如图,为了测得电视塔的高度EC,在D处用高2米的测角仪AD,测得电视塔顶端E的仰角为45°,再向电视塔方向前进100米到达B处,又测得电视塔顶端E的仰角为60°,则电视塔的高度EC为( ) /
A.?(50
3
+152)米?????????B.?(52
3
+150)米?????????C.?(50
3
+150)米?????????D.?(52
3
+152)米
8.在Rt△ABC中,∠C=90°,AC=3,BC=4,那么cosB的值是(????)
A.?
4
5
??????????????????????????????????????????B.?
3
5
??????????????????????????????????????????C.?
3
4
??????????????????????????????????????????D.?
4
3
9.已知Rt△ABC中,∠C=90°,tanA=
4
3
,BC=8,则AC等于(??? )
A.?6?????????????????????????????????????????/B.?
32
3
?????????????????????????????????????????/C.?10?????????????????????????????????????????/D.?12
10.如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为(? ) /
A.?2????????????????????????????????????????B.?
1
2
????????????????????????????????????????C.?
5
5
????????????????????????????????????????D.?
2
5
5
二、填空题(共10题;共30分)
11.在Rt△ABC中,∠C=90°,AB=3,BC=2,则cosA的值是________.
12.如果沿斜坡AB向上前进20米,升高10米,那么斜坡AB的坡度为________.
13.如果在平面直角坐标系xoy中,点P的坐标为(3,4),射线OP与X轴的正半轴所夹的角为α,那么α的余弦值等于________.
14.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=
1
5
, 则AD的长为________.
15.如图,在?ABCD中,AD=7,AB=2
3
,∠B=60°.E是边BC上任意一点,沿AE剪开,将△ABE沿BC方向平移到△DCF的位置,得到四边形AEFD,则四边形AEFD周长的最小值为________. /
16.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼高________?m(结果保留根号). /
17.△ABC之中, ∠BAC=90°,点D在直线AB上,连接DC,若tanB=
1
2
,AB=3,AD=2,则△DBC的面积为________. 18.如图,某人在塔顶的P处观测地平面上点C处,经测量∠ P=35°,则他从P处观察C处的俯角是________?度. /
19.在Rt△ABC中,∠C=90°,有两边长分别为3和4,则sinA的值为________?.
20.一次函数y=
4
3
x+b(b<0)与y=
4
3
x﹣1图象之间的距离等于3,则b的值为________.
三、解答题(共8题;共60分)
21.如图,从热气球C处测得地面A,B两点的俯角分别为 30° , 45° ,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离. /
22.如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积 ? /
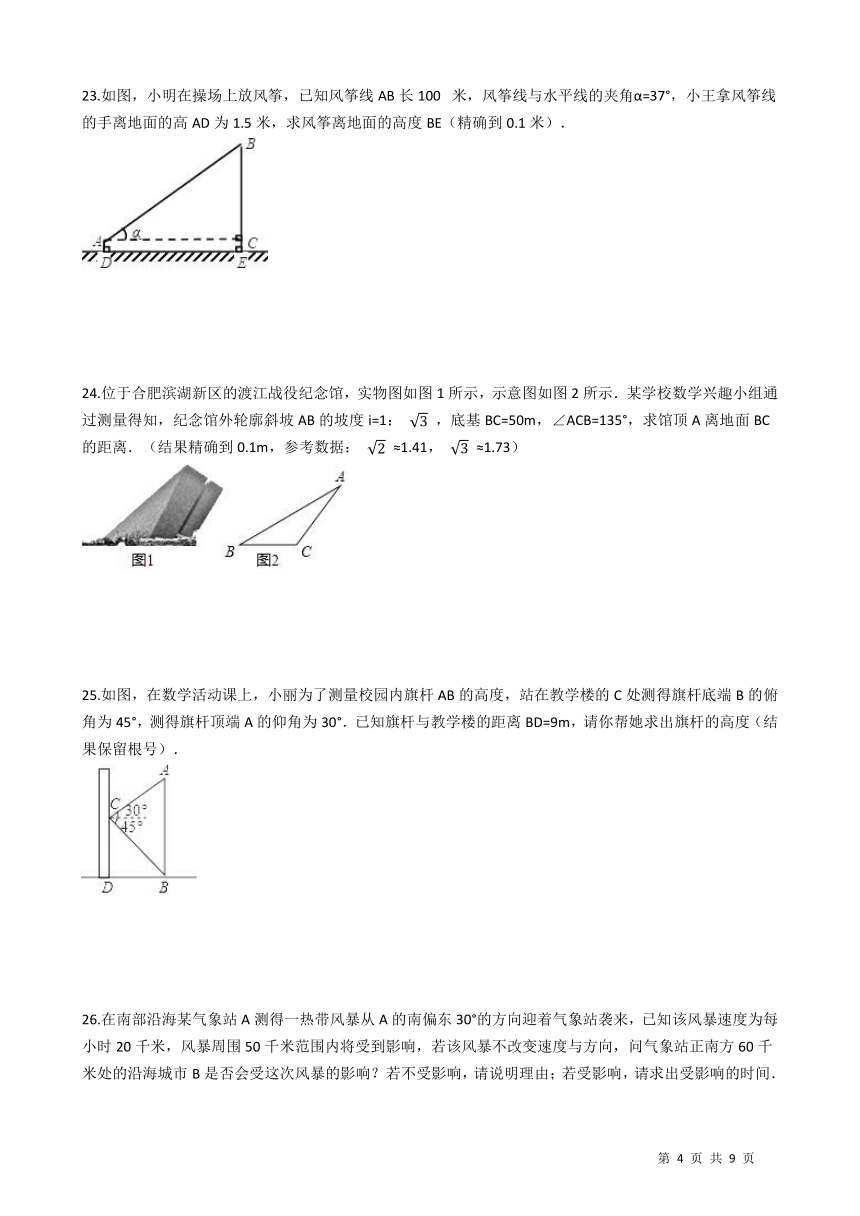
23.如图,小明在操场上放风筝,已知风筝线AB长100? 米,风筝线与水平线的夹角α=37°,小王拿风筝线的手离地面的高AD为1.5米,求风筝离地面的高度BE(精确到0.1米). /
24.位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:
3
,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:
2
≈1.41,
3
≈1.73) /
25.如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号). /
26.在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
27.如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C,楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度(结果精确到0.1m).(参考数据:
2
≈1.41,
3
≈1.73) /
28.如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= /:3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: /≈1.414, /≈1.732) /?
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】A
9.【答案】A
10.【答案】B
二、填空题
11.【答案】
5
3
12.【答案】1:
3
13.【答案】/
14.【答案】2
15.【答案】20
16.【答案】160
3
17.【答案】
15
4
或
3
4
18.【答案】55
19.【答案】
4
5
或
3
5
或
3
4
或
7
4
20.【答案】﹣6
三、解答题
21.【答案】解: 过点C作 ????⊥???? 于点D / 由题意得 ∠??=∠??????=30° , ∠??=∠??????=45° ∵在Rt△ACD中, sin??=
????
????
, cos??=
????
????
∴CD=AC sin?? = 400sin30° =400×
1
2
=200(m)? AD= AC cos?? = 400cos30° =400×
3
2
=200
3
(m) ∵在Rt△BCD中, tanB=
????
????
∴BD=
????
tan??
=
200
tan45°
=200 (m) ∴AB=AD+BD= (200
3
+200) m 答:地面上A,B两点间的距离为 (200
3
+200) m .
22.【答案】解:∵斜坡AB的坡度i=1:2.5,∴
????
????
=
1
2.5
, ∵斜坡CD的坡度i=1:2,∴
????
????
=
1
2
, ∵BE=20米,∴AE=50米,DF=40米, ∵EF=BC,BC=5米, ∴EF=5米, ∴AD=AE+EF+DF=50+5+40=95米 ∴S梯形ABCD=
1
2
?(AD+BC)×BE=
1
2
×100×20=1000(平方米)
23.【答案】解:∵AB=100米,α=37°, ∴BC=AB?sinα=100sin37°, ∵AD=CE=1.5米, ∴BE=BC+CE=100×sin37°+1.5≈100×0.60+1.5=61.5(米), 答:风筝离地面的高度BE为:61.5米
24.【答案】解:如解图,过点A作AD⊥BC交BC的延长线于点D. ∵∠ACB=135°, ∴△ADC为等腰直角三角形, 设AD=x,则CD=x,BD=50+x, ∵斜坡AB的坡度i=1:, ∴x:(50+x)=1:, 整理得(﹣1)x=50, 解得x=25(+1)≈68.3. 答:馆顶A离地面BC的距离约为68.3 m. /
25.【答案】解:如图, / 在Rt△ACF中, ∵tan∠ACF=
????
????
, ∴tan30°=
????
9
, ∴
????
9
=
3
3
, ∴AF=3
3
m, 在Rt△BCF中, ∵∠BCF=45°, ∴BF=CF=9m, ∴AB=AF+BF=3
3
+9(m).
26.【答案】解:根据题意画出图形, / 根据题意可知AB=60千米,∠BAF=30° 过B作BD⊥AF于点D,作BE=BF=50千米,分别交AF于点E、F ∵ BD⊥AF,AB=60千米,∠BAF=30° ∴ 风暴离B城市的最近距离为BD=AB×sin30°=30千米, ∵ BD<50千米 ∴ 沿海城市B会受到这次风暴的影响 ∵ BE=BF=50千米 ∴ 沿海城市B受影响时风暴所走的路程为线段EF ∵ BE=BF=50千米,BD=30千米,BD⊥AF ∴ DF=DE=
50
2
?
30
2
=40 ∴ EF=2DF=80千米 ∵ 风暴速度为每小时20千米 ∴ 受影响时间=
80
20
=4小时 ∴沿海城市B会受到这次风暴的影响,受影响的时间为4小时。
27.【答案】解:过点D作DE⊥AB于点E,得矩形DEBC, 设塔高AB=xm,则AE=(x﹣10)m, 在Rt△ADE中,∠ADE=30°, 则DE=
3
(x﹣10)米, 在Rt△ABC中,∠ACB=45°, 则BC=AB=x, 由题意得,
3
(x﹣10)=x, 解得:x=15+5
3
≈23.7.即AB≈23.7米. 答:塔的高度约为23.7米. /
28.【答案】解:需要拆除,理由为: ∵CB⊥AB , ∠CAB=45°, ∴△ABC为等腰直角三角形, ∴AB=BC=10米, 在Rt△BCD中,新坡面DC的坡度为i= /:3,即∠CDB=30°, ∴DC=2BC=20米,BD= /米, ∴AD=BD-AB=(10 /-10)米≈7.32米, ∵3+7.32=10.32>10, ∴需要拆除 .
一、单选题(共10题;共30分)
1.tan60°的值等于( )
A.?
1
2
???????????????????????????????????????/B.?
3
3
???????????????????????????????????????/C.?
3
2
???????????????????????????????????????/D.?
3
2.(2017?兰州)如图,一个斜坡长130m,坡顶离水平地面的距离为50m,那么这个斜坡与水平地面夹角的正切值等于(?? ) /
A.?
5
13
???????????????????????????????????????/B.?
12
13
???????????????????????????????????????/C.?
5
12
???????????????????????????????????????/D.?
13
12
3. sin60°的值为(?? )
A.?
3
???????????????????????????????????????/B.?
3
2
???????????????????????????????????????/C.?
2
2
???????????????????????????????????????/D.?
1
2
4.将一张矩形纸片ABCD(如图)那样折起,使顶点C落在C'处,测量得AB=4,DE=8.则sin∠C'ED为( ??) /
A.?2????????????????????????????????????????/B.?
1
2
????????????????????????????????????????/C.?
2
2
????????????????????????????????????????/D.?
3
2
?
5.在Rt△ABC中,∠C=90°,若AB=2AC,则sinA 的值是(?????)
A.?
3
???????????????????????????????????????/B.?
1
2
???????????????????????????????????????/C.?
3
2
???????????????????????????????????????/D.?
3
3
6.计算:tan45°+sin30°=(????)
A.?2??????????????????????????????????????/B.?
2+
3
2
??????????????????????????????????????/C.?
3
2
??????????????????????????????????????/D.?
1+
3
2
7.如图,为了测得电视塔的高度EC,在D处用高2米的测角仪AD,测得电视塔顶端E的仰角为45°,再向电视塔方向前进100米到达B处,又测得电视塔顶端E的仰角为60°,则电视塔的高度EC为( ) /
A.?(50
3
+152)米?????????B.?(52
3
+150)米?????????C.?(50
3
+150)米?????????D.?(52
3
+152)米
8.在Rt△ABC中,∠C=90°,AC=3,BC=4,那么cosB的值是(????)
A.?
4
5
??????????????????????????????????????????B.?
3
5
??????????????????????????????????????????C.?
3
4
??????????????????????????????????????????D.?
4
3
9.已知Rt△ABC中,∠C=90°,tanA=
4
3
,BC=8,则AC等于(??? )
A.?6?????????????????????????????????????????/B.?
32
3
?????????????????????????????????????????/C.?10?????????????????????????????????????????/D.?12
10.如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为(? ) /
A.?2????????????????????????????????????????B.?
1
2
????????????????????????????????????????C.?
5
5
????????????????????????????????????????D.?
2
5
5
二、填空题(共10题;共30分)
11.在Rt△ABC中,∠C=90°,AB=3,BC=2,则cosA的值是________.
12.如果沿斜坡AB向上前进20米,升高10米,那么斜坡AB的坡度为________.
13.如果在平面直角坐标系xoy中,点P的坐标为(3,4),射线OP与X轴的正半轴所夹的角为α,那么α的余弦值等于________.
14.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=
1
5
, 则AD的长为________.
15.如图,在?ABCD中,AD=7,AB=2
3
,∠B=60°.E是边BC上任意一点,沿AE剪开,将△ABE沿BC方向平移到△DCF的位置,得到四边形AEFD,则四边形AEFD周长的最小值为________. /
16.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼高________?m(结果保留根号). /
17.△ABC之中, ∠BAC=90°,点D在直线AB上,连接DC,若tanB=
1
2
,AB=3,AD=2,则△DBC的面积为________. 18.如图,某人在塔顶的P处观测地平面上点C处,经测量∠ P=35°,则他从P处观察C处的俯角是________?度. /
19.在Rt△ABC中,∠C=90°,有两边长分别为3和4,则sinA的值为________?.
20.一次函数y=
4
3
x+b(b<0)与y=
4
3
x﹣1图象之间的距离等于3,则b的值为________.
三、解答题(共8题;共60分)
21.如图,从热气球C处测得地面A,B两点的俯角分别为 30° , 45° ,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离. /
22.如图,水库大坝的横截面是梯形,坝顶宽5米,坝高20米,斜坡AB的坡比为1:2.5,斜坡CD的坡比为1:2,求大坝的截面面积 ? /
23.如图,小明在操场上放风筝,已知风筝线AB长100? 米,风筝线与水平线的夹角α=37°,小王拿风筝线的手离地面的高AD为1.5米,求风筝离地面的高度BE(精确到0.1米). /
24.位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1:
3
,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:
2
≈1.41,
3
≈1.73) /
25.如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号). /
26.在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
27.如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C,楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度(结果精确到0.1m).(参考数据:
2
≈1.41,
3
≈1.73) /
28.如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= /:3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: /≈1.414, /≈1.732) /?
答案解析部分
一、单选题
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】A
9.【答案】A
10.【答案】B
二、填空题
11.【答案】
5
3
12.【答案】1:
3
13.【答案】/
14.【答案】2
15.【答案】20
16.【答案】160
3
17.【答案】
15
4
或
3
4
18.【答案】55
19.【答案】
4
5
或
3
5
或
3
4
或
7
4
20.【答案】﹣6
三、解答题
21.【答案】解: 过点C作 ????⊥???? 于点D / 由题意得 ∠??=∠??????=30° , ∠??=∠??????=45° ∵在Rt△ACD中, sin??=
????
????
, cos??=
????
????
∴CD=AC sin?? = 400sin30° =400×
1
2
=200(m)? AD= AC cos?? = 400cos30° =400×
3
2
=200
3
(m) ∵在Rt△BCD中, tanB=
????
????
∴BD=
????
tan??
=
200
tan45°
=200 (m) ∴AB=AD+BD= (200
3
+200) m 答:地面上A,B两点间的距离为 (200
3
+200) m .
22.【答案】解:∵斜坡AB的坡度i=1:2.5,∴
????
????
=
1
2.5
, ∵斜坡CD的坡度i=1:2,∴
????
????
=
1
2
, ∵BE=20米,∴AE=50米,DF=40米, ∵EF=BC,BC=5米, ∴EF=5米, ∴AD=AE+EF+DF=50+5+40=95米 ∴S梯形ABCD=
1
2
?(AD+BC)×BE=
1
2
×100×20=1000(平方米)
23.【答案】解:∵AB=100米,α=37°, ∴BC=AB?sinα=100sin37°, ∵AD=CE=1.5米, ∴BE=BC+CE=100×sin37°+1.5≈100×0.60+1.5=61.5(米), 答:风筝离地面的高度BE为:61.5米
24.【答案】解:如解图,过点A作AD⊥BC交BC的延长线于点D. ∵∠ACB=135°, ∴△ADC为等腰直角三角形, 设AD=x,则CD=x,BD=50+x, ∵斜坡AB的坡度i=1:, ∴x:(50+x)=1:, 整理得(﹣1)x=50, 解得x=25(+1)≈68.3. 答:馆顶A离地面BC的距离约为68.3 m. /
25.【答案】解:如图, / 在Rt△ACF中, ∵tan∠ACF=
????
????
, ∴tan30°=
????
9
, ∴
????
9
=
3
3
, ∴AF=3
3
m, 在Rt△BCF中, ∵∠BCF=45°, ∴BF=CF=9m, ∴AB=AF+BF=3
3
+9(m).
26.【答案】解:根据题意画出图形, / 根据题意可知AB=60千米,∠BAF=30° 过B作BD⊥AF于点D,作BE=BF=50千米,分别交AF于点E、F ∵ BD⊥AF,AB=60千米,∠BAF=30° ∴ 风暴离B城市的最近距离为BD=AB×sin30°=30千米, ∵ BD<50千米 ∴ 沿海城市B会受到这次风暴的影响 ∵ BE=BF=50千米 ∴ 沿海城市B受影响时风暴所走的路程为线段EF ∵ BE=BF=50千米,BD=30千米,BD⊥AF ∴ DF=DE=
50
2
?
30
2
=40 ∴ EF=2DF=80千米 ∵ 风暴速度为每小时20千米 ∴ 受影响时间=
80
20
=4小时 ∴沿海城市B会受到这次风暴的影响,受影响的时间为4小时。
27.【答案】解:过点D作DE⊥AB于点E,得矩形DEBC, 设塔高AB=xm,则AE=(x﹣10)m, 在Rt△ADE中,∠ADE=30°, 则DE=
3
(x﹣10)米, 在Rt△ABC中,∠ACB=45°, 则BC=AB=x, 由题意得,
3
(x﹣10)=x, 解得:x=15+5
3
≈23.7.即AB≈23.7米. 答:塔的高度约为23.7米. /
28.【答案】解:需要拆除,理由为: ∵CB⊥AB , ∠CAB=45°, ∴△ABC为等腰直角三角形, ∴AB=BC=10米, 在Rt△BCD中,新坡面DC的坡度为i= /:3,即∠CDB=30°, ∴DC=2BC=20米,BD= /米, ∴AD=BD-AB=(10 /-10)米≈7.32米, ∵3+7.32=10.32>10, ∴需要拆除 .
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
